Hostname: page-component-7dd5485656-wxk4p Total loading time: 0 Render date: 2025-10-31T22:10:42.629Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectral analysis of the transition to turbulence from a dipole in stratified fluid

Published online by Cambridge University Press:  11 October 2012

Pierre Augier ,
Jean-Marc Chomaz  and
Paul Billant
Pierre Augier
Affiliation:
LadHyX, CNRS, Ecole Polytechnique, 91128 Palaiseau CEDEX, France
Jean-Marc Chomaz
Affiliation:
LadHyX, CNRS, Ecole Polytechnique, 91128 Palaiseau CEDEX, France
Paul Billant
Affiliation:
LadHyX, CNRS, Ecole Polytechnique, 91128 Palaiseau CEDEX, France
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the spectral properties of the turbulence generated during the nonlinear evolution of a Lamb–Chaplygin dipole in a stratified fluid for a high Reynolds number 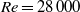$Re= 28\hspace{0.167em} 000$ and a wide range of horizontal Froude number 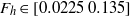${F}_{h} \in [0. 0225~0. 135] $ and buoyancy Reynolds number 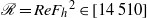$\mathscr{R}= Re{{F}_{h} }^{2} \in [14~510] $ . The numerical simulations use a weak hyperviscosity and are therefore almost direct numerical simulations (DNS). After the nonlinear development of the zigzag instability, both shear and gravitational instabilities develop and lead to a transition to small scales. A spectral analysis shows that this transition is dominated by two kinds of transfer: first, the shear instability induces a direct non-local transfer toward horizontal wavelengths of the order of the buoyancy scale 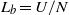${L}_{b} = U/ N$ , where 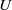$U$ is the characteristic horizontal velocity of the dipole and 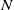$N$ the Brunt–Väisälä frequency; second, the destabilization of the Kelvin–Helmholtz billows and the gravitational instability lead to small-scale weakly stratified turbulence. The horizontal spectrum of kinetic energy exhibits a 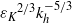${{\varepsilon }_{K} }^{2/ 3} { k}_{h}^{\ensuremath{-} 5/ 3} $ power law (where 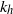${k}_{h} $ is the horizontal wavenumber and 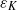${\varepsilon }_{K} $ is the dissipation rate of kinetic energy) from 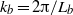${k}_{b} = 2\lrm{\pi} / {L}_{b} $ to the dissipative scales, with an energy deficit between the integral scale and ${k}_{b} $ and an excess around 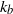${k}_{b} $ . The vertical spectrum of kinetic energy can be expressed as 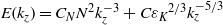$E({k}_{z} )= {C}_{N} {N}^{2} { k}_{z}^{\ensuremath{-} 3} + C{{\varepsilon }_{K} }^{2/ 3} { k}_{z}^{\ensuremath{-} 5/ 3} $ where ${C}_{N} $ and $C$ are two constants of order unity and 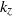${k}_{z} $ is the vertical wavenumber. It is therefore very steep near the buoyancy scale with an 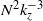${N}^{2} { k}_{z}^{\ensuremath{-} 3} $ shape and approaches the 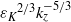${{\varepsilon }_{K} }^{2/ 3} { k}_{z}^{\ensuremath{-} 5/ 3} $ spectrum for ${k}_{z} \gt {k}_{o} $ , 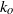${k}_{o} $ being the Ozmidov wavenumber, which is the cross-over between the two scaling laws. A decomposition of the vertical spectra depending on the horizontal wavenumber value shows that the 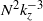${N}^{2} { k}_{z}^{\ensuremath{-} 3} $ spectrum is associated with large horizontal scales 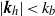$\vert {\mathbi{k}}_{h} \vert \lt {k}_{b} $ and the 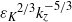${{\varepsilon }_{K} }^{2/ 3} { k}_{z}^{\ensuremath{-} 5/ 3} $ spectrum with the scales 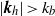$\vert {\mathbi{k}}_{h} \vert \gt {k}_{b} $ .

JFM classification

Instability: Instability Geophysical and Geological Flows: Stratified flows Instability: Transition to turbulence

Information

Type
Papers
Information
Journal of Fluid Mechanics , Volume 713 , 25 December 2012 , pp. 86 - 108
Copyright
©2012 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Augier, P. 2011 Turbulence in strongly stratified fluids: cascade processes. PhD thesis, LadHyX, Ecole Polytechnique..Google Scholar
Augier, P. & Billant, P. 2011 Onset of secondary instabilities on the zigzag instability in stratified fluids. J. Fluid Mech. 662, 120–131.Google Scholar
Billant, P. 2010 Zigzag instability of vortex pairs in stratified and rotating fluids. Part 1. General stability equations. J. Fluid Mech. 660, 354–395.CrossRefGoogle Scholar
Billant, P. & Chomaz, J.-M. 2000a Experimental evidence for a new instability of a vertical columnar vortex pair in a strongly stratified fluid. J. Fluid Mech. 418, 167–188.Google Scholar
Billant, P. & Chomaz, J.-M. 2000b Theoretical analysis of the zigzag instability of a vertical columnar vortex pair in a strongly stratified fluid. J. Fluid Mech. 419, 29–63.CrossRefGoogle Scholar
Billant, P. & Chomaz, J.-M. 2000c Three-dimensional stability of a vertical columnar vortex pair in a stratified fluid. J. Fluid Mech. 419, 65–91.CrossRefGoogle Scholar
Billant, P. & Chomaz, J.-M. 2001 Self-similarity of strongly stratified inviscid flows. Phys. Fluids 13, 1645–1651.Google Scholar
Billant, P., Deloncle, A., Chomaz, J.-M. & Otheguy, P. 2010 Zigzag instability of vortex pairs in stratified and rotating fluids. Part 2. Analytical and numerical analyses. J. Fluid Mech. 660, 396–429.CrossRefGoogle Scholar
Brethouwer, G., Billant, P., Lindborg, E. & Chomaz, J.-M. 2007 Scaling analysis and simulation of strongly stratified turbulent flows. J. Fluid Mech. 585, 343–368.CrossRefGoogle Scholar
de Bruyn Kops, S. M. & Riley, J. J. 1998 Direct numerical simulation of laboratory experiments in isotropic turbulence. Phys. Fluids 10, 2125–2127.Google Scholar
Cambon, C. 2001 Turbulence and vortex structures in rotating and stratified flows. Eur. J. Mech. (B/Fluids 20, 489–510.Google Scholar
Craya, A. D. 1958 Contribution à l’analyse de la turbulence associée à des vitesses moyennes. Ministére de l’air, France PST 345.Google Scholar
Deloncle, A., Billant, P. & Chomaz, J.-M. 2008 Nonlinear evolution of the zigzag instability in stratified fluids: a shortcut on the route to dissipation. J. Fluid Mech. 599, 229–238.Google Scholar
Dewan, E. 1997 Saturated-cascade similitude theory of gravity wave spectra. J. Geophys. Res. 102 (D25), 29799–29817.Google Scholar
Garrett, C. & Munk, W. 1979 Internal waves in the ocean. Annu. Rev. Fluid Mech. 11, 339–369.CrossRefGoogle Scholar
Godeferd, F. S. & Staquet, C. 2003 Statistical modelling and direct numerical simulations of decaying stably stratified turbulence. Part 2. Large-scale and small-scale anisotropy. J. Fluid Mech. 486, 115–159.CrossRefGoogle Scholar
Gotoh, T., Fukayama, D. & Nakano, T. 2002 Velocity field statistics in homogeneous steady turbulence obtained using a high-resolution direct numerical simulation. Phys. Fluids 14 (3), 1065–1081.Google Scholar
Gregg, M. C. 1987 Diapycnal mixing in the thermocline – a review. J. Geophys. Res. 92 (C5), 5249–5286.Google Scholar
Hebert, D. A. & de Bruyn Kops, S. M. 2006 Predicting turbulence in flows with strong stable stratification. Phys. Fluids 18, 066602.Google Scholar
Herring, J. R. 1974 Approach of axisymmetric turbulence to isotropy. Phys. Fluids 17, 859–872.CrossRefGoogle Scholar
Holloway, G. 1983 A conjecture relating oceanic internal waves and small-scale processes. Atmos.-Ocean 21 (1), 107–122.Google Scholar
Kolmogorov, A. N. 1941 The local structure of turbulence in incomressible viscous fluids for very large Reynolds numbers. C. R. Acad. Sci. (USSR) 30, 301–305.Google Scholar
Koshyk, J. N. & Hamilton, K. 2001 The horizontal kinetic energy spectrum and spectral budget simulated by a high-resolution troposphere–stratosphere–mesosphere GCM. J. Atmos. Sci. 58 (4), 329–348.2.0.CO;2>CrossRefGoogle Scholar
Laval, J. P., McWilliams, J. C. & Dubrulle, B. 2003 Forced stratified turbulence: successive transitions with Reynolds number. Phys. Rev. E 68 (3, Part 2), 036308.CrossRefGoogle ScholarPubMed
Lindborg, E. 2002 Strongly stratified turbulence: a special type of motion. In Advances in Turbulence IX, Proceedings of the Ninth European Turbulence Conference, Southampton.Google Scholar
Lindborg, E. 2006 The energy cascade in a strongly stratified fluid. J. Fluid Mech. 550, 207–242.Google Scholar
Lindborg, E. & Brethouwer, G. 2007 Stratified turbulence forced in rotational and divergent modes. J. Fluid Mech. 586, 83–108.Google Scholar
Lumley, J. L. 1964 The spectrum of nearly inertial turbulence in a stably stratified fluid. J. Atmos. Sci. 21 (1), 99–102.2.0.CO;2>CrossRefGoogle Scholar
Lundbladh, A., Berlin, S., Skote, M., Hildings, C., Choi, J., Kim, J. & Henningson, D. S. 1999 An efficient spectral method for simulation of incompressible flow over a flat plate. Trita-mek. Tech. Rep. 11, 265–335.Google Scholar
Monin, A. S. & Yaglom, A. M. 1975 Statistical Fluid Mechanics, vol. 2. MIT.Google Scholar
Nastrom, G. D. & Gage, K. S. 1985 A climatology of atmospheric wavenumber spectra of wind and temperature observed by commercial aircraft. J. Atmos. Sci. 42, 950–960.Google Scholar
Otheguy, P., Chomaz, J.-M. & Billant, P. 2006 Elliptic and zigzag instabilities on co-rotating vertical vortices in a stratified fluid. J. Fluid Mech. 553, 253–272.Google Scholar
Ozmidov, R. V. 1965 On the turbulent exchange in a stably stratified ocean. Izv. Akad. Sci. USSR, Atmos. Ocean. Phys. 1, 493–497.Google Scholar
Riley, J. J. & de Bruyn Kops, S. M. 2003 Dynamics of turbulence strongly influenced by buoyancy. Phys. Fluids 15 (7), 2047–2059.CrossRefGoogle Scholar
Riley, J. J. & Lindborg, E. 2008 Stratified turbulence: a possible interpretation of some geophysical turbulence measurements. J. Atmos. Sci. 65, 2416–2424.Google Scholar
Smith, L. M. & Waleffe, F. 2002 Generation of slow large scales in forced rotating stratified turbulence. J. Fluid Mech. 451, 145–168.Google Scholar
Sreenivasan, K. R. 1995 On the universality of the Kolmogorov constant. Phys. Fluids 7 (11), 2778–2784.Google Scholar
Staquet, C. & Riley, J. J. 1989 On the velocity field associated with potential vorticity. Dyn. Atmos. Oceans 14, 93–123.Google Scholar
Waite, M. L. 2011 Stratified turbulence at the buoyancy scale. Phys. Fluids 23 (6), 066602.CrossRefGoogle Scholar
Waite, M. L. & Bartello, P. 2004 Stratified turbulence dominated by vortical motion. J. Fluid Mech. 517, 281–308.Google Scholar
Waite, M. L. & Smolarkiewicz, P. K. 2008 Instability and breakdown of a vertical vortex pair in a strongly stratified fluid. J. Fluid Mech. 606, 239–273.Google Scholar