Article contents
Spectral evolution of weakly nonlinear random waves: kinetic description versus direct numerical simulations
Published online by Cambridge University Press: 12 April 2018
Abstract
Kinetic equations are widely used in many branches of science to describe the evolution of random wave spectra. To examine the validity of these equations, we study numerically the long-term evolution of water wave spectra without wind input using three different models. The first model is the classical kinetic (Hasselmann) equation (KE). The second model is the generalised kinetic equation (gKE), derived employing the same statistical closure as the KE but without the assumption of quasistationarity. The third model, which we refer to as the DNS-ZE, is a direct numerical simulation algorithm based on the Zakharov integrodifferential equation, which plays the role of the primitive equation for a weakly nonlinear wave field. It does not employ any statistical assumptions. We perform a comparison of the spectral evolution of the same initial distributions without forcing, with/without a statistical closure and with/without the quasistationarity assumption. For the initial conditions, we choose two narrow-banded spectra with the same frequency distribution and different degrees of directionality. The short-term evolution (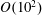 $O(10^{2})$ wave periods) of both spectra has been previously thoroughly studied experimentally and numerically using a variety of approaches. Our DNS-ZE results are validated both with existing short-term DNS by other methods and with available laboratory observations of higher-order moment (kurtosis) evolution. All three models demonstrate very close evolution of integral characteristics of the spectra, approaching with time the theoretical asymptotes of the self-similar stage of evolution. Both kinetic equations give almost identical spectral evolution, unless the spectrum is initially too narrow in angle. However, there are major differences between the DNS-ZE and gKE/KE predictions. First, the rate of angular broadening of initially narrow angular distributions is much larger for the gKE and KE than for the DNS-ZE, although the angular width does appear to tend to the same universal value at large times. Second, the shapes of the frequency spectra differ substantially (even when the nonlinearity is decreased), the DNS-ZE spectra being wider than the KE/gKE ones and having much lower spectral peaks. Third, the maximal rates of change of the spectra obtained with the DNS-ZE scale as the fourth power of nonlinearity, which corresponds to the dynamical time scale of evolution, rather than the sixth power of nonlinearity typical of the kinetic time scale exhibited by the KE. The gKE predictions fall in between. While the long-term DNS show excellent agreement with the KE predictions for integral characteristics of evolving wave spectra, the striking systematic discrepancies for a number of specific spectral characteristics call for revision of the fundamentals of the wave kinetic description.
$O(10^{2})$ wave periods) of both spectra has been previously thoroughly studied experimentally and numerically using a variety of approaches. Our DNS-ZE results are validated both with existing short-term DNS by other methods and with available laboratory observations of higher-order moment (kurtosis) evolution. All three models demonstrate very close evolution of integral characteristics of the spectra, approaching with time the theoretical asymptotes of the self-similar stage of evolution. Both kinetic equations give almost identical spectral evolution, unless the spectrum is initially too narrow in angle. However, there are major differences between the DNS-ZE and gKE/KE predictions. First, the rate of angular broadening of initially narrow angular distributions is much larger for the gKE and KE than for the DNS-ZE, although the angular width does appear to tend to the same universal value at large times. Second, the shapes of the frequency spectra differ substantially (even when the nonlinearity is decreased), the DNS-ZE spectra being wider than the KE/gKE ones and having much lower spectral peaks. Third, the maximal rates of change of the spectra obtained with the DNS-ZE scale as the fourth power of nonlinearity, which corresponds to the dynamical time scale of evolution, rather than the sixth power of nonlinearity typical of the kinetic time scale exhibited by the KE. The gKE predictions fall in between. While the long-term DNS show excellent agreement with the KE predictions for integral characteristics of evolving wave spectra, the striking systematic discrepancies for a number of specific spectral characteristics call for revision of the fundamentals of the wave kinetic description.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 28
- Cited by

