Hostname: page-component-5b777bbd6c-v47t2 Total loading time: 0 Render date: 2025-06-22T04:46:27.709Z Has data issue: false hasContentIssue false
  • English
  • Français

Speed and structure of turbulent fronts in pipe flow

Published online by Cambridge University Press:  27 January 2017

Baofang Song ,
Dwight Barkley ,
Björn Hof  and
Marc Avila Open the ORCID record for Marc Avila [Opens in a new window]
Baofang Song*
Affiliation:
Center of Applied Space Technology and Microgravity, University of Bremen, 28359 Bremen, Germany Institute of Fluid Mechanics, Friedrich-Alexander-Universität Erlangen-Nürnberg, 91058 Erlangen, Germany
Dwight Barkley
Affiliation:
Mathematics Institute, University of Warwick, Coventry CV4 7AL, UK
Björn Hof
Affiliation:
Institute of Science and Technology Austria, 3400 Klosterneuburg, Austria
Marc Avila
Affiliation:
Center of Applied Space Technology and Microgravity, University of Bremen, 28359 Bremen, Germany Institute of Fluid Mechanics, Friedrich-Alexander-Universität Erlangen-Nürnberg, 91058 Erlangen, Germany
*
†Email address for correspondence: baofang.song@zarm.uni-bremen.de
Get access Rights & Permissions [Opens in a new window]

Abstract

Using extensive direct numerical simulations, the dynamics of laminar–turbulent fronts in pipe flow is investigated for Reynolds numbers between 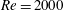$Re=2000$ and 5500. We here investigate the physical distinction between the fronts of weak and strong slugs both by analysing the turbulent kinetic energy budget and by comparing the downstream front motion to the advection speed of bulk turbulent structures. Our study shows that weak downstream fronts travel slower than turbulent structures in the bulk and correspond to decaying turbulence at the front. At 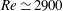$Re\simeq 2900$ the downstream front speed becomes faster than the advection speed, marking the onset of strong fronts. In contrast to weak fronts, turbulent eddies are generated at strong fronts by feeding on the downstream laminar flow. Our study also suggests that temporal fluctuations of production and dissipation at the downstream laminar–turbulent front drive the dynamical switches between the two types of front observed up to 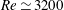$Re\simeq 3200$.

JFM classification

Instability: Transition to turbulence Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 813 , 25 February 2017 , pp. 1045 - 1059
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Avila, K., Moxey, D., De Lozar, A., Avila, M., Barkley, D. & Hof, B. 2011 The onset of turbulence in pipe flow. Science 333, 192–196.CrossRefGoogle ScholarPubMed
Barkley, D. 2011 Simplifying the complexity of pipe flow. Phys. Rev. E 84, 016309.CrossRefGoogle ScholarPubMed
Barkley, D. 2016 Theoretical perspective on the route to turbulence in a pipe. J. Fluid Mech. 803, P1.Google Scholar
Barkley, D., Song, B., Mukund, V., Lemoult, G., Avila, M. & Hof, B. 2015 The rise of fully turbulent flow. Nature 526, 550–553.CrossRefGoogle ScholarPubMed
Barkley, D. & Tuckerman, L. S. 2007 Mean flow of turbulent-laminar patterns in plane Couette flow. J. Fluid Mech. 576, 109–137.Google Scholar
Darbyshire, A. G. & Mullin, T. 1995 Transition to turbulence in constant-mass-flux pipe flow. J. Fluid Mech. 289, 83–114.Google Scholar
Del Álamo, J. C. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.CrossRefGoogle Scholar
van Doorne, C. W. H. & Westerweel, J. 2009 The flow structure of a puff. Phil. Trans. R. Soc. Lond. A 367, 489–507.Google Scholar
Duguet, Y. & Schlatter, P. 2013 Oblique laminar-turbulent interfaces in plane shear flows. Phys. Rev. Lett. 110, 034502.CrossRefGoogle ScholarPubMed
Duguet, Y., Willis, A. P. & Kerswell, R. R. 2010 Slug genesis in cylindrical pipe flow. J. Fluid Mech. 663, 180–208.Google Scholar
Durst, F. & Ünsal, B. 2006 Forced laminar to turbulent transition in pipe flows. J. Fluid Mech. 560, 449–464.Google Scholar
Han, G., Tumin, A. & Wygnanski, I. 2000 Laminar-turbulent transition in Poiseuille pipe flow subjected to periodic perturbation emanating from the wall. Part 2. Late stage of transition. J. Fluid Mech. 419, 1–27.Google Scholar
Hof, B., De Lozar, A., Avila, M., Tu, X. & Schneider, T. M. 2010 Eliminating turbulence in spatially intermittent flows. Science 327, 1491–1494.Google Scholar
Hof, B., Juel, A. & Mullin, T. 2003 Scaling of the turbulence transition threshold in a pipe. Phys. Rev. Lett. 91, 244502.CrossRefGoogle Scholar
Holzner, M., Song, B., Avila, M. & Hof, B. 2013 Lagrangian approach to laminar-turbulent interfaces. J. Fluid Mech. 723, 140–162.Google Scholar
Kim, J. & Hussain, F. 1993 Propagation velocity of perturbations in turbulent channel flow. Phys. Fluids A 5, 695–706.Google Scholar
Kreilos, T., Zammert, S. & Eckhardt, B. 2014 Comoving frames and symmetry-related motions in parallel shear flows. J. Fluid Mech. 751, 685–697.CrossRefGoogle Scholar
Lindgren, E. R. 1969 Propagation velocity of turbulent slugs and streaks in transition pipe flow. Phys. Fluids 12, 418.Google Scholar
Mellibovsky, F. & Meseguer, A. 2007 Pipe flow transition threshold following localized impulsive perturbations. Phys. Fluids 19, 044102.Google Scholar
Mellibovsky, F., Meseguer, A., Schneider, T. M. & Eckhardt, B. 2009 Transition in localized pipe flow turbulence. Phys. Rev. Lett. 103, 054502.CrossRefGoogle ScholarPubMed
Nishi, M., Ünsal, B., Durst, F. & Biswas, G. 2008 Laminar-to-turbulent transition of pipe flows through puffs and slugs. J. Fluid Mech. 614, 425–446.Google Scholar
Pei, J., Chen, J., She, Z.-S. & Hussain, F. 2012 Model for propagation speed in turbulent channel flows. Phys. Rev. E 86, 046307.CrossRefGoogle ScholarPubMed
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Reuter, J. & Rempfer, D. 2004 Analysis of pipe flow transition. Part I. Direct numerical simulation. Theor. Comput. Fluid Dyn. 17, 273–292.Google Scholar
Rotta, J. 1956 Experimenteller beitrag zur entstehung turbulenter strömung im rohr. Ing.-Arch. 24, 258–282.Google Scholar
Sreenivasan, K. R. & Ramshankar, R. 1986 Transition intermittency in open flows, and intermittency routes to chaos. Physica 23D, 246–258.Google Scholar
Willis, A. P. & Kerswell, R. R. 2009 Turbulent dynamics of pipe flow captured in a reduced model: puff relaminarisation and localised ‘edge’ states. J. Fluid Mech. 619, 213–233.Google Scholar
Wygnanski, I. J. & Champagne, F. H. 1973 On transition in a pipe. Part 1. The origin of puffs and slugs and the flow in a turbulent slug. J. Fluid Mech. 59, 281–335.Google Scholar
Wygnanski, I. J., Sokolov, M. & Friedman, D. 1975 On transition in a pipe. Part 2. The equilibrium puff. J. Fluid Mech. 69, 283–304.Google Scholar

Song et al. supplementary movie

Advection of vortices near a weak downstream front at Re = 2600. The flow is from left to right, therefore, the bulk of the slug is on the left and the laminar flow downstream is on the right. Vortices, visualised by using the ?_2 criterion, are shown in the frame of reference co-moving with the front.

Download Song et al. supplementary movie(Video)
Video 9.1 MB

Song et al. supplementary movie

Advection of vortices near a strong downstream front at Re = 5000. The flow is from left to right, therefore, the bulk of the slug is on the left and the laminar flow downstream is on the right. Vortices, visualised by using the ?_2 criterion, are shown in the frame of reference co-moving with the front.

Download Song et al. supplementary movie(Video)
Video 8.1 MB