Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-24T01:23:02.069Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability, intermittency and universal Thorpe length distribution in a laboratory turbulent stratified shear flow

Published online by Cambridge University Press:  21 February 2017

Philippe Odier  and
Robert E. Ecke
Philippe Odier*
Affiliation:
Université de Lyon, ENS de Lyon, Université Claude Bernard Lyon 1, CNRS, Laboratoire de Physique, F-69342 Lyon, France
Robert E. Ecke
Affiliation:
Center for Nonlinear Studies and Condensed Matter & Magnetic Sciences, Los Alamos National Laboratory, Los Alamos, NM 87545, USA
*
†Email address for correspondence: podier@ens-lyon.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Stratified shear flows occur in many geophysical contexts, from oceanic overflows and river estuaries to wind-driven thermocline layers. We explore a turbulent wall-bounded shear flow of lighter miscible fluid into a quiescent fluid of higher density with a range of Richardson numbers 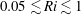$0.05\lesssim Ri\lesssim 1$. In order to find a stability parameter that allows close comparison with linear theory and with idealized experiments and numerics, we investigate different definitions of 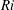$Ri$. We find that a gradient Richardson number defined on fluid interface sections where there is no overturning at or adjacent to the maximum density gradient position provides an excellent stability parameter, which captures the Miles–Howard linear stability criterion. For small $Ri$ the flow exhibits robust Kelvin–Helmholtz instability, whereas for larger 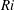$Ri$ interfacial overturning is more intermittent with less frequent Kelvin–Helmholtz events and emerging Holmboe wave instability consistent with a thicker velocity layer compared with the density layer. We compute the perturbed fraction of interface as a quantitative measure of the flow intermittency, which is approximately 1 for the smallest 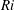$Ri$ but decreases rapidly as 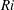$Ri$ increases, consistent with linear theory. For the perturbed regions, we use the Thorpe scale to characterize the overturning properties of these flows. The probability distribution of the non-zero Thorpe length yields a universal exponential form, suggesting that much of the overturning results from increasingly intermittent Kelvin–Helmholtz instability events. The distribution of turbulent kinetic energy, conditioned on the intermittency fraction, has a similar form, suggesting an explanation for the universal scaling collapse of the Thorpe length distribution.

JFM classification

Boundary Layers: Free shear layers Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 815 , 25 March 2017 , pp. 243 - 256
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexakis, A. 2005 On Holmboe’s instability for smooth shear and density profiles. Phys. Fluids 17, 084103.CrossRefGoogle Scholar
Baines, P. G. 2005 Mixing regimes for the flow of dense fluid down slopes into stratified environments. J. Fluid Mech. 538, 245–267.Google Scholar
Baines, P. G. & Mitsudera, H. 1994 On the mechanism of shear-flow instabilities. J. Fluid Mech. 276, 327–342.CrossRefGoogle Scholar
Browand, F. K. & Winant, C. D. 1973 Laboratory observations of shear-layer instability in a stratified fluid. Boundary-Layer Meteorol. 5, 67–77.CrossRefGoogle Scholar
Carpenter, J. R., Tedford, E. W., Heifetz, E. & Lawrence, G. A. 2011 Instability in stratified shear flow: review of physical interpretation based on interacting waves. Appl. Mech. Rev. 64, 060801.Google Scholar
Carpenter, J. R., Tedford, E. W., Rahmani, M. & Lawrence, G. A. 2010 Holmboe wave fields in simulation and experiment. J. Fluid Mech. 648, 205–223.CrossRefGoogle Scholar
Caulfield, C. P. & Peltier, W. R. 2000 The anatomy of the mixing transition in homogeneous and stratified free shear layers. J. Fluid Mech. 413, 1–47.CrossRefGoogle Scholar
Cenedese, C. & Adduce, C. 2008 Mixing in a density-driven current flowing down a slope in a rotating fluid. J. Fluid Mech. 604, 369–388.CrossRefGoogle Scholar
Dillon, T. M. 1982 Vertical overturns – a comparison of Thorpe and Ozmidov length scales. J. Geophys. Res. – Oceans 87 (NC12), 9601–9613.Google Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Fernando, H. J. S. 1991 Turbulent mixing in stratified fluids. Annu. Rev. Fluid Mech. 23, 455–493.Google Scholar
Hazel, P. 1972 Numerical studies of the stability of inviscid stratified shear layers. J. Fluid Mech. 51, 39–61.Google Scholar
Hogg, A. McC. & Ivey, G. N. 2003 The Kelvin–Helmholtz to Holmboe instability transition in stratified exchange flow. J. Fluid Mech. 477, 339–362.CrossRefGoogle Scholar
Holmboe, J. 1962 On the behaviour of symmetric waves in stratified shear layers. Geofysiske Publikasjoner 24, 67–113.Google Scholar
Howard, L. N. 1961 Note on a paper by John W. Miles. J. Fluid Mech. 10, 509–512.CrossRefGoogle Scholar
Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22, 473–537.Google Scholar
Imberger, J. & Ivey, G. N. 1991 On the nature of turbulence in a stratified fluids. Part II. Application to lakes. J. Phys. Oceanogr. 21, 659–680.Google Scholar
Ivey, G. N., Winters, K. B. & Koseff, J. R. 2008 Density stratification, turbulence, but how much mixing? Annu. Rev. Fluid Mech. 401, 169–184.Google Scholar
Lawrence, G. A., Browand, F. K. & Redekopp, L. G. 1991 The stability of a sheared density interface. Phys. Fluids A 3 (10), 2360–2370.Google Scholar
Mellor, G. L. & Durbin, P. A. 1975 The structure and dynamics of the ocean surface mixed layer. J. Phys. Oceanogr. 5, 718–728.Google Scholar
Miles, J. W. 1961 On the stability of heterogeneous shear flows. J. Fluid Mech. 10, 496–508.Google Scholar
Odier, P., Chen, J. & Ecke, R. E. 2014 Entrainment and mixing in a laboratory model of oceanic overflow. J. Fluid Mech. 746, 498–535.CrossRefGoogle Scholar
Odier, P., Chen, J., Rivera, M. K. & Ecke, R. E. 2009 Fluid mixing in stratified gravity currents: the Prandtl mixing length. Phys. Rev. Lett. 102 (13), 134504.Google Scholar
Ortiz, S., Chomaz, J. M. & Loiseleux, T. 2002 Spatial Holmboe instability. Phys. Fluids 14, 2585–2597.CrossRefGoogle Scholar
Peltier, W. R. & Caulfield, C. P. 2003 Mixing efficiency in stratified shear flows. Annu. Rev. Fluid Mech. 35, 135–167.Google Scholar
Price, J., Baringer, M., Lueck, R., Johnson, G. & others 1993 Mediterranean outflow mixing and dynamics. Science 259, 1278–1282.CrossRefGoogle ScholarPubMed
Smyth, W. D., Moum, J. N. & Caldwell, D. R. 2001 The efficiency of mixing in turbulent patches: inferences from direct simulations and microstructure observations. J. Phys. Oceanogr. 31, 1969–1992.Google Scholar
Smyth, W. D. & Peltier, W. R. 1989 The transition between Kelvin–Helmholtz and Holmboe instability: an investigation of the overreflection hypothesis. J. Atmos. Sci. 46, 3698–3720.2.0.CO;2>CrossRefGoogle Scholar
Tanino, Y., Moisy, F. & Hulin, J. P. 2012 Laminar–turbulent cycles in inclined lock-exchange flows. Phys. Rev. E 85, 066308.Google Scholar
Tedford, E. W., Carpenter, J. R., Pawlowicz, R., Pieters, R. & Lawrence, G. A. 2009 Observation and analysis of shear instability in the Fraser River estuary. J. Geophys. Res. Oceans 114, C11006.Google Scholar
Thorpe, S. A. 1977 Turbulence and mixing in a Scottish loch. Phil. Trans. R. Soc. Lond. A 286 (1334), 125–181.Google Scholar
Thorpe, S. A. 2005 The Turbulent Ocean. Cambridge University Press.Google Scholar
Thorpe, S. A. 2009 Marginal instability? J. Phys. Oceanogr. 39 (Sep), 2373–2381.Google Scholar
Winters, K. B., Lombard, P. N., Riley, J. J. & D’Asaro, E. A. 1995 Available potential energy and mixing in density-stratified fluids. J. Fluid Mech. 289, 115–128.Google Scholar
Yonemitsu, N., Swaters, G. E., Rajaratnam, N. & Lawrence, G. A. 1996 Shear instabilities in arrested salt-wedge flows. Dyn. Atmos. Oceans 24 (1–4), 173–182; 4th International Symposium on Stratified Flows, Univ. Joseph Fourier, Grenoble, France, June 29–July 2, 1994.Google Scholar