Article contents
Stability of a temporally evolving natural convection boundary layer on an isothermal wall
Published online by Cambridge University Press: 02 September 2019
Abstract
The stability properties of a natural convection boundary layer adjacent to an isothermally heated vertical wall, with Prandtl number 0.71, are numerically investigated in the configuration of a temporally evolving parallel flow. The instantaneous linear stability of the flow is first investigated by solving the eigenvalue problem with a quasi-steady assumption, whereby the unsteady base flow is frozen in time. Temporal responses of the discrete perturbation modes are numerically obtained by solving the two-dimensional linearized disturbance equations using a‘frozen’ base flow as an initial-value problem at various 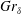 $Gr_{\unicode[STIX]{x1D6FF}}$, where
$Gr_{\unicode[STIX]{x1D6FF}}$, where 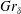 $Gr_{\unicode[STIX]{x1D6FF}}$ is the Grashof number based on the velocity integral boundary layer thickness
$Gr_{\unicode[STIX]{x1D6FF}}$ is the Grashof number based on the velocity integral boundary layer thickness 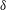 $\unicode[STIX]{x1D6FF}$. The resultant amplification rates of the discrete modes are compared with the quasi-steady eigenvalue analysis, and both two-dimensional and three-dimensional direct numerical simulations (DNS) of the temporally evolving flow. The amplification rate predicted by the linear theory compares well with the result of direct numerical simulation up to a transition point. The extent of the linear regime where the perturbations linearly interact with the base flow is thus identified. The value of the transition
$\unicode[STIX]{x1D6FF}$. The resultant amplification rates of the discrete modes are compared with the quasi-steady eigenvalue analysis, and both two-dimensional and three-dimensional direct numerical simulations (DNS) of the temporally evolving flow. The amplification rate predicted by the linear theory compares well with the result of direct numerical simulation up to a transition point. The extent of the linear regime where the perturbations linearly interact with the base flow is thus identified. The value of the transition 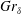 $Gr_{\unicode[STIX]{x1D6FF}}$, according to the three-dimensional DNS results, is dependent on the initial perturbation amplitude. Beyond the transition point, the DNS results diverge from the linear stability predictions as nonlinear mechanisms become important.
$Gr_{\unicode[STIX]{x1D6FF}}$, according to the three-dimensional DNS results, is dependent on the initial perturbation amplitude. Beyond the transition point, the DNS results diverge from the linear stability predictions as nonlinear mechanisms become important.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 16
- Cited by

