Article contents
Stability of columnar convection in a porous medium
Published online by Cambridge University Press: 22 November 2013
Abstract
Convection in a porous medium at high Rayleigh number 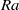 $\mathit{Ra}$ exhibits a striking quasisteady columnar structure with a well-defined and
$\mathit{Ra}$ exhibits a striking quasisteady columnar structure with a well-defined and 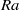 $\mathit{Ra}$ -dependent horizontal scale. The mechanism that controls this scale is not currently understood. Motivated by this problem, the stability of a density-driven ‘heat-exchanger’ flow in a porous medium is investigated. The dimensionless flow comprises interleaving columns of horizontal wavenumber
$\mathit{Ra}$ -dependent horizontal scale. The mechanism that controls this scale is not currently understood. Motivated by this problem, the stability of a density-driven ‘heat-exchanger’ flow in a porous medium is investigated. The dimensionless flow comprises interleaving columns of horizontal wavenumber 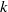 $k$ and amplitude
$k$ and amplitude 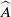 $\widehat{A}$ that are driven by a steady balance between vertical advection of a background linear density stratification and horizontal diffusion between the columns. Stability is governed by the parameter
$\widehat{A}$ that are driven by a steady balance between vertical advection of a background linear density stratification and horizontal diffusion between the columns. Stability is governed by the parameter 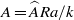 $A= \widehat{A}\mathit{Ra}/ k$ . A Floquet analysis of the linear-stability problem in an unbounded two-dimensional domain shows that the flow is always unstable, and that the marginal-stability curve is independent of
$A= \widehat{A}\mathit{Ra}/ k$ . A Floquet analysis of the linear-stability problem in an unbounded two-dimensional domain shows that the flow is always unstable, and that the marginal-stability curve is independent of 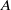 $A$ . The growth rate of the most unstable mode scales with
$A$ . The growth rate of the most unstable mode scales with 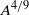 ${A}^{4/ 9} $ for
${A}^{4/ 9} $ for 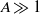 $A\gg 1$ , and the corresponding perturbation takes the form of vertically propagating pulses on the background columns. The physical mechanism behind the instability is investigated by an asymptotic analysis of the linear-stability problem. Direct numerical simulations show that nonlinear evolution of the instability ultimately results in a reduction of the horizontal wavenumber of the background flow. The results of the stability analysis are applied to the columnar flow in a porous Rayleigh–Bénard (Rayleigh–Darcy) cell at high
$A\gg 1$ , and the corresponding perturbation takes the form of vertically propagating pulses on the background columns. The physical mechanism behind the instability is investigated by an asymptotic analysis of the linear-stability problem. Direct numerical simulations show that nonlinear evolution of the instability ultimately results in a reduction of the horizontal wavenumber of the background flow. The results of the stability analysis are applied to the columnar flow in a porous Rayleigh–Bénard (Rayleigh–Darcy) cell at high 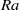 $\mathit{Ra}$ , and a balance of the time scales for growth and propagation suggests that the flow is unstable for horizontal wavenumbers
$\mathit{Ra}$ , and a balance of the time scales for growth and propagation suggests that the flow is unstable for horizontal wavenumbers 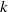 $k$ greater than
$k$ greater than 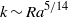 $k\sim {\mathit{Ra}}^{5/ 14} $ as
$k\sim {\mathit{Ra}}^{5/ 14} $ as 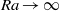 $\mathit{Ra}\rightarrow \infty $ . This stability criterion is consistent with hitherto unexplained numerical measurements of
$\mathit{Ra}\rightarrow \infty $ . This stability criterion is consistent with hitherto unexplained numerical measurements of 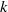 $k$ in a Rayleigh–Darcy cell.
$k$ in a Rayleigh–Darcy cell.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 28
- Cited by

