Article contents
Stirring and scalar transfer by grid-generated turbulence in the presence of a mean scalar gradient
Published online by Cambridge University Press: 23 December 2014
Abstract
The stirring of a passive scalar by grid-generated turbulence in the presence of a mean scalar gradient is studied by direct numerical simulations (DNS) for six different grids: one fractal square grid with three fractal iterations, one fractal square grid with four fractal iterations, one fractal I grid and three different regular grids. Our results can be summarised as follows. (i) For all these grids, the turbulence intensity averaged over time and over a plane parallel to the grid takes its peak value when the streamwise position of this plane is between 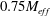 $0.75M_{eff}$ and
$0.75M_{eff}$ and 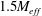 $1.5M_{eff}$ where
$1.5M_{eff}$ where 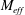 $M_{eff}$ is the effective mesh size introduced by Hurst & Vassilicos (Phys. Fluids, vol. 19, 2007, 035103). (ii) Downstream of the location of this peak, the turbulence intensity averaged in this way is greatly enhanced by the fractal grids relative to the regular grids even though the fractal grids have comparable or even lower blockage ratios. The novelty of this result lies in the fact that it concerns turbulence intensities averaged over lateral planes (as well as time). (iii) The pressure drop is about the same across grids of the same blockage ratio whether fractal or not, but the pressure recovery is longer for the fractal grids. (iv) Even so, the fractal grids enhance turbulent scalar fluxes by up to an order of magnitude in the region downstream of the aforementioned peak and they also greatly enhance the streamwise growth of the fluctuating scalar variance in that region. (v) We demonstrate on a simple planar model problem that the cause of this phenomenon lies in the fractality of the grids. (vi) The turbulence scalar flux coefficient is constant far enough downstream of all the present grids and is significantly dependent on the nature and details of the turbulence-generating grid.
$M_{eff}$ is the effective mesh size introduced by Hurst & Vassilicos (Phys. Fluids, vol. 19, 2007, 035103). (ii) Downstream of the location of this peak, the turbulence intensity averaged in this way is greatly enhanced by the fractal grids relative to the regular grids even though the fractal grids have comparable or even lower blockage ratios. The novelty of this result lies in the fact that it concerns turbulence intensities averaged over lateral planes (as well as time). (iii) The pressure drop is about the same across grids of the same blockage ratio whether fractal or not, but the pressure recovery is longer for the fractal grids. (iv) Even so, the fractal grids enhance turbulent scalar fluxes by up to an order of magnitude in the region downstream of the aforementioned peak and they also greatly enhance the streamwise growth of the fluctuating scalar variance in that region. (v) We demonstrate on a simple planar model problem that the cause of this phenomenon lies in the fractality of the grids. (vi) The turbulence scalar flux coefficient is constant far enough downstream of all the present grids and is significantly dependent on the nature and details of the turbulence-generating grid.
Information
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 30
- Cited by


