Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Cai, Shengze
Mémin, Etienne
Dérian, Pierre
and
Xu, Chao
2018.
Motion estimation under location uncertainty for turbulent fluid flows.
Experiments in Fluids,
Vol. 59,
Issue. 1,
Chapron, B.
Dérian, P.
Mémin, E.
and
Resseguier, V.
2018.
Large‐scale flows under location uncertainty: a consistent stochastic framework.
Quarterly Journal of the Royal Meteorological Society,
Vol. 144,
Issue. 710,
p.
251.
Chandramouli, Pranav
Heitz, Dominique
Laizet, Sylvain
and
Mémin, Etienne
2018.
Coarse large-eddy simulations in a transitional wake flow with flow models under location uncertainty.
Computers & Fluids,
Vol. 168,
Issue. ,
p.
170.
Yang, Yin
and
Mémin, Etienne
2019.
Estimation of physical parameters under location uncertainty using an ensemble2–expectation–maximization algorithm.
Quarterly Journal of the Royal Meteorological Society,
Vol. 145,
Issue. 719,
p.
418.
Cintolesi, Carlo
and
Mémin, Etienne
2020.
Stochastic Modelling of Turbulent Flows for Numerical Simulations.
Fluids,
Vol. 5,
Issue. 3,
p.
108.
Bauer, Werner
Chandramouli, Pranav
Li, Long
and
Mémin, Etienne
2020.
Stochastic representation of mesoscale eddy effects in coarse-resolution barotropic models.
Ocean Modelling,
Vol. 151,
Issue. ,
p.
101646.
Bauer, Werner
Chandramouli, Pranav
Chapron, Bertrand
Li, Long
and
Mémin, Etienne
2020.
Deciphering the Role of Small-Scale Inhomogeneity on Geophysical Flow Structuration: A Stochastic Approach.
Journal of Physical Oceanography,
Vol. 50,
Issue. 4,
p.
983.
de Léon, Aythami Bethencourt
Holm, Darryl D.
Luesink, Erwin
and
Takao, So
2020.
Implications of Kunita–Itô–Wentzell Formula for k-Forms in Stochastic Fluid Dynamics.
Journal of Nonlinear Science,
Vol. 30,
Issue. 4,
p.
1421.
Resseguier, V.
Li, L.
Jouan, G.
Dérian, P.
Mémin, E.
and
Chapron, B.
2021.
New Trends in Ensemble Forecast Strategy: Uncertainty Quantification for Coarse-Grid Computational Fluid Dynamics.
Archives of Computational Methods in Engineering,
Vol. 28,
Issue. 1,
p.
215.
Resseguier, Valentin
Picard, Agustin M.
Memin, Etienne
and
Chapron, Bertrand
2021.
Quantifying Truncation-Related Uncertainties in Unsteady Fluid Dynamics Reduced Order Models.
SIAM/ASA Journal on Uncertainty Quantification,
Vol. 9,
Issue. 3,
p.
1152.
Resseguier, Valentin
Ladvig, Matheus
and
Heitz, Dominique
2022.
Real-time estimation and prediction of unsteady flows using reduced-order models coupled with few measurements.
Journal of Computational Physics,
Vol. 471,
Issue. ,
p.
111631.
Tissot, Gilles
Cavalieri, André V. G.
and
Mémin, Étienne
2023.
Input-output analysis of the stochastic Navier-Stokes equations: Application to turbulent channel flow.
Physical Review Fluids,
Vol. 8,
Issue. 3,
Ross, Molly
and
Bindra, Hitesh
2023.
Development of a subgrid-scale model for Burgers turbulence using statistical mechanics-based methods.
Physics of Fluids,
Vol. 35,
Issue. 12,
Guang, Weilong
Lu, Jiahao
Pan, Jiale
Tao, Ran
Xiao, Ruofu
and
Liu, Weichao
2024.
Study on runaway performance of pump-turbine based on Finite-Time Lyapunov Exponent and Proper Orthogonal Decomposition method.
Journal of Energy Storage,
Vol. 83,
Issue. ,
p.
110759.
Guang, Weilong
Wang, Peng
Zhang, Jinshuai
Yuan, Linjuan
Wang, Yue
Feng, Guang
and
Tao, Ran
2024.
Reduced Order Data-Driven Analysis of Cavitating Flow over Hydrofoil with Machine Learning.
Journal of Marine Science and Engineering,
Vol. 12,
Issue. 1,
p.
148.
Kostelecky, Jonathan
and
Ansorge, Cedrick
2024.
Simulation and scaling analysis of periodic surfaces with small-scale roughness in turbulent Ekman flow.
Journal of Fluid Mechanics,
Vol. 992,
Issue. ,
Diamantakis, Theo
and
Woodfield, James
2025.
Lévy Areas, Wong–Zakai Anomalies in Diffusive Limits of Deterministic Lagrangian Multitime Dynamics.
SIAM Journal on Applied Dynamical Systems,
Vol. 24,
Issue. 1,
p.
836.
Debussche, Arnaud
Mémin, Etienne
and
Moneyron, Antoine
2025.
Stochastic Transport in Upper Ocean Dynamics III.
Vol. 13,
Issue. ,
p.
161.
Tucciarone, Francesco L.
Li, Long
Mémin, Etienne
and
Chandramouli, Pranav
2025.
Derivation and Numerical Assessment of a Stochastic Large–Scale Hydrostatic Primitive Equations Model.
Journal of Advances in Modeling Earth Systems,
Vol. 17,
Issue. 7,
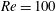 $Re=100$ and
$Re=100$ and 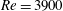 $Re=3900$ . The finite-dimensional models of the wake flows reveal the energy and the anisotropy distributions of the small-scale diffusion modes. These distributions identify critical regions where corrective advection effects, as well as structured energy dissipation effects, take place. In providing rigorously derived subgrid terms, the proposed approach yields accurate and robust temporal reconstruction of the low-dimensional models.
$Re=3900$ . The finite-dimensional models of the wake flows reveal the energy and the anisotropy distributions of the small-scale diffusion modes. These distributions identify critical regions where corrective advection effects, as well as structured energy dissipation effects, take place. In providing rigorously derived subgrid terms, the proposed approach yields accurate and robust temporal reconstruction of the low-dimensional models.

