Article contents
Streaming-potential phenomena in the thin-Debye-layer limit. Part 2. ModeratePéclet numbers
Published online by Cambridge University Press: 03 July 2012
Abstract
Macroscale description of streaming-potential phenomena in the thin-double-layer limit, and in particular the associated electro-viscous forces, has been a matter of long-standing controversy. In part 1 of this work (Yariv, Schnitzer & Frankel, J. Fluid Mech., vol. 685, 2011, pp. 306–334) we identified that the product of the Hartmann (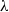 ) and Péclet (
) and Péclet (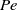 ) numbers is
) numbers is 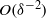 ,
, 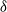 being the dimensionless Debye thickness. This scaling relationship defines a one-family class of limit processes appropriate to the consistent analysis of this singular problem. In that earlier contribution we focused on the generic problems associated with moderate
being the dimensionless Debye thickness. This scaling relationship defines a one-family class of limit processes appropriate to the consistent analysis of this singular problem. In that earlier contribution we focused on the generic problems associated with moderate 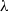 and large
and large 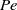 , where the streaming-potential magnitude is comparable to the thermal voltage. Here we consider the companion generic limit of moderate Péclet numbers and large Hartmann numbers, deriving the appropriate macroscale model wherein the Debye-layer physics is represented by effective boundary conditions. Since the induced electric field is asymptotically smaller, calculation of these conditions requires higher asymptotic orders in analysing the Debye-scale transport. Nonetheless, the leading-order electro-viscous forces are of the same
, where the streaming-potential magnitude is comparable to the thermal voltage. Here we consider the companion generic limit of moderate Péclet numbers and large Hartmann numbers, deriving the appropriate macroscale model wherein the Debye-layer physics is represented by effective boundary conditions. Since the induced electric field is asymptotically smaller, calculation of these conditions requires higher asymptotic orders in analysing the Debye-scale transport. Nonetheless, the leading-order electro-viscous forces are of the same 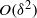 relative magnitude as those previously obtained in the large-
relative magnitude as those previously obtained in the large-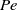 limit. The structure of these forces is different, however, first because the small Maxwell stresses do not contribute at leading order, and second because salt polarization results in a dominant diffuso-osmotic slip. Since the salt distribution is governed by an advection–diffusion equation, this slip gives rise to electro-viscous forces which are nonlinear in the driving flow. The resulting scheme is illustrated by the calculation of the electro-viscous excess drag in the prototype problem of a translating sphere.
limit. The structure of these forces is different, however, first because the small Maxwell stresses do not contribute at leading order, and second because salt polarization results in a dominant diffuso-osmotic slip. Since the salt distribution is governed by an advection–diffusion equation, this slip gives rise to electro-viscous forces which are nonlinear in the driving flow. The resulting scheme is illustrated by the calculation of the electro-viscous excess drag in the prototype problem of a translating sphere.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 16
- Cited by

