Article contents
Streamwise and spanwise slip over a superhydrophobic surface
Published online by Cambridge University Press: 15 May 2019
Abstract
The near-wall turbulent flow over a superhydrophobic surface (SHS) with random texture was studied using three-dimensional Lagrangian particle tracking velocimetry (3D-PTV). The channel was operated at a constant mass flow rate over the SHS and a smooth surface at a Reynolds number of 7000 based on the bulk velocity of 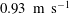 $0.93~\text{m}~\text{s}^{-1}$ and the full channel height. The friction Reynolds number was 217, based on the friction velocity and half channel height. The 3D-PTV processing was based on the shake-the-box algorithm applied to images of fluorescent tracers recorded using four high-speed cameras. The SHS was obtained by spray coating, resulting in a root-mean-square roughness of
$0.93~\text{m}~\text{s}^{-1}$ and the full channel height. The friction Reynolds number was 217, based on the friction velocity and half channel height. The 3D-PTV processing was based on the shake-the-box algorithm applied to images of fluorescent tracers recorded using four high-speed cameras. The SHS was obtained by spray coating, resulting in a root-mean-square roughness of 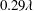 $0.29\unicode[STIX]{x1D706}$ and an average texture width of
$0.29\unicode[STIX]{x1D706}$ and an average texture width of 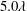 $5.0\unicode[STIX]{x1D706}$, where
$5.0\unicode[STIX]{x1D706}$, where 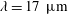 $\unicode[STIX]{x1D706}=17~\unicode[STIX]{x03BC}\text{m}$ is the inner flow scale over the SHS. The 3D-PTV measurements confirmed an isotropic slip with a streamwise slip length of
$\unicode[STIX]{x1D706}=17~\unicode[STIX]{x03BC}\text{m}$ is the inner flow scale over the SHS. The 3D-PTV measurements confirmed an isotropic slip with a streamwise slip length of 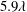 $5.9\unicode[STIX]{x1D706}$ and a spanwise slip length of
$5.9\unicode[STIX]{x1D706}$ and a spanwise slip length of 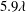 $5.9\unicode[STIX]{x1D706}$. As a result, both the near-wall mean streamwise and spanwise velocity profiles over the SHS were higher than the smooth surface. The streamwise and spanwise slip velocities over the SHS were
$5.9\unicode[STIX]{x1D706}$. As a result, both the near-wall mean streamwise and spanwise velocity profiles over the SHS were higher than the smooth surface. The streamwise and spanwise slip velocities over the SHS were 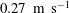 $0.27~\text{m}~\text{s}^{-1}$ and
$0.27~\text{m}~\text{s}^{-1}$ and 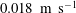 $0.018~\text{m}~\text{s}^{-1}$, respectively. The near-wall Reynolds stresses over the SHS were larger and shifted towards the wall when normalized by the corresponding inner scaling, despite the smaller friction Reynolds number of 180 over the SHS. The near-wall measurement of streamwise velocity showed that the shear-free pattern consists of streamwise-elongated regions with a length of
$0.018~\text{m}~\text{s}^{-1}$, respectively. The near-wall Reynolds stresses over the SHS were larger and shifted towards the wall when normalized by the corresponding inner scaling, despite the smaller friction Reynolds number of 180 over the SHS. The near-wall measurement of streamwise velocity showed that the shear-free pattern consists of streamwise-elongated regions with a length of 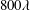 $800\unicode[STIX]{x1D706}$ and a spanwise width of
$800\unicode[STIX]{x1D706}$ and a spanwise width of 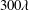 $300\unicode[STIX]{x1D706}$. The plastron dimensions correspond to the mean distance of the largest roughness peaks
$300\unicode[STIX]{x1D706}$. The plastron dimensions correspond to the mean distance of the largest roughness peaks 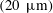 $(20~\unicode[STIX]{x03BC}\text{m})$ obtained from profilometry of the SHS. The drag reduction over the SHS was 30 %–38 % as estimated from pressure measurement and the flow field using the 3D-PTV.
$(20~\unicode[STIX]{x03BC}\text{m})$ obtained from profilometry of the SHS. The drag reduction over the SHS was 30 %–38 % as estimated from pressure measurement and the flow field using the 3D-PTV.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 52
- Cited by

