2. The DNS data

We first introduce the two DNS datasets of homogeneous and isotropic turbulence used in this work. Dataset A is downloaded from snapshot 5 of the ‘Forced isotropic turbulence dataset on $8192^3$ Grid’ dataset (Yeung, Zhai & Sreenivasan Reference Yeung, Zhai and Sreenivasan2015; Yeung, Sreenivasan & Pope Reference Yeung, Sreenivasan and Pope2018) of the Johns Hopkins turbulence database (Li et al. Reference Li, Perlman, Wan, Yang, Meneveau, Burns, Chen, Szalay and Eyink2008), with $8192^3$ grid points and a Taylor-microscale based Reynolds number $R_\lambda = 610$. The spatial resolution is characterized by $k_{max} \eta _K \approx 5.3$, where $k_{max}$ is the largest resolved wavenumber and $\eta _K$ is the Kolmogorov scale. To study the properties of the pressure Hessian conditioned on extreme values of vorticity, we use the ‘GetThreshold’ function of the database and downloaded all data points with $\varOmega \tau _K^2 > 24.98$. Because of the limited storage space, we only keep the points with $24.98 <\varOmega \tau _K^2 <25.02$, $99 <\varOmega \tau _K^2 < 101$ and $\varOmega \tau _K^2 > 196$. Then the statistic for $\varOmega \tau _K^2 = 25$ would be $2.3\times 10^6$, and $2.2 \times 10^6$ for $\varOmega \tau _K^2 = 100$. For comparison, we also downloaded $512^3$ equally spaced data points of the whole snapshot, which would provide information for statistics of unconditional and lower values of vorticity.

Dataset B was obtained by simulating the Navier–Stokes equations using the spectral code described in Pumir (Reference Pumir1994) with $512^3$ grid points and $R_\lambda = 210$, with a lower spatial resolution compared with Dataset A: $k_{max} \eta _K \approx 1.6$. While this resolution is insufficient to reliably capture the statistics of the largest velocity gradients in the flow, we explicitly checked that the probability density function (p.d.f.) of enstrophy, $\varOmega$, coincides with the data shown in figure 2 of Buaria et al. (Reference Buaria, Pumir, Bodenschatz and Yeung2019) at $R_\lambda = 240$, for $\varOmega \tau _K^2 \lesssim 50$. Other tests convinced us that resolution is not an issue over the range of velocity gradient intensity considered here. We saved 21 configurations of the full velocity fields, over a time of the order of ${\sim }10$ eddy turnover times, which we analysed to produce the data shown here.

3. Analysis of the pressure Hessian in regions of very large vorticity

We begin by focusing on the antisymmetric part of the velocity gradient tensor in (1.2), which involves vorticity $\boldsymbol {\omega }$ and thus the enstrophy $\varOmega$:

(3.1)\begin{equation} \frac{1}{2} \frac{{\rm D}\varOmega }{{\rm D}t} = \omega_i {{\mathsf{s}}}_{ij} \omega_j+ \nu \omega_{i} \nabla^2 \omega_{i} , \end{equation}

where ${{\mathsf{s}}}_{ij} \equiv \frac {1}{2}({\mathsf{m}}_{ij} + {\mathsf{m}}_{ji})$ is the rate of strain tensor. Equation (3.1) implies that enstrophy amplification results from a competition between vortex stretching $\omega _i {{\mathsf{s}}}_{ij} \omega _j$ and the viscous diffusion. Notoriously, the pressure Hessian does not explicitly appear in the equations for $\omega _i$ and $\varOmega$. On the other hand, the pressure Hessian ${\partial ^2 p}/{\partial x_i \partial x_j}$ plays an explicit role in the dynamic equation of strain ${{\mathsf{s}}}_{ij}$:

(3.2)\begin{equation} \frac{{\rm D}{{\mathsf{s}}}_{ij} }{{\rm D}t} =- {{\mathsf{s}}}_{ik} {{\mathsf{s}}}_{kj} - \frac{1}{4}\left(\omega_i \omega_j - \omega^2 \delta_{ij}\right) - {{\mathsf{h}}\,}^p_{ij} + \nu \nabla^2 {{\mathsf{s}}}_{ij}, \end{equation}

and, therefore, pressure Hessian will affect the vortex stretching dynamics by acting on strain (Buaria & Pumir Reference Buaria and Pumir2023).

3.1. Heuristic derivation

We start by conditioning the equation of the dynamics of strain, (3.2), on enstrophy $\varOmega$ and taking the conditional average:

(3.3)\begin{equation} \left \langle \frac{{\rm D}{{\mathsf{s}}}_{ij} }{{\rm D}t} | \varOmega \right\rangle + \left \langle {{\mathsf{s}}}_{ik} {{\mathsf{s}}}_{kj} | \varOmega \right\rangle + \left \langle \frac{1}{4}\left(\omega_i \omega_j - \omega^2 \delta_{ij}\right) | \varOmega \right\rangle + \left \langle h^p_{ij} | \varOmega \right\rangle - \left \langle \nu \nabla^2 {{\mathsf{s}}}_{ij} | \varOmega \right\rangle = 0. \end{equation}

Earlier work has shown that vorticity dominates the strain in extreme vorticity regions, in the sense that $\langle \varSigma | \varOmega \rangle \sim \varOmega ^\gamma$, with $\varSigma \equiv 2 {{\mathsf{s}}}_{ij} {{\mathsf{s}}}_{ji}$, and with $\gamma < 1$ when $\varOmega \tau _K^2 \gg 1$ (Buaria et al. Reference Buaria, Pumir, Bodenschatz and Yeung2019; Buaria, Bodenschatz & Pumir Reference Buaria, Bodenschatz and Pumir2020; Buaria & Pumir Reference Buaria and Pumir2022). We use the corresponding feature, namely $\varSigma \ll \varOmega$, to analyse the magnitudes of the various terms appearing in (3.3). This is at the origin of the simple functional form for $h^p_{ij}$ that we propose in this work.

We first notice that both the operators ${{\rm D}}/{{\rm D} t}$ and $\nu \nabla ^2$ have the dimension of the inverse of a time, $1/T$. Given that the fastest time scale in extreme vorticity regions is $1/\varOmega ^{1/2}$, we estimate that

(3.4a,b)\begin{equation} \left \langle \frac{{\rm D}{{\mathsf{s}}}_{ij} }{{\rm D}t} | \varOmega \right\rangle , \quad \left \langle \nu \nabla^2 {{\mathsf{s}}}_{ij} | \varOmega \right\rangle \lesssim \varSigma^{1/2}\varOmega^{1/2}. \end{equation}

Besides, the second and third terms on the left-hand side of (3.3) scale as

(3.5)\begin{equation} \left \langle {{\mathsf{s}}}_{ik} {{\mathsf{s}}}_{kj} | \varOmega \right\rangle \sim \varSigma \ll \left \langle \tfrac{1}{4}\left(\omega_i \omega_j - \omega^2 \delta_{ij}\right) | \varOmega \right\rangle \sim \varOmega . \end{equation}

Thus the third term dominates the first, second and fifth terms on the left-hand side of (3.3), as a result, we should have $\langle {{\mathsf{h}}\,}^p_{ij} | \varOmega \rangle \sim \langle - \frac {1}{4}(\omega _i \omega _j - \omega ^2 \delta _{ij}) | \varOmega \rangle$ when $\varOmega \tau _K^2 \gg 1$. This argument suggests that the pressure Hessian is determined by the local value of vorticity in extreme vorticity regions. For simplicity, we denote $\tilde {{\mathsf{h}}\,}^p_{ij} \equiv - \frac {1}{4}(\omega _i \omega _j - \omega ^2 \delta _{ij})$ and, subtracting out the trace, we obtain its deviatoric part as

(3.6)\begin{equation} \tilde{{{\mathsf{H}}}\,}^p_{ij} \equiv- \tfrac{1}{4}\left(\omega_i \omega_j - \tfrac{1}{3}\omega^2 \delta_{ij}\right) . \end{equation}

The approximations leading to (3.6) suggest that the difference between ${{\mathsf{H}}\,}^p_{ij}$ and $\tilde {{{\mathsf{H}}}\,}^p_{ij}$ is mostly due to the strain component, which is explicitly neglected in our heurstic derivation. This is consistent with our own numerical results, see e.g. figure 1, which indicate that the average of ${\rm tr} [ ( {\boldsymbol{\mathsf{H}}\kern0.7pt}^p - \tilde {{\boldsymbol{\mathsf{H}}}\kern0.7pt}^p )^2 ]$ conditioned on $\varOmega$ grows as ${\sim }\varOmega ^{2 \gamma }$, whereas the average of ${\rm tr} [ ({\boldsymbol{\mathsf{H}}\kern0.7pt}^p)^2 ]$ conditioned on $\varOmega$ grows as $\sim \varOmega ^2$. This implies, in particular, that the p.d.f. of the difference between ${\boldsymbol{\mathsf{H}}\kern0.7pt}^p$ and its asymptotic form is becoming narrower, in units of $\langle {\rm tr}[ ({\boldsymbol{\mathsf{H}}\kern0.7pt}^p)^2 ] |\varOmega \rangle$ when $\varOmega$ is very large.

Figure 1. Second moment of the deviatoric part of the pressure Hessian tensor, ${\boldsymbol{\mathsf{H}}\kern0.7pt}^p$ (blue line) and of the difference, $({\boldsymbol{\mathsf{H}}\kern0.7pt}^p - \tilde {{\boldsymbol{\mathsf{H}}}\kern0.7pt}^p)$ (red line) conditioned on $\varOmega$. In agreement with the approximation proposed in the text, the second moment of ${\boldsymbol{\mathsf{H}}\kern0.7pt}^p$ grows as $\varOmega ^2$, whereas the second moment of $({\boldsymbol{\mathsf{H}}\kern0.7pt}^p - \tilde {{\boldsymbol{\mathsf{H}}}\kern0.7pt}^p)$ grows as $\varOmega ^{2 \gamma }$, with $\gamma < 1$. Dataset B was used to construct the figure.

3.2. Structure of the pressure Hessian in regions of large vorticity

Before exploring the implications of (3.6) on the dynamics of the velocity gradient tensor, we first discuss the properties of the tensor $\tilde {{\boldsymbol{\mathsf{H}}}\kern0.7pt}^p$, and compare them with the results of DNS.

It is easy to see that the tensor $\tilde {{\mathsf{h}}}^p_{ij} = - \frac {1}{4}(\omega _i \omega _j - \omega ^2 \delta _{ij})$ has a zero eigenvalue in the eigendirection $\hat {\boldsymbol {\omega }}$, along with a degenerate eigenvalue $\frac {1}{4} \omega ^2$, in the plane perpendicular to $\hat {\boldsymbol {\omega }}$. This is generally consistent with DNS results. Nomura & Post (Reference Nomura and Post1998), Lawson & Dawson (Reference Lawson and Dawson2015) and Buaria & Pumir (Reference Buaria and Pumir2023) observed that when $\varOmega \tau _K^2 \gg 1$, $\hat{\boldsymbol{\omega}}$ strongly aligns with eigendirection $\boldsymbol {e}^{ph}_3$ of the pressure Hessian $h^p_{ij}$; and the largest and the smallest eigenvalues of ${{\mathsf{h}}\,}^p_{ij}$ conditioned on large $\varOmega$ tend to approach $\frac {1}{4}\omega ^2$ and $0$; the intermediate one reaching a value slightly smaller than $\frac {1}{4} \omega ^2$. To investigate further the structure of the eigenvalues of ${\boldsymbol{\mathsf{h}}\,}^p$, we study the joint p.d.f. of its invariants. Following Tom et al. (Reference Tom, Carbone and Bragg2021), we define

(3.7)\begin{equation} {{\mathsf{b}}}_{ij} \equiv \left.\left( {{\mathsf{h}}\,}^p_{ij} - \tfrac{1}{3}\delta_{ij} {{\mathsf{h}}\,}^p_{kk} \right) \right/ \sqrt{ {{\mathsf{h}}\,}^p_{ln} {{\mathsf{h}}\,}^p_{ln}} , \end{equation}

where ${\boldsymbol{\mathsf{b}}}$ is the deviatoric part of the pressure Hessian, ${{\mathsf{H}}\,}^p_{ij}$, normalized by the norm of ${\boldsymbol{\mathsf{h}}\,}^p$. Furthermore, we construct the invariants of ${\boldsymbol{\mathsf{b}}}$ as

(3.8a,b)\begin{equation} \zeta =-\sqrt{6} \,{\rm tr}({\boldsymbol{\mathsf{b}}}^3),\quad \chi = \left( {\rm tr}({\boldsymbol{\mathsf{b}}}^2) \right)^{3/2}. \end{equation}

Figure 2 shows the joint p.d.f. of $\zeta$ and $\chi$ for $\varOmega \tau _K^2 = 1$, 4, 25 and $100$, respectively. The eigenvalues of the pressure Hessian exhibit a high-probability region near the configuration corresponding to $\tilde {{\mathsf{h}}}_{ij}^p$, where $\lambda ^p_1 = \lambda ^p_2 = h^p_{ii}/2$ and $\lambda ^p_3 = 0$ so $\chi = \zeta = \sqrt {3}/9 \approx 0.1925$. This configuration is indicated by the green squares in figure 2.

Figure 2. Joint p.d.f. of the dimensionless invariants $\zeta$ and $\chi$ of the pressure Hessian conditioned on (a) $\varOmega \tau _K^2 = 1$, (b) $\varOmega \tau _K^2 = 4$, (c) $\varOmega \tau _K^2 = 25$ and (d) $\varOmega \tau _K^2 = 100$. The red line with cross symbols in (d) corresponds to a Burgers vortex. The white dashed-dotted lines show the iso-probability contours corresponding to the value $1$, and the dashed lines to $2^n$.

We now demonstrate that the structure of the p.d.f.s of $(\zeta, \chi )$ conditioned on $\varOmega \tau _K^2 \gg 1$ is fully consistent with the presence of intense vortex tube-like structure (Siggia Reference Siggia1981; She et al. Reference She, Jackson and Orszag1990; Jiménez et al. Reference Jiménez, Wray, Saffman and Rogallo1993; Ishihara et al. Reference Ishihara, Gotoh and Kaneda2009; Buaria et al. Reference Buaria, Pumir, Bodenschatz and Yeung2019). To this end, we consider a Burgers vortex, characterized by the standard definition of the Reynolds number, $Re = \varGamma /\nu$, where $\varGamma$ is the circulation of the vortex. At the centre of the vortex (Burgers Reference Burgers1948) with $Re \gg 1$, the eigenvalues of the pressure Hessian are also $\frac {1}{4}\omega ^2$, $\frac {1}{4}\omega ^2$ and $0$; and the eigendirection corresponding to the $0$ eigenvalue aligns with $\hat {\boldsymbol {\omega }}$ (Andreotti Reference Andreotti1997; Horiuti Reference Horiuti2001; Horiuti & Takagi Reference Horiuti and Takagi2005). We now compare the structure of the pressure Hessian in a turbulent flow with that in a Burgers vortex, whose properties depend only on the distance $r$ to the axis. Following Andreotti (Reference Andreotti1997), we use the dimensionless radius $r^* = r \, a/\nu$, where $a$ is the external strain rate acting on the vortex. We note that the Reynolds number $Re$ amounts to the vorticity at the centre divided by the external strain $a$. As already stated, the maximum value of the probability in all panels of figure 2, indicated by the green squares, corresponds to the axisymmetric configuration on the axis of the vortex ($r^* = 0$). Furthermore, the dependence of the invariants $\zeta$ and $\chi$ on $r^*$ up to $r^* = 1$ in a Burgers vortex is shown as the red line with crosses in figure 2(d), see also (4) of Andreotti (Reference Andreotti1997). As $r^*$ increases, the solution moves up in the $(\zeta, \chi )$ plane, first towards the left border and then back towards the centre. We note that its variation with respect to Reynolds number $Re$ is negligible. The joint p.d.f. of $(\zeta, \chi )$, particularly the ridges, closely follows the Burgers vortex solution. We also observe that when conditioning on a given value of $\varOmega \tau _K^2$, as done in figure 2, the points at a given value of $(\zeta, \chi )$ away from the maximum, or $\zeta = \chi = \sqrt {3}/9$, correspond to points at some distances away from the centre, or $r^* > 0$, of vortices with increasing intensity. These vortices are therefore less probable, which explains that the maximum probability in figure 2 corresponds to $\zeta = \chi = \sqrt {3}/9$. Additionally, the distribution becomes more concentrated along the red curve when $\varOmega \tau _K^2$ increases. Figure 2 therefore demonstrates that the Burgers vortex model provides a compelling qualitative description of the pressure Hessian. We notice, however, that any axisymmetric vortex model would lead to qualitatively similar observations near the centre of the vortex, consistent with (3.6) for the deviatoric part of the pressure Hessian tensor.

4. Dynamics in the $(R,Q)$ plane

To illustrate the dynamical implications of (3.6), we project the equations of motion for ${\boldsymbol{\mathsf{m}}}$ on the plane $(R,Q)$, where the invariants $R$ and $Q$ are defined by

(4.1)$$\begin{gather} Q \equiv-\tfrac{1}{2}{\mathsf{m}}_{ij}{\mathsf{m}}_{ji} =-\tfrac{1}{2} {{\mathsf{s}}}_{ij}{{\mathsf{s}}}_{ji} + \tfrac{1}{4} \omega^2, \end{gather}$$

(4.2)$$\begin{gather}R \equiv-\tfrac{1}{3}{\mathsf{m}}_{ij}{\mathsf{m}}_{jk}{\mathsf{m}}_{ki} =-\tfrac{1}{3} {{\mathsf{s}}}_{ij}{{\mathsf{s}}}_{jk} {{\mathsf{s}}}_{ki} - \tfrac{1}{4}\omega_i {{\mathsf{s}}}_{ij}\omega_j . \end{gather}$$

In (4.1) and (4.2), and throughout this text, we assume summation of repeated indices. Physically, $Q$ expresses the difference between enstrophy and the square of the strain rate, so $Q = \frac {1}{2} \varOmega - {\rm tr}({\boldsymbol{\mathsf{s}}}^2) > 0$ corresponds to vorticity-dominated regions and $Q<0$ corresponds to strain-dominated regions. Similarly, $R = - \frac {1}{3} {\rm tr}({\boldsymbol{\mathsf{s}}}^2) - \frac {1}{4} \boldsymbol {\omega } \boldsymbol {\cdot } {\boldsymbol{\mathsf{s}}} \boldsymbol {\cdot } \boldsymbol {\omega } <0$ corresponds to the vortex-stretching-dominated region. The exact Lagrangian evolution equations for the invariants $R$ and $Q$ can be readily derived from (1.2):

(4.3)$$\begin{gather} \frac{{\rm d}Q}{{\rm d}t} =- 3 R + {\mathsf{m}}_{ij} {{\mathsf{H}}\,}^p_{ji} - {\mathsf{m}}_{ij} {{\mathsf{H}}}^\nu_{ji}, \end{gather}$$

(4.4)$$\begin{gather}\frac{{\rm d}R}{{\rm d}t} = \frac{2}{3} Q^2 + {\mathsf{m}}_{ij} {\mathsf{m}}_{jk} {{\mathsf{H}}\,}^p_{ki} - {\mathsf{m}}_{ij} {\mathsf{m}}_{jk} {{\mathsf{H}}}^\nu_{ki}, \end{gather}$$

where ${{\mathsf{H}}\,}^p_{ij}$ is the deviatoric part of the pressure Hessian, and ${{\mathsf{H}}}^\nu _{ij} \equiv \nu ({\partial ^2 {\mathsf{m}}_{ij}}/{\partial x_k \partial x_k})$. We stress that these two terms in (4.3) and (4.4) are unclosed. The RE approximation introduced above provides a closure consisting in neglecting the deviatoric contributions to the pressure Hessian: ${\boldsymbol{\mathsf{H}}\kern0.7pt}^p = {\boldsymbol{\mathsf{0}}}$. As mentioned already (Buaria & Pumir Reference Buaria and Pumir2023), the RE assumption fails to predict the qualitative behaviour of the dynamics in the $(R,Q)$ plane when $Q$ is positive and large. Specifically, the RE assumption leads to ${{\rm d}R}/{{\rm d}t} = \frac {2}{3} Q^2 >0$, but the results of DNS show that ${{\rm d}R}/{{\rm d}t} < 0$ in some region of the second quadrant of the $(R, Q)$ plane, see, for example, figures 3(a) and 3(d) of Wilczek & Meneveau (Reference Wilczek and Meneveau2014) and figure 5 of Yang et al. (Reference Yang, Bodenschatz, He, Pumir and Xu2023). The observation that pressure leads to a ‘depression of nonlinearity’ (Borue & Orszag Reference Borue and Orszag1998) suggests the functional ${{\mathsf{H}}\,}^p_{ij} = - \alpha ({\mathsf{m}}_{ik}{\mathsf{m}}_{kj} - \frac {1}{3} {\rm tr}({\boldsymbol{\mathsf{m}}}^2)\delta _{ij})$ where $0 < \alpha < 1$ is a model parameter (Chertkov et al. Reference Chertkov, Pumir and Shraiman1999). This model predicts that the pressure terms induced by ${{\mathsf{H}}\,}^p_{ij}$ in (4.3) and (4.4) anti-align with the RE terms in the $(R,Q)$ plane, in quantitative contradiction with numerical results for $Q > 0$, and particularly for $R < 0$. Attempts to improve the RE approximation have assumed mostly some local expressions for the pressure Hessian, with an explicit relation between ${\boldsymbol{\mathsf{H}}\kern0.7pt}^p$ and the velocity gradient tensor ${\boldsymbol{\mathsf{m}}}$ (Wilczek & Meneveau Reference Wilczek and Meneveau2014). In the following, we will discuss theoretically the role of pressure Hessian in the vorticity-dominated regions, and derive a local analytical expression for the contributions of ${{\mathsf{H}}\,}^p_{ij}$ in Eqs. (4.3) and (4.4), to leading order when $\varOmega \tau _K^2 \gg 1$.

We now use the approximate form of the deviatoric part of the pressure Hessian, (3.6), to analyse the dynamics in the $(R,Q)$ plane. When $\varOmega \tau _K^2 \gg 1$, (3.6) gives

(4.5)$$\begin{gather} {\mathsf{m}}_{ij} \tilde{H}^p_{ji} =-\tfrac{1}{4} \omega_i {{\mathsf{s}}}_{ij} \omega_j = R - \tfrac{1}{3}{{\mathsf{s}}}_{ij}{{\mathsf{s}}}_{jk}{{\mathsf{s}}}_{ki} , \end{gather}$$

(4.6)$$\begin{gather}{\mathsf{m}}_{ij}{\mathsf{m}}_{jk} \tilde{H}^p_{ki} =-\tfrac{2}{3} Q^2 - \tfrac{1}{12} \omega^2 {{\mathsf{s}}}_{ij}{{\mathsf{s}}}_{ji} +\tfrac{1}{6}({{\mathsf{s}}}_{ij} {{\mathsf{s}}}_{ji})^2 - \tfrac{1}{4} \omega_i {{\mathsf{s}}}_{ik}{{\mathsf{s}}}_{kj}\omega_j . \end{gather}$$

We recall that the expressions for ${\rm d}Q/{\rm d}t$ and ${\rm d}R/{\rm d}t$ obtained by using the RE approximation, provided by (4.3) and (4.4) are $- 3R$ and $\frac {2}{3} Q^2$, respectively. In the spirit of the approach in § 3.1, based on the quantitative difference between $\varSigma$ and $\varOmega$, namely with $\varSigma \ll \varOmega$ when $\varOmega \tau _K^2 \gg 1$, we further notice that when $\varOmega \tau _K^2 \gg 1$, $R \gg \frac {1}{3}{{\mathsf{s}}}_{ij}{{\mathsf{s}}}_{jk}{{\mathsf{s}}}_{ki}$, so the ${\boldsymbol{\mathsf{H}}\kern0.7pt}^p$ term cancels, to the leading order in $\varSigma /\varOmega$, approximately $1/3$ of the RE term in the $Q$ equation. More significantly, in the limit $\varOmega \tau _K^2 \gg 1$, we find that $Q^2 \gg \omega ^2 {{\mathsf{s}}}_{ij}{{\mathsf{s}}}_{ji}, \omega _i {{\mathsf{s}}}_{ik}{{\mathsf{s}}}_{kj}\omega _j \gg ({{\mathsf{s}}}_{ij} {{\mathsf{s}}}_{ji})^2$ in the $R$ equation, so the ${\boldsymbol{\mathsf{H}}\kern0.7pt}^p$ terms cancel out the dominant RE term $\frac {2}{3} Q^2$. The lowest-order contribution in a formal development in $(\varSigma /\varOmega )$ involves terms such as $- \frac {1}{12} \omega ^2 {{\mathsf{s}}}_{ij}{{\mathsf{s}}}_{ji} - \frac {1}{4} \omega _i {{\mathsf{s}}}_{ik}{{\mathsf{s}}}_{kj}\omega _j$, which is negative. We observe that this implies ${\rm d}R/{\rm d}t < 0$, which is generally consistent with the DNS results (see e.g. figure 5 of Yang et al. Reference Yang, Bodenschatz, He, Pumir and Xu2023). Earlier work aimed at describing the pressure Hessian (Chevillard et al. Reference Chevillard, Meneveau, Biferale and Toschi2008; Wilczek & Meneveau Reference Wilczek and Meneveau2014) did not particularly focus on high-enstrophy regions. It would be interesting to compare the corresponding predictions in light of the approximation. We note that the tetrad model (Chertkov et al. Reference Chertkov, Pumir and Shraiman1999; Yang et al. Reference Yang, Pumir and Xu2020, Reference Yang, Bodenschatz, He, Pumir and Xu2023) involves quadratic terms in the vorticity introduced through the full tensor ${\boldsymbol{\mathsf{m}}}$, insufficient to compensate for the strong vortex-stretching reduction due to the RE approximation.

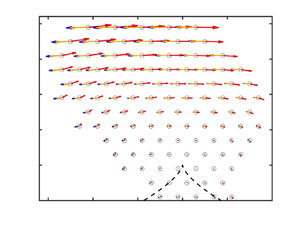
Figure 3(a) shows the DNS results for ${{\rm d}Q}/{{\rm d}t}$ and ${{\rm d}R}/{{\rm d}t}$ on the $(R,Q)$ plane (blue arrows) and compares them with the theoretical predictions (magenta arrows). Figure 3(a) demonstrates that when $Q \tau _K^2 \gtrsim 5$ and $|R \, \tau _K^3|$ is not too large, the magenta arrows, which represent our theoretical predictions (rightmost terms of (4.5), (4.6)), agree well with the blue arrows, which represent the ‘exact’ DNS values. Figure 3 also directly compares the ratios between the numerically determined values ${\rm tr}({\boldsymbol{\mathsf{H}}\kern0.7pt}^p \boldsymbol {\cdot } {\boldsymbol{\mathsf{m}}} )$ (b) and ${\rm tr}({\boldsymbol{\mathsf{H}}\kern0.7pt}^p \boldsymbol {\cdot } {\boldsymbol{\mathsf{m}}}^2 )$ (c) and the values found by replacing ${\boldsymbol{\mathsf{H}}\kern0.7pt}^p$ by $\tilde {{\boldsymbol{\mathsf{H}}}\kern0.7pt}^p$. The agreement for the ${\rm tr}({\boldsymbol{\mathsf{H}}\kern0.7pt}^p \boldsymbol {\cdot } {\boldsymbol{\mathsf{m}}}^2 )$ generally improves when $Q$ increases, as expected when $\varOmega \tau _K^2$ increases. The effect is weaker for the term ${\rm tr}({\boldsymbol{\mathsf{H}}\kern0.7pt}^p \boldsymbol {\cdot } {\boldsymbol{\mathsf{m}}})$. We note that the quality of the agreement at $R \approx 0$ degrades when $Q \tau _K^2$ increases, which is due to the small values of both numerator and denominator. Figure 4 provides further insight on the dynamics, by comparing the contributions of ${\boldsymbol{\mathsf{H}}\kern0.7pt}^p$ to ${{\rm d}Q}/{{\rm d}t}$ and ${{\rm d}R}/{{\rm d}t}$ in the $(R,Q)$ plane, with the leading-order terms in (4.5) and (4.6), namely $R$ and $- \frac {2}{3} Q^2$. Figure 4 reveals that when $Q \tau _K^2 > 5$ and $|R\tau _K^3|$ is not too large, the green arrows, which represent our theoretical predictions to leading order are reassuringly close to the blue arrows, which represent the values obtained directly from DNS.

Figure 3. (a) Results for ${{\rm d}Q}/{{\rm d}t}$ and ${{\rm d}R}/{{\rm d}t}$ in the $(R,Q)$ plane. The red arrows show the RE term $(-3R, \frac {2}{3}Q^2)$, the blue arrows the deviatoric pressure Hessian term $(- {\mathsf{m}}_{ij} {{\mathsf{H}}\,}^p_{ji}, - {\mathsf{m}}_{ij}{\mathsf{m}}_{jk} {{\mathsf{H}}\,}^p_{ki})$ and the magenta arrows our theoretical predictions for large $\varOmega$, i.e. the rightmost terms of (4.5), (4.6). Panels (b,c) show the ratio between the contributions of the deviatoric part of the pressure Hessian, ${\boldsymbol{\mathsf{H}}\kern0.7pt}^p$, and those of the approximate form, $\tilde {{\boldsymbol{\mathsf{H}}}\kern0.7pt}^p$, (3.6), to ${\rm d} Q/{\rm d}t$ (b) and ${\rm d}R/{\rm d}t$ (c). The ratios, plotted as a function of $R \tau _K^3$, increase towards $1$ as $Q \tau _K^2$ increases. The large value for ${\rm d}Q/{\rm d}t$ close to $R \tau _K^3 \approx 0$ corresponds to very small values of both the terms ${\rm tr}({\boldsymbol{\mathsf{H}}\kern0.7pt}^p \boldsymbol {\cdot } {\boldsymbol{\mathsf{m}}})$ and ${\rm tr}(\tilde {{\boldsymbol{\mathsf{H}}}\kern0.7pt}^p \boldsymbol {\cdot } {\boldsymbol{\mathsf{m}}})$. Dataset B was used to construct the figure.

Figure 4. (a) Pressure contribution to ${{\rm d}Q}/{{\rm d}t}$ and ${{\rm d}R}/{{\rm d}t}$ in the $(R,Q$) plane. The red arrows correspond to the RE term $(-3R, \frac {2}{3}Q^2)$, which corresponds to the isotropic (local) contribution of the pressure Hessian, the blue arrows to the anisotropic pressure Hessian term $(- {\mathsf{m}}_{ij} H^p_{ji}, - {\mathsf{m}}_{ij}{\mathsf{m}}_{jk} H^p_{ki})$ and the green arrows show the simplified theoretical predictions at large $\varOmega$, $(R, -\frac {2}{3}Q^2)$. Panel (b) shows the ratio between the contribution of ${\boldsymbol{\mathsf{H}}\kern0.7pt}^p$ to ${\rm d}R/{\rm d}t$, compared with the simplified form $-2 Q^2/3$. Dataset B ($R_\lambda = 210$) was used to construct the figure.

Remarkably, we notice that using $-\frac {2}{3} Q^2$ for the contribution due to the deviatoric part of the pressure Hessian leads to ${\rm d}R/{\rm d}t = 0$ in the inviscid case. Whether the blue arrows in figure 4(a) are longer or shorter than the green ones in fact determines the sign of ${\rm d}R/{\rm d}t$. We observe that ${\rm d}R/{\rm d}t > 0$ when $Q \tau _K^2 \gtrsim 20$ for Dataset B with $R_\lambda = 210$. At lower values of $Q \tau _K^2$, and for $R \tau _K^3$ sufficiently negative, on the contrary, ${\rm d}R/{\rm d}t < 0$. For these values, the dynamics tends to keep the values $(R,Q)$ in the ($R < 0, Q > 0$) quadrant, where stretching is largest. This contrasts sharply with the predictions of the RE approximation, which tends to inhibit vortex stretching (Buaria & Pumir Reference Buaria and Pumir2023). A more precise comparison between ${\rm tr}( {\boldsymbol{\mathsf{H}}\kern0.7pt}^p \boldsymbol {\cdot } {\boldsymbol{\mathsf{m}}}^2)$ and $-\frac {2}{3} Q^2$ is shown in figure 4(b). At relatively low value of $Q \tau _K^2$, and for $R \tau _K^3 \lesssim -3$, ${\rm tr} ({\boldsymbol{\mathsf{H}}\kern0.7pt}^p \boldsymbol {\cdot } {\boldsymbol{\mathsf{m}}}^2 )$ is more negative than $-\frac {2}{3} Q^2$, consistent with the observation that ${\rm d}R/{\rm d}t < 0$. As $Q \tau _K^2$ increases, however, the region where ${\rm d}R/{\rm d}t < 0$ is restricted to much larger values of $R \tau _K^3 < 0$, whereas at small, intermediate values of $|R\tau_K^3|$, ${\rm d}R/{\rm d}t > 0$.