Article contents
The structure of the absolutely unstable regions in the near field of low-density jets
Published online by Cambridge University Press: 17 October 2012
Abstract
The viscous spatiotemporal stability properties of low-density laminar round jets emerging from circular nozzles or tubes are investigated numerically providing, for the first time, a separate treatment of the two particular cases typically studied in experiments: a hot gas jet discharging into a quiescent cold ambient of the same species, and an isothermal jet consisting of a mixture of two gases with different molecular weight, discharging into a stagnant ambient of the heavier species. To that end, use is made of a realistic representation for the base velocity and density profiles based on boundary-layer theory, with account taken of the effect of variable transport properties. Our results show significant quantitative differences with respect to previous parametric studies, and reveal that hot jets are generically more unstable than light jets, in the sense that they have larger associated critical density ratios for values of the Reynolds number and momentum thickness typically used in experiments. In addition, for several values of the jet-to-ambient density ratio, 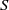 $S$ , the downstream evolution of the local stability properties of the jet is computed as a function of the two main control parameters governing the jet, namely the Reynolds number,
$S$ , the downstream evolution of the local stability properties of the jet is computed as a function of the two main control parameters governing the jet, namely the Reynolds number, 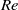 $\mathit{Re}$ , and the momentum thickness of the initial velocity profile,
$\mathit{Re}$ , and the momentum thickness of the initial velocity profile, 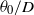 ${\theta }_{0} / D$ . It is shown that, for a given value of
${\theta }_{0} / D$ . It is shown that, for a given value of 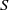 $S$ , the
$S$ , the 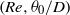 $(\mathit{Re}, {\theta }_{0} / D)$ parameter plane can be divided in three regions. In the first region, defined by low values of
$(\mathit{Re}, {\theta }_{0} / D)$ parameter plane can be divided in three regions. In the first region, defined by low values of 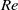 $\mathit{Re}$ or very thick shear layers, the flow is locally convectively unstable everywhere. In the second region, with moderately large values of
$\mathit{Re}$ or very thick shear layers, the flow is locally convectively unstable everywhere. In the second region, with moderately large values of 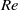 $\mathit{Re}$ and thin shear layers, the jet exhibits a localized pocket of absolute instability, away from boundaries. Finally, in the third region, that prevails in most of the
$\mathit{Re}$ and thin shear layers, the jet exhibits a localized pocket of absolute instability, away from boundaries. Finally, in the third region, that prevails in most of the 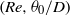 $(\mathit{Re}, {\theta }_{0} / D)$ parameter plane, the absolutely unstable domain is bounded by the jet outlet. All the experiments available in the literature are shown to lie in the latter region, and the global transition observed in experiments is demonstrated to take place when the absolutely unstable domain becomes sufficiently large. The marginal frequency of the resulting global self-excited oscillations is shown to be fairly well described by the absolute frequency evaluated at the jet outlet, in agreement with the numerical results obtained by Lesshafft et al. (J. Fluid Mech., vol. 554, 2006, pp. 393–409) for synthetic jets.
$(\mathit{Re}, {\theta }_{0} / D)$ parameter plane, the absolutely unstable domain is bounded by the jet outlet. All the experiments available in the literature are shown to lie in the latter region, and the global transition observed in experiments is demonstrated to take place when the absolutely unstable domain becomes sufficiently large. The marginal frequency of the resulting global self-excited oscillations is shown to be fairly well described by the absolute frequency evaluated at the jet outlet, in agreement with the numerical results obtained by Lesshafft et al. (J. Fluid Mech., vol. 554, 2006, pp. 393–409) for synthetic jets.
Information
- Type
- Papers
- Information
- Copyright
- ©2012 Cambridge University Press
References
- 22
- Cited by

