Article contents
Surfactant and gravity dependent instability of two-layer Couette flows and its nonlinear saturation
Published online by Cambridge University Press: 03 August 2017
Abstract
A horizontal channel flow of two immiscible fluid layers with different densities, viscosities and thicknesses, subject to vertical gravitational forces and with an insoluble surfactant monolayer present at the interface, is investigated. The base Couette flow is driven by the uniform horizontal motion of the channel walls. Linear and nonlinear stages of the (inertialess) surfactant and gravity dependent long-wave instability are studied using the lubrication approximation, which leads to a system of coupled nonlinear evolution equations for the interface and surfactant disturbances. The (inertialess) instability is a combined result of the surfactant action characterized by the Marangoni number 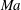 $Ma$ and the gravitational effect corresponding to the Bond number
$Ma$ and the gravitational effect corresponding to the Bond number 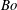 $Bo$ that ranges from
$Bo$ that ranges from 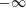 $-\infty$ to
$-\infty$ to 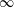 $\infty$ . The other parameters are the top-to-bottom thickness ratio
$\infty$ . The other parameters are the top-to-bottom thickness ratio  $n$ , which is restricted to
$n$ , which is restricted to  $n\geqslant 1$ by a reference frame choice, the top-to-bottom viscosity ratio
$n\geqslant 1$ by a reference frame choice, the top-to-bottom viscosity ratio 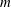 $m$ and the base shear rate
$m$ and the base shear rate  $s$ . The linear stability is determined by an eigenvalue problem for the normal modes, where the complex eigenvalues (determining growth rates and phase velocities) and eigenfunctions (the amplitudes of disturbances of the interface, surfactant, velocities and pressures) are found analytically by using the smallness of the wavenumber. For each wavenumber, there are two active normal modes, called the surfactant and the robust modes. The robust mode is unstable when
$s$ . The linear stability is determined by an eigenvalue problem for the normal modes, where the complex eigenvalues (determining growth rates and phase velocities) and eigenfunctions (the amplitudes of disturbances of the interface, surfactant, velocities and pressures) are found analytically by using the smallness of the wavenumber. For each wavenumber, there are two active normal modes, called the surfactant and the robust modes. The robust mode is unstable when 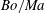 $Bo/Ma$ falls below a certain value dependent on
$Bo/Ma$ falls below a certain value dependent on 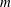 $m$ and
$m$ and  $n$ . The surfactant branch has instability for
$n$ . The surfactant branch has instability for 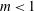 $m<1$ , and any
$m<1$ , and any 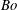 $Bo$ , although the range of unstable wavenumbers decreases as the stabilizing effect of gravity represented by
$Bo$ , although the range of unstable wavenumbers decreases as the stabilizing effect of gravity represented by 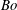 $Bo$ increases. Thus, for certain parametric ranges, even arbitrarily strong gravity cannot completely stabilize the flow. The correlations of vorticity-thickness phase differences with instability, present when gravitational effects are neglected, are found to break down when gravity is important. The physical mechanisms of instability for the two modes are explained with vorticity playing no role in them. This is in marked contrast to the dynamical role of vorticity in the mechanism of the well-known Yih instability due to effects of inertia, and is contrary to some earlier literature. Unlike the semi-infinite case that we previously studied, a small-amplitude saturation of the surfactant instability is possible in the absence of gravity. For certain
$Bo$ increases. Thus, for certain parametric ranges, even arbitrarily strong gravity cannot completely stabilize the flow. The correlations of vorticity-thickness phase differences with instability, present when gravitational effects are neglected, are found to break down when gravity is important. The physical mechanisms of instability for the two modes are explained with vorticity playing no role in them. This is in marked contrast to the dynamical role of vorticity in the mechanism of the well-known Yih instability due to effects of inertia, and is contrary to some earlier literature. Unlike the semi-infinite case that we previously studied, a small-amplitude saturation of the surfactant instability is possible in the absence of gravity. For certain 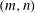 $(m,n)$ -ranges, the interface deflection is governed by a decoupled Kuramoto–Sivashinsky equation, which provides a source term for a linear convection–diffusion equation governing the surfactant concentration. When the diffusion term is negligible, this surfactant equation has an analytic solution which is consistent with the full numerics. Just like the interface, the surfactant wave is chaotic, but the ratio of the two waves turns out to be constant.
$(m,n)$ -ranges, the interface deflection is governed by a decoupled Kuramoto–Sivashinsky equation, which provides a source term for a linear convection–diffusion equation governing the surfactant concentration. When the diffusion term is negligible, this surfactant equation has an analytic solution which is consistent with the full numerics. Just like the interface, the surfactant wave is chaotic, but the ratio of the two waves turns out to be constant.
Information
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 16
- Cited by


