Article contents
The Taylor–Melcher leaky dielectric model as a macroscale electrokinetic description
Published online by Cambridge University Press: 14 May 2015
Abstract
While the Taylor–Melcher electrohydrodynamic model entails ionic charge carriers, it addresses neither ionic transport within the liquids nor the formation of diffuse space-charge layers about their common interface. Moreover, as this model is hinged upon the presence of non-zero interfacial-charge density, it appears to be in contradiction with the aggregate electro-neutrality implied by ionic screening. Following a brief synopsis published by Baygents & Saville (Third International Colloquium on Drops and Bubbles, AIP Conference Proceedings, vol. 7, 1989, American Institute of Physics, pp. 7–17) we systematically derive here the macroscale description appropriate for leaky dielectric liquids, starting from the primitive electrokinetic equations and addressing the double limit of thin space-charge layers and strong fields. This derivation is accomplished through the use of matched asymptotic expansions between the narrow space-charge layers adjacent to the interface and the electro-neutral bulk domains, which are homogenized by the strong ionic advection. Electrokinetic transport within the electrical ‘triple layer’ comprising the genuine interface and the adjacent space-charge layers is embodied in effective boundary conditions; these conditions, together with the simplified transport within the bulk domains, constitute the requisite macroscale description. This description essentially coincides with the familiar equations of Melcher & Taylor (Annu. Rev. Fluid Mech., vol. 1, 1969, pp. 111–146). A key quantity in our macroscale description is the ‘apparent’ surface-charge density, provided by the transversely integrated triple-layer microscale charge. At leading order, this density vanishes due to the expected Debye-layer screening; its asymptotic correction provides the ‘interfacial’ surface-charge density appearing in the Taylor–Melcher model. Our unified electrohydrodynamic treatment provides a reinterpretation of both the Taylor–Melcher conductivity-ratio parameter and the electrical Reynolds number. The latter, expressed in terms of fundamental electrokinetic properties, becomes 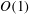 $O(1)$ only for intense applied fields, comparable with the transverse field within the space-charge layers; at this limit the asymptotic scheme collapses. Surface-charge advection is accordingly absent in the macroscale description. Owing to the inevitable presence of (screened) net charge on the genuine interface, the drop also undergoes electrophoretic motion. The associated flow, however, is asymptotically smaller than that corresponding to the Taylor–Melcher circulation. Our successful matching procedure contrasts the analysis of Baygents & Saville, who considered more general electrolytes and were unable to directly match the inner and outer regions. We discuss this difference in detail.
$O(1)$ only for intense applied fields, comparable with the transverse field within the space-charge layers; at this limit the asymptotic scheme collapses. Surface-charge advection is accordingly absent in the macroscale description. Owing to the inevitable presence of (screened) net charge on the genuine interface, the drop also undergoes electrophoretic motion. The associated flow, however, is asymptotically smaller than that corresponding to the Taylor–Melcher circulation. Our successful matching procedure contrasts the analysis of Baygents & Saville, who considered more general electrolytes and were unable to directly match the inner and outer regions. We discuss this difference in detail.
Information
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 109
- Cited by


