Article contents
Three-dimensional Lagrangian Voronoï analysis for clustering of particles and bubbles in turbulence
Published online by Cambridge University Press: 06 January 2012
Abstract
Three-dimensional Voronoï analysis is used to quantify the clustering of inertial particles in homogeneous isotropic turbulence using data sets from numerics in the point particle limit and one experimental data set. We study the clustering behaviour at different density ratios, particle response times (i.e. Stokes numbers 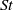 ) and two Taylor–Reynolds numbers (
) and two Taylor–Reynolds numbers (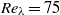 and 180). The probability density functions (p.d.f.s) of the Voronoï cell volumes of light and heavy particles show different behaviour from that of randomly distributed particles, i.e. fluid tracers, implying that clustering is present. The standard deviation of the p.d.f. normalized by that of randomly distributed particles is used to quantify the clustering. The clustering for both light and heavy particles is stronger for higher
and 180). The probability density functions (p.d.f.s) of the Voronoï cell volumes of light and heavy particles show different behaviour from that of randomly distributed particles, i.e. fluid tracers, implying that clustering is present. The standard deviation of the p.d.f. normalized by that of randomly distributed particles is used to quantify the clustering. The clustering for both light and heavy particles is stronger for higher 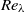 . Light particles show maximum clustering for
. Light particles show maximum clustering for 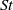 around 1–2 for both Taylor–Reynolds numbers. The experimental data set shows reasonable agreement with the numerical results. The results are consistent with previous investigations employing other approaches to quantify the clustering. We also present the joint p.d.f.s of enstrophy and Voronoï volumes and their Lagrangian autocorrelations. The small Voronoï volumes of light particles correspond to regions of higher enstrophy than those of heavy particles, indicating that light particles cluster in higher vorticity regions. The Lagrangian temporal autocorrelation function of Voronoï volumes shows that the clustering of light particles lasts much longer than that of heavy or neutrally buoyant particles. Due to inertial effects arising from the density contrast with the surrounding liquid, light and heavy particles remain clustered for much longer times than the flow structures which cause the clustering.
around 1–2 for both Taylor–Reynolds numbers. The experimental data set shows reasonable agreement with the numerical results. The results are consistent with previous investigations employing other approaches to quantify the clustering. We also present the joint p.d.f.s of enstrophy and Voronoï volumes and their Lagrangian autocorrelations. The small Voronoï volumes of light particles correspond to regions of higher enstrophy than those of heavy particles, indicating that light particles cluster in higher vorticity regions. The Lagrangian temporal autocorrelation function of Voronoï volumes shows that the clustering of light particles lasts much longer than that of heavy or neutrally buoyant particles. Due to inertial effects arising from the density contrast with the surrounding liquid, light and heavy particles remain clustered for much longer times than the flow structures which cause the clustering.
Information
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 97
- Cited by

