Article contents
Time evolution of uniform momentum zones in a turbulent boundary layer
Published online by Cambridge University Press: 13 March 2018
Abstract
Time-resolved planar particle image velocimetry was used to analyse the structuring of a turbulent boundary layer into uniform momentum zones (UMZs). The instantaneous peak-detection method employed by Adrian et al. (J. Fluid Mech., vol. 422, 2000, pp. 1–54) and de Silva et al. (J. Fluid Mech., vol. 786, 2016, pp. 309–331) is extended to account for temporal coherence of UMZs. The resulting number of zones detected appears to follow a normal distribution at any given instant. However, the extreme cases in which the number of zones is either very high or very low, are shown to be linked with two distinct flow states. A higher than average number of zones is associated with a large-scale 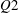 $Q2$ event in the log region which creates increased small-scale activity within that region. Conversely, a low number of zones corresponds to a large-scale
$Q2$ event in the log region which creates increased small-scale activity within that region. Conversely, a low number of zones corresponds to a large-scale 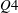 $Q4$ event in the log region and decreased turbulent activity away from the wall. The residence times, within the measurement plane, of zones belonging to the latter scenario are shown to be on average four times larger than those of zones present during higher than average zone structuring states. For both cases, greater residence times are observed for zones of higher momentum that are generally closer to the free stream.
$Q4$ event in the log region and decreased turbulent activity away from the wall. The residence times, within the measurement plane, of zones belonging to the latter scenario are shown to be on average four times larger than those of zones present during higher than average zone structuring states. For both cases, greater residence times are observed for zones of higher momentum that are generally closer to the free stream.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
Laskari et al. supplementary movie 1
Time evolution of all instantaneously detected zones. For the time-sequence of velocity contours (left), the resulting probability density function (pdf) of U is shown in the middle. The peaks of the pdf (representing modal velocities) are marked with coloured symbols (colours according to the velocity value at each peak) for time coherent zones, and grey symbols for short-lived ones. The velocities marking the edge of the zones are shown with dashed lines on the pdf and correspond to the black solid lines demarkating each zone in physical space on the right. The time evolution of the thickness of each zone is presented on the right, where each zone is coloured according to its modal velocity.
Laskari et al. supplementary movie 2
Time evolution and ranking of time-coherent zones. For the time-sequence of velocity contours (left), the resulting probability density function (pdf) of U is shown in the middle for the same sequence as in movie 1, with all short-lived peaks removed. The remaining peaks for the time coherent zones are ranked in ascending order according to their momentum deficit level, effectively labelling the zone closest to the freestream as rank one, while the rank of the zone closest to the wall is equal to the total number of zones present in that particular image. Symbols denote different ranks. The time evolution of the thickness of each zone is presented on the right, where each zone is coloured according to its rank.
- 56
- Cited by


