Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-16T22:36:29.267Z Has data issue: false hasContentIssue false
  • English
  • Français

Topology of three-dimensional steady cellular flow in a two-sided anti-parallel lid-driven cavity

Published online by Cambridge University Press:  03 August 2017

Francesco Romanò Open the ORCID record for Francesco Romanò [Opens in a new window] ,
Stefan Albensoeder  and
Hendrik C. Kuhlmann
Francesco Romanò*
Affiliation:
Institute of Fluid Mechanics and Heat Transfer, TU Wien, Getreidemarkt 9, 1060 Vienna, Austria
Stefan Albensoeder
Affiliation:
School of Mathematics and Science, Carl von Ossietzky Universität, 26111 Oldenburg, Germany
Hendrik C. Kuhlmann
Affiliation:
Institute of Fluid Mechanics and Heat Transfer, TU Wien, Getreidemarkt 9, 1060 Vienna, Austria
*
†Email address for correspondence: francesco.romano@tuwien.ac.at
Get access Rights & Permissions [Opens in a new window]

Abstract

The structure of the incompressible steady three-dimensional flow in a two-sided anti-symmetrically lid-driven cavity is investigated for an aspect ratio 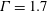$\unicode[STIX]{x1D6E4}=1.7$ and spanwise-periodic boundary conditions. Flow fields are computed by solving the Navier–Stokes equations with a fully spectral method on 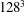$128^{3}$ grid points utilizing second-order asymptotic solutions near the singular corners. The supercritical flow arises in the form of steady rectangular convection cells within which the flow is point symmetric with respect to the cell centre. Global streamline chaos occupying the whole domain is found immediately above the threshold to three-dimensional flow. Beyond a certain Reynolds number the chaotic sea recedes from the interior, giving way to regular islands. The regular Kolmogorov–Arnold–Moser tori grow with increasing Reynolds number before they shrink again to eventually vanish completely. The global chaos at onset is traced back to the existence of one hyperbolic and two elliptic periodic lines in the basic flow. The singular points of the three-dimensional flow which emerge from the periodic lines quickly change such that, for a wide range of supercritical Reynolds number, each periodic convection cell houses a double spiralling-in saddle focus in its centre, a spiralling-out saddle focus on each of the two cell boundaries and two types of saddle limit cycle on the walls. A representative analysis for 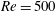$\mathit{Re}=500$ shows chaotic streamlines to be due to chaotic tangling of the two-dimensional stable manifold of the central spiralling-in saddle focus and the two-dimensional unstable manifold of the central wall limit cycle. Embedded Kolmogorov–Arnold–Moser tori and the associated closed streamlines are computed for several supercritical Reynolds numbers owing to their importance for particle transport.

JFM classification

Mixing: Chaotic advection Nonlinear Dynamical Systems: Nonlinear Dynamical Systems Mathematical Foundations: Topological fluid dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 826 , 10 September 2017 , pp. 302 - 334
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aidun, C. K., Triantafillopoulos, N. G. & Benson, J. D. 1991 Global stability of a lid-driven cavity with throughflow: flow visualization studies. Phys. Fluids 3 (9), 2081–2091.Google Scholar
Albensoeder, S. & Kuhlmann, H. C. 2002 Linear stability of rectangular cavity flows driven by anti-parallel motion of two facing walls. J. Fluid Mech. 458, 153–180.CrossRefGoogle Scholar
Albensoeder, S. & Kuhlmann, H. C. 2003 Stability balloon for the double-lid-driven cavity flow. Phys. Fluids 15, 2453–2456.Google Scholar
Albensoeder, S. & Kuhlmann, H. C. 2005 Accurate three-dimensional lid-driven cavity flow. J. Comput. Phys. 206 (2), 536–558.Google Scholar
Albensoeder, S. & Kuhlmann, H. C. 2006 Nonlinear three-dimensional flow in the lid-driven square cavity. J. Fluid Mech. 569, 465–480.Google Scholar
Albensoeder, S., Kuhlmann, H. C. & Rath, H. J. 2001a Multiplicity of steady two-dimensional flows in two-sided lid-driven cavities. Theor. Comput. Fluid Dyn. 14, 223–241.Google Scholar
Albensoeder, S., Kuhlmann, H. C. & Rath, H. J. 2001b Three-dimensional centrifugal-flow instabilities in the lid-driven-cavity problem. Phys. Fluids 13 (1), 121–135.CrossRefGoogle Scholar
Alleborn, N., Raszillier, H. & Durst, F. 1999 Lid-driven cavity with heat and mass transport. Intl J. Heat Mass Transfer 42 (5), 833–853.Google Scholar
Anderson, P. D., Galaktionov, O. S., Peters, G. W. M., van de Vosse, F. N. & Meijer, H. E. H. 2000 Chaotic fluid mixing in non-quasi-static time-periodic cavity flows. Intl J. Heat Fluid Flow 21 (2), 176–185.CrossRefGoogle Scholar
Aref, H. 1984 Stirring by chaotic advection. J. Fluid Mech. 143, 1–21.Google Scholar
Aref, H. 1990 Chaotic advection of fluid particles. Phil. Trans. R. Soc. Lond. A 333 (1631), 273–288.Google Scholar
Arter, W. 1983 Ergodic stream-lines in steady convection. Phys. Lett. A 97, 171–174.Google Scholar
Bajer, K. 1994 Hamiltonian formulation of the equations of streamlines in three-dimensional steady flows. Chaos Solitons Fractals 4 (6), 895–911.Google Scholar
Batchelor, G. K. 1956 On steady laminar flow with closed streamlines at large Reynolds number. J. Fluid Mech. 1, 177–190.CrossRefGoogle Scholar
Bayly, B. J. 1986 Three-dimensional instability of elliptical flow. Phys. Rev. Lett. 57, 2160–2163.Google Scholar
Benjamin, D. F., Anderson, T. J. & Scriven, L. E. 1995 Multiple roll systems: steady-state operation. Am. Inst. Chem. Engrs J. 41 (5), 1045–1060.Google Scholar
Berrut, J.-P. & Trefethen, L. N. 2004 Barycentric Lagrange interpolation. SIAM Rev. 46 (3), 501–517.Google Scholar
Biemond, J. J. B., de Moura, A. P. S., Károlyi, G., Grebogi, C. & Nijmeijer, H. 2008 Onset of chaotic advection in open flows. Phys. Rev. E 78, 016317.Google Scholar
Blohm, C.2001 Experimentelle Untersuchung stationärer und zeitabhängiger Strömungen im zweiseitig angetriebenen Rechteckbehälter. PhD thesis, University of Bremen.Google Scholar
Blohm, C. H. & Kuhlmann, H. C. 2002 The two-sided lid-driven cavity: experiments on stationary and time-dependent flows. J. Fluid Mech. 450, 67–95.CrossRefGoogle Scholar
Botella, O.1998 Résolution numérique de problèmes de Navier–Stokes singuliers par une méthode de projection tchebychev. PhD thesis, Université de Nice.Google Scholar
Botella, O. & Peyret, R. 1998 Benchmark spectral results on the lid-driven cavity flow. Comput. Fluids 27 (4), 421–433.Google Scholar
Botella, O. & Peyret, R. 2001 Computing singular solutions of the Navier–Stokes equations with the Chebyshev-collocation method. Intl J. Numer. Meth. Fluids 36 (2), 125–163.Google Scholar
Boyland, P. L., Aref, H. & Stremler, M. A. 2000 Topological fluid mechanics of stirring. J. Fluid Mech. 403, 277–304.CrossRefGoogle Scholar
Brøns, M. & Hartnack, J. N. 1999 Streamline topologies near simple degenerate critical points in two-dimensional flow away from boundaries. Phys. Fluids 11, 314–324.CrossRefGoogle Scholar
Broomhead, D. S. & Ryrie, S. C. 1988 Particle paths in wavy vortices. Nonlinearity 1 (3), 409–434.CrossRefGoogle Scholar
Bruneau, C.-H. & Saad, M. 2006 The 2d lid-driven cavity problem revisited. Comput. Fluids 35 (3), 326–348.Google Scholar
Burggraf, O. R. 1966 Analytical and numerical studies of the structure of steady separated flows. J. Fluid Mech. 24, 113–151.Google Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zang, T. A. 1988 Spectral Methods in Fluid Dynamics. Springer.CrossRefGoogle Scholar
Chernikov, A. A. & Schmidt, G. 1992 Chaotic streamlines in convective cells. Phys. Lett. A 169, 51–56.Google Scholar
Chien, W.-L., Rising, H. & Ottino, J. M. 1986 Laminar mixing and chaotic mixing in several cavitiy flows. J. Fluid Mech. 170, 355–377.CrossRefGoogle Scholar
Contreras, P. S., de la Cruz, L. M. & Ramos, E. 2016 Topological analysis of a mixing flow generated by natural convection. Phys. Fluids 28 (1), 013602.Google Scholar
Crighton, D. G. 1991 Airframe noise. In Aeroacoustics of Flight Vehicles: Theory and Practice. Volume 1: Noise Sources (ed. Hubbard, H. H.), vol. 1, pp. 391–447. NASA Office of Management, Scientific and Technical Information Program.Google Scholar
Dombre, T., Frisch, U., Greene, J. M., Hénon, M., Mehr, A. & Soward, A. M. 1986 Chaotic streamlines in the ABC flows. J. Fluid Mech. 167, 353–391.CrossRefGoogle Scholar
Dominguez-Lerma, M. A., Cannell, D. S. & Ahlers, G. 1986 Eckhaus boundary and wavenumber selection in rotating Couette–Taylor flow. Phys. Rev. A 34, 4956–4970.Google Scholar
Dormand, J. R. & Prince, P. J. 1980 A family of embedded Runge–Kutta formulae. J. Comput. Appl. Maths 6 (1), 19–26.CrossRefGoogle Scholar
Freitas, C. J. & Street, R. L. 1988 Non-linear transient phenomena in a complex recirculating flow: a numerical investigation. Intl J. Numer. Meth. Fluids 8 (7), 769–802.CrossRefGoogle Scholar
Gaskell, P. H., Gürcan, F., Savage, M. D. & Thompson, H. M. 1998 Stokes flow in a double-lid-driven cavity with free surface side walls. Proc. Inst. Mech. Engrs C 212 (5), 387–403.Google Scholar
Gaskell, P. H., Summers, J. L., Thompson, H. M. & Savage, M. D. 1996 Creeping flow analyses of free surface cavity flows. Theor. Comput. Fluid Dyn. 8 (6), 415–433.Google Scholar
Ghia, U., Ghia, K. N. & Shin, C. T. 1982 High-Re solutions for incompressible flow using the Navier–Stokes equations and a multigrid method. J. Comput. Phys. 48, 387–411.CrossRefGoogle Scholar
Guckenheimer, J. & Holmes, P. 1983 Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, Applied Mathematical Sciences, vol. 42. Springer.CrossRefGoogle Scholar
Haller, G. 2001 Distinguished material surfaces and coherent structures in three-dimensional fluid flows. Physica D 149 (4), 248–277.Google Scholar
Hofmann, E. & Kuhlmann, H. C. 2011 Particle accumulation on periodic orbits by repeated free surface collisions. Phys. Fluids 23 (7), 072106.CrossRefGoogle Scholar
Hwang, W. R., Anderson, P. D. & Hulsen, M. A. 2005 Chaotic advection in a cavity flow with rigid particles. Phys. Fluids 17, 043602.CrossRefGoogle Scholar
Ishii, K. & Adachi, S. 2006 Numerical analysis of 3d vortical cavity flow. Proc. Appl. Maths Mech. 6, 871–874.Google Scholar
Ishii, K. & Iwatsu, R. 1990 Numerical simulation of the Lagrangian flow structure in a driven cavity. In Topological Fluid Mechanics (ed. Moffatt, H. K. & Tsinober, A.), pp. 54–63. Cambridge University Press.Google Scholar
Ishii, K., Ota, C. & Adachi, S. 2012 Streamlines near a closed curve and chaotic streamlines in steady cavity flows. Procedia IUTAM 5, 173–186.Google Scholar
Iwatsu, R., Ishii, K., Kawamura, T., Kuwahara, K. & Hyun, J. M. 1989 Numerical simulation of three-dimensional flow structure in a driven cavity. Fluid Dyn. Res. 5 (3), 173.CrossRefGoogle Scholar
Kroujiline, D. & Stone, H. A. 1999 Chaotic streamlines in steady bounded three-dimensional Stokes flows. Physica D 130, 105–132.Google Scholar
Kuhlmann, H. C., Romanò, F., Wu, H. & Albensoeder, S. 2016 Particle-motion attractors due to particle–boundary interaction in incompressible steady three-dimensional flows. In The 20th Australasian Fluid Mechanics Conference (ed. Ivey, G., Zhou, T., Jones, N. & Draper, S.), vol. 102, p. 449. Australasian Fluid Mechanics Society.Google Scholar
Kuhlmann, H. C., Wanschura, M. & Rath, H. J. 1997 Flow in two-sided lid-driven cavities: non-uniqueness, instabilities, and cellular structures. J. Fluid Mech. 336, 267–299.Google Scholar
Leong, C. W. & Ottino, J. M. 1989 Experiments on mixing due to chaotic advection in a cavity. J. Fluid Mech. 209, 463–499.CrossRefGoogle Scholar
Moffatt, H. K. 1964 Viscous and resistive eddies near a sharp corner. J. Fluid Mech. 18, 1–18.CrossRefGoogle Scholar
Mukin, R. V. & Kuhlmann, H. C. 2013 Topology of hydrothermal waves in liquid bridges and dissipative structures of transported particles. Phys. Rev. E 88 (5), 053016.Google Scholar
Muldoon, F. H. & Kuhlmann, H. C. 2013 Coherent particulate structures by boundary interaction of small particles in confined periodic flows. Physica D 253, 40–65.Google Scholar
Muldoon, F. H. & Kuhlmann, H. C. 2016 Origin of particle accumulation structures in liquid bridges: particle–boundary interactions versus inertia. Phys. Fluids 28, 073305.Google Scholar
Oteski, L., Duguet, Y., Pastur, L. & Quéré, P. L. 2015 Quasiperiodic routes to chaos in confined two-dimensional differential convection. Phys. Rev. E 92, 043020.Google Scholar
Ottino, J. M. 1989 The Kinematics of Mixing: Stretching, Chaos, and Transport, vol. 3. Cambridge University Press.Google Scholar
Ottino, J. M. 1990 Mixing, chaotic advection, and turbulence. Annu. Rev. Fluid Mech. 22 (1), 207–254.Google Scholar
Ottino, J. M. & Khakhar, D. V. 2000 Mixing and segregation of granular materials. Annu. Rev. Fluid Mech. 32, 55–91.Google Scholar
Pai, S. A., Prakash, P. & Patnaik, B. S. V. 2013 Numerical simulation of chaotic mixing in lid driven cavity: effect of passive plug. Engng Appl. Comput. Fluid Mech. 7 (3), 406–418.Google Scholar
Peyret, R. 2013 Spectral Methods for Incompressible Viscous Flow, vol. 148. Springer.Google Scholar
Phillips, T. N. & Roberts, G. W. 1993 The treatment of spurious pressure modes in spectral incompressible flow calculations. J. Comput. Phys. 105 (1), 150–164.CrossRefGoogle Scholar
Pierrehumbert, R. T. 1986 Universal short-wave instability of two-dimensional eddies in an inviscid fluid. Phys. Rev. Lett. 57, 2157–2159.CrossRefGoogle Scholar
Ramanan, N. & Homsy, G. M. 1994 Linear stability of lid-driven cavity flow. Phys. Fluids 6, 2690–2701.Google Scholar
Riecke, H. & Paap, H.-G. 1986 Stability and wave-vector restriction of axisymmetric Taylor vortex flow. Phys. Rev. A 33, 547–553.Google Scholar
Rudman, M. 1998 Mixing and particle dispersion in the wavy vortex regime of Taylor–Couette flow. Am. Inst. Chem. Engrs J. 44, 1015–1026.Google Scholar
Schreiber, R. & Keller, H. B. 1983 Driven cavity flows by efficient numerical techniques. J. Comput. Phys. 49, 310–333.CrossRefGoogle Scholar
Schwabe, D., Mizev, A. I., Udhayasankar, M. & Tanaka, S. 2007 Formation of dynamic particle accumulation structures in oscillatory thermocapillary flow in liquid bridges. Phys. Fluids 19, 072102.Google Scholar
Shankar, P. N. & Deshpande, M. D. 2000 Fluid mechanics in the driven cavity. Annu. Rev. Fluid Mech. 32 (1), 93–136.Google Scholar
Shilnikov, L. P. 1965 A case of the existence of a denumerable set of periodic motions. Sov. Math. Dokl. 6, 163–166.Google Scholar
Sotiropoulos, F. & Ventikos, Y. 2001 The three-dimensional structure of confined swirling flows with vortex breakdown. J. Fluid Mech. 426, 155–175.CrossRefGoogle Scholar
Sotiropoulos, F., Ventikos, Y. & Lackey, T. C. 2001 Chaotic advection in three-dimensional stationary vortex-breakdown bubbles: Šil’nikov’s chaos and the devil’s staircase. J. Fluid Mech. 444, 257–297.CrossRefGoogle Scholar
Tiwari, R. K. & Das, M. K. 2007 Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Intl J. Heat Mass Transfer 50, 2002–2018.CrossRefGoogle Scholar
Waleffe, F. 1990 On the three-dimensional instability of strained vortices. Phys. Fluids 2, 76–80.Google Scholar
Xu, B. & Gilchrist, J. F. 2010 Shear migration and chaotic mixing of particle suspensions in a time-periodic lid-driven cavity. Phys. Fluids 22 (5), 053301.Google Scholar