Hostname: page-component-8448b6f56d-mp689 Total loading time: 0 Render date: 2024-04-19T04:57:31.969Z Has data issue: false hasContentIssue false
  • English
  • Français

Transient growth in linearly stable Taylor–Couette flows

Published online by Cambridge University Press:  21 February 2014

Simon Maretzke ,
Björn Hof  and
Marc Avila
Simon Maretzke*
Affiliation:
Faculty of Physics, University of Göttingen, 37073 Göttingen, Germany
Björn Hof
Affiliation:
Max Planck Institute for Dynamics and Self-Organization (MPIDS), 37077 Göttingen, Germany
Marc Avila
Affiliation:
Institute of Fluid Mechanics, Friedrich-Alexander-Universität Erlangen-Nürnberg, 91058 Erlangen, Germany
*
†Email address for correspondence: simon.maretzke@googlemail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Non-normal transient growth of disturbances is considered as an essential prerequisite for subcritical transition in shear flows, i.e. transition to turbulence despite linear stability of the laminar flow. In this work we present numerical and analytical computations of linear transient growth covering all linearly stable regimes of Taylor–Couette flow. Our numerical experiments reveal comparable energy amplifications in the different regimes. 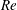For high shear Reynolds numbers $\mathit{Re}$, the optimal transient energy growth always follows a 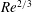$\mathit{Re}^{2/3}$ scaling, which allows for large amplifications even in regimes where the presence of turbulence remains debated. In co-rotating Rayleigh-stable flows, the optimal perturbations become increasingly columnar in their structure, as the optimal axial wavenumber goes to zero. In this limit of axially invariant perturbations, we show that linear stability and transient growth are independent of the cylinder rotation ratio and we derive a universal 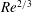$\mathit{Re}^{2/3}$ scaling of optimal energy growth using Wentzel–Kramers–Brillouin theory. Based on this, a semi-empirical formula for the estimation of linear transient growth valid in all regimes is obtained.

JFM classification

Instability: Instability Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 742 , 10 March 2014 , pp. 254 - 290
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

̄eferences

Avila, K. & Hof, B. 2013 High-precision Taylor–Couette experiment to study subcritical transitions and the role of boundary conditions and size effects. Rev. Sci. Instrum. 82 (2), 025105.Google Scholar
Avila, M. 2012 Stability and angular-momentum transport of fluid flows between corotating cylinders. Phys. Rev. Lett. 108, 124501.CrossRefGoogle ScholarPubMed
Balbus, S. A. 2011 Fluid dynamics: a turbulent matter. Nature 470, 475–476.Google Scholar
Boberg, L. & Brosa, U. 1988 Onset of turbulence in a pipe. Z. Naturforsch. 43a, 697–726.Google Scholar
Borrero-Echeverry, D., Schatz, M. F. & Tagg, R. 2010 Transient turbulence in Taylor–Couette flow. Phys. Rev. E (Rapid Communications) 81, 025301.Google Scholar
Burin, M. J. & Czarnocki, C. J. 2012 Subcritical transition and spiral turbulence in circular Couette flow. J. Fluid Mech. 709, 106–122.CrossRefGoogle Scholar
Busse, F. H. 2007 Bounds on the momentum transport by turbulent shear flow in rotating systems. J. Fluid Mech. 583, 303–311.Google Scholar
Canuto, C., Quarteroni, A., Hussaini, M. Y. & Zang, T. A. Jr 2006 Spectral Methods – Fundamentals in Single Domains. 1st edn. Springer.Google Scholar
Chapman, S. J. 2002 Subcritical transition in channel flows. J. Fluid Mech. 451, 35–97.Google Scholar
Coles, D. 1965 Transition in circular Couette flow. J. Fluid Mech. 21, 385–425.Google Scholar
Davey, A. 1973 On the stability of plane Couette flow to infinitesimal disturbances. J. Fluid Mech. 57, 369–380.Google Scholar
DiPrima, R. C. & Habetler, G. J. 1969 A completeness theorem for non-selfadjoint eigenvalue problems in hydrodynamic stability. Arch. Rat. Mech. Anal. 34 (3), 218–227.Google Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Dubrulle, B., Dauchot, O., Daviaud, F., Longaretti, P.-Y., Richard, D. & Zahn, J.-P. 2005 Stability and turbulent transport in Taylor–Couette flow from analysis of experimental data. Phys. Fluids 17 (9), 095103.Google Scholar
Farrell, B. F. 1988 Optimal excitation of perturbations in viscous shear flow. Phys. Fluids 31, 2093–2102.Google Scholar
Gallet, B., Doering, C. R. & Spiegel, E. A. 2010 Destabilizing Taylor–Couette flow with suction. Phys. Fluids 22, 034105.CrossRefGoogle Scholar
Gebhardt, T. & Grossmann, S. 1993 The Taylor–Couette eigenvalue problem with independently rotating cylinders. J. Phys.: Condens. Matter 90, 475–490.Google Scholar
Grossmann, S. 2000 The onset of shear flow turbulence. Rev. Mod. Phys. 72, 603–618.CrossRefGoogle Scholar
Hristova, H., Roch, S., Schmid, P. J. & Tuckerman, L. S. 2002 Transient growth in Taylor–Couette flow. Phys. Fluids 14 (10), 3475–3484.Google Scholar
Ji, H., Burin, M., Schartman, E. & Goodman, J. 2006 Hydrodynamic turbulence cannot transport angular momentum effectively in astrophysical disks. Nature 444, 343–346.Google Scholar
Kato, T. 1995 Perturbation Theory for Linear Operators. 2nd edn. Springer.Google Scholar
Krueger, E. R., Gross, A. & DiPrima, R. C. 1966 On the relative importance of Taylor-vortex and non-axisymmetric modes in flow between rotating cylinders. J. Fluid Mech. 24 (3), 521–538.Google Scholar
Langford, W. F., Tagg, R., Kostelich, E. J., Swinney, H. L. & Golubitsky, M. 1988 Primary instabilities and bicriticality in flow between counter-rotating cylinders. Phys. Fluids 31 (4), 776–785.Google Scholar
Mallock, A. 1896 Experiments on fluid viscosity. Proc. R. Soc. Lond. A 45, 126–132.Google Scholar
Meseguer, A. 2002 Energy transient growth in the Taylor–Couette problem. Phys. Fluids 14 (5), 1655–1660.CrossRefGoogle Scholar
Meseguer, A., Avila, M., Mellibovsky, F. & Marques, F. 2007 Solenoidal spectral formulations for the computation of secondary flows in cylindrical and annular geometries. Eur. Phys. J., Special Topics 146, 249–259.CrossRefGoogle Scholar
Meseguer, A. & Marques, F. 2000 On the competition between centrifugal and shear instability in spiral Couette flow. J. Fluid Mech. 402, 33–56.Google Scholar
Monokrousos, A., Bottaro, A., Brandt, L., Di Vita, A. & Henningson, D. S. 2011 Nonequilibrium thermodynamics and the optimal path to turbulence in shear flows. Phys. Rev. Lett. 106 (13), 134502.Google Scholar
Ogita, T. & Oishi, S. 2012 Accurate and robust inverse Cholesky factorization. Nonlinear Theory Appl. 34 (1), 103–111.Google Scholar
Paoletti, M. S. & Lathrop, D. P. 2011 Angular momentum transport in turbulent flow between independently rotating cylinders. Phys. Rev. Lett. 106, 024501.Google Scholar
Press, W. H., Teukolsky, S. A., Vetterling, W. T. & Flannery, B. P. 2007 Numerical Recipes: The Art of Scientific Computing. 2nd edn. Cambridge University Press.Google Scholar
Pringle, C. C. T. & Kerswell, R. R. 2010 Using nonlinear transient growth to construct the minimal seed for shear flow turbulence. Phys. Rev. Lett. 105 (15), 154502.CrossRefGoogle ScholarPubMed
Pringle, C. C. T., Willis, A. P. & Kerswell, R. R. 2012 Minimal seeds for shear flow turbulence: using nonlinear transient growth to touch the edge of chaos. J. Fluid Mech. 702, 415–443.Google Scholar
Pringle, J. E. 1981 Accretion discs in astrophysics. Annu. Rev. Astron. Astrophys. 19, 137–162.CrossRefGoogle Scholar
Rayleigh, Lord 1917 On the dynamics of revolving fluids. Phil. Trans. R. Soc. Lond. 93, 148–154.Google Scholar
Reddy, S. C. & Henningson, D. S. 1993 Energy growth in viscous channel flows. J. Fluid Mech. 252, 209–238.Google Scholar
Romanov, V. A. 1973 Stability of plane-parallel Couette flow. Funct. Anal. Applics. 7, 137–146.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Applied Mathematical Science, vol. 142. Springer.Google Scholar
Taylor, G. I. 1923 Stability of a viscous liquid contained between two rotating cylinders. Phil. Trans. R. Soc. Lond. 223, 289–343.Google Scholar
Taylor, G. I. 1936 Fluid friction between rotating cylinders. I – Torque measurements. Phil. Trans. R. Soc. Lond. 157 (892), 546–564.Google Scholar
Trefethen, L. N., Trefethen, A. E., Reddy, S. C. & Driscoll, T. A. 1993 Hydrodynamic stability without eigenvalues. Science 261, 578–584.Google Scholar
Wendt, F. 1933 Turbulente Strömungen zwischen zwei rotierenden konaxialen Zylindern. Ing.-Arch. 4, 577–595.Google Scholar
Yecko, P. A. 2004 Accretion disk instability revisited. Astron. Astrophys. 425, 385–393.CrossRefGoogle Scholar