1. Introduction
Rotating convection serves as a fundamental paradigm in fluid dynamics, where the interplay between buoyancy-driven flow and rotation gives rise to intricate patterns and behaviours. This phenomenon is relevant across a wide range of natural and engineering systems, including atmospheric and oceanic circulation (Atkinson & Zhang Reference Atkinson and Zhang1996; Marshall & Schott Reference Marshall and Schott1999), as well as the dynamics of planetary interiors (Aurnou et al. Reference Aurnou, Calkins, Cheng, Julien, King, Nieves, Soderlund and Stellmach2015; Wicht & Sanchez Reference Wicht and Sanchez2019). In engineering applications, it plays a critical role in rotating machinery cooling systems, industrial heat exchangers and chemical reactors, where efficient thermal management is essential (Incropera & DeWitt Reference Incropera and DeWitt1996). Among the various manifestations of rotating convection, rotating Rayleigh–Bénard (RRB) convection (Plumley & Julien Reference Plumley and Julien2019; Kunnen Reference Kunnen2021; Ecke & Shishkina Reference Ecke and Shishkina2023) occupies a central position, representing a canonical example that integrates buoyancy-driven flow with rotation. In the RRB convection configuration, a horizontal layer of fluid is confined between a heated bottom plate and a cooled top plate, subjected to constant rotation aligned with gravity. The three main control parameters of RRB convection are the Rayleigh number
![]() $ Ra \equiv \alpha _T g L^3 \Delta / (\nu \kappa )$
, the Ekman number
$ Ra \equiv \alpha _T g L^3 \Delta / (\nu \kappa )$
, the Ekman number
![]() $ Ek \equiv \nu / (2\Omega L^2)$
, and the Prandtl number
$ Ek \equiv \nu / (2\Omega L^2)$
, and the Prandtl number
![]() $ Pr \equiv \nu / \kappa$
, where
$ Pr \equiv \nu / \kappa$
, where
![]() $ \alpha _T$
is the thermal expansion coefficient,
$ \alpha _T$
is the thermal expansion coefficient,
![]() $ g$
is the gravitational acceleration,
$ g$
is the gravitational acceleration,
![]() $ L$
is the distance between the top and bottom plates,
$ L$
is the distance between the top and bottom plates,
![]() $ \varDelta$
is the temperature difference across the domain,
$ \varDelta$
is the temperature difference across the domain,
![]() $ \nu$
is the kinematic viscosity,
$ \nu$
is the kinematic viscosity,
![]() $ \kappa$
is the thermal diffusivity, and
$ \kappa$
is the thermal diffusivity, and
![]() $ \Omega$
is the rotation rate. The primary system response in this set-up is the Nusselt number (
$ \Omega$
is the rotation rate. The primary system response in this set-up is the Nusselt number (
![]() $Nu$
), which is calculated as
$Nu$
), which is calculated as
![]() $ Nu = \sqrt {Ra\, Pr}\, \langle u_z \theta \rangle _{A,t} - \langle \partial _z \theta \rangle _{A,t}$
, where
$ Nu = \sqrt {Ra\, Pr}\, \langle u_z \theta \rangle _{A,t} - \langle \partial _z \theta \rangle _{A,t}$
, where
![]() $ u_z$
is the vertical velocity,
$ u_z$
is the vertical velocity,
![]() $ \theta$
is the temperature, and
$ \theta$
is the temperature, and
![]() $ \langle \,{\boldsymbol{\cdot}}\, \rangle _{A,t}$
denotes a horizontal and temporal average. Here,
$ \langle \,{\boldsymbol{\cdot}}\, \rangle _{A,t}$
denotes a horizontal and temporal average. Here,
![]() $ u_z$
and
$ u_z$
and
![]() $ \theta$
are scaled using the free-fall velocity
$ \theta$
are scaled using the free-fall velocity
![]() $\sqrt {\alpha _T g L \Delta }$
and
$\sqrt {\alpha _T g L \Delta }$
and
![]() $\varDelta$
. Alternatively, the Nusselt number can be written in its equivalent dimensional form as
$\varDelta$
. Alternatively, the Nusselt number can be written in its equivalent dimensional form as
![]() $Nu = qL / \kappa \Delta$
, where
$Nu = qL / \kappa \Delta$
, where
![]() $q$
is the total heat flux. In recent years, major efforts have been made, both experimentally and numerically, to approach regimes closer to those of planetary interest, where the control parameters are often extreme (van Kan et al. Reference van Kan, Julien, Miquel and Knobloch2024). For example, in the Earth’s fluid core,
$q$
is the total heat flux. In recent years, major efforts have been made, both experimentally and numerically, to approach regimes closer to those of planetary interest, where the control parameters are often extreme (van Kan et al. Reference van Kan, Julien, Miquel and Knobloch2024). For example, in the Earth’s fluid core,
![]() $ Ek \approx 10^{-15}$
and
$ Ek \approx 10^{-15}$
and
![]() $ Ra \approx 10^{29}$
(Gubbins Reference Gubbins2001; Guervilly, Cardin & Schaeffer Reference Guervilly, Cardin and Schaeffer2019).
$ Ra \approx 10^{29}$
(Gubbins Reference Gubbins2001; Guervilly, Cardin & Schaeffer Reference Guervilly, Cardin and Schaeffer2019).
A key aspect of RRB convection research is understanding how
![]() $Nu$
scales with the control parameters. For a comprehensive overview of RRBconvection, including the key scaling laws for
$Nu$
scales with the control parameters. For a comprehensive overview of RRBconvection, including the key scaling laws for
![]() $Nu$
as a function of control parameters, we refer to the recent reviews by Plumley & Julien (Reference Plumley and Julien2019), Kunnen (Reference Kunnen2021)and Ecke & Shishkina (Reference Ecke and Shishkina2023). Specifically, for no-slip boundary conditions and fixed
$Nu$
as a function of control parameters, we refer to the recent reviews by Plumley & Julien (Reference Plumley and Julien2019), Kunnen (Reference Kunnen2021)and Ecke & Shishkina (Reference Ecke and Shishkina2023). Specifically, for no-slip boundary conditions and fixed
![]() $Ek$
,
$Ek$
,
![]() $Nu$
increases steeply with
$Nu$
increases steeply with
![]() $Ra$
from its value unity at the onset of convection towards a shallower scaling typical of the non-rotating case. In the steep scaling regime, rotation dominates, and the Coriolis force balances the pressure gradient, a condition known as geostrophic balance (Greenspan Reference Greenspan1969). In this rotation-dominated regime, the heat transfer scaling follows
$Ra$
from its value unity at the onset of convection towards a shallower scaling typical of the non-rotating case. In the steep scaling regime, rotation dominates, and the Coriolis force balances the pressure gradient, a condition known as geostrophic balance (Greenspan Reference Greenspan1969). In this rotation-dominated regime, the heat transfer scaling follows
![]() $ Nu \sim (Ra / Ra_c)^{\xi } \sim (Ra \, Ek^{4/3})^{\xi }$
, where
$ Nu \sim (Ra / Ra_c)^{\xi } \sim (Ra \, Ek^{4/3})^{\xi }$
, where
![]() $ Ra_c \sim Ek^{-4/3}$
is the critical Rayleigh number for the onset of convection with rotation (Chandrasekhar Reference Chandrasekhar1961; Julien et al. Reference Julien, Rubio, Grooms and Knobloch2012b
; Stellmach et al. Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014). The significant effect of Ekman pumping in no-slip boundaries can lead to a very steep scaling relation
$ Ra_c \sim Ek^{-4/3}$
is the critical Rayleigh number for the onset of convection with rotation (Chandrasekhar Reference Chandrasekhar1961; Julien et al. Reference Julien, Rubio, Grooms and Knobloch2012b
; Stellmach et al. Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014). The significant effect of Ekman pumping in no-slip boundaries can lead to a very steep scaling relation
![]() $ Nu \sim Ra^{3.6} Ek^{4.8}$
(Cheng et al. Reference Cheng, Stellmach, Ribeiro, Grannan, King and Aurnou2015), when
$ Nu \sim Ra^{3.6} Ek^{4.8}$
(Cheng et al. Reference Cheng, Stellmach, Ribeiro, Grannan, King and Aurnou2015), when
![]() $ Pr = 7$
. Cheng et al. (Reference Cheng, Stellmach, Ribeiro, Grannan, King and Aurnou2015) report a very steep scaling for the heat transport in rotating convection, expressed as
$ Pr = 7$
. Cheng et al. (Reference Cheng, Stellmach, Ribeiro, Grannan, King and Aurnou2015) report a very steep scaling for the heat transport in rotating convection, expressed as
![]() $Nu \sim (Ra\,Ek^{4/3})^\xi$
. Crucially, their main finding is that the scaling exponent
$Nu \sim (Ra\,Ek^{4/3})^\xi$
. Crucially, their main finding is that the scaling exponent
![]() $\xi$
is dependent on the Ekman number; specifically, as
$\xi$
is dependent on the Ekman number; specifically, as
![]() $Ek$
decreases,
$Ek$
decreases,
![]() $\xi$
increases, indicating a steeper heat transport scaling under more rapid rotation. Theoretically, in extreme parameter regimes, a diffusion-free heat transport scaling
$\xi$
increases, indicating a steeper heat transport scaling under more rapid rotation. Theoretically, in extreme parameter regimes, a diffusion-free heat transport scaling
![]() $ Nu \sim Ra^{3/2} Ek^2 Pr^{-1/2}$
(Gillet & Jones Reference Gillet and Jones2006; Julien et al. Reference Julien, Knobloch, Rubio and Vasil2012a
), analogous to the asymptotic ultimate regime
$ Nu \sim Ra^{3/2} Ek^2 Pr^{-1/2}$
(Gillet & Jones Reference Gillet and Jones2006; Julien et al. Reference Julien, Knobloch, Rubio and Vasil2012a
), analogous to the asymptotic ultimate regime
![]() $ Nu \sim Ra^{1/2} Pr^{1/2}$
in non-rotating Rayleigh–Bénard convection (Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009; Lohse & Shishkina Reference Lohse and Shishkina2024), is expected in the geostrophic turbulent regime. Recently, this scaling has been observed with no-slip boundaries at very high
$ Nu \sim Ra^{1/2} Pr^{1/2}$
in non-rotating Rayleigh–Bénard convection (Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009; Lohse & Shishkina Reference Lohse and Shishkina2024), is expected in the geostrophic turbulent regime. Recently, this scaling has been observed with no-slip boundaries at very high
![]() $ Ra \gtrsim 10^{12}$
and very strong rotation
$ Ra \gtrsim 10^{12}$
and very strong rotation
![]() $ Ek \lesssim 10^{-8}$
(Song, Shishkina & Zhu Reference Song, Shishkina and Zhu2024b
,Reference Song, Shishkina and Zhu
c
).
$ Ek \lesssim 10^{-8}$
(Song, Shishkina & Zhu Reference Song, Shishkina and Zhu2024b
,Reference Song, Shishkina and Zhu
c
).
Beyond the rotation-dominated regime, as the thermal driving force increases, the flow transitions into a rotation-affected regime. This regime, which marks the boundary between rotation-dominated and buoyancy-dominated regimes, has garnered considerable attention (Kunnen Reference Kunnen2021; Ecke & Shishkina Reference Ecke and Shishkina2023). It is suggested that this transition occurs when the thermal and Ekman boundary layer thicknesses become comparable, with the transitional Rayleigh number
![]() $Ra_T$
between the two regimes following the relation
$Ra_T$
between the two regimes following the relation
![]() $ Ra_T \sim Ek^{-7/4}$
(King et al. Reference King, Stellmach, Noir, Hansen and Aurnou2009), which is derived from
$ Ra_T \sim Ek^{-7/4}$
(King et al. Reference King, Stellmach, Noir, Hansen and Aurnou2009), which is derived from
![]() $ \delta _\theta \sim Nu^{-1} \sim Ra^{-2/7} \sim \delta _E \sim Ek^{1/2}$
, where
$ \delta _\theta \sim Nu^{-1} \sim Ra^{-2/7} \sim \delta _E \sim Ek^{1/2}$
, where
![]() $ \delta _\theta$
represents the thermal boundary layer thickness,
$ \delta _\theta$
represents the thermal boundary layer thickness,
![]() $ Ra^{-2/7}$
indicates the
$ Ra^{-2/7}$
indicates the
![]() $Nu$
scaling for non-rotating convection, and
$Nu$
scaling for non-rotating convection, and
![]() $ \delta _E$
is the Ekman layer thickness. This scaling was later refined to
$ \delta _E$
is the Ekman layer thickness. This scaling was later refined to
![]() $ Ra_T \sim Ek^{-3/2}$
(King, Stellmach & Aurnou Reference King, Stellmach and Aurnou2012), based on the assumption that
$ Ra_T \sim Ek^{-3/2}$
(King, Stellmach & Aurnou Reference King, Stellmach and Aurnou2012), based on the assumption that
![]() $ Nu \sim Ra^{1/3}$
instead of
$ Nu \sim Ra^{1/3}$
instead of
![]() $ Nu \sim Ra^{2/7}$
. This transitional scaling has been validated across various datasets under different conditions (Cheng et al. Reference Cheng, Stellmach, Ribeiro, Grannan, King and Aurnou2015; Kunnen Reference Kunnen2021; Ecke & Shishkina Reference Ecke and Shishkina2023; Song et al. Reference Song, Kannan, Shishkina and Zhu2024a
).
$ Nu \sim Ra^{2/7}$
. This transitional scaling has been validated across various datasets under different conditions (Cheng et al. Reference Cheng, Stellmach, Ribeiro, Grannan, King and Aurnou2015; Kunnen Reference Kunnen2021; Ecke & Shishkina Reference Ecke and Shishkina2023; Song et al. Reference Song, Kannan, Shishkina and Zhu2024a
).
The transition from the rotation-dominated to the buoyancy-dominated regime is a fundamental aspect of rotating convection. Previous investigations have focused primarily on cases with no-slip boundary conditions, where the transition is thought to be governed by Ekman boundary layer dynamics. However, this transition is equally significant in systems with stress-free boundary conditions (Stellmach et al. Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014; Kunnen et al. Reference Kunnen, Ostilla-Mónico, van der Poel, Verzicco and Lohse2016; Plumley et al. Reference Plumley, Julien, Marti and Stellmach2017; Maffei et al. Reference Maffei, Krouss, Julien and Calkins2021) and in homogeneous convection without boundaries (Toselli, Musacchio & Boffetta Reference Toselli, Musacchio and Boffetta2019), where Ekman boundary layers are absent. Note that the study utilizing an asymptotic/quasi-geostrophic model (e.g. Maffei et al. Reference Maffei, Krouss, Julien and Calkins2021), which assumes rapid rotation, is not designed to capture the full transitional dynamics observed in direct numerical simulations (DNS) formulations. These simplified set-ups – stress-free boundaries and homogeneous convection – provide valuable models for studying rotating fluids in geophysical and astrophysical contexts. In this context, the theory proposed by Cheng et al. (Reference Cheng, Stellmach, Ribeiro, Grannan, King and Aurnou2015) is appealing because it does not involve Ekman layers. The theory empirically defines
![]() $ Ra_T$
as the intersection between two heat transfer scaling laws: the steep scaling
$ Ra_T$
as the intersection between two heat transfer scaling laws: the steep scaling
![]() $ Nu \sim (Ra / Ra_c)^\xi$
, typical for rapidly rotating convection, and the shallow non-rotating scaling
$ Nu \sim (Ra / Ra_c)^\xi$
, typical for rapidly rotating convection, and the shallow non-rotating scaling
![]() $ Nu \sim Ra^\alpha$
. By equating these trends, the transition is predicted as
$ Nu \sim Ra^\alpha$
. By equating these trends, the transition is predicted as
![]() $ Ra_T \sim Ek^{-4\xi / 3(\xi - \alpha )}$
. Using
$ Ra_T \sim Ek^{-4\xi / 3(\xi - \alpha )}$
. Using
![]() $ \xi = 3$
, the characteristic scaling exponent in rapidly rotating convection with no-slip boundaries (King et al. Reference King, Stellmach and Aurnou2012; Song et al. Reference Song, Shishkina and Zhu2024c
), and
$ \xi = 3$
, the characteristic scaling exponent in rapidly rotating convection with no-slip boundaries (King et al. Reference King, Stellmach and Aurnou2012; Song et al. Reference Song, Shishkina and Zhu2024c
), and
![]() $ \alpha = 1/3$
, the typical exponent for non-rotating Rayleigh–Bénard convection in the classical regime (Malkus Reference Malkus1954; Ahlers et al. Reference Ahlers, Grossmann and Lohse2009), Cheng et al. (Reference Cheng, Stellmach, Ribeiro, Grannan, King and Aurnou2015) derived
$ \alpha = 1/3$
, the typical exponent for non-rotating Rayleigh–Bénard convection in the classical regime (Malkus Reference Malkus1954; Ahlers et al. Reference Ahlers, Grossmann and Lohse2009), Cheng et al. (Reference Cheng, Stellmach, Ribeiro, Grannan, King and Aurnou2015) derived
![]() $ Ra_T \sim Ek^{-3/2}$
as well. Motivated by this framework, we employ DNS to study the transition under stress-free boundary conditions, and incorporate data from homogeneous rotating convection provided by Toselli et al. (Reference Toselli, Musacchio and Boffetta2019). Beyond investigating the transition through
$ Ra_T \sim Ek^{-3/2}$
as well. Motivated by this framework, we employ DNS to study the transition under stress-free boundary conditions, and incorporate data from homogeneous rotating convection provided by Toselli et al. (Reference Toselli, Musacchio and Boffetta2019). Beyond investigating the transition through
![]() $ Nu$
, we also show that the transition can be characterized and predicted using the Reynolds number (
$ Nu$
, we also show that the transition can be characterized and predicted using the Reynolds number (
![]() $ Re = u L / \nu$
), where
$ Re = u L / \nu$
), where
![]() $ u$
is the root mean square velocity. This additional system response offers further confirmation of the same transitional behaviour.
$ u$
is the root mean square velocity. This additional system response offers further confirmation of the same transitional behaviour.
2. Numerical details
The current DNS employ the Boussinesq approximation to model RRB convection in a fluid confined between two horizontal plates. The system is subjected to a constant angular velocity
![]() $\Omega$
around the vertical axis
$\Omega$
around the vertical axis
![]() $z$
, with gravitational acceleration
$z$
, with gravitational acceleration
![]() $\boldsymbol{g}=-g\boldsymbol{e}_z$
, where
$\boldsymbol{g}=-g\boldsymbol{e}_z$
, where
![]() $\boldsymbol{e}_z$
is the unit vector in the vertical direction. The reference scales used in this study are the height of the domain
$\boldsymbol{e}_z$
is the unit vector in the vertical direction. The reference scales used in this study are the height of the domain
![]() $L$
, the temperature difference between the plates
$L$
, the temperature difference between the plates
![]() $\varDelta$
, and the characteristic free-fall velocity
$\varDelta$
, and the characteristic free-fall velocity
![]() $U_{ff}=\sqrt {\alpha _T g L \Delta }$
. The dimensionless variables for temperature
$U_{ff}=\sqrt {\alpha _T g L \Delta }$
. The dimensionless variables for temperature
![]() $\theta$
, velocity
$\theta$
, velocity
![]() $\boldsymbol{u}$
, pressure
$\boldsymbol{u}$
, pressure
![]() $p$
, and time
$p$
, and time
![]() $t$
are defined based on these scales. The resulting dimensionless governing equations for the incompressible fluid flow are
$t$
are defined based on these scales. The resulting dimensionless governing equations for the incompressible fluid flow are
To solve the governing equations, the energy-conserving second-order finite-difference code AFiD was employed (Verzicco & Orlandi Reference Verzicco and Orlandi1996; van der Poel et al. Reference van der Poel, Ostilla-Mónico, Donners and Verzicco2015; Zhu et al. Reference Zhu2018). The code was parallelized using a two-dimensional pencil domain decomposition strategy (van der Poel et al. Reference van der Poel, Ostilla-Mónico, Donners and Verzicco2015) and GPU acceleration (Zhu et al. Reference Zhu2018) for large-scale DNS. The simulations applied stress-free boundary conditions with a constant temperature at the top and bottom plates, along with periodic boundary conditions in both horizontal directions.
The grid points were distributed using a Chebyshev-like scheme in the wall-normal (
![]() $z$
) direction, clustering points near the top and bottom plates, while a uniform distribution was used in the periodic (
$z$
) direction, clustering points near the top and bottom plates, while a uniform distribution was used in the periodic (
![]() $x$
and
$x$
and
![]() $y$
) directions. This arrangement ensures that at least 10 grid points are always present within the thermal boundary layer.
$y$
) directions. This arrangement ensures that at least 10 grid points are always present within the thermal boundary layer.
Additionally, to assess the grid resolution used in the DNS, we calculated the mean dimensionless Kolmogorov microscale, defined as
![]() $\eta / L = (\tilde {\nu }^3 / \langle \tilde {\epsilon } \rangle _V)^{1/4}$
, where
$\eta / L = (\tilde {\nu }^3 / \langle \tilde {\epsilon } \rangle _V)^{1/4}$
, where
![]() $\tilde {\nu } = \sqrt {{Pr}/{Ra}}$
is the dimensionless viscosity, and
$\tilde {\nu } = \sqrt {{Pr}/{Ra}}$
is the dimensionless viscosity, and
![]() $\langle \tilde {\epsilon } \rangle _V$
is the volume- and time-averaged dimensionless kinetic energy dissipation rate. The maximum ratio of the mesh size to the mean Kolmogorov microscale remains below
$\langle \tilde {\epsilon } \rangle _V$
is the volume- and time-averaged dimensionless kinetic energy dissipation rate. The maximum ratio of the mesh size to the mean Kolmogorov microscale remains below
![]() $2.2$
in all simulations, a threshold that has been found empirically to be acceptable in rotating convection simulations (Verzicco & Camussi Reference Verzicco and Camussi2003; Shishkina et al. Reference Shishkina, Stevens, Grossmann and Lohse2010; Scheel, Emran & Schumacher Reference Scheel, Emran and Schumacher2013).
$2.2$
in all simulations, a threshold that has been found empirically to be acceptable in rotating convection simulations (Verzicco & Camussi Reference Verzicco and Camussi2003; Shishkina et al. Reference Shishkina, Stevens, Grossmann and Lohse2010; Scheel, Emran & Schumacher Reference Scheel, Emran and Schumacher2013).
All simulations were performed using
![]() $Pr=1$
and were run long enough to achieve saturation of thermal and kinetic energies, ensuring statistically steady flow states, and allowing the inverse energy cascade to saturate, particularly in cases exhibiting large-scale vortices with no evidence of secular growth. Moreover, ensemble averages were taken over 200 free-fall time units after reaching the saturation state.
$Pr=1$
and were run long enough to achieve saturation of thermal and kinetic energies, ensuring statistically steady flow states, and allowing the inverse energy cascade to saturate, particularly in cases exhibiting large-scale vortices with no evidence of secular growth. Moreover, ensemble averages were taken over 200 free-fall time units after reaching the saturation state.
To ensure accuracy, the convergence of
![]() $Nu$
was thoroughly checked across the entire domain. The maximum relative error in
$Nu$
was thoroughly checked across the entire domain. The maximum relative error in
![]() $Nu$
, calculated using five different methods (as outlined in Stevens, Verzicco & Lohse Reference Stevens, Verzicco and Lohse2010), was kept below 1 %. The explored parameter range, along with the corresponding grid resolution and transport parameters in the present DNS of stress-free RRBconvection, is summarized in Appendix A.
$Nu$
, calculated using five different methods (as outlined in Stevens, Verzicco & Lohse Reference Stevens, Verzicco and Lohse2010), was kept below 1 %. The explored parameter range, along with the corresponding grid resolution and transport parameters in the present DNS of stress-free RRBconvection, is summarized in Appendix A.
Figure 1. Horizontal cross-sections of the instantaneous contours of fluctuating temperature
![]() $\theta$
for stress-free RRB convection at the mid-plane is shown for varying
$\theta$
for stress-free RRB convection at the mid-plane is shown for varying
![]() $Ra$
, with fixed
$Ra$
, with fixed
![]() $Ek = 5 \times 10^{-6}$
and
$Ek = 5 \times 10^{-6}$
and
![]() $Pr = 1$
. Here, red (blue) denotes positive (negative) temperature fluctuations. The nine plots correspond to a range of the supercriticality parameter,
$Pr = 1$
. Here, red (blue) denotes positive (negative) temperature fluctuations. The nine plots correspond to a range of the supercriticality parameter,
![]() $10 \lt \widetilde {Ra} \equiv Ra\,Ek^{4/3} \lt 4275$
.
$10 \lt \widetilde {Ra} \equiv Ra\,Ek^{4/3} \lt 4275$
.
Figure 2. Horizontal cross-sections of the instantaneous contours of vertical vorticity
![]() $\omega _z$
for the same flow conditions as in figure 1. Here, red (blue) denotes positive (negative) vorticity.
$\omega _z$
for the same flow conditions as in figure 1. Here, red (blue) denotes positive (negative) vorticity.
Figure 3. Vertical cross-sections of the instantaneous contours of vertical velocity
![]() $u_z$
for the same flow conditions as in figure 1. Here, red (blue) denotes positive (negative) velocity.
$u_z$
for the same flow conditions as in figure 1. Here, red (blue) denotes positive (negative) velocity.
3. Scalings and flow structures in DNS with stress-free boundaries
Inspection of the mid-plane horizontal cross-section contours of fluctuating temperature (figure 1), vertical vorticity (figure 2) and the vertical cross-section of vertical velocity (figure 3) for varying
![]() $ Ra \in [1.3 \times 10^8, 5 \times 10^{10}]$
at a fixed
$ Ra \in [1.3 \times 10^8, 5 \times 10^{10}]$
at a fixed
![]() $Ek = 5 \times 10^{-6}$
with stress-free boundaries suggests that the flow can be classified qualitatively into several distinct regimes. While some studies adopt a detailed classification that includes cells, Taylor columns, plumes, geostrophic turbulence (where large-scale vortices form), and eventually regimes where rotation becomes negligible, our work focuses primarily on the transition between rotation-dominated and buoyancy-dominated states (Sprague et al. Reference Sprague, Julien, Knobloch and Werne2006; Julien et al. Reference Julien, Rubio, Grooms and Knobloch2012b
). The cellular regime is characterized by columns that extend across the fluid layer, formed due to the dominance of strong rotational effects over buoyancy forces. These cells are encased in ’sleeves’ of cold fluid, which act as insulating layers and limit interaction between adjacent columns. In contrast, the Taylor columns regime, characterized by vertically coherent columnar structures, is typically observed for fluids with
$Ek = 5 \times 10^{-6}$
with stress-free boundaries suggests that the flow can be classified qualitatively into several distinct regimes. While some studies adopt a detailed classification that includes cells, Taylor columns, plumes, geostrophic turbulence (where large-scale vortices form), and eventually regimes where rotation becomes negligible, our work focuses primarily on the transition between rotation-dominated and buoyancy-dominated states (Sprague et al. Reference Sprague, Julien, Knobloch and Werne2006; Julien et al. Reference Julien, Rubio, Grooms and Knobloch2012b
). The cellular regime is characterized by columns that extend across the fluid layer, formed due to the dominance of strong rotational effects over buoyancy forces. These cells are encased in ’sleeves’ of cold fluid, which act as insulating layers and limit interaction between adjacent columns. In contrast, the Taylor columns regime, characterized by vertically coherent columnar structures, is typically observed for fluids with
![]() $Pr\gt 1$
(Julien et al. Reference Julien, Rubio, Grooms and Knobloch2012b
). However, as
$Pr\gt 1$
(Julien et al. Reference Julien, Rubio, Grooms and Knobloch2012b
). However, as
![]() $Ra$
increases, the insulating effect diminishes, leading to greater interaction between the columns. This reduction in column length signals the transition to the large-scale vortex regime, where vortices intensify and occupy the entire domain (Julien et al. Reference Julien, Rubio, Grooms and Knobloch2012b
; Favier, Silvers & Proctor Reference Favier, Silvers and Proctor2014; Guervilly, Hughes & Jones Reference Guervilly, Hughes and Jones2014; Rubio et al. Reference Rubio, Julien, Knobloch and Weiss2014; Favier, Guervilly & Knobloch Reference Favier, Guervilly and Knobloch2019; Aguirre Guzmán et al. Reference Aguirre Guzmán, Madonia, Cheng, Ostilla-Mónico, Clercx and Kunnen2021; Maffei et al. Reference Maffei, Krouss, Julien and Calkins2021; De Wit, Van Kan & Alexakis Reference De Wit, Van Kan and Alexakis2022). As
$Ra$
increases, the insulating effect diminishes, leading to greater interaction between the columns. This reduction in column length signals the transition to the large-scale vortex regime, where vortices intensify and occupy the entire domain (Julien et al. Reference Julien, Rubio, Grooms and Knobloch2012b
; Favier, Silvers & Proctor Reference Favier, Silvers and Proctor2014; Guervilly, Hughes & Jones Reference Guervilly, Hughes and Jones2014; Rubio et al. Reference Rubio, Julien, Knobloch and Weiss2014; Favier, Guervilly & Knobloch Reference Favier, Guervilly and Knobloch2019; Aguirre Guzmán et al. Reference Aguirre Guzmán, Madonia, Cheng, Ostilla-Mónico, Clercx and Kunnen2021; Maffei et al. Reference Maffei, Krouss, Julien and Calkins2021; De Wit, Van Kan & Alexakis Reference De Wit, Van Kan and Alexakis2022). As
![]() $Ra$
continues to rise, the large-scale vortices transition from a cyclone–anticyclone dipole structure to a cyclonic structure within an anticyclonic sheath, which eventually disappears. The flow then transitions to a buoyancy-dominated turbulence regime, where the influence of rotation becomes very weak or negligible, and the flow behaviour aligns with classical non-rotating Rayleigh–Bénard convection.
$Ra$
continues to rise, the large-scale vortices transition from a cyclone–anticyclone dipole structure to a cyclonic structure within an anticyclonic sheath, which eventually disappears. The flow then transitions to a buoyancy-dominated turbulence regime, where the influence of rotation becomes very weak or negligible, and the flow behaviour aligns with classical non-rotating Rayleigh–Bénard convection.
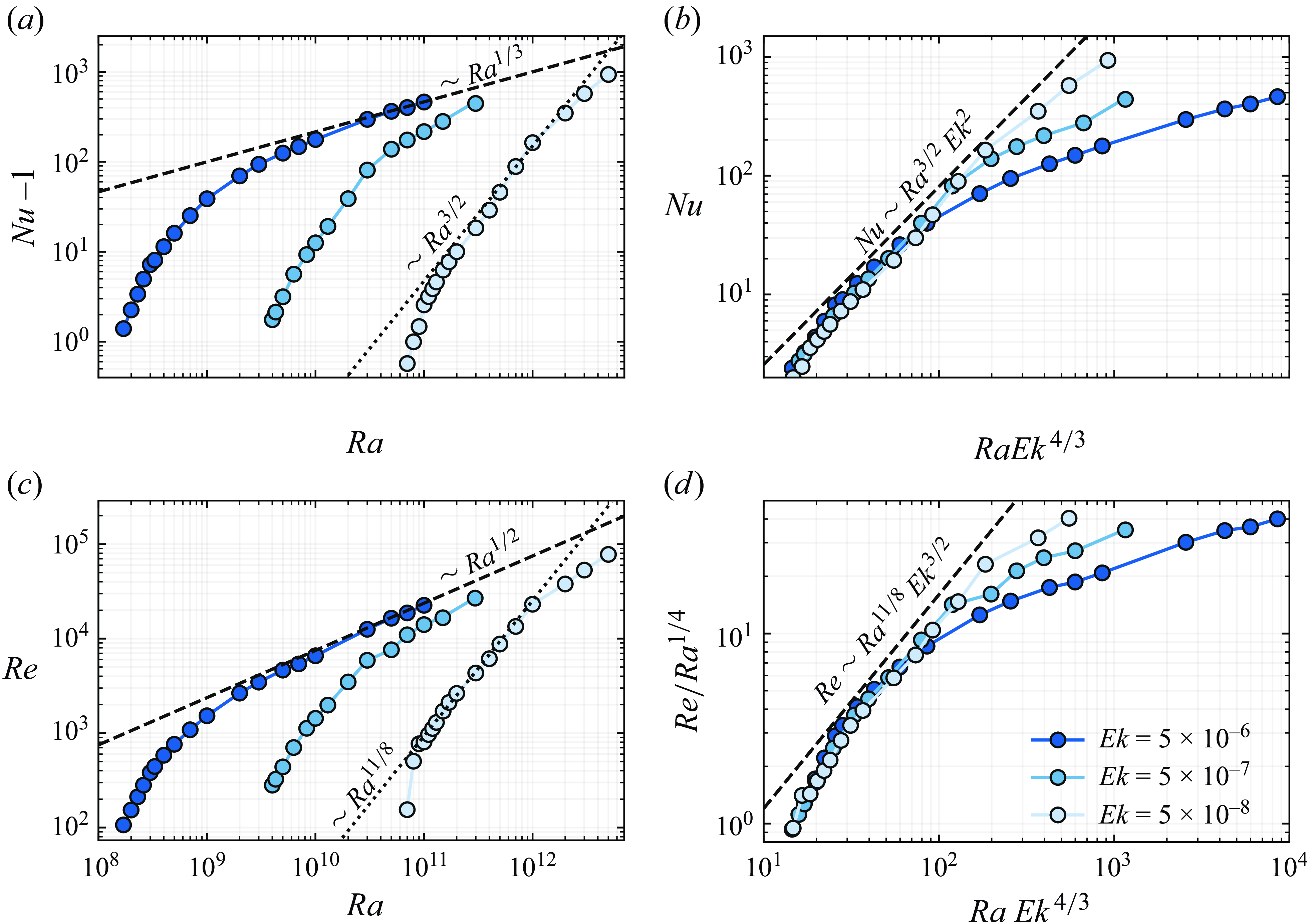
Figure 4. (a) Dimensionless heat transport (
![]() $Nu-1$
) and (c) momentum transport (
$Nu-1$
) and (c) momentum transport (
![]() $Re$
) versus
$Re$
) versus
![]() $Ra$
for various
$Ra$
for various
![]() $Ek$
, obtained from DNS of RRB convection with stress-free boundaries and
$Ek$
, obtained from DNS of RRB convection with stress-free boundaries and
![]() $Pr = 1$
. Black dashed lines show non-rotating convection scalings (
$Pr = 1$
. Black dashed lines show non-rotating convection scalings (
![]() $Nu - 1 \sim Ra^{1/3}$
,
$Nu - 1 \sim Ra^{1/3}$
,
![]() $Re \sim Ra^{1/2}$
), and dotted lines indicate geostrophic turbulence scalings (
$Re \sim Ra^{1/2}$
), and dotted lines indicate geostrophic turbulence scalings (
![]() $Nu - 1 \sim Ra^{3/2}$
,
$Nu - 1 \sim Ra^{3/2}$
,
![]() $Re \sim Ra^{11/8}$
). Plots of (b)
$Re \sim Ra^{11/8}$
). Plots of (b)
![]() $Nu$
and (d)
$Nu$
and (d)
![]() $Re$
, normalized by
$Re$
, normalized by
![]() $Ra^{1/4}$
, as functions of the supercriticality parameter
$Ra^{1/4}$
, as functions of the supercriticality parameter
![]() $Ra\,Ek^{4/3}$
. Dashed lines represent rotation-dominant regime scalings (
$Ra\,Ek^{4/3}$
. Dashed lines represent rotation-dominant regime scalings (
![]() $Nu \sim Ra^{3/2}Ek^{2}$
,
$Nu \sim Ra^{3/2}Ek^{2}$
,
![]() $Re \sim Ra^{11/8}Ek^{3/2}$
). Here, for stress-free cases,
$Re \sim Ra^{11/8}Ek^{3/2}$
). Here, for stress-free cases,
![]() $Re$
is defined based on
$Re$
is defined based on
![]() $u_z$
, as the horizontal velocity is significantly larger than the vertical velocity due to the strong inverse energy cascade. Therefore, the horizontal velocity does not characterize the heat transfer effectively.
$u_z$
, as the horizontal velocity is significantly larger than the vertical velocity due to the strong inverse energy cascade. Therefore, the horizontal velocity does not characterize the heat transfer effectively.
An overview of the characteristics of RRB convection from the beginning of the onset can also be seen in the
![]() $Nu$
measurements, covering a wide range of
$Nu$
measurements, covering a wide range of
![]() $Ra$
and
$Ra$
and
![]() $Ek$
values (see figure 4
a). The rapid rise from the conduction value
$Ek$
values (see figure 4
a). The rapid rise from the conduction value
![]() $Nu = 1$
represents the nonlinear growth from onset and a region of rotation-dominated dynamics at
$Nu = 1$
represents the nonlinear growth from onset and a region of rotation-dominated dynamics at
![]() $Ra \gt Ra_c$
, where
$Ra \gt Ra_c$
, where
![]() $Ra_c$
is the critical Rayleigh number for onset. As demonstrated by these data, the range of
$Ra_c$
is the critical Rayleigh number for onset. As demonstrated by these data, the range of
![]() $Ra$
spanned in this rotation-dominated region increases with decreasing
$Ra$
spanned in this rotation-dominated region increases with decreasing
![]() $Ek$
. The scaling behaviour of
$Ek$
. The scaling behaviour of
![]() $Nu$
in the rotation-dominated regime provides insights into how heat transport is influenced by the interplay of buoyancy and rotational forces. For stress-free boundary conditions, the heat transport follows the scaling
$Nu$
in the rotation-dominated regime provides insights into how heat transport is influenced by the interplay of buoyancy and rotational forces. For stress-free boundary conditions, the heat transport follows the scaling
![]() $Nu \sim Ra^{3/2}Ek^2$
in a wide range in the rotation-dominated regime, as shown in figure 4(b). This scaling is consistent with predictions for the diffusion-free regime, where thermal and momentum transport are not constrained by diffusivity (Stevenson Reference Stevenson1979; Gillet & Jones Reference Gillet and Jones2006; Julien et al. Reference Julien, Knobloch, Rubio and Vasil2012a, Reference Julien, Aurnou, Calkins, Knobloch, Marti, Stellmach and Vasil2016; Stellmach et al. Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014; Cheng & Aurnou Reference Cheng and Aurnou2016; Plumley et al. Reference Plumley, Julien, Marti and Stellmach2017; Bouillauta et al. Reference Bouillauta, Miquela, Julien, Aumaître and Gallet2021; Maffei et al. Reference Maffei, Krouss, Julien and Calkins2021; Oliver et al. Reference Oliver, Jacobi, Julien and Calkins2023; van Kan et al. Reference van Kan, Julien, Miquel and Knobloch2024; Song et al. Reference Song, Shishkina and Zhu2024c
). Notably, the
$Nu \sim Ra^{3/2}Ek^2$
in a wide range in the rotation-dominated regime, as shown in figure 4(b). This scaling is consistent with predictions for the diffusion-free regime, where thermal and momentum transport are not constrained by diffusivity (Stevenson Reference Stevenson1979; Gillet & Jones Reference Gillet and Jones2006; Julien et al. Reference Julien, Knobloch, Rubio and Vasil2012a, Reference Julien, Aurnou, Calkins, Knobloch, Marti, Stellmach and Vasil2016; Stellmach et al. Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014; Cheng & Aurnou Reference Cheng and Aurnou2016; Plumley et al. Reference Plumley, Julien, Marti and Stellmach2017; Bouillauta et al. Reference Bouillauta, Miquela, Julien, Aumaître and Gallet2021; Maffei et al. Reference Maffei, Krouss, Julien and Calkins2021; Oliver et al. Reference Oliver, Jacobi, Julien and Calkins2023; van Kan et al. Reference van Kan, Julien, Miquel and Knobloch2024; Song et al. Reference Song, Shishkina and Zhu2024c
). Notably, the
![]() $3/2$
scaling in the stress-free case can be observed at relatively high
$3/2$
scaling in the stress-free case can be observed at relatively high
![]() $Ek$
(
$Ek$
(
![]() $Ek=5\times 10^{-7}$
) (Julien et al. Reference Julien, Knobloch, Rubio and Vasil2012a
; Stellmach et al. Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014; Plumley et al. Reference Plumley, Julien, Marti and Stellmach2017), in contrast to the no-slip boundary condition cases, where the
$Ek=5\times 10^{-7}$
) (Julien et al. Reference Julien, Knobloch, Rubio and Vasil2012a
; Stellmach et al. Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014; Plumley et al. Reference Plumley, Julien, Marti and Stellmach2017), in contrast to the no-slip boundary condition cases, where the
![]() $3/2$
scaling is limited to extremely low
$3/2$
scaling is limited to extremely low
![]() $Ek$
(
$Ek$
(
![]() $Ek=5\times 10^{-9}$
) (Song et al. Reference Song, Shishkina and Zhu2024c
). As
$Ek=5\times 10^{-9}$
) (Song et al. Reference Song, Shishkina and Zhu2024c
). As
![]() $Ra$
increases further at constant
$Ra$
increases further at constant
![]() $Ek$
, the balance of rotation and buoyancy shifts, such that
$Ek$
, the balance of rotation and buoyancy shifts, such that
![]() $Nu$
approaches the non-rotating convection curve
$Nu$
approaches the non-rotating convection curve
![]() $Nu \sim Ra^{1/3}$
, the so-called classical regime (Ahlers et al. Reference Ahlers, Grossmann and Lohse2009; Lohse & Shishkina Reference Lohse and Shishkina2024). Note that the scaling observed in non-rotating Rayleigh–Bénard convection with stress-free boundary conditions is comparable to that with no-slip boundary conditions (Petschel et al. Reference Petschel, Stellmach, Wilczek, Lülff and Hansen2013).
$Nu \sim Ra^{1/3}$
, the so-called classical regime (Ahlers et al. Reference Ahlers, Grossmann and Lohse2009; Lohse & Shishkina Reference Lohse and Shishkina2024). Note that the scaling observed in non-rotating Rayleigh–Bénard convection with stress-free boundary conditions is comparable to that with no-slip boundary conditions (Petschel et al. Reference Petschel, Stellmach, Wilczek, Lülff and Hansen2013).
Within the studied parameter regime – where the dynamics is governed by a balance between the Coriolis force and buoyancy – the Nusselt number exhibits a scaling transition from
![]() $Ra^{3/2}$
to
$Ra^{3/2}$
to
![]() $Ra^{1/3}$
. This behaviour aligns with theoretical predictions and previous experimental and numerical studies (Ahlers et al. Reference Ahlers, Grossmann and Lohse2009; Julien et al. Reference Julien, Knobloch, Rubio and Vasil2012b
; Cheng et al. Reference Cheng, Stellmach, Ribeiro, Grannan, King and Aurnou2015). Although the
$Ra^{1/3}$
. This behaviour aligns with theoretical predictions and previous experimental and numerical studies (Ahlers et al. Reference Ahlers, Grossmann and Lohse2009; Julien et al. Reference Julien, Knobloch, Rubio and Vasil2012b
; Cheng et al. Reference Cheng, Stellmach, Ribeiro, Grannan, King and Aurnou2015). Although the
![]() $Ra^{3/2}$
scaling is often interpreted as indicative of a diffusion-free regime, our analysis reveals that other dynamics remain influenced by diffusive processes. This is evidenced by a Reynolds number scaling (see discussion below) that deviates from the diffusion-free expectation. Hence the observed transition does not signify a complete shift from a truly diffusion-free state to a diffusive state. Rather, for stress boundary conditions, both of the regimes remain diffusive for the data range that we explored.
$Ra^{3/2}$
scaling is often interpreted as indicative of a diffusion-free regime, our analysis reveals that other dynamics remain influenced by diffusive processes. This is evidenced by a Reynolds number scaling (see discussion below) that deviates from the diffusion-free expectation. Hence the observed transition does not signify a complete shift from a truly diffusion-free state to a diffusive state. Rather, for stress boundary conditions, both of the regimes remain diffusive for the data range that we explored.
To assess whether the diffusion-free regime has been achieved conclusively for stress-free cases, we analyse the scaling of
![]() $Re$
as a function of
$Re$
as a function of
![]() $Ra$
across various
$Ra$
across various
![]() $Ek$
. Figure 4(c) depicts
$Ek$
. Figure 4(c) depicts
![]() $Re$
versus
$Re$
versus
![]() $Ra$
, showing a steep increase in
$Ra$
, showing a steep increase in
![]() $Re$
at lower
$Re$
at lower
![]() $Ra$
within the rotation-dominated regime. In the range of
$Ra$
within the rotation-dominated regime. In the range of
![]() $Ra$
where diffusion-free heat transfer is observed,
$Ra$
where diffusion-free heat transfer is observed,
![]() $Re$
follows the scaling
$Re$
follows the scaling
![]() $Re \sim Ra^{11/8}Ek^{3/2}$
(see figure 4
d), which deviates significantly from the diffusion-free Reynolds scaling
$Re \sim Ra^{11/8}Ek^{3/2}$
(see figure 4
d), which deviates significantly from the diffusion-free Reynolds scaling
![]() $Re \sim Ra\,Ek$
(Aurnou, Horn & Julien Reference Aurnou, Horn and Julien2020; Song et al. Reference Song, Shishkina and Zhu2024c
). Consequently, even though the heat transfer scaling exponent reaches
$Re \sim Ra\,Ek$
(Aurnou, Horn & Julien Reference Aurnou, Horn and Julien2020; Song et al. Reference Song, Shishkina and Zhu2024c
). Consequently, even though the heat transfer scaling exponent reaches
![]() $3/2$
, the Reynolds number does not adhere to the expected linear
$3/2$
, the Reynolds number does not adhere to the expected linear
![]() $Ra$
dependence. This indicates that the true diffusion-free regime has not yet been realized in the stress-free DNS. In the next section, we will demonstrate that this observed scaling can be derived from the transitional scaling
$Ra$
dependence. This indicates that the true diffusion-free regime has not yet been realized in the stress-free DNS. In the next section, we will demonstrate that this observed scaling can be derived from the transitional scaling
![]() $Ra_T$
. As
$Ra_T$
. As
![]() $Ra$
increases further,the
$Ra$
increases further,the
![]() $Re$
scaling (again similar to the no-slip counterpart), just like
$Re$
scaling (again similar to the no-slip counterpart), just like
![]() $Nu$
, gradually approaches the non-rotating convection relation
$Nu$
, gradually approaches the non-rotating convection relation
![]() $Re \sim Ra^{1/2}$
(Ahlers et al. Reference Ahlers, Grossmann and Lohse2009; Lohse & Shishkina Reference Lohse and Shishkina2024), marking the transition to buoyancy-dominated dynamics. This shift reflects a regime where buoyancy forces dominate rotational influences, fundamentally altering the flow behaviour.
$Re \sim Ra^{1/2}$
(Ahlers et al. Reference Ahlers, Grossmann and Lohse2009; Lohse & Shishkina Reference Lohse and Shishkina2024), marking the transition to buoyancy-dominated dynamics. This shift reflects a regime where buoyancy forces dominate rotational influences, fundamentally altering the flow behaviour.
4. Transition with stress-free boundary condition
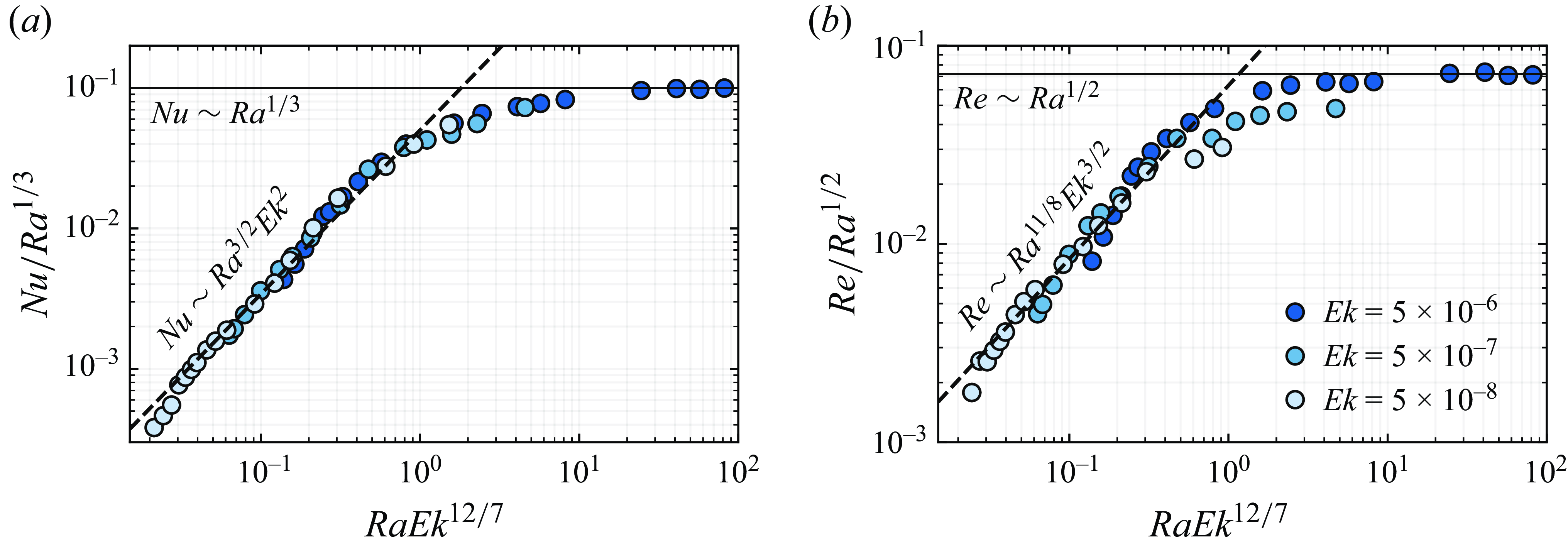
Figure 5. Transition in stress-free RRB convection: (a) Nusselt number (
![]() $Nu$
) normalized by
$Nu$
) normalized by
![]() $Ra^{1/3}$
, and (b) Reynolds number (
$Ra^{1/3}$
, and (b) Reynolds number (
![]() $Re$
) normalized by
$Re$
) normalized by
![]() $Ra^{1/2}$
, are shown as functions of
$Ra^{1/2}$
, are shown as functions of
![]() $Ra$
, normalized by the transitional Rayleigh number
$Ra$
, normalized by the transitional Rayleigh number
![]() $Ra_T \sim Ek^{-12/7}$
for different
$Ra_T \sim Ek^{-12/7}$
for different
![]() $Ek$
at fixed
$Ek$
at fixed
![]() $Pr=1$
.
$Pr=1$
.
As discussed in § 1, the transition between the rotation- and buoyancy-dominated regimes in RRB convection can be determined by equating the
![]() $Nu$
scaling laws for the two regimes. For the no-slip boundary condition,
$Nu$
scaling laws for the two regimes. For the no-slip boundary condition,
![]() $Ra_T \sim Ek^{-3/2}$
is obtained by equating
$Ra_T \sim Ek^{-3/2}$
is obtained by equating
![]() $Nu \sim Ra^3 Ek^4$
, a typical scaling for the rotation-dominated regime, with
$Nu \sim Ra^3 Ek^4$
, a typical scaling for the rotation-dominated regime, with
![]() $Nu \sim Ra^{1/3}$
, the classical scaling for the buoyancy-dominated regime. It is important to note that if
$Nu \sim Ra^{1/3}$
, the classical scaling for the buoyancy-dominated regime. It is important to note that if
![]() $Ra_T$
exists, then the scaling relations for both
$Ra_T$
exists, then the scaling relations for both
![]() $Nu$
and
$Nu$
and
![]() $Re$
should yield consistent results. From Song et al. (Reference Song, Shishkina and Zhu2024c
), it is known that when
$Re$
should yield consistent results. From Song et al. (Reference Song, Shishkina and Zhu2024c
), it is known that when
![]() $Nu \sim Ra^3 Ek^4$
, the Reynolds number follows
$Nu \sim Ra^3 Ek^4$
, the Reynolds number follows
![]() $Re \sim Ra^{5/2}Ek^3$
. In the classical regime of non-rotating Rayleigh–Bénard convection,
$Re \sim Ra^{5/2}Ek^3$
. In the classical regime of non-rotating Rayleigh–Bénard convection,
![]() $Re$
scales close to
$Re$
scales close to
![]() $Re \sim Ra^{1/2}$
. Equating these two
$Re \sim Ra^{1/2}$
. Equating these two
![]() $Re$
scalings also leads to
$Re$
scalings also leads to
![]() $Ra_T \sim Ek^{-3/2}$
, reinforcing the consistency of the scaling arguments derived from both heat and momentum transport.
$Ra_T \sim Ek^{-3/2}$
, reinforcing the consistency of the scaling arguments derived from both heat and momentum transport.
Now we come to the stress-free boundary condition cases. In the rotation-dominated regime for stress-free RRBconvection, the typical scaling is
![]() $Nu \sim Ra^{3/2}Ek^2$
, while in the buoyancy-dominated regime, the scaling is again the classical
$Nu \sim Ra^{3/2}Ek^2$
, while in the buoyancy-dominated regime, the scaling is again the classical
![]() $Nu \sim Ra^{1/3}$
. By equating these two scalings, the transitional
$Nu \sim Ra^{1/3}$
. By equating these two scalings, the transitional
![]() $Ra$
is derived as
$Ra$
is derived as
![]() $Ra_T \sim Ek^{-12/7}$
for stress-free boundary conditions. This prediction for
$Ra_T \sim Ek^{-12/7}$
for stress-free boundary conditions. This prediction for
![]() $Ra_T$
is verified using DNS data for the stress-free case, as shown in figures 5(a) and 5(b) for both
$Ra_T$
is verified using DNS data for the stress-free case, as shown in figures 5(a) and 5(b) for both
![]() $Nu$
and
$Nu$
and
![]() $Re$
. While the transition
$Re$
. While the transition
![]() $Ra_T \approx \mathcal{O}(10)\,Ek^{-12/7}$
is clearly observed at
$Ra_T \approx \mathcal{O}(10)\,Ek^{-12/7}$
is clearly observed at
![]() $Ek = 5 \times 10^{-6}$
, for
$Ek = 5 \times 10^{-6}$
, for
![]() $Ek = 5 \times 10^{-7}$
and
$Ek = 5 \times 10^{-7}$
and
![]() $Ek = 5 \times 10^{-8}$
, the available data suggest a similar trend, although the range of
$Ek = 5 \times 10^{-8}$
, the available data suggest a similar trend, although the range of
![]() $Ra$
explored is more restricted due to computational constraints, and will be verified in the future.
$Ra$
explored is more restricted due to computational constraints, and will be verified in the future.
It is observed that beyond
![]() $Ra_T$
, both
$Ra_T$
, both
![]() $Nu$
and
$Nu$
and
![]() $Re$
approach their non-rotating values, indicating that the flow has transitioned into the buoyancy-dominated regime. Additionally, using the scaling
$Re$
approach their non-rotating values, indicating that the flow has transitioned into the buoyancy-dominated regime. Additionally, using the scaling
![]() $Ra_T \sim Ek^{-12/7}$
, the
$Ra_T \sim Ek^{-12/7}$
, the
![]() $Re$
value in the rotation-dominated regime for stress-free RRB convection can also be derived as
$Re$
value in the rotation-dominated regime for stress-free RRB convection can also be derived as
![]() $Re \sim Ra^{11/8}Ek^{3/2}$
(see figure 4
c,d) by equating the scaling for the buoyancy-dominated region, where
$Re \sim Ra^{11/8}Ek^{3/2}$
(see figure 4
c,d) by equating the scaling for the buoyancy-dominated region, where
![]() $Re \sim Ra^{1/2}$
, with the scaling of
$Re \sim Ra^{1/2}$
, with the scaling of
![]() $Ra_T$
.
$Ra_T$
.
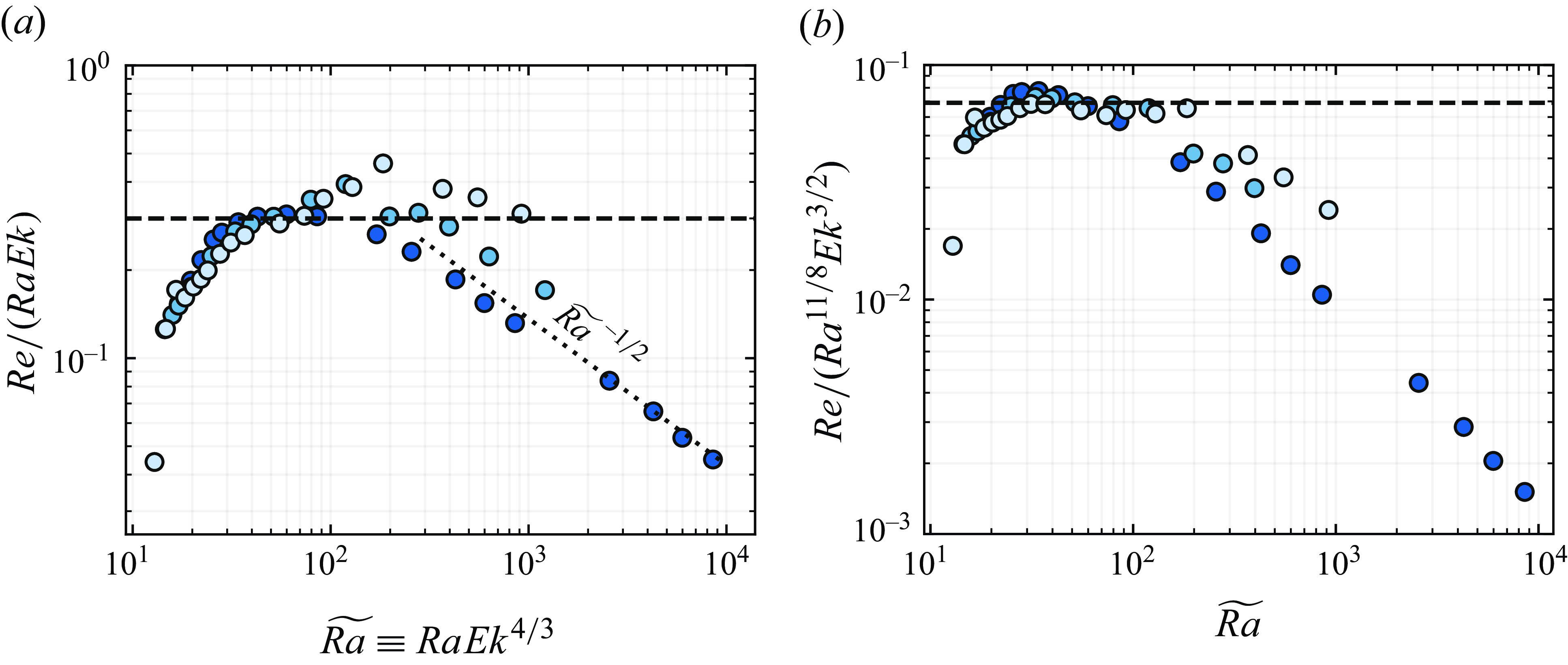
Figure 6. Dimensionless momentum transport
![]() $Re$
, normalized by (a) diffusion-free
$Re$
, normalized by (a) diffusion-free
![]() $Ra\,Ek$
scaling and (b)
$Ra\,Ek$
scaling and (b)
![]() $Ra^{11/8}Ek^{3/2}$
scaling proposed in this work, shown as a function of supercriticality
$Ra^{11/8}Ek^{3/2}$
scaling proposed in this work, shown as a function of supercriticality
![]() $\widetilde {Ra} = Ra\, Ek^{4/3}$
.
$\widetilde {Ra} = Ra\, Ek^{4/3}$
.
In stress-free rotating convection, the classical diffusion-free scaling
![]() $Re \sim Ra\, Ek$
is expected when inertial effects are negligible. However, our analysis reveals that the formation of large-scale vortices leads to enhanced momentum transport, resulting in a scaling
$Re \sim Ra\, Ek$
is expected when inertial effects are negligible. However, our analysis reveals that the formation of large-scale vortices leads to enhanced momentum transport, resulting in a scaling
![]() $Re \sim Ra^{11/8} \: Ek^{3/2}$
. Figure 6 again illustrates that at moderate
$Re \sim Ra^{11/8} \: Ek^{3/2}$
. Figure 6 again illustrates that at moderate
![]() $Ra$
, the measured Reynolds number follows the steeper
$Ra$
, the measured Reynolds number follows the steeper
![]() $Ra^{11/8}\: Ek^{3/2}$
trend, consistent with the impact of the inverse energy cascade associated with large-scale vortices formation.
$Ra^{11/8}\: Ek^{3/2}$
trend, consistent with the impact of the inverse energy cascade associated with large-scale vortices formation.
Recent numerical simulations by Oliver et al. (Reference Oliver, Jacobi, Julien and Calkins2023), employing an asymptotically reduced model, suggest a scaling
![]() $Re \sim Ra^{1.325}$
based on an empirical fit to their data within the range
$Re \sim Ra^{1.325}$
based on an empirical fit to their data within the range
![]() $40 \leqslant \widetilde {Ra} \leqslant 200$
. This exponent is close to the
$40 \leqslant \widetilde {Ra} \leqslant 200$
. This exponent is close to the
![]() $11/8 = 1.375$
scaling obtained in the present work for moderately supercritical parameters.
$11/8 = 1.375$
scaling obtained in the present work for moderately supercritical parameters.
Additionally, for a fixed rotation rate (fixed
![]() $Ek$
) but increasing
$Ek$
) but increasing
![]() $Ra$
, the transport properties tend towards those in the non-rotating case, i.e.
$Ra$
, the transport properties tend towards those in the non-rotating case, i.e.
![]() $Re \sim Ra^{1/2}$
, denoting the transition from a rotation-dominatedregime to a buoyancy-dominated regime. This behaviour is fully captured by the scaling
$Re \sim Ra^{1/2}$
, denoting the transition from a rotation-dominatedregime to a buoyancy-dominated regime. This behaviour is fully captured by the scaling
![]() $Re/ (Ra\, Ek ) \sim Ra^{-1/2}$
, shown as a dotted line in figure 6(a).
$Re/ (Ra\, Ek ) \sim Ra^{-1/2}$
, shown as a dotted line in figure 6(a).
Having examined the transition based on the scaling laws of
![]() $Nu$
at different regimes in the RRB convection framework, it is also worthwhile to consider the transition based on the convective Rossby number
$Nu$
at different regimes in the RRB convection framework, it is also worthwhile to consider the transition based on the convective Rossby number
![]() $Ro$
, which is defined as the ratio of thermal buoyancy to the Coriolis force. It has been argued that the convection regime dominated by rotation extends from the onset of rotating convection up to where
$Ro$
, which is defined as the ratio of thermal buoyancy to the Coriolis force. It has been argued that the convection regime dominated by rotation extends from the onset of rotating convection up to where
![]() $Ro \lesssim 1$
(Zhong & Ahlers Reference Zhong and Ahlers2010; Stevens, Clercx & Lohse Reference Stevens, Clercx and Lohse2013). However, it has been shown that the
$Ro \lesssim 1$
(Zhong & Ahlers Reference Zhong and Ahlers2010; Stevens, Clercx & Lohse Reference Stevens, Clercx and Lohse2013). However, it has been shown that the
![]() $Ro$
normalization does not accurately define the transition. Our results, as shown in figure 7(a) for the stress-free RRB convection cases, are consistent with previous observations (King et al. Reference King, Stellmach, Noir, Hansen and Aurnou2009; Cheng et al. Reference Cheng, Stellmach, Ribeiro, Grannan, King and Aurnou2015). These observations suggest that distinctly smaller scale motions contribute to convective heat transfer, and the system scale parameter
$Ro$
normalization does not accurately define the transition. Our results, as shown in figure 7(a) for the stress-free RRB convection cases, are consistent with previous observations (King et al. Reference King, Stellmach, Noir, Hansen and Aurnou2009; Cheng et al. Reference Cheng, Stellmach, Ribeiro, Grannan, King and Aurnou2015). These observations suggest that distinctly smaller scale motions contribute to convective heat transfer, and the system scale parameter
![]() $Ro$
does not collapse the data well.
$Ro$
does not collapse the data well.
Alternatively, local Rossby numbers are defined in the literature to predict the transition. This is given by the expression (Christensen & Aubert Reference Christensen and Aubert2006; Sreenivasan & Jones Reference Sreenivasan and Jones2006)
This formulation was used by Cheng et al. (Reference Cheng, Stellmach, Ribeiro, Grannan, King and Aurnou2015) to test whether
![]() $Ro_\ell$
can predict the rotation-dominant and buoyancy-dominant transitions in RRB convection simulations. However, in their experiments, they were unable to measure velocities directly, so they rewrote the equation as
$Ro_\ell$
can predict the rotation-dominant and buoyancy-dominant transitions in RRB convection simulations. However, in their experiments, they were unable to measure velocities directly, so they rewrote the equation as
![]() $Ro_\ell = \sqrt { ({Ra}/{Pr}}) \, Ek \, ({L}/{\ell })$
, substituting
$Ro_\ell = \sqrt { ({Ra}/{Pr}}) \, Ek \, ({L}/{\ell })$
, substituting
![]() $\ell \sim Ek^{1/3}$
and assuming
$\ell \sim Ek^{1/3}$
and assuming
![]() $Re \sim (Nu - 1)^{1/2} Ra^{1/2} Ek^{1/3}/Pr$
. This formulation allowed them to collapse the data well for
$Re \sim (Nu - 1)^{1/2} Ra^{1/2} Ek^{1/3}/Pr$
. This formulation allowed them to collapse the data well for
![]() $Pr \approx 7$
.
$Pr \approx 7$
.
In contrast, our work is based on DNS, so we directly computed the time-averaged dominant length scale from the vertical velocity spectra, and substituted it into the
![]() $Ro_\ell$
formulation. As shown in figure 7(b), we find that this formulation predicts the transition more accurately compared to
$Ro_\ell$
formulation. As shown in figure 7(b), we find that this formulation predicts the transition more accurately compared to
![]() $Ro$
, even for the
$Ro$
, even for the
![]() $Pr = 1$
simulations performed in this study. For
$Pr = 1$
simulations performed in this study. For
![]() $Ro_\ell \gt 1$
, the flow approaches the buoyancy-dominated regime. It is important to note that the depth-averaged flow is subtracted from the total flow when computing the length scale, particularly for cases exhibiting large-scale vortices.
$Ro_\ell \gt 1$
, the flow approaches the buoyancy-dominated regime. It is important to note that the depth-averaged flow is subtracted from the total flow when computing the length scale, particularly for cases exhibiting large-scale vortices.
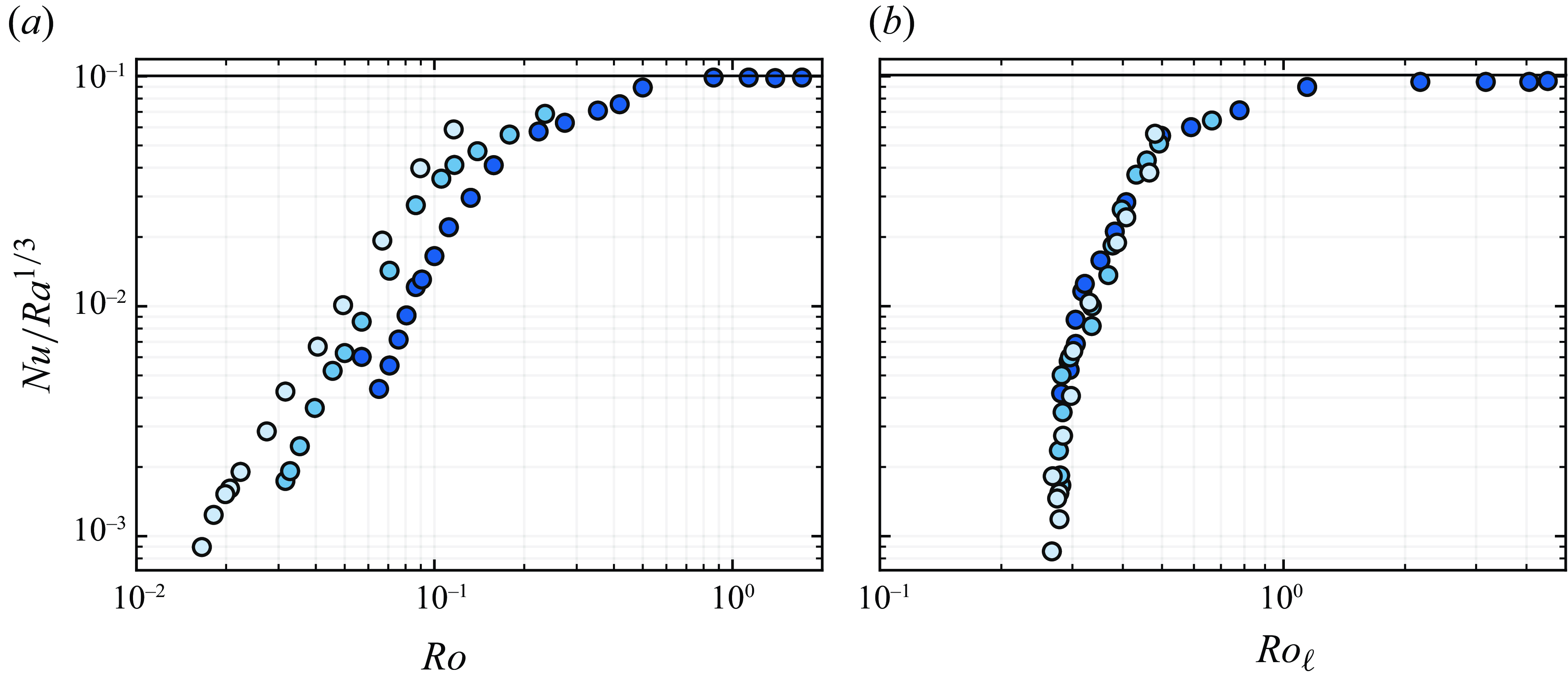
Figure 7. Transition in stress-free RRB convection based on Rossby number, with
![]() $Nu$
normalized by
$Nu$
normalized by
![]() $Ra^{1/3}$
shown as a function of (a) convective Rossby number
$Ra^{1/3}$
shown as a function of (a) convective Rossby number
![]() $Ro$
and (b) local Rossby number
$Ro$
and (b) local Rossby number
![]() $Ro_\ell = Ro \times L/\ell$
based on convective length scale
$Ro_\ell = Ro \times L/\ell$
based on convective length scale
![]() $\ell /L$
.
$\ell /L$
.
5. Transition in the homogeneous rotating condition
Homogeneous rotating convection refers to a simplified configuration of RRB convection in which the effects of solid boundaries are removed. The flow occurs in an unbounded, periodic domain and is driven by an imposed linear temperature gradient in the vertical direction, which is parallel to both the rotational and gravitational axes. This paradigm is also frequently employed to investigate the ultimate turbulent state predicted by Kraichnan (Reference Kraichnan1962). Such a state is theorized to arise in Rayleigh–Bénard convection when the boundary layer contribution to heat transfer becomes negligible (Grossmann & Lohse Reference Grossmann and Lohse2004). Numerical experiments have demonstrated that this set-up exhibits the ultimate regime both with and without rotation (Lohse & Toschi Reference Lohse and Toschi2003; Calzavarini et al. Reference Calzavarini, Lohse, Toschi and Tripiccione2005; Toselli et al. Reference Toselli, Musacchio and Boffetta2019). By eliminating Ekman boundary layers, this configuration serves as a valuable model for studying geophysical and astrophysical flows, where boundary effects are minimal.
Additionally, while both homogeneous convection and stress-free convection eliminate Ekman boundary layers, they differ in domain geometry. In homogeneous convection, the absence of physical boundaries – with periodic boundary conditions applied in all directions – removes not only Ekman layers but also any wall-induced constraints, resulting in distinct flow dynamics. In contrast, stress-free convection remains confined between two plates, which impose discrete vertical modes and influence the thermal boundary layers. These geometric differences can lead to distinct transitional scaling behaviours, with stress-free convection exhibiting different scaling properties compared to homogeneous convection.
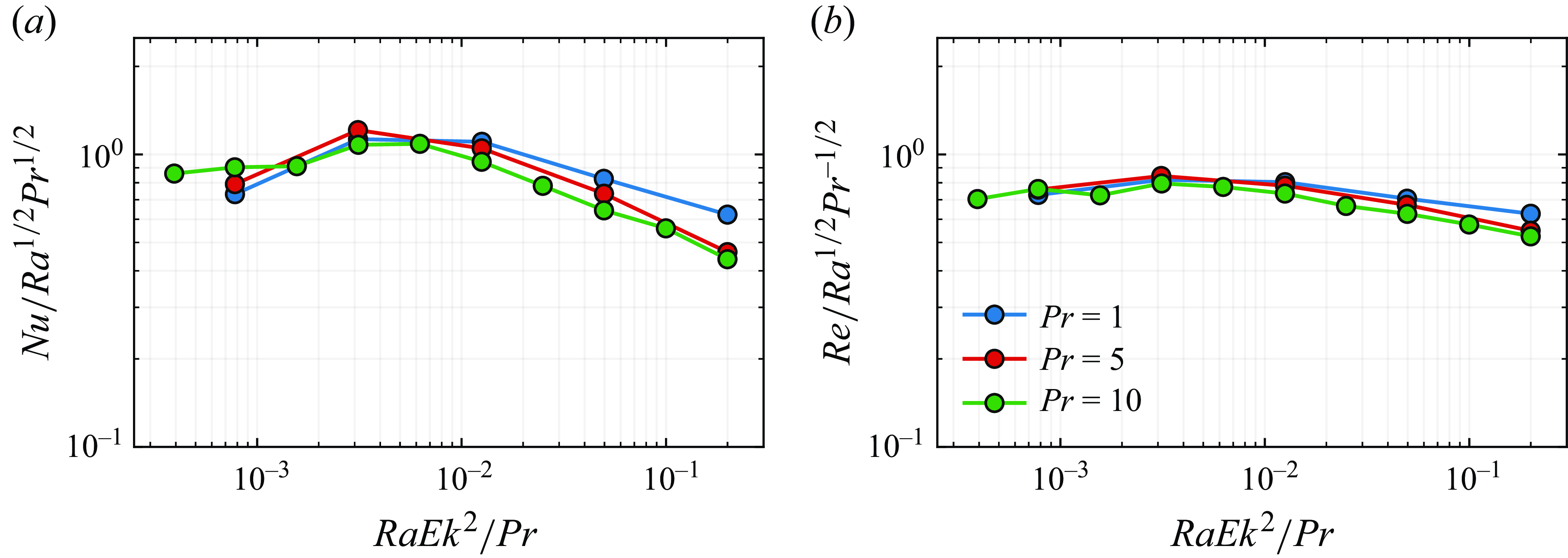
Figure 8. Transition in homogeneous RRB convection: (a)
![]() $Nu$
normalized by
$Nu$
normalized by
![]() $Ra^{1/2}Pr^{1/2}$
, and (b)
$Ra^{1/2}Pr^{1/2}$
, and (b)
![]() $Re$
normalized by
$Re$
normalized by
![]() $Ra^{1/2}Pr^{-1/2}$
, shown as functions of
$Ra^{1/2}Pr^{-1/2}$
, shown as functions of
![]() $Ra$
, normalized by
$Ra$
, normalized by
![]() $Ra_T \sim Ek^{-2}Pr$
for different
$Ra_T \sim Ek^{-2}Pr$
for different
![]() $Pr$
. Data are taken from DNS by Toselli et al. (Reference Toselli, Musacchio and Boffetta2019).
$Pr$
. Data are taken from DNS by Toselli et al. (Reference Toselli, Musacchio and Boffetta2019).
Notably, in homogeneous rotating convection, both the rotation-dominated and buoyancy-dominated regimes correspond to the diffusion-free ultimate regime. This dual correspondence underscores the asymptotic nature of transport dynamics in such flows.
In the rotation-dominated regime,
![]() $Nu$
scales as
$Nu$
scales as
![]() $Nu \sim Ra^{3/2}Ek^2Pr^{-1/2}$
(Aurnou et al. Reference Aurnou, Horn and Julien2020; Song et al. Reference Song, Shishkina and Zhu2024c
), reflecting the diffusion-free regime scaling. In contrast, the buoyancy-dominated regime follows the scaling
$Nu \sim Ra^{3/2}Ek^2Pr^{-1/2}$
(Aurnou et al. Reference Aurnou, Horn and Julien2020; Song et al. Reference Song, Shishkina and Zhu2024c
), reflecting the diffusion-free regime scaling. In contrast, the buoyancy-dominated regime follows the scaling
![]() $Nu \sim Ra^{1/2}Pr^{1/2}$
(Lohse & Toschi Reference Lohse and Toschi2003; Toselli et al. Reference Toselli, Musacchio and Boffetta2019), where buoyancy forces dominate, and the transport characteristics align with the ultimate regime for non-rotating convection. By equating these two diffusion-free scaling laws for
$Nu \sim Ra^{1/2}Pr^{1/2}$
(Lohse & Toschi Reference Lohse and Toschi2003; Toselli et al. Reference Toselli, Musacchio and Boffetta2019), where buoyancy forces dominate, and the transport characteristics align with the ultimate regime for non-rotating convection. By equating these two diffusion-free scaling laws for
![]() $Nu$
,
$Nu$
,
![]() $Ra_T$
is derived as
$Ra_T$
is derived as
![]() $Ra_T \sim Ek^{-2}Pr$
. Similarly,
$Ra_T \sim Ek^{-2}Pr$
. Similarly,
![]() $Re$
exhibits scaling behaviour consistent with the diffusion-free regime. In the rotation-dominated regime,
$Re$
exhibits scaling behaviour consistent with the diffusion-free regime. In the rotation-dominated regime,
![]() $Re \sim Ra\,Ek\,Pr^{-1}$
(Aurnou et al. Reference Aurnou, Horn and Julien2020; Song et al. Reference Song, Shishkina and Zhu2024c
). In the buoyancy-dominated regime,
$Re \sim Ra\,Ek\,Pr^{-1}$
(Aurnou et al. Reference Aurnou, Horn and Julien2020; Song et al. Reference Song, Shishkina and Zhu2024c
). In the buoyancy-dominated regime,
![]() $Re \sim Ra^{1/2}Pr^{-1/2}$
(Toselli et al. Reference Toselli, Musacchio and Boffetta2019; Lohse & Shishkina Reference Lohse and Shishkina2024), again reflecting the asymptotic scaling of turbulent convection without rotational constraints. Equating these two scalings for
$Re \sim Ra^{1/2}Pr^{-1/2}$
(Toselli et al. Reference Toselli, Musacchio and Boffetta2019; Lohse & Shishkina Reference Lohse and Shishkina2024), again reflecting the asymptotic scaling of turbulent convection without rotational constraints. Equating these two scalings for
![]() $Re$
leads to the same relation, i.e.
$Re$
leads to the same relation, i.e.
![]() $Ra_T \sim Ek^{-2}Pr$
. The consistency of
$Ra_T \sim Ek^{-2}Pr$
. The consistency of
![]() $Ra_T$
obtained from both
$Ra_T$
obtained from both
![]() $Nu$
and
$Nu$
and
![]() $Re$
confirms the robustness of this approach and underscores the diffusion-free nature of transport in both regimes.
$Re$
confirms the robustness of this approach and underscores the diffusion-free nature of transport in both regimes.
The scaling for
![]() $Ra_T$
is validated using DNS data from Toselli et al. (Reference Toselli, Musacchio and Boffetta2019) for homogeneous convection at
$Ra_T$
is validated using DNS data from Toselli et al. (Reference Toselli, Musacchio and Boffetta2019) for homogeneous convection at
![]() $Ra = 1.1 \times 10^7$
and
$Ra = 1.1 \times 10^7$
and
![]() $2.2 \times 10^7$
,
$2.2 \times 10^7$
,
![]() $Pr \in \{1, 5, 10\}$
and
$Pr \in \{1, 5, 10\}$
and
![]() $Ek \in [3 \times 10^{-4}, 6 \times 10^{-6}]$
. Figure 8(a,b) present
$Ek \in [3 \times 10^{-4}, 6 \times 10^{-6}]$
. Figure 8(a,b) present
![]() $Nu$
and
$Nu$
and
![]() $Re$
from the DNS data plotted against the predicted
$Re$
from the DNS data plotted against the predicted
![]() $Ra_T$
scaling. For the available dataset, the
$Ra_T$
scaling. For the available dataset, the
![]() $Ra_T$
scaling demonstrates good data collapse, suggesting that the overall dynamics is well captured by the predicted scaling. This indicates that
$Ra_T$
scaling demonstrates good data collapse, suggesting that the overall dynamics is well captured by the predicted scaling. This indicates that
![]() $Ra_T$
for the homogeneous case can be estimated reliably using the proposed theory.
$Ra_T$
for the homogeneous case can be estimated reliably using the proposed theory.
It is worth noting that the primary focus of Toselli et al. (Reference Toselli, Musacchio and Boffetta2019) was to examine heat transfer enhancement in the weakly rotating regime. Consequently, the steep scaling regime – expected to appear on the left-hand side of the figure (
![]() $Ra\,Ek^2/Pr\lt 10^{-4}$
)–is not represented in the data. Although the current dataset does not include additional points in the transition region due to inherent limitations in the simulation parameter range, the observed trend remains consistent with the expected transition behaviour. We acknowledge that the present data may not fully capture the detailed dynamics of the transition, and future investigations with an extended parameter space are planned to further elucidate these dynamics.
$Ra\,Ek^2/Pr\lt 10^{-4}$
)–is not represented in the data. Although the current dataset does not include additional points in the transition region due to inherent limitations in the simulation parameter range, the observed trend remains consistent with the expected transition behaviour. We acknowledge that the present data may not fully capture the detailed dynamics of the transition, and future investigations with an extended parameter space are planned to further elucidate these dynamics.
This approach – equating the transport parameter scalings (both
![]() $Nu$
and
$Nu$
and
![]() $Re$
) in the rotation-dominated and buoyancy-dominated regimes–proves robust for predicting the transitional Rayleigh number across different boundary condition set-ups within the RRB convection framework. The different scalings for no-slip, stress-free and homogeneous RRB convection are summarized in table 1. These scalings reflect the transition between rotation-dominated and buoyancy-dominated regimes. It is important to note that for the no-slip and stress-free boundary conditions, the scaling relations presented in table 1 do not include a dependence on the Prandtl number, as the simulations were conducted and the scalings were verified at a fixed
$Re$
) in the rotation-dominated and buoyancy-dominated regimes–proves robust for predicting the transitional Rayleigh number across different boundary condition set-ups within the RRB convection framework. The different scalings for no-slip, stress-free and homogeneous RRB convection are summarized in table 1. These scalings reflect the transition between rotation-dominated and buoyancy-dominated regimes. It is important to note that for the no-slip and stress-free boundary conditions, the scaling relations presented in table 1 do not include a dependence on the Prandtl number, as the simulations were conducted and the scalings were verified at a fixed
![]() $Pr = 1$
. In contrast, for the homogeneous case, the scaling relations explicitly incorporate the Prandtl number, reflecting both theoretical considerations and the variation in
$Pr = 1$
. In contrast, for the homogeneous case, the scaling relations explicitly incorporate the Prandtl number, reflecting both theoretical considerations and the variation in
![]() $Pr$
across the dataset used in Toselli et al. (Reference Toselli, Musacchio and Boffetta2019).
$Pr$
across the dataset used in Toselli et al. (Reference Toselli, Musacchio and Boffetta2019).
Table 1. Scaling for
![]() $Nu$
and
$Nu$
and
![]() $Re$
in the rotation- and buoyancy-dominated regimes for different boundary conditions in RRB convection, as well as for homogeneous convection, along with the scaling of
$Re$
in the rotation- and buoyancy-dominated regimes for different boundary conditions in RRB convection, as well as for homogeneous convection, along with the scaling of
![]() $Ra_T$
, calculated from both
$Ra_T$
, calculated from both
![]() $Nu$
and
$Nu$
and
![]() $Re$
. Note that for the no-slip and stress-free boundary conditions, the scaling relations do not include Prandtl number dependence, as simulations were conducted at a fixed
$Re$
. Note that for the no-slip and stress-free boundary conditions, the scaling relations do not include Prandtl number dependence, as simulations were conducted at a fixed
![]() $Pr = 1$
. For the homogeneous case,
$Pr = 1$
. For the homogeneous case,
![]() $Pr$
dependence is included explicitly, reflecting theoretical scalings and the dataset’s
$Pr$
dependence is included explicitly, reflecting theoretical scalings and the dataset’s
![]() $Pr$
variation.
$Pr$
variation.

It is also important to emphasize that the homogeneous convection model adopted in this study is an idealized framework designed to isolate the intrinsic, diffusion-free turbulent transport mechanisms in rotating convection. Although geophysical and astrophysical convective layers are indeed bounded – such as Earth’s liquid outer core, which is confined between the solid inner core and the overlying mantle – the effective boundary conditions in these systems can, in some cases, approximate stress-free or even partially free-slip conditions rather than the strict no-slip condition often assumed in laboratory experiments. In this regard, homogeneous convection serves as a useful reference model that strips away the complexities introduced by boundary layers, allowing us to test and validate the diffusion-free scaling laws in the interior flow. We stress that this approach is intended to complement, not replace, more realistic bounded models. In practice, the insights gained from homogeneous convection help to clarify how boundary effects modify the transition between rotation- and buoyancy-dominated regimes in fully bounded systems.
6. Concluding remarks
This study investigated the transition between rotation- and buoyancy-dominated regimes in RRB convection under stress-free and homogeneous boundary conditions. Using DNS and theoretical analysis, we established the scaling for the transitional Rayleigh number
![]() $Ra_T$
, which characterizes the transition from the rotation-dominated regime tothe buoyancy-dominated regime, as a function of control parameters in RRB convection. The scaling for
$Ra_T$
, which characterizes the transition from the rotation-dominated regime tothe buoyancy-dominated regime, as a function of control parameters in RRB convection. The scaling for
![]() $Ra_T$
was derived by equating the scaling laws for Nusselt and Reynolds numbers, in both the rotation-dominated and buoyancy-dominated regimes. The scaling was consistent regardless of whether heat or momentum transport was analysed, with
$Ra_T$
was derived by equating the scaling laws for Nusselt and Reynolds numbers, in both the rotation-dominated and buoyancy-dominated regimes. The scaling was consistent regardless of whether heat or momentum transport was analysed, with
![]() $Ra_T \sim Ek^{-12/7}$
for stress-free boundary conditions, and
$Ra_T \sim Ek^{-12/7}$
for stress-free boundary conditions, and
![]() $Ra_T \sim Ek^{-2} Pr$
for homogeneous conditions. These findings extend the established scaling frameworks developed for no-slip boundary conditions and offer new insights into the effects of boundary conditions on convective transitions.
$Ra_T \sim Ek^{-2} Pr$
for homogeneous conditions. These findings extend the established scaling frameworks developed for no-slip boundary conditions and offer new insights into the effects of boundary conditions on convective transitions.
In the asymptotic limit, the reduced Rayleigh number
![]() $Ra\, Ek^{4/3}$
is assumed to be of order 1, which implies
$Ra\, Ek^{4/3}$
is assumed to be of order 1, which implies
![]() $Ra_T\, Ek^{4/3} \sim Ek^{-1/3}$
(Julien et al. Reference Julien, Knobloch, Rubio and Vasil2012b
; Maffei et al. Reference Maffei, Krouss, Julien and Calkins2021), hence
$Ra_T\, Ek^{4/3} \sim Ek^{-1/3}$
(Julien et al. Reference Julien, Knobloch, Rubio and Vasil2012b
; Maffei et al. Reference Maffei, Krouss, Julien and Calkins2021), hence
![]() $Ra_T \sim Ek^{-5/3}$
. Our DNS results for stress-free boundary conditions indicate that the transitional Rayleigh number scales as
$Ra_T \sim Ek^{-5/3}$
. Our DNS results for stress-free boundary conditions indicate that the transitional Rayleigh number scales as
![]() $Ra_T \sim Ek^{-12/7}$
, with exponent approximately
$Ra_T \sim Ek^{-12/7}$
, with exponent approximately
![]() $-1.71$
. This is in close agreement with the asymptotic prediction
$-1.71$
. This is in close agreement with the asymptotic prediction
![]() $-5/3 \approx -1.67$
, and the small difference can likely be attributed to finite-amplitude effects and higher-order corrections. For homogeneous (triply periodic) convection, the scaling
$-5/3 \approx -1.67$
, and the small difference can likely be attributed to finite-amplitude effects and higher-order corrections. For homogeneous (triply periodic) convection, the scaling
![]() $Ra_T \sim Ek^{-2}$
reflects the distinct flow dynamics that arises in the absence of physical boundaries.
$Ra_T \sim Ek^{-2}$
reflects the distinct flow dynamics that arises in the absence of physical boundaries.
The present work lays the groundwork for exploring extreme regimes relevant to planetary and stellar environments, where stress-free or homogeneous (boundary-free) conditions are more representative. Future research could build upon this foundation by investigating a wider range of Prandtl numbers and rotation rates, further broadening the applicability of these insights to the complex dynamics of rotating fluids.
Acknowledgements.
We gratefully acknowledge the financial support from the Max Planck Society and the German Research Foundation through grants 521319293, 540422505 and 550262949. All the simulations have been conducted on the HPC systems of the Max Planck Computing and Data Facility (MPCDF) as well as the National High Performance Computing (NHR@ZIB and NHR-Nord@Göttingen).
Declaration of interests.
The authors report no conflict of interest.
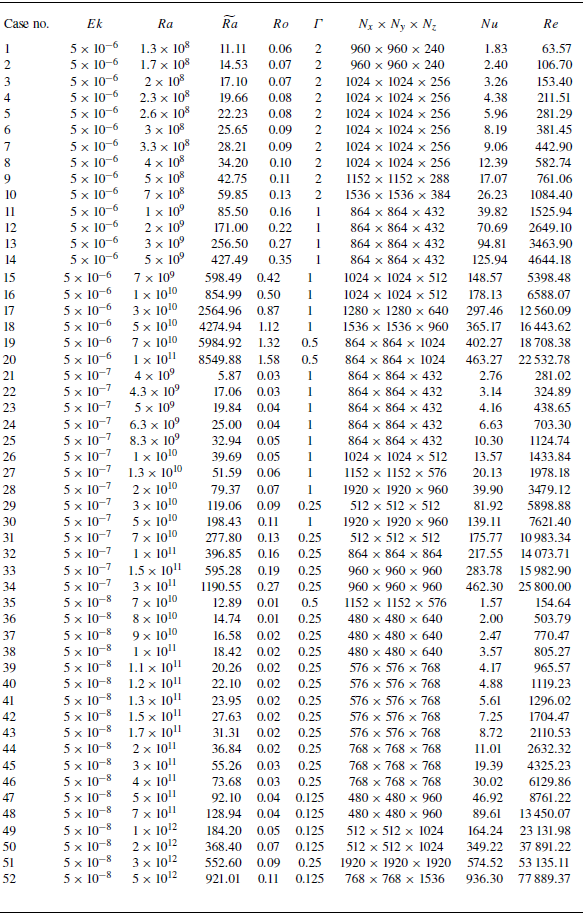
Appendix A. Numerical parameters and grid resolutions
The range of parameters investigated, together with the associated grid resolution and transport parameters, for the current DNS of stress-free RRB convection is outlined in Table 2.
Table 2. (cntd). Summary of the parameters considered in this study:
![]() $Ek$
is the Ekman number,
$Ek$
is the Ekman number,
![]() $Ra$
is the Rayleigh number,
$Ra$
is the Rayleigh number,
![]() $\widetilde {Ra} \equiv Ra\,Ek^{4/3}$
is the reduced Rayleigh number,
$\widetilde {Ra} \equiv Ra\,Ek^{4/3}$
is the reduced Rayleigh number,
![]() $Ro = \sqrt {Ra/Pr}\,Ek$
is the convective Rossby number,
$Ro = \sqrt {Ra/Pr}\,Ek$
is the convective Rossby number,
![]() $\Gamma$
is the ratio of the width to the height of the computational domain,
$\Gamma$
is the ratio of the width to the height of the computational domain,
![]() $Nu$
is the Nusselt number, and
$Nu$
is the Nusselt number, and
![]() $Re$
is the Reynolds number, computed from the root mean square of the vertical component of velocity. The Prandtl number
$Re$
is the Reynolds number, computed from the root mean square of the vertical component of velocity. The Prandtl number
![]() $Pr$
is fixed at 1 for all simulations.
$Pr$
is fixed at 1 for all simulations.