Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hamed, Ali M.
Castillo, Luciano
and
Chamorro, Leonardo P.
2017.
Turbulent boundary layer response to large-scale wavy topographies.
Physics of Fluids,
Vol. 29,
Issue. 6,
Hamed, A. M.
and
Chamorro, L. P.
2018.
Turbulent boundary layer around 2D permeable and impermeable obstacles.
Experiments in Fluids,
Vol. 59,
Issue. 9,
Martins Segunda, Vinicius
Ormiston, Scott J.
and
Tachie, Mark F.
2018.
Experimental and numerical investigation of developing turbulent flow over a wavy wall in a horizontal channel.
European Journal of Mechanics - B/Fluids,
Vol. 68,
Issue. ,
p.
128.
He, Jiyang
Butler, Adam
and
Wu, Xuesong
2019.
Effects of distributed roughness on crossflow instability through generalized resonance mechanisms.
Journal of Fluid Mechanics,
Vol. 858,
Issue. ,
p.
787.
Hamed, Ali M.
Peterlein, Adam M.
and
Randle, Lindsey V.
2019.
Turbulent boundary layer perturbation by two wall-mounted cylindrical roughness elements arranged in tandem: Effects of spacing and height ratio.
Physics of Fluids,
Vol. 31,
Issue. 6,
Lu, Yuhan
Zeng, Fanzhi
Liu, Hongkang
Liu, Zaijie
and
Yan, Chao
2021.
Direct numerical simulation of roughness-induced transition controlled by two-dimensional wall blowing.
Journal of Fluid Mechanics,
Vol. 920,
Issue. ,
Mateo-Gabín, Andrés
Chávez, Miguel
Garicano-Mena, Jesús
and
Valero, Eusebio
2021.
Wavy Walls, a Passive Way to Control the Transition to Turbulence. Detailed Simulation and Physical Explanation.
Energies,
Vol. 14,
Issue. 13,
p.
3937.
Lu, Yuhan
Liu, Zaijie
Sun, Mao
Zhou, Teng
and
Yan, Chao
2022.
Control of roughness-induced transition under the influence of inflow disturbance.
Acta Astronautica,
Vol. 193,
Issue. ,
p.
110.
Zhang, Enwei
Wu, Wangxia
Liu, Qingquan
and
Wang, Xiaoliang
2022.
Effects of vortex formation and interaction on turbulent mass transfer over a two-dimensional wavy wall.
Physical Review Fluids,
Vol. 7,
Issue. 11,
Liu, Zaijie
Huang, Hexia
Tan, Huijun
and
Liu, Mengying
2024.
Control of roughness-induced transition in supersonic flows by local wall heating strips.
Journal of Fluid Mechanics,
Vol. 999,
Issue. ,
Liu, Zaijie
Lu, Yuhan
Liang, Jianhan
and
Huang, Hexia
2024.
Roughness-Induced Transition in Supersonic Boundary Layers with Wall Heating and Cooling Effects.
AIAA Journal,
Vol. 62,
Issue. 7,
p.
2458.
Zhang, Enwei
Wang, Zhan
and
Liu, Qingquan
2024.
Turbulent momentum and kinetic energy transfer of channel flow over three-dimensional wavy walls.
Physical Review Fluids,
Vol. 9,
Issue. 3,
Huang, Hexia
Liu, Zaijie
Liu, Mengying
and
Tan, Huijun
2024.
Direct numerical simulation of distributed roughness induced transition in a supersonic boundary layer.
Physics of Fluids,
Vol. 36,
Issue. 12,
Jain, Ishita
Katiyar, S.
and
Sarkar, S.
2024.
Influence of riblet geometry and freestream turbulence on boundary layer transition.
Physics of Fluids,
Vol. 36,
Issue. 12,
Yu, Linmeng
Sun, Jiao
Sun, Kangfu
Yuan, Pengda
and
Chen, Wenyi
2025.
Effect of a perforation on the flow characteristics of corrugated wall.
Experimental Thermal and Fluid Science,
Vol. 161,
Issue. ,
p.
111358.
De la Cruz-Ávila, Mauricio
Castillo-Guerrero, Francisco J.
Barrios-Pina, Hector
and
Bonasia, Rosanna
2025.
Numerical three-dimensional forecasting of a river section under abnormal discharge conditions due to a tropical storm: A case study on Santa Catarina River, México.
Results in Engineering,
Vol. 26,
Issue. ,
p.
105067.
Ye, Qingqing
Avallone, Francesco
Ragni, Daniele
and
Casalino, Damiano
2025.
Boundary layer transition induced by roughness arrays over NACA 0012 airfoil.
Experimental Thermal and Fluid Science,
Vol. 168,
Issue. ,
p.
111505.
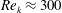 $Re_{k}\approx 300$ . Systematic experiments were performed using high-spatial-resolution planar particle image velocimetry (PIV) in a refractive-index-matching (RIM) channel, where the roughness covered the entire length of the test section. The results show that the flow over the 2D roughness becomes turbulent much sooner than its 3D counterpart (
$Re_{k}\approx 300$ . Systematic experiments were performed using high-spatial-resolution planar particle image velocimetry (PIV) in a refractive-index-matching (RIM) channel, where the roughness covered the entire length of the test section. The results show that the flow over the 2D roughness becomes turbulent much sooner than its 3D counterpart ( 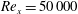 $Re_{x}=50\,000$ versus 120 000). This is attributed to the presence of a velocity inflection point resulting from flow separation within the troughs of the 2D roughness. In the transitional region, unsteady disturbances above the two roughnesses appear upstream of near-roughness disturbances. The above-roughness disturbances are associated with the inflection point in the vertically displaced boundary layer for the 2D case, and with the mean velocity deficit resulting from the interaction of the wakes of upstream elements for the 3D case. The near-roughness fluctuations are associated with the shear layer present behind the crests of both roughnesses. The transitional region is characterized by the interaction between above- and near-roughness disturbances, which merge, leading to a rapid vertical growth of the turbulent fluctuations.
$Re_{x}=50\,000$ versus 120 000). This is attributed to the presence of a velocity inflection point resulting from flow separation within the troughs of the 2D roughness. In the transitional region, unsteady disturbances above the two roughnesses appear upstream of near-roughness disturbances. The above-roughness disturbances are associated with the inflection point in the vertically displaced boundary layer for the 2D case, and with the mean velocity deficit resulting from the interaction of the wakes of upstream elements for the 3D case. The near-roughness fluctuations are associated with the shear layer present behind the crests of both roughnesses. The transitional region is characterized by the interaction between above- and near-roughness disturbances, which merge, leading to a rapid vertical growth of the turbulent fluctuations.

