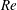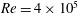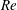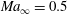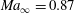1. Introduction
The triple-deck theory was specifically designed with the purpose of describing the phenomenon of boundary-layer separation at large values of the Reynolds number. The basic ideas that underlie the foundation of the triple-deck theory came from experimental studies of boundary-layer separation, including the separation caused by an impinging shock wave, with the then unexplained phenomenon of ‘upstream influence’. These experiments are summarised by Chapman, Kuehn & Larson (Reference Chapman, Kuehn and Larson1958), and early theoretical models to explain the phenomenon are reviewed in a paper by Lighthill (Reference Lighthill2000). As a formal mathematical theory, the triple-deck theory was put forward by Neiland (Reference Neiland1969), Stewartson (Reference Stewartson1969), Stewartson & Williams (Reference Stewartson and Williams1969), Messiter (Reference Messiter1970) and Sychev (Reference Sychev1972), and a detailed description of the basic aspects of the theory can be found in the monograph by Sychev et al. (Reference Sychev, Ruban, Sychev and Korolev1998). According to the triple-deck theory, the flow near the separation point is described by Prandtl’s boundary-layer equations. The main alteration to Prandtl’s classic theory is that the pressure acting on the boundary layer is not known in advance, but has to be found as part of the solution, as it is affected by the displacement effect of the boundary layer. The main advantage of the triple-deck theory is that there are no restrictions on how large the Reynolds number is. In fact, the larger the Reynolds number, the more accurate the theory is. However, numerical solution of the triple-deck equations is rather difficult, especially when the separation region is not small. It took a decade before reliable numerical techniques were developed; see chapter 7 in Sychev et al. (Reference Sychev, Ruban, Sychev and Korolev1998).
Numerical techniques for solving the Navier–Stokes equations have also undergone significant improvement over recent decades. A comprehensive summary of the role of direct numerical simulation (DNS) in fluid mechanics up to 1998 can be found in Moin & Mahesh (Reference Moin and Mahesh1998) and references therein. More recently, compressible DNS has been performed in various works, among which we cite Pirozzoli, Grasso & Gatski (Reference Pirozzoli, Grasso and Gatski2004), Martin (Reference Martin2007), Rizzetta et al. (Reference Rizzetta, Visbal, Reed and Saric2010) and Rizzetta & Visbal (Reference Rizzetta and Visbal2014). Despite all of these advances, the task of calculating large-Reynolds-number separated flows, especially for transonic flow regimes, has been challenging. It is therefore not surprising that there are only a few publications where the Navier–Stokes calculations are compared with the triple-deck predictions; see, for example, Hsiao & Pauley (Reference Hsiao and Pauley1994).
In this paper, we use the subsonic and transonic versions of the triple-deck theory. The governing equations for the subsonic triple-deck theory were formulated by Neiland (Reference Neiland1969), Stewartson (Reference Stewartson1969), Stewartson & Williams (Reference Stewartson and Williams1969), Messiter (Reference Messiter1970) and Sychev (Reference Sychev1972). The transonic version of triple-deck theory was first formulated by Bodonyi & Kluwick (Reference Bodonyi and Kluwick1977), Bodonyi (Reference Bodonyi1979) and Bodonyi & Kluwick (Reference Bodonyi and Kluwick1982, Reference Bodonyi and Kluwick1998). In our calculations we employed the special regime described by Timoshin (Reference Timoshin1990) and Bowles & Smith (Reference Bowles and Smith1993). Concerning the DNS, we solved the two-dimensional compressible Navier–Stokes equations by means of a high-order spectral/
![]() $hp$
element approach, where we used a discontinuous Galerkin (DG) method in space and an explicit fourth-order Runge–Kutta scheme in time. The interested reader can refer to Karniadakis & Sherwin (Reference Karniadakis and Sherwin2005), Hesthaven & Warburton (Reference Hesthaven and Warburton2008) and De Grazia et al. (Reference De Grazia, Mengaldo, Moxey, Vincent and Sherwin2014).
$hp$
element approach, where we used a discontinuous Galerkin (DG) method in space and an explicit fourth-order Runge–Kutta scheme in time. The interested reader can refer to Karniadakis & Sherwin (Reference Karniadakis and Sherwin2005), Hesthaven & Warburton (Reference Hesthaven and Warburton2008) and De Grazia et al. (Reference De Grazia, Mengaldo, Moxey, Vincent and Sherwin2014).
The paper is organised as follows. In § 2 we detail the model problem considered. In § 3 we describe both the triple-deck model employed and the DNS tool used. In § 4 we present the comparison results obtained on the model problem, and in § 5 we briefly summarise the main conclusions of this work.
2. Model problem
The problem considered consists of a two-dimensional flat plate equipped with an isolated roughness element as shown in figure 1. We took into account various roughness heights as well as different free-stream conditions in order to investigate both linear and nonlinear regimes as well as subsonic (case 1) and transonic (case 2) conditions. The shape of the roughness element was given by
where
![]() $L$
is the distance from the centre of the roughness element to the leading edge of the flat plate,
$L$
is the distance from the centre of the roughness element to the leading edge of the flat plate,
![]() $h_{r}$
is the height of the roughness element and
$h_{r}$
is the height of the roughness element and
![]() ${\it\beta}$
is a parameter that controls the shape of the roughness element. In particular,
${\it\beta}$
is a parameter that controls the shape of the roughness element. In particular,
![]() $L$
and
$L$
and
![]() ${\it\beta}$
were fixed and equal to 0.05 m and
${\it\beta}$
were fixed and equal to 0.05 m and
![]() $1.7961\times 10^{-4}~\text{m}$
, respectively. Concerning the height of the roughness element, we took into account three different values:
$1.7961\times 10^{-4}~\text{m}$
, respectively. Concerning the height of the roughness element, we took into account three different values:
![]() $h_{r}=[0.05,0.10,0.15]\,{\it\delta}_{99,L}$
, where
$h_{r}=[0.05,0.10,0.15]\,{\it\delta}_{99,L}$
, where
![]() ${\it\delta}_{99,L}$
is the thickness of the Blasius boundary layer at
${\it\delta}_{99,L}$
is the thickness of the Blasius boundary layer at
![]() $x=L$
. (Note that
$x=L$
. (Note that
![]() ${\it\delta}_{99,L}$
based on the Blasius solution is just a reference value. The corresponding values in terms of the compressible boundary-layer solutions are as follows: case 1,
${\it\delta}_{99,L}$
based on the Blasius solution is just a reference value. The corresponding values in terms of the compressible boundary-layer solutions are as follows: case 1,
![]() $h_{r}=[0.042,0.084,0.126]\,{\it\delta}_{99,L,comp}$
; case 2,
$h_{r}=[0.042,0.084,0.126]\,{\it\delta}_{99,L,comp}$
; case 2,
![]() $h_{r}=[0.039,0.078,0.118]\,{\it\delta}_{99,L,comp}$
.) The Reynolds number, defined as
$h_{r}=[0.039,0.078,0.118]\,{\it\delta}_{99,L,comp}$
.) The Reynolds number, defined as
was set equal to
![]() $4\times 10^{5}$
in all the tests performed, where,
$4\times 10^{5}$
in all the tests performed, where,
![]() ${\it\rho}_{\infty }$
denotes the free-stream density,
${\it\rho}_{\infty }$
denotes the free-stream density,
![]() $u_{\infty }$
is the free-stream velocity and
$u_{\infty }$
is the free-stream velocity and
![]() ${\it\mu}_{\infty }$
refers to the free-stream dynamic viscosity.
${\it\mu}_{\infty }$
refers to the free-stream dynamic viscosity.

Figure 1. Model problem.
A summary of the main parameters used for the numerical simulations is reported in table 1. Note that we applied isothermal boundary conditions to the flat plate surface, where the wall temperature was equal to the far-field temperature in the subsonic case, while it was calculated using the Crocco integral in the transonic case.
Table 1. Set of numerical simulations performed.
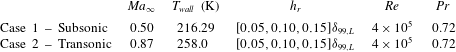
The Mach, Reynolds and Prandtl numbers were chosen to be relevant for aeronautical applications, while the shape and the related parameters can be seen as simple models of small imperfections at the leading edge of civil aircraft wings. In addition, the three hump heights explored range from a non-separated flow to a well-established separation bubble behind the obstacle. Note that, in this paper, we are mainly interested in the nonlinear regime; therefore, the case
![]() $h_{r}=0.05{\it\delta}_{99}$
was chosen such that it fell within a nonlinear regime without separation.
$h_{r}=0.05{\it\delta}_{99}$
was chosen such that it fell within a nonlinear regime without separation.
3. Theoretical and numerical approaches
3.1. Triple-deck formulation
The scales adopted in the triple-deck formulation are depicted in figure 2. Specifically, the subsonic case is represented in figure 2(a), while the transonic case is in figure 2(b). In the following, we briefly introduce the triple-deck formulation used in this paper.

Figure 2. Three-tiered structure of the interaction region for (a) the subsonic and (b) the transonic cases.
We first write the set of equations for the lower deck (see figure 2) in the canonical form
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle u_{0}\frac{\partial u_{0}}{\partial x_{0}}+v_{0}\frac{\partial u_{0}}{\partial y_{0}}=-\frac{\partial p_{0}}{\partial x_{0}}+\frac{\partial ^{2}u_{0}}{\partial y_{0}^{2}},\\ \displaystyle \frac{\partial u_{0}}{\partial x_{0}}+\frac{\partial v_{0}}{\partial y_{0}}=0,\end{array}\!\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle u_{0}\frac{\partial u_{0}}{\partial x_{0}}+v_{0}\frac{\partial u_{0}}{\partial y_{0}}=-\frac{\partial p_{0}}{\partial x_{0}}+\frac{\partial ^{2}u_{0}}{\partial y_{0}^{2}},\\ \displaystyle \frac{\partial u_{0}}{\partial x_{0}}+\frac{\partial v_{0}}{\partial y_{0}}=0,\end{array}\!\right\} & & \displaystyle\end{eqnarray}$$
with the conditions
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}ll@{}}u_{0}=v_{0}=0 & \text{at }y_{0}=0,\\ u_{0}=y_{0}+\cdots \, & \text{as }x_{0}\rightarrow -\infty ,\\ u_{0}=y_{0}+A_{0}(x)+\cdots \, & \text{as }y_{0}\rightarrow \infty ,\end{array}\!\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}ll@{}}u_{0}=v_{0}=0 & \text{at }y_{0}=0,\\ u_{0}=y_{0}+\cdots \, & \text{as }x_{0}\rightarrow -\infty ,\\ u_{0}=y_{0}+A_{0}(x)+\cdots \, & \text{as }y_{0}\rightarrow \infty ,\end{array}\!\right\} & & \displaystyle\end{eqnarray}$$
where
![]() $A_{0}(x)$
is the displacement function,
$A_{0}(x)$
is the displacement function,
![]() $x_{0}$
and
$x_{0}$
and
![]() $y_{0}$
are the streamwise and wall-normal coordinates,
$y_{0}$
are the streamwise and wall-normal coordinates,
![]() $u_{0}$
and
$u_{0}$
and
![]() $v_{0}$
are the associated velocities,
$v_{0}$
are the associated velocities,
![]() $p_{0}$
is the pressure and the subscript ‘0’ denotes leading-order dimensionless quantities, which are defined in the asymptotic expansions used and defined in §§ 3.1.1 and 3.1.2. The interaction law between the boundary layer (lower deck) and the potential flow in the upper deck has the form of a Hilbert integral for subsonic flows. In the transonic case, the interaction law is instead represented by the following integral:
$p_{0}$
is the pressure and the subscript ‘0’ denotes leading-order dimensionless quantities, which are defined in the asymptotic expansions used and defined in §§ 3.1.1 and 3.1.2. The interaction law between the boundary layer (lower deck) and the potential flow in the upper deck has the form of a Hilbert integral for subsonic flows. In the transonic case, the interaction law is instead represented by the following integral:
Here
![]() $F(x_{0})$
is the shape of the roughness element defined in § 2, and
$F(x_{0})$
is the shape of the roughness element defined in § 2, and
![]() $m$
is known as the Kármán–Guderley parameter (
$m$
is known as the Kármán–Guderley parameter (
![]() $m$
was equal to 1.3 in all the transonic cases taken into account) and is defined as
$m$
was equal to 1.3 in all the transonic cases taken into account) and is defined as
where
![]() $\mathit{Ma}_{\infty }$
is the free-stream Mach number. Note that in (3.3), for the transonic case, the upper-deck steady problem is described by the transonic small perturbation (TSP) equation disregarding the time derivative (for additional details, the interested reader can refer to Cole & Cook (Reference Cole and Cook1986)). In the subsonic case, the upper deck is instead solved through the Laplace equation for the pressure.
$\mathit{Ma}_{\infty }$
is the free-stream Mach number. Note that in (3.3), for the transonic case, the upper-deck steady problem is described by the transonic small perturbation (TSP) equation disregarding the time derivative (for additional details, the interested reader can refer to Cole & Cook (Reference Cole and Cook1986)). In the subsonic case, the upper deck is instead solved through the Laplace equation for the pressure.
To solve the steady triple-deck problem numerically, we discretise our two-dimensional domain with a set of mesh points at generic coordinates
![]() $(x_{0,i},y_{0,j})$
, where
$(x_{0,i},y_{0,j})$
, where
![]() $(i=1,\dots ,N_{x_{0}};~j=1,\dots ,N_{y_{0}})$
. Following Kravtsova, Zametaev & Ruban (Reference Kravtsova, Zametaev and Ruban2005), where the numerical approach adopted here is detailed, we define the displacement function vector
$(i=1,\dots ,N_{x_{0}};~j=1,\dots ,N_{y_{0}})$
. Following Kravtsova, Zametaev & Ruban (Reference Kravtsova, Zametaev and Ruban2005), where the numerical approach adopted here is detailed, we define the displacement function vector
![]() $\boldsymbol{A}_{0,i}$
and the pressure vector
$\boldsymbol{A}_{0,i}$
and the pressure vector
![]() $\boldsymbol{p}_{0,i}$
at each point
$\boldsymbol{p}_{0,i}$
at each point
![]() $x_{0,i}$
. The vectors
$x_{0,i}$
. The vectors
![]() $\boldsymbol{A}_{0,i}$
and
$\boldsymbol{A}_{0,i}$
and
![]() $\boldsymbol{p}_{0,i}$
define the values of the displacement function and of the pressure at all the points along the wall-normal direction
$\boldsymbol{p}_{0,i}$
define the values of the displacement function and of the pressure at all the points along the wall-normal direction
![]() $y_{0}$
. For a given displacement function
$y_{0}$
. For a given displacement function
![]() $\boldsymbol{A}_{0,i}$
, the interaction law in (3.3) (equivalently the interaction law for the subsonic case) allows the calculation of the inviscid pressure gradient
$\boldsymbol{A}_{0,i}$
, the interaction law in (3.3) (equivalently the interaction law for the subsonic case) allows the calculation of the inviscid pressure gradient
![]() $\text{d}\boldsymbol{p}_{0}/\text{d}x_{0}\big|_{inv}$
. For the same
$\text{d}\boldsymbol{p}_{0}/\text{d}x_{0}\big|_{inv}$
. For the same
![]() $\boldsymbol{A}_{0,i}$
, it is also possible to calculate the viscous pressure gradient
$\boldsymbol{A}_{0,i}$
, it is also possible to calculate the viscous pressure gradient
![]() $\text{d}\boldsymbol{p}_{0}/\text{d}x_{0}\big|_{v}$
by means of the lower-deck equations (3.1) and (3.2). The final set of implicit equations to be solved to find the displacement function
$\text{d}\boldsymbol{p}_{0}/\text{d}x_{0}\big|_{v}$
by means of the lower-deck equations (3.1) and (3.2). The final set of implicit equations to be solved to find the displacement function
![]() $\boldsymbol{A}_{0,i}$
is the difference between the inviscid and the viscous pressure gradients:
$\boldsymbol{A}_{0,i}$
is the difference between the inviscid and the viscous pressure gradients:
Equation (3.5) is solved using the Newton–Raphson method by iterating on the displacement function
![]() $\boldsymbol{A}_{0,i}$
. For additional details, the interested reader can also refer to Sychev et al. (Reference Sychev, Ruban, Sychev and Korolev1998).
$\boldsymbol{A}_{0,i}$
. For additional details, the interested reader can also refer to Sychev et al. (Reference Sychev, Ruban, Sychev and Korolev1998).
All the triple-deck calculations were performed using a second-order finite-difference method on an
![]() $801\times 301$
non-uniform mesh with minimum step sizes
$801\times 301$
non-uniform mesh with minimum step sizes
![]() ${\rm\Delta}x_{0}=0.005$
and
${\rm\Delta}x_{0}=0.005$
and
![]() ${\rm\Delta}y_{0}=0.005$
in the streamwise and wall-normal directions, respectively. Note that, to guarantee independence of the numerical results from the mesh resolution, we performed a mesh refinement study by using a finer grid (one order of magnitude greater resolution than the
${\rm\Delta}y_{0}=0.005$
in the streamwise and wall-normal directions, respectively. Note that, to guarantee independence of the numerical results from the mesh resolution, we performed a mesh refinement study by using a finer grid (one order of magnitude greater resolution than the
![]() ${\rm\Delta}x_{0}$
and
${\rm\Delta}x_{0}$
and
![]() ${\rm\Delta}y_{0}$
provided above). The difference in terms of
${\rm\Delta}y_{0}$
provided above). The difference in terms of
![]() $L^{\infty }$
-norm (normalised with respect to the respective absolute maximum values) between the results on the coarser and finer grids was less than 0.1 % for both the wall shear stress
$L^{\infty }$
-norm (normalised with respect to the respective absolute maximum values) between the results on the coarser and finer grids was less than 0.1 % for both the wall shear stress
![]() ${\it\tau}_{xy}$
and pressure gradient
${\it\tau}_{xy}$
and pressure gradient
![]() $\text{d}p/\text{d}x$
.
$\text{d}p/\text{d}x$
.
The asymptotic dimensionless expansions of the variables (denoted in (3.1) by the subscript ‘0’) used in the subsonic and transonic regimes are different and they are reported in the following two subsections.
3.1.1. Subsonic regime
If we consider the typical triple-deck scales around an isolated roughness element in the subsonic regime (figure 2 a), we can expand the streamwise and wall-normal directions as
where
![]() $x_{0}$
and
$x_{0}$
and
![]() $y_{0}$
indicate the dimensionless quantities used as asymptotic expansions in the triple-deck approach. Note that we have applied the Prandtl transposition theorem for the vertical coordinate and we have assumed that the hump was fully contained within the lower deck. Concerning the dimensional velocities
$y_{0}$
indicate the dimensionless quantities used as asymptotic expansions in the triple-deck approach. Note that we have applied the Prandtl transposition theorem for the vertical coordinate and we have assumed that the hump was fully contained within the lower deck. Concerning the dimensional velocities
![]() $(u,v)$
, we used the following asymptotic expansions:
$(u,v)$
, we used the following asymptotic expansions:
where
![]() $u_{0}$
and
$u_{0}$
and
![]() $v_{0}$
are the velocities related to the triple-deck approach. Finally, the dimensional thermodynamic quantities were expanded as follows:
$v_{0}$
are the velocities related to the triple-deck approach. Finally, the dimensional thermodynamic quantities were expanded as follows:
where
![]() ${\it\alpha}=\sqrt{1-\mathit{ Ma }_{\infty }^{2}}$
,
${\it\alpha}=\sqrt{1-\mathit{ Ma }_{\infty }^{2}}$
,
![]() $p$
is the pressure,
$p$
is the pressure,
![]() ${\it\rho}$
is the density and
${\it\rho}$
is the density and
![]() ${\it\mu}$
is the dynamic viscosity. Note that these variable transformations were used to compare DNS and triple-deck data in the subsonic case.
${\it\mu}$
is the dynamic viscosity. Note that these variable transformations were used to compare DNS and triple-deck data in the subsonic case.
3.1.2. Transonic regime
In the transonic regime (figure 2 b), the scales for the streamwise and wall-normal coordinates become
where, again, we have assumed that the hump was fully contained within the lower deck. Concerning the dimensional velocities
![]() $(u,v)$
, we used the following asymptotic expansions:
$(u,v)$
, we used the following asymptotic expansions:
Finally, the dimensional thermodynamic quantities assumed the same expressions as in the subsonic case, with the exception of the pressure, which was expanded as follows:
The Kármán–Guderley parameter was instead
Note that these variable transformations were used to compare DNS and triple-deck data in the transonic case.
3.2. Direct numerical simulation
The governing equations considered for the DNS are the unsteady two-dimensional compressible Navier–Stokes equations.
The spatial numerical discretisation adopted was a spectral/
![]() $hp$
element approach complemented by an explicit (in time) DG method. The temporal discretisation was an explicit fourth-order Runge–Kutta scheme. The spatial discretisation has an order of accuracy equal to
$hp$
element approach complemented by an explicit (in time) DG method. The temporal discretisation was an explicit fourth-order Runge–Kutta scheme. The spatial discretisation has an order of accuracy equal to
![]() $\mathscr{P}+1$
, where
$\mathscr{P}+1$
, where
![]() $\mathscr{P}$
is the order of the polynomials used within each element of the numerical grid.
$\mathscr{P}$
is the order of the polynomials used within each element of the numerical grid.
The numerical setting used is depicted in figure 3. We first simulated a flat plate with no roughness element as represented in figure 3, where we applied symmetry boundary conditions prior to the flat plate
![]() $AB$
, with
$AB$
, with
![]() $B$
representing the leading edge of the flat plate, which extends up to
$B$
representing the leading edge of the flat plate, which extends up to
![]() $C$
,
$C$
,
![]() $CD$
is the outflow region,
$CD$
is the outflow region,
![]() $DE$
is the far field and finally
$DE$
is the far field and finally
![]() $EA$
is the inflow. In generating the data on the flat plate, we run a sensitivity analysis regarding the position of the boundaries as well as a mesh refinement study in order to assure that the data produced were effectively independent of these factors. All the simulations were run until the steady state was reached. Note that we also verified that the boundary-layer profiles generated were consistent with those calculated by solving the compressible boundary-layer equations under the same conditions.
$EA$
is the inflow. In generating the data on the flat plate, we run a sensitivity analysis regarding the position of the boundaries as well as a mesh refinement study in order to assure that the data produced were effectively independent of these factors. All the simulations were run until the steady state was reached. Note that we also verified that the boundary-layer profiles generated were consistent with those calculated by solving the compressible boundary-layer equations under the same conditions.

Figure 3. DNS configuration.
After having obtained the data on the flat plate without roughness element, we interpolated these data in the embedded domain
![]() $Z_{1}Z_{2}Z_{3}Z_{4}$
around the roughness element represented in figure 3. The initial conditions and all the boundary conditions (except the no-slip boundary condition at the wall) were prescribed from the data obtained in the flat-plate simulations. Note that the boundary conditions were Dirichlet and they were imposed in a weak form. Also, for the embedded simulations, we performed a sensitivity study in order to assess the independence of the results from the boundary location as well as from the mesh resolution. The difference in terms of
$Z_{1}Z_{2}Z_{3}Z_{4}$
around the roughness element represented in figure 3. The initial conditions and all the boundary conditions (except the no-slip boundary condition at the wall) were prescribed from the data obtained in the flat-plate simulations. Note that the boundary conditions were Dirichlet and they were imposed in a weak form. Also, for the embedded simulations, we performed a sensitivity study in order to assess the independence of the results from the boundary location as well as from the mesh resolution. The difference in terms of
![]() $L^{\infty }$
-norm (normalised with respect to the respective absolute maximum values) between the finest mesh used and a mesh with approximately half of the resolution was less than 1 % for both the wall shear stress
$L^{\infty }$
-norm (normalised with respect to the respective absolute maximum values) between the finest mesh used and a mesh with approximately half of the resolution was less than 1 % for both the wall shear stress
![]() ${\it\tau}_{xy}$
and the pressure gradient
${\it\tau}_{xy}$
and the pressure gradient
![]() $\text{d}p/\text{d}x$
.
$\text{d}p/\text{d}x$
.
The final embedded mesh was constituted by
![]() $500\times 66$
elements, where we employed a stretching technique in both the wall-normal and the streamwise directions. We used a solution polynomial of order three within each element and, therefore, the number of solution points in the wall-normal direction was equal to 264 (220 of which were contained within the boundary layer at the roughness location), while that in the streamwise direction was equal to 2000. The minimum
$500\times 66$
elements, where we employed a stretching technique in both the wall-normal and the streamwise directions. We used a solution polynomial of order three within each element and, therefore, the number of solution points in the wall-normal direction was equal to 264 (220 of which were contained within the boundary layer at the roughness location), while that in the streamwise direction was equal to 2000. The minimum
![]() ${\rm\Delta}y$
in proximity to the wall was equal to
${\rm\Delta}y$
in proximity to the wall was equal to
![]() $2\times 10^{-6}~\text{m}$
. In the streamwise direction, the maximum resolution near the roughness element was equal to
$2\times 10^{-6}~\text{m}$
. In the streamwise direction, the maximum resolution near the roughness element was equal to
![]() $1\times 10^{-5}~\text{m}$
. The description of the roughness element was obtained using a fifth-order spline to achieve an accurate description of the geometry.
$1\times 10^{-5}~\text{m}$
. The description of the roughness element was obtained using a fifth-order spline to achieve an accurate description of the geometry.

Figure 4. Comparison of (a,c)
![]() $\text{d}p/\text{d}x$
and (b,d)
$\text{d}p/\text{d}x$
and (b,d)
![]() ${\it\tau}_{xy}$
(dimensional values) for (a,b) the 5 % and (c,d) the 15 % cases, with
${\it\tau}_{xy}$
(dimensional values) for (a,b) the 5 % and (c,d) the 15 % cases, with
![]() $\mathit{Ma}_{\infty }=0.50$
and
$\mathit{Ma}_{\infty }=0.50$
and
![]() $T_{wall}=T_{\infty }=216.29~\text{K}$
(case 1, subsonic).
$T_{wall}=T_{\infty }=216.29~\text{K}$
(case 1, subsonic).
4. Numerical results
The numerical simulations were performed at two different Mach numbers, the first subsonic,
![]() $\mathit{Ma}_{\infty }=0.5$
, and the second transonic,
$\mathit{Ma}_{\infty }=0.5$
, and the second transonic,
![]() $\mathit{Ma}_{\infty }=0.87$
. The shape of the roughness element is given in (2.1), where we used the parameters specified in § 2 and three different heights: 0.05
$\mathit{Ma}_{\infty }=0.87$
. The shape of the roughness element is given in (2.1), where we used the parameters specified in § 2 and three different heights: 0.05
![]() ${\it\delta}_{99}$
, 0.1
${\it\delta}_{99}$
, 0.1
![]() ${\it\delta}_{99}$
and 0.15
${\it\delta}_{99}$
and 0.15
![]() ${\it\delta}_{99}$
. We recall that
${\it\delta}_{99}$
. We recall that
![]() ${\it\delta}_{99}$
is a reference value and refers to the Blasius boundary layer at the roughness location.
${\it\delta}_{99}$
is a reference value and refers to the Blasius boundary layer at the roughness location.
The comparison between triple-deck and DNS simulations was carried out using two quantities: the pressure gradient along the streamwise direction
![]() $\text{d}p/\text{d}x$
, and the shear stress
$\text{d}p/\text{d}x$
, and the shear stress
![]() ${\it\tau}_{xy}$
. We also compared the difference between DNS and triple-deck theory in terms of the length of the separation bubbles (where present) as well as their detachment and reattachment points.
${\it\tau}_{xy}$
. We also compared the difference between DNS and triple-deck theory in terms of the length of the separation bubbles (where present) as well as their detachment and reattachment points.
In figure 4 we show the comparison of
![]() $\text{d}p/\text{d}x$
and
$\text{d}p/\text{d}x$
and
![]() ${\it\tau}_{xy}$
for case 1: Mach number
${\it\tau}_{xy}$
for case 1: Mach number
![]() $\mathit{Ma}_{\infty }=0.50$
, wall temperature
$\mathit{Ma}_{\infty }=0.50$
, wall temperature
![]() $T_{wall}=216.29~\text{K}$
and roughness element heights
$T_{wall}=216.29~\text{K}$
and roughness element heights
![]() $h_{r}=0.05{\it\delta}_{99}$
and
$h_{r}=0.05{\it\delta}_{99}$
and
![]() $h_{r}=0.15{\it\delta}_{99}$
, respectively. In figure 5 we show the same quantities for case 2: Mach number
$h_{r}=0.15{\it\delta}_{99}$
, respectively. In figure 5 we show the same quantities for case 2: Mach number
![]() $\mathit{Ma}_{\infty }=0.87$
, wall temperature
$\mathit{Ma}_{\infty }=0.87$
, wall temperature
![]() $T_{wall}=258.0~\text{K}$
(see also table 1). From these figures it is possible to see an overall good agreement between triple-deck and DNS data except in proximity to the centre of the roughness element, where large discrepancies are observed (as can be seen from the inset images, which are a close-up view of this region). These discrepancies are expected in the asymptotic analysis because in proximity to the roughness element we observed a larger acceleration of the flow in the DNS results when compared to the triple-deck data. Also, the deceleration of the flow behind the hump is larger in the DNS data when compared to the triple-deck one. These features generate sharper and higher peaks in terms of both wall shear stress
$T_{wall}=258.0~\text{K}$
(see also table 1). From these figures it is possible to see an overall good agreement between triple-deck and DNS data except in proximity to the centre of the roughness element, where large discrepancies are observed (as can be seen from the inset images, which are a close-up view of this region). These discrepancies are expected in the asymptotic analysis because in proximity to the roughness element we observed a larger acceleration of the flow in the DNS results when compared to the triple-deck data. Also, the deceleration of the flow behind the hump is larger in the DNS data when compared to the triple-deck one. These features generate sharper and higher peaks in terms of both wall shear stress
![]() ${\it\tau}_{xy}$
and longitudinal pressure gradient
${\it\tau}_{xy}$
and longitudinal pressure gradient
![]() $\text{d}p/\text{d}x$
. We also observed that the wall-normal pressure gradient in the DNS data has a contribution that is neglected in the triple-deck theory and might affect the behaviour of the two quantities investigated and contribute to the discrepancies seen, although some other factors may also play a role.
$\text{d}p/\text{d}x$
. We also observed that the wall-normal pressure gradient in the DNS data has a contribution that is neglected in the triple-deck theory and might affect the behaviour of the two quantities investigated and contribute to the discrepancies seen, although some other factors may also play a role.

Figure 5. Comparison of (a,c)
![]() $\text{d}p/\text{d}x$
and (b,d)
$\text{d}p/\text{d}x$
and (b,d)
![]() ${\it\tau}_{xy}$
(dimensional values) for (a,b) the 5 % and (c,d) the 15 % cases, with
${\it\tau}_{xy}$
(dimensional values) for (a,b) the 5 % and (c,d) the 15 % cases, with
![]() $\mathit{Ma}_{\infty }=0.87$
and
$\mathit{Ma}_{\infty }=0.87$
and
![]() $T_{wall}=258.0~\text{K}$
(case 2, transonic).
$T_{wall}=258.0~\text{K}$
(case 2, transonic).
In table 2 we quantified the differences between DNS and triple-deck data at four distinct locations along the streamwise direction,
![]() $\text{P}1=0.046~\text{m}$
,
$\text{P}1=0.046~\text{m}$
,
![]() $\text{P}2=0.049~\text{m}$
,
$\text{P}2=0.049~\text{m}$
,
![]() $\text{P}3=0.051~\text{m}$
and
$\text{P}3=0.051~\text{m}$
and
![]() $\text{P}4=0.054~\text{m}$
, for both the wall shear stress
$\text{P}4=0.054~\text{m}$
, for both the wall shear stress
![]() ${\it\tau}_{xy}$
and the longitudinal pressure gradient
${\it\tau}_{xy}$
and the longitudinal pressure gradient
![]() $\text{d}p/\text{d}x$
. We also measured the maximum difference between DNS and triple-deck data (reported in the last column of the table). All the differences are normalised with respect to the maximum absolute value obtained in the DNS results for each case considered. We can see how the difference between DNS and triple-deck data in terms of
$\text{d}p/\text{d}x$
. We also measured the maximum difference between DNS and triple-deck data (reported in the last column of the table). All the differences are normalised with respect to the maximum absolute value obtained in the DNS results for each case considered. We can see how the difference between DNS and triple-deck data in terms of
![]() $\text{d}p/\text{d}x$
and
$\text{d}p/\text{d}x$
and
![]() ${\it\tau}_{xy}$
in proximity to the hump (points P2, P3 and maximum difference) increases as the height of the roughness element increases in both subsonic and transonic regimes. In particular, we estimated that the maximum difference in terms of
${\it\tau}_{xy}$
in proximity to the hump (points P2, P3 and maximum difference) increases as the height of the roughness element increases in both subsonic and transonic regimes. In particular, we estimated that the maximum difference in terms of
![]() $\text{d}p/\text{d}x$
in proximity to the centre of the roughness element was between 27 % (for
$\text{d}p/\text{d}x$
in proximity to the centre of the roughness element was between 27 % (for
![]() $h_{r}=0.05{\it\delta}_{99}$
, subsonic case) and more than 54 % (for
$h_{r}=0.05{\it\delta}_{99}$
, subsonic case) and more than 54 % (for
![]() $h_{r}=0.15{\it\delta}_{99}$
, transonic case), while moving slightly off from the roughness centre these differences were consistently lower with an order of magnitude below 2 %. The maximum differences in terms of
$h_{r}=0.15{\it\delta}_{99}$
, transonic case), while moving slightly off from the roughness centre these differences were consistently lower with an order of magnitude below 2 %. The maximum differences in terms of
![]() ${\it\tau}_{xy}$
were between 11 % and 30 % (also in this case normalised with respect to the maximum absolute value of
${\it\tau}_{xy}$
were between 11 % and 30 % (also in this case normalised with respect to the maximum absolute value of
![]() ${\it\tau}_{xy}$
obtained from the DNS data) in proximity to the centre of the roughness element. These differences consistently decreased moving either upstream or downstream, with maximum differences in these regions below 4 %.
${\it\tau}_{xy}$
obtained from the DNS data) in proximity to the centre of the roughness element. These differences consistently decreased moving either upstream or downstream, with maximum differences in these regions below 4 %.
Table 2. Difference between DNS and triple-deck theory in the
![]() $\text{d}p/\text{d}x$
and
$\text{d}p/\text{d}x$
and
![]() ${\it\tau}_{xy}$
variables normalised with respect to their maximum absolute values obtained from the DNS data at four different locations along the flat plate:
${\it\tau}_{xy}$
variables normalised with respect to their maximum absolute values obtained from the DNS data at four different locations along the flat plate:
![]() $\text{P}1=0.046~\text{m}$
,
$\text{P}1=0.046~\text{m}$
,
![]() $\text{P}2=0.049~\text{m}$
,
$\text{P}2=0.049~\text{m}$
,
![]() $\text{P}3=0.051~\text{m}$
,
$\text{P}3=0.051~\text{m}$
,
![]() $\text{P}4=0.054~\text{m}$
. The last value is the maximum difference between DNS and triple-deck data, also normalised with respect to the DNS maximum absolute value.
$\text{P}4=0.054~\text{m}$
. The last value is the maximum difference between DNS and triple-deck data, also normalised with respect to the DNS maximum absolute value.

In table 3 we quantified the differences in terms of separation bubble lengths, and the differences in terms of detachment (
![]() $D$
) and reattachment (
$D$
) and reattachment (
![]() $R$
) points between DNS and triple-deck results. These differences are normalised with respect to the length
$R$
) points between DNS and triple-deck results. These differences are normalised with respect to the length
![]() $\ell _{999}$
of the hump (we considered a tolerance
$\ell _{999}$
of the hump (we considered a tolerance
![]() $\mathscr{T}=0.001h_{r}$
at which we measured the length of the hump; this gave us
$\mathscr{T}=0.001h_{r}$
at which we measured the length of the hump; this gave us
![]() $\ell _{999}\approx 0.00096~\text{m}$
).
$\ell _{999}\approx 0.00096~\text{m}$
).
Table 3. Difference between DNS and triple-deck theory in terms of the detachment point (D), reattachment point (R) and length (
![]() $\mathscr{L}$
) of the separation bubbles – normalised quantities.
$\mathscr{L}$
) of the separation bubbles – normalised quantities.

It is possible to note that the underlying qualitative physics of the problem is well captured by both approaches. In particular, separation happens for the same test cases in both DNS and triple-deck theory. The differences in terms of detachment point is relatively contained (less than 6 % for
![]() $h_{r}=0.10{\it\delta}_{99}$
in the subsonic case, and less than 3 % for
$h_{r}=0.10{\it\delta}_{99}$
in the subsonic case, and less than 3 % for
![]() $h_{r}=0.15{\it\delta}_{99}$
in the subsonic and transonic cases). The major gap between the two approaches is related to the reattachment point, which in turn influences the length of the separation bubble. We note that this gap increases as the height of the hump increases. This is probably related to the local behaviour of the pressure in proximity and prior to the reattachment point. In fact, in the DNS results we observe a larger streamwise pressure gradient in proximity to and behind the hump when compared to the triple-deck theory. Also, the wall-normal pressure gradient is not negligible in this region. Both the streamwise and wall-normal pressure gradients strongly influence the deceleration of the flow and therefore the position of the reattachment point; see, for example, Stewartson (Reference Stewartson1970) and Korolev, Gajjar & Ruban (Reference Korolev, Gajjar and Ruban2002).
$h_{r}=0.15{\it\delta}_{99}$
in the subsonic and transonic cases). The major gap between the two approaches is related to the reattachment point, which in turn influences the length of the separation bubble. We note that this gap increases as the height of the hump increases. This is probably related to the local behaviour of the pressure in proximity and prior to the reattachment point. In fact, in the DNS results we observe a larger streamwise pressure gradient in proximity to and behind the hump when compared to the triple-deck theory. Also, the wall-normal pressure gradient is not negligible in this region. Both the streamwise and wall-normal pressure gradients strongly influence the deceleration of the flow and therefore the position of the reattachment point; see, for example, Stewartson (Reference Stewartson1970) and Korolev, Gajjar & Ruban (Reference Korolev, Gajjar and Ruban2002).
Although the gap is related to the reattachment point and therefore to the length of the separation bubble, we consider the agreement between the two approaches satisfactory.
5. Summary and conclusions
In this paper we compared two substantially different approaches, namely DNS and asymptotic triple-deck theory, for calculating the flow past an isolated roughness element on a flat plate with separation behind the element in some situations. The calculations were performed in a compressible regime, and both subsonic and transonic conditions were taken into account. We considered three different roughness element heights, ranging from a non-separated flow to a laminar separation bubble behind the obstacle. The study has been carried out by comparing two quantities, the pressure gradient
![]() $\text{d}p/\text{d}x$
and the shear stress
$\text{d}p/\text{d}x$
and the shear stress
![]() ${\it\tau}_{xy}$
, as well as by evaluating the location of the detachment and reattachment points and the length of the separation bubble where present.
${\it\tau}_{xy}$
, as well as by evaluating the location of the detachment and reattachment points and the length of the separation bubble where present.
The results obtained for
![]() $\text{d}p/\text{d}x$
and
$\text{d}p/\text{d}x$
and
![]() ${\it\tau}_{xy}$
show an overall good agreement between DNS and triple-deck data except for their maximum and minimum values. This behaviour can be expected since we observe a non-zero wall-normal pressure gradient in the DNS data when compared to the triple-deck results (where a zero pressure gradient along the wall-normal direction is assumed) and a different flow acceleration/deceleration in proximity to the hump between triple-deck and DNS data. This aspect can well affect the local behaviour of the wall shear stress and of the longitudinal pressure gradient, even though some other nonlinear effects can also contribute to the differences observed. In addition, triple-deck theory relies on the assumption that
${\it\tau}_{xy}$
show an overall good agreement between DNS and triple-deck data except for their maximum and minimum values. This behaviour can be expected since we observe a non-zero wall-normal pressure gradient in the DNS data when compared to the triple-deck results (where a zero pressure gradient along the wall-normal direction is assumed) and a different flow acceleration/deceleration in proximity to the hump between triple-deck and DNS data. This aspect can well affect the local behaviour of the wall shear stress and of the longitudinal pressure gradient, even though some other nonlinear effects can also contribute to the differences observed. In addition, triple-deck theory relies on the assumption that
![]() $\mathit{Re}$
is large; therefore we expect a better agreement if we increase
$\mathit{Re}$
is large; therefore we expect a better agreement if we increase
![]() $\mathit{Re}$
, although the Reynolds number adopted in this work is relevant for aeronautical applications. It is also possible to note that the discrepancy between DNS and triple-deck data increases as the height of the roughness element increases, and therefore when nonlinear effects become more relevant (see table 2 for example).
$\mathit{Re}$
, although the Reynolds number adopted in this work is relevant for aeronautical applications. It is also possible to note that the discrepancy between DNS and triple-deck data increases as the height of the roughness element increases, and therefore when nonlinear effects become more relevant (see table 2 for example).
Concerning the separation bubbles, both DNS and triple-deck theory predict separation for the same test cases. This indicates that the underlying physics of the problem is well captured in both approaches (in the limit of two-dimensional separation bubbles). Specifically, the detachment point compares well, though some rather large differences are present for the reattachment point, probably due to the different longitudinal and wall-normal pressure distributions between DNS and triple-deck data.
This study demonstrates that the asymptotic triple-deck theory captures correctly the qualitative physics and the main flow features in practical aeronautical applications, and therefore it can be effectively used as a reduced model in this field. This is of particular use in estimates of receptivity and in separation prediction studies, where the quantities we have investigated,
![]() $\text{d}p/\text{d}x$
and
$\text{d}p/\text{d}x$
and
![]() ${\it\tau}_{xy}$
, are very relevant; see, for example, Rizzetta, Burggraf & Jenson (Reference Rizzetta, Burggraf and Jenson1978) and Ruban, Bernots & Pryce (Reference Ruban, Bernots and Pryce2013). (Note that the velocity profiles are also important for stability and receptivity calculations. However, the two quantities investigated in this paper, i.e.
${\it\tau}_{xy}$
, are very relevant; see, for example, Rizzetta, Burggraf & Jenson (Reference Rizzetta, Burggraf and Jenson1978) and Ruban, Bernots & Pryce (Reference Ruban, Bernots and Pryce2013). (Note that the velocity profiles are also important for stability and receptivity calculations. However, the two quantities investigated in this paper, i.e.
![]() $\text{d}p/\text{d}x$
and
$\text{d}p/\text{d}x$
and
![]() ${\it\tau}_{xy}$
, provide a satisfactory insight into the separation characteristics of the flow and they can be used for receptivity studies.)
${\it\tau}_{xy}$
, provide a satisfactory insight into the separation characteristics of the flow and they can be used for receptivity studies.)
On the other hand, from a quantitative perspective, the triple-deck theory is not entirely reliable when considering a nonlinear regime and its use in this context has to be considered carefully, especially if accurate quantitative calculations are required.
This work also constitutes the rationale for further studies on the connections between the two approaches, historically developed in two different research communities, and it allows a more theoretical insight into the DNS data as well as a more applied viewpoint for the triple-deck community.
Acknowledgements
We thank Dr T. Bernots for helpful discussions and Dr H. Xu for his useful comments on the DNS calculations. This work was supported by the Laminar Flow Control Centre funded by Airbus/EADS and EPSRC under grant EP/I037946.