Hostname: page-component-8448b6f56d-dnltx Total loading time: 0 Render date: 2024-04-23T17:07:19.427Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulence at the Lee bound: maximally non-normal vortex filaments and the decay of a local dissipation rate

Published online by Cambridge University Press:  24 October 2019

Christopher J. Keylock Open the ORCID record for Christopher J. Keylock [Opens in a new window]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper uses a tight mathematical bound on the degree of the non-normality of the turbulent velocity gradient tensor to classify flow behaviour within vortical regions (where the eigenvalues of the tensor contain a conjugate pair). Structures attaining this bound are preferentially generated where enstrophy exceeds total strain and there is a positive balance between strain production and enstrophy production. Lagrangian analysis of homogeneous, isotropic turbulence shows that attainment of this bound is associated with relatively short durations and an upper limit to the spatial extent of the flow structures that is similar to the Taylor scale. An analysis of the dynamically relevant terms using a recently developed formulation (Keylock, J. Fluid Mech., vol. 848, 2018, pp. 876–904), highlights the controls on this dynamics. In particular, in high enstrophy regions it is shown that the bound is attained when normal strain decreases rather than when non-normality increases. The near absence of normal total strain results in a source of intermittency in the dynamics of dissipation that is hidden in standard analyses. It is shown that of the two terms that contribute to the non-normal production dynamics, it is the one that is typically smallest in magnitude that is of greatest importance within these 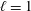$\ell =1$ filaments. The typical distance between filament centroids is just less than a Taylor scale, implying a connection to the manner in which flow topology at the Taylor scale explains dissipation at smaller scales.

JFM classification

Vortex Flows: Vortex dynamics Turbulent Flows: Turbulence theory Turbulent Flows: Isotropic turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 881 , 25 December 2019 , pp. 283 - 312
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ashurst, W. T., Kerstein, A. R., Kerr, R. A. & Gibson, C. H. 1987 Alignment of vorticity and scalar gradient with strain rate in simulated Navier–Stokes turbulence. Phys. Fluids 30, 2343–2353.10.1063/1.866513Google Scholar
Ballouz, J. G. & Ouellette, N. T. 2018 Tensor geometry in the turbulent cascade. J. Fluid Mech. 835, 1048–1064.10.1017/jfm.2017.802Google Scholar
Batchelor, G. K. & Townsend, A. A. 1949 The nature of turbulent motion at large wave-numbers. Proc. R. Soc. Lond. A 199, 238–255.Google Scholar
Betchov, R. 1956 An inequality concerning the production of vorticity in isotropic turbulence. J. Fluid Mech. 1, 497–504.10.1017/S0022112056000317Google Scholar
Biferale, L., Chevillard, L., Meneveau, C. & Toschi, F. 2007 Multiscale model of gradient evolution in turbulent flows. Phys. Rev. Lett. 98, 214501.10.1103/PhysRevLett.98.214501Google Scholar
Buxton, O. R. H., Breda, M. & Chen, X. 2017 Invariants of the velocity-gradient tensor in a spatially developing inhomogeneous turbulent flow. J. Fluid Mech. 817, 1–20.10.1017/jfm.2017.93Google Scholar
Cantwell, B. J. 1992 Exact solution of a restricted Euler equation for the velocity gradient tensor. Phys. Fluids A 4 (4), 782–793.10.1063/1.858295Google Scholar
Chakraborty, P., Balachandar, S. & Adrian, R. J. 2005 On the relationships between local vortex identification schemes. J. Fluid Mech. 535, 189–214.10.1017/S0022112005004726Google Scholar
Chevillard, L., Meneveau, C., Biferale, L. & Toschi, F. 2008 Modeling the pressure Hessian and viscous Laplacian in turbulence: comparisons with direct numerical simulation and implications on velocity gradient dynamics. Phys. Fluids 20, 101504.10.1063/1.3005832Google Scholar
Chong, M. S., Perry, A. E. & Cantwell, B. J. 1990 A general classification of three-dimensional flow fields. Phys. Fluids A 2, 765–777.10.1063/1.857730Google Scholar
Das, R. & Girimaji, S. S. 2019 On the Reynolds number dependence of velocity-gradient structure and dynamics. J. Fluid Mech. 861, 163–179.10.1017/jfm.2018.924Google Scholar
Dong, X., Gao, Y. & Liu, C. 2019 New normalized Rortex/vortex identification method. Phys. Fluids 31, 011701.10.1063/1.5066016Google Scholar
Dubief, Y. & Delcayre, F. 2000 On coherent-vortex identification in turbulence. J. Turbul. 1, N11.Google Scholar
Eberlein, P. J. 1965 On measures of non-normality for matrices. Amer. Math. Monthly 72, 995–996.10.2307/2313341Google Scholar
Elsinga, G. E. & Marusic, I. 2010 Universal aspects of small-scale motions in turbulence. J. Fluid Mech. 662, 514–539.10.1017/S0022112010003381Google Scholar
Frisch, U., Sulem, P. L. & Nelkin, M. 1978 Simple dynamical model of intermittent fully developed turbulence. J. Fluid Mech. 87, 719–736.10.1017/S0022112078001846Google Scholar
George, W. K. 1992 The decay of homogeneous isotropic turbulence. Phys. Fluids A 4, 1492–1509.10.1063/1.858423Google Scholar
Girimaji, S. S. & Pope, S. B. 1990 A diffusion model for velocity gradients in turbulence. Phys. Fluids 2 (2), 242–256.10.1063/1.857773Google Scholar
Gomes-Fernandes, R., Ganapathisubramani, B. & Vassilicos, J. C. 2014 Evolution of the velocity-gradient tensor in a spatially developing turbulent flow. J. Fluid Mech. 756, 252–292.10.1017/jfm.2014.452Google Scholar
Goto, S. & Vassilicos, J. C. 2009 The dissipation rate coefficient of turbulence is not universal and depends on the internal stagnation point structure. Phys. Fluids 21, 035104.10.1063/1.3085721Google Scholar
Hamlington, P. E., Schumacher, J. & Dahm, W. J. A. 2008 Direct assessment of vorticity alignment with local and nonlocal strain rates in turbulent flows. Phys. Fluids 20, 111703.10.1063/1.3021055Google Scholar
Henrici, P. 1962 Bounds for iterates, inverses, spectral variation and fields of values of non-normal matrices. Numer. Math. 4, 24–40.10.1007/BF01386294Google Scholar
Horiuti, K. 2001 A classification method for vortex sheet and tube structures in turbulent flows. Phys. Fluids 13, 3756–3774.10.1063/1.1410981Google Scholar
Horiuti, K., Yanagihara, S. & Tamaki, T. 2016 Nonequilibrium state in energy spectra and transfer with implications for topological transitions and SGS modeling. Fluid Dyn. Res. 48, 021409.Google Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P.1988 Eddies, stream, and convergence zones in turbulent flows. Tech. Rep. CTR-S88. Center for Turbulence Research, Stanford University.Google Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.10.1017/S0022112095000462Google Scholar
Jimenez, J., Wray, A. A., Saffman, P. G. & Rogallo, R. S. 1993 The structure of intense vorticity in homogeneous isotropic turbulence. J. Fluid Mech. 255, 65–90.10.1017/S0022112093002393Google Scholar
Johnson, P. L. & Meneveau, C. 2016 A closure for Lagrangian velocity gradient evolution in turbulence using recent-deformation mapping of initially Gaussian fields. J. Fluid Mech. 804, 387–419.10.1017/jfm.2016.551Google Scholar
Kawahara, G. 2005 Energy dissipation in spiral vortex layers wrapped around a straight vortex tube. Phys. Fluids 17, 055111.10.1063/1.1897011Google Scholar
Kerr, R. M. 1985 Higher-order derivative correlations and the alignment of small-scale structures in isotropic, numerical turbulence. J. Fluid Mech. 153, 31–58.10.1017/S0022112085001136Google Scholar
Keylock, C. J. 2017 Synthetic velocity gradient tensors and the identification of statistically significant aspects of the structure of turbulence. Phys. Rev. Fluids 2, 004600.Google Scholar
Keylock, C. J. 2018 The Schur decomposition of the velocity gradient tensor for turbulent flows. J. Fluid Mech. 848, 876–904.10.1017/jfm.2018.344Google Scholar
Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 299–303.Google Scholar
Kolmogorov, A. N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous, incompressible fluid at high Reynolds number. J. Fluid Mech. 13, 82–85.10.1017/S0022112062000518Google Scholar
Kress, R., De Vies, H. L. & Wegmann, R. 1974 On nonnormal matrices. Linear Algebr. Applics. 8, 109–120.10.1016/0024-3795(74)90049-4Google Scholar
Laizet, S., Nedić, J. & Vassilicos, C. 2015 Influence of the spatial resolution on fine-scale features in DNS of turbulence generated by a single square grid. Intl J. Comput. Fluid Dyn. 29 (3-5), 286–302.Google Scholar
Laizet, S., Vassilicos, J. C. & Cambon, C. 2013 Interscale energy transfer in decaying turbulence and vorticity-strain-rate dynamics in grid-generated turbulence. Fluid Dyn. Res. 45 (6), 061408.Google Scholar
Lashermes, B., Roux, S. G., Abry, P. & Jaffard, S. 2008 Comprehensive multifractal analysis of turbulent velocity using the wavelet leaders. Eur. Phys. J. B 61, 201–215.Google Scholar
Lee, S. L. 1995 A practical upper bound for departure from normality. SIAM J. Matrix Anal. Applics. 16, 462–468.10.1137/S0895479893255184Google Scholar
Li, Y. & Meneveau, C. 2007 Material deformation in a restricted Euler model for turbulent flows: analytic solution and numerical tests. Phys. Fluids 19, 015104.10.1063/1.2432913Google Scholar
Li, Y., Perlman, E., Wan, M., Yang, Y., Burns, R., Meneveau, C., Chen, S., Szalay, A. & Eyink, G. 2008 A public turbulence database cluster and applications to study Lagrangian evolution of velocity increments in turbulence. J. Turbul. 9, N31.Google Scholar
Lück, S., Renner, C., Peinke, J. & Friedrich, R. 2006 The Markov–Einstein coherence length – a new meaning for the Taylor length in turbulence. Phys. Lett. A 359, 335–338.10.1016/j.physleta.2006.06.053Google Scholar
Lund, T. S. & Rogers, M. M. 1994 An improved measure of strain state probability in turbulent flows. Phys. Fluids 6 (5), 1838–1847.Google Scholar
Lüthi, B., Holzner, M. & Tsinober, A. 2009 Expanding the Q–R space to three dimensions. J. Fluid Mech. 641, 497–507.10.1017/S0022112009991947Google Scholar
Martin, J., Dopazo, C. & Valiño, L. 1998 Dynamics of velocity gradient invariants in turbulence: restricted Euler and linear diffusion models. Phys. Fluids 10, 2012–2025.10.1063/1.869717Google Scholar
Meneveau, C. 2011 Lagrangian dynamics and models of the velocity gradient tensor in turbulent flows. Annu. Rev. Fluid Mech. 43, 219–245.10.1146/annurev-fluid-122109-160708Google Scholar
Meneveau, C. & Sreenivasan, K. R. 1987 Simple multifractal cascade model for fully developed turbulence. Phys. Rev. Lett. 59, 1424–1427.10.1103/PhysRevLett.59.1424Google Scholar
Ohkitani, K. 2002 Numerical study of comparison of vorticity and passive vectors in turbulence and inviscid flows. Phys. Rev. E 65 (4), 046304.Google Scholar
Ohkitani, K. & Kishiba, S. 1995 Nonlocal nature of vortex stretching in an inviscid fluid. Phys. Fluids 7 (2), 411–421.10.1063/1.868638Google Scholar
Paul, I., Papadakis, G. & Vassilicos, J. C. 2017 Genesis and evolution of velocity gradients in near-field spatially developing turbulence. J. Fluid Mech. 815, 295–332.Google Scholar
Rabey, P. K., Wynn, A. & Buxton, O. R. H. 2015 The kinematics of the reduced velocity gradient tensor in a fully developed turbulent free shear flow. J. Fluid Mech. 767, 627–658.10.1017/jfm.2015.60Google Scholar
Schur, I. 1909 Über die charakteristischen Wurzeln einer linearen Substitution mit einer Anwendung auf die Theorie der Integralgleichungen. Math. Ann. 66, 488–510.Google Scholar
Taylor, G. I. 1935 Statistical theory of turbulence. Proc. R. Soc. Lond. A 151, 421–444.Google Scholar
Taylor, G. I. 1938a Production and dissipation of vorticity in a turbulent fluid. Proc. R. Soc. Lond. A 164, 15–23.Google Scholar
Taylor, G. I. 1938b The spectrum of turbulence. Proc. R. Soc. Lond. A 164, 476–490.Google Scholar
Tsinober, A. 2001 Vortex stretching versus production of strain/dissipation. In Turbulence Structure and Vortex Dynamics (ed. Hunt, J. C. R. & Vassilicos, J. C.), pp. 164–191. Cambridge University Press.Google Scholar
Tsinober, A. 2009 An Informal Conceptual Introduction to Turbulence. Springer.10.1007/978-90-481-3174-7Google Scholar
Tsinober, A., Shtilman, L. & Vaisburd, H. 1997 A study of properties of vortex stretching and enstrophy generation in numerical and laboratory turbulence. Fluid Dyn. Res. 21, 477–494.10.1016/S0169-5983(97)00022-1Google Scholar
Vieillefosse, P. 1984 Internal motion of a small element of fluid in an inviscid flow. Physica A 125, 150–162.10.1016/0378-4371(84)90008-6Google Scholar
Wan, M., Chen, S., Eyink, G., Meneveau, C., Perlman, E., Burns, R., Li, Y., Szalay, A. & Hamilton, S.2016 Johns Hopkins Turbulence Database (JHTDB). http://turbulence.pha.jhu.edu/datasets.aspx.Google Scholar
Wan, M., Xiao, Z., Meneveau, C., Eyink, G. L. & Chen, S. 2010 Dissipation-energy flux correlations as evidence for the Lagrangian energy cascade in turbulence. Phys. Fluids 22 (6), 1–4.10.1063/1.3447887Google Scholar
Wilczek, M. & Meneveau, C. 2014 Pressure Hessian and viscous contributions to velocity gradient statistics based on Gaussian random fields. J. Fluid Mech. 756, 191–225.10.1017/jfm.2014.367Google Scholar
Yakhot, V. 2003 Pressure-velocity correlations and scaling exponents in turbulence. J. Fluid Mech. 495, 135–143.10.1017/S0022112003006281Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices. J. Fluid Mech. 387, 353–396.10.1017/S002211209900467XGoogle Scholar
Zhou, Y., Nagata, K., Sakai, Y., Ito, Y. & Hayase, T. 2016 Spatial evolution of the helical behavior and the 2/3 power-law in single-square-grid-generated turbulence. Fluid Dyn. Res. 48 (2), 0214042.Google Scholar