Article contents
Turbulence during the reflection of internal gravity waves at critical and near-critical slopes
Published online by Cambridge University Press: 19 July 2013
Abstract
Direct numerical simulation is performed with a focus on the characterization of nonlinear dynamics during reflection of a plane internal wave at a sloping bottom. The effect of incoming wave amplitude is assessed by varying the incoming Froude number, 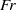 $Fr$ , and the effect of off-criticality is assessed by varying the slope angle in a range of near-critical values. At low
$Fr$ , and the effect of off-criticality is assessed by varying the slope angle in a range of near-critical values. At low 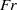 $\mathit{Fr}$ , the numerical results agree well with linear inviscid theory of near-critical internal wave reflection. With increasing
$\mathit{Fr}$ , the numerical results agree well with linear inviscid theory of near-critical internal wave reflection. With increasing 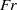 $\mathit{Fr}$ , the reflection process becomes nonlinear with the formation of higher harmonics and the initiation of fine-scale turbulence during the evolution of the reflected wave. Later in time, the wave response becomes quasi-steady with a systematic dependence of turbulence on the temporal and spatial phase. Convective instabilities are found to play a crucial role in the formation of turbulence during each cycle. The cycle evolution of flow statistics is studied in detail and qualitative differences between off-critical and critical reflection are identified. The parametric dependence of turbulence levels on Froude number and slope angle is calculated. Interestingly, at a given value of
$\mathit{Fr}$ , the reflection process becomes nonlinear with the formation of higher harmonics and the initiation of fine-scale turbulence during the evolution of the reflected wave. Later in time, the wave response becomes quasi-steady with a systematic dependence of turbulence on the temporal and spatial phase. Convective instabilities are found to play a crucial role in the formation of turbulence during each cycle. The cycle evolution of flow statistics is studied in detail and qualitative differences between off-critical and critical reflection are identified. The parametric dependence of turbulence levels on Froude number and slope angle is calculated. Interestingly, at a given value of 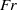 $\mathit{Fr}$ , the turbulent kinetic energy (TKE) can be higher for somewhat off-critical reflection compared to exactly critical reflection. For a fixed slope angle, as the Froude number increases in the simulated cases, the fraction of the input wave energy converted into the turbulent kinetic energy and the fraction of the input wave power dissipated by turbulence also increase.
$\mathit{Fr}$ , the turbulent kinetic energy (TKE) can be higher for somewhat off-critical reflection compared to exactly critical reflection. For a fixed slope angle, as the Froude number increases in the simulated cases, the fraction of the input wave energy converted into the turbulent kinetic energy and the fraction of the input wave power dissipated by turbulence also increase.
Information
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 15
- Cited by

