Article contents
Turbulence dynamics near a turbulent/non-turbulent interface
Published online by Cambridge University Press: 13 February 2012
Abstract
The characteristics of the boundary layer separating a turbulence region from an irrotational (or non-turbulent) flow region are investigated using rapid distortion theory (RDT). The turbulence region is approximated as homogeneous and isotropic far away from the bounding turbulent/non-turbulent (T/NT) interface, which is assumed to remain approximately flat. Inviscid effects resulting from the continuity of the normal velocity and pressure at the interface, in addition to viscous effects resulting from the continuity of the tangential velocity and shear stress, are taken into account by considering a sudden insertion of the T/NT interface, in the absence of mean shear. Profiles of the velocity variances, turbulent kinetic energy (TKE), viscous dissipation rate ( ), turbulence length scales, and pressure statistics are derived, showing an excellent agreement with results from direct numerical simulations (DNS). Interestingly, the normalized inviscid flow statistics at the T/NT interface do not depend on the form of the assumed TKE spectrum. Outside the turbulent region, where the flow is irrotational (except inside a thin viscous boundary layer),
), turbulence length scales, and pressure statistics are derived, showing an excellent agreement with results from direct numerical simulations (DNS). Interestingly, the normalized inviscid flow statistics at the T/NT interface do not depend on the form of the assumed TKE spectrum. Outside the turbulent region, where the flow is irrotational (except inside a thin viscous boundary layer),  decays as
decays as 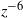 , where
, where  is the distance from the T/NT interface. The mean pressure distribution is calculated using RDT, and exhibits a decrease towards the turbulence region due to the associated velocity fluctuations, consistent with the generation of a mean entrainment velocity. The vorticity variance and
is the distance from the T/NT interface. The mean pressure distribution is calculated using RDT, and exhibits a decrease towards the turbulence region due to the associated velocity fluctuations, consistent with the generation of a mean entrainment velocity. The vorticity variance and  display large maxima at the T/NT interface due to the inviscid discontinuities of the tangential velocity variances existing there, and these maxima are quantitatively related to the thickness
display large maxima at the T/NT interface due to the inviscid discontinuities of the tangential velocity variances existing there, and these maxima are quantitatively related to the thickness 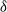 of the viscous boundary layer (VBL). For an equilibrium VBL, the RDT analysis suggests that
of the viscous boundary layer (VBL). For an equilibrium VBL, the RDT analysis suggests that 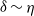 (where
(where 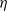 is the Kolmogorov microscale), which is consistent with the scaling law identified in a very recent DNS study for shear-free T/NT interfaces.
is the Kolmogorov microscale), which is consistent with the scaling law identified in a very recent DNS study for shear-free T/NT interfaces.
Information
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 22
- Cited by

