Published online by Cambridge University Press: 21 October 2011
We study the organization of turbulence in supersonic boundary layers through large-scale direct numerical simulations (DNS) at 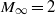 , and momentum-thickness Reynolds number up to
, and momentum-thickness Reynolds number up to 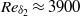 (corresponding to
(corresponding to 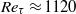 ) which significantly extend the current envelope of DNS in the supersonic regime. The numerical strategy relies on high-order, non-dissipative discretization of the convective terms in the Navier–Stokes equations, and it implements a recycling/rescaling strategy to stimulate the inflow turbulence. Comparison of the velocity statistics up to fourth order shows nearly exact agreement with reference incompressible data, provided the momentum-thickness Reynolds number is matched, and provided the mean velocity and the velocity fluctuations are scaled to incorporate the effects of mean density variation, as postulated by Morkovin’s hypothesis. As also found in the incompressible regime, we observe quite a different behaviour of the second-order flow statistics at sufficiently large Reynolds number, most of which show the onset of a range with logarithmic variation, typical of ‘attached’ variables, whereas the wall-normal velocity exhibits a plateau away from the wall, which is typical of ‘detached’ variables. The modifications of the structure of the flow field that underlie this change of behaviour are highlighted through visualizations of the velocity and temperature fields, which substantiate the formation of large jet-like and wake-like motions in the outer part of the boundary layer. It is found that the typical size of the attached eddies roughly scales with the local mean velocity gradient, rather than being proportional to the wall distance, as happens for the wall-detached variables. The interactions of the large eddies in the outer layer with the near-wall region are quantified through a two-point amplitude modulation covariance, which characterizes the modulating action of energetic outer-layer eddies.
) which significantly extend the current envelope of DNS in the supersonic regime. The numerical strategy relies on high-order, non-dissipative discretization of the convective terms in the Navier–Stokes equations, and it implements a recycling/rescaling strategy to stimulate the inflow turbulence. Comparison of the velocity statistics up to fourth order shows nearly exact agreement with reference incompressible data, provided the momentum-thickness Reynolds number is matched, and provided the mean velocity and the velocity fluctuations are scaled to incorporate the effects of mean density variation, as postulated by Morkovin’s hypothesis. As also found in the incompressible regime, we observe quite a different behaviour of the second-order flow statistics at sufficiently large Reynolds number, most of which show the onset of a range with logarithmic variation, typical of ‘attached’ variables, whereas the wall-normal velocity exhibits a plateau away from the wall, which is typical of ‘detached’ variables. The modifications of the structure of the flow field that underlie this change of behaviour are highlighted through visualizations of the velocity and temperature fields, which substantiate the formation of large jet-like and wake-like motions in the outer part of the boundary layer. It is found that the typical size of the attached eddies roughly scales with the local mean velocity gradient, rather than being proportional to the wall distance, as happens for the wall-detached variables. The interactions of the large eddies in the outer layer with the near-wall region are quantified through a two-point amplitude modulation covariance, which characterizes the modulating action of energetic outer-layer eddies.