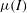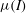1. Introduction
Steady granular chute flows, where a mass of material flowing down an inclined plane is laterally confined between two rigid vertical plates, are common in industrial set-ups and are interesting to study in their own right. The relative simplicity of the geometry also makes it an ideal test case for validating new theoretical models. An early attempt at describing these flows was carried out in GDR MiDi (Reference GDR MiDi2004), where they collated experimental data and discrete element simulations of vertical velocity profiles and basal friction curves. The two-dimensional (downslope and normal) results were used to propose a simple local rheology, where the effective-friction coefficient was a function of non-dimensional inertial number
![]() $I$
(da Cruz et al.
Reference da Cruz, Emam, Prochnow, Roux and Chevoir2005; Jop, Forterre & Pouliquen Reference Jop, Forterre and Pouliquen2005). This number is the square root of the Savage or Coulomb number (Savage Reference Savage1984; Ancey, Coussot & Evesque Reference Ancey, Coussot and Evesque1999). Jop, Forterre & Pouliquen (Reference Jop, Forterre and Pouliquen2006) generalized this scalar rheology into a full tensor constitutive law, referred to as the
$I$
(da Cruz et al.
Reference da Cruz, Emam, Prochnow, Roux and Chevoir2005; Jop, Forterre & Pouliquen Reference Jop, Forterre and Pouliquen2005). This number is the square root of the Savage or Coulomb number (Savage Reference Savage1984; Ancey, Coussot & Evesque Reference Ancey, Coussot and Evesque1999). Jop, Forterre & Pouliquen (Reference Jop, Forterre and Pouliquen2006) generalized this scalar rheology into a full tensor constitutive law, referred to as the
![]() ${\it\mu}(I)$
-rheology.
${\it\mu}(I)$
-rheology.
These governing equations allowed the chute flow configuration to be solved for the downstream velocity profile in a two-dimensional cross section (see e.g. Pouliquen et al. Reference Pouliquen, Cassar, Jop, Forterre and Nicolas2006). The full internal dynamics may also be recovered from discrete element simulations, for example Zhou & Sun (Reference Zhou and Sun2013) and Brodu, Richard & Delannay (Reference Brodu, Richard and Delannay2013). The question to be addressed is whether simpler, less computationally expensive models are able to accurately capture the full flow field for steady chute flows. Such models should account for the chute walls since these have been shown to significantly alter the flow dynamics, changing the shape and magnitude of velocity profiles (Jop et al. Reference Jop, Forterre and Pouliquen2005), as well as allowing material to flow steadily at unusually steep slope angles (Taberlet et al. Reference Taberlet, Richard, Valance, Losert, Pasini, Jenkins and Delannay2003).
Classical depth-averaged avalanche models, which do not include any higher-order viscous terms, (e.g. Gray, Tai & Noelle Reference Gray, Tai and Noelle2003) are able to accurately describe many granular flow configurations, such as a front propagating down a slope (Pouliquen Reference Pouliquen1999b
), flow over complex basal topographies (Gray, Wieland & Hutter Reference Gray, Wieland and Hutter1999) and past obstacles (Cui, Gray & Johannesson Reference Cui, Gray and Johannesson2007; Gray & Cui Reference Gray and Cui2007; Cui & Gray Reference Cui and Gray2013). However, they cannot model the velocity profile across a channel with sidewall friction, because the leading order depth-averaged downstream momentum balance does not contain any cross-slope gradients of the depth-averaged downstream velocity. As a result, the leading-order mass and momentum-balance equations admit solutions that are independent of the chute width and wall friction. Several authors (e.g. Greve & Hutter Reference Greve and Hutter1993; Taberlet et al.
Reference Taberlet, Richard, Valance, Losert, Pasini, Jenkins and Delannay2003) have attempted to address this issue by including wall-friction effects in depth- and width-averaged models, assuming Coulomb slip at the sidewalls. The resulting equations have an additional term in the effective basal friction coefficient that is proportional to the channel aspect ratio. Jop et al. (Reference Jop, Forterre and Pouliquen2005) were able to use the
![]() ${\it\mu}(I)$
-rheology to derive a width-averaged model for the velocity dependence in the vertical direction and verify several scaling laws with experimental data. Despite these successes, details of the transverse shape of the velocity profile are lost during the width-averaging process. In order to retain this information, additional physics needs to be incorporated into non-width-averaged models.
${\it\mu}(I)$
-rheology to derive a width-averaged model for the velocity dependence in the vertical direction and verify several scaling laws with experimental data. Despite these successes, details of the transverse shape of the velocity profile are lost during the width-averaging process. In order to retain this information, additional physics needs to be incorporated into non-width-averaged models.
For steady uniform flow GDR MiDi (Reference GDR MiDi2004) showed that the
![]() ${\it\mu}(I)$
-rheology was able to predict the lithostatic pressure distribution, as well as the Bagnold velocity profile that scales with the flow thickness to the power
${\it\mu}(I)$
-rheology was able to predict the lithostatic pressure distribution, as well as the Bagnold velocity profile that scales with the flow thickness to the power
![]() $3/2$
. Gray & Edwards (Reference Gray and Edwards2014) used these solutions to derive a one-dimensional depth-averaged
$3/2$
. Gray & Edwards (Reference Gray and Edwards2014) used these solutions to derive a one-dimensional depth-averaged
![]() ${\it\mu}(I)$
-rheology by including the gradient of the depth-averaged in-plane deviatoric stress in the downstream momentum-balance equation. At leading order, the depth-averaged equations reduce to those of a standard inviscid avalanche model with the
${\it\mu}(I)$
-rheology by including the gradient of the depth-averaged in-plane deviatoric stress in the downstream momentum-balance equation. At leading order, the depth-averaged equations reduce to those of a standard inviscid avalanche model with the
![]() ${\it\mu}(I)$
-rheology giving rise to an effective basal friction that is equivalent to the dynamic friction law for rough beds (Pouliquen Reference Pouliquen1999a
; Pouliquen & Forterre Reference Pouliquen and Forterre2002). An additional viscous term enters as a singular perturbation to the system and for most problems it is sufficiently small that it can be neglected. Various formulations are possible, because the leading-order relationship between the depth-averaged Bagnold velocity and the thickness allows the structure of the viscous term to be changed. The form that Gray & Edwards (Reference Gray and Edwards2014) selected is the only viscous law that does not contain singularities (in the range of angles where steady uniform flows develop) and has a coefficient of viscosity that degenerates at zero thickness. Strong evidence for this formulation is provided by the fact that it was able to match the measured cutoff frequency of roll-wave instabilities (Forterre & Pouliquen Reference Forterre and Pouliquen2003; Forterre Reference Forterre2006) without the need for any fitting parameters. In addition, Edwards & Gray (Reference Edwards and Gray2015) showed that this term plays a crucial role in the formation of steadily travelling erosion–deposition waves on erodible beds. Some caution is required, however, as the depth-averaged viscosity is negative, and the equations are ill-posed, for inclination angles outside the range where steady uniform flows are able to develop. This is a reflection of the fact that the underlying
${\it\mu}(I)$
-rheology giving rise to an effective basal friction that is equivalent to the dynamic friction law for rough beds (Pouliquen Reference Pouliquen1999a
; Pouliquen & Forterre Reference Pouliquen and Forterre2002). An additional viscous term enters as a singular perturbation to the system and for most problems it is sufficiently small that it can be neglected. Various formulations are possible, because the leading-order relationship between the depth-averaged Bagnold velocity and the thickness allows the structure of the viscous term to be changed. The form that Gray & Edwards (Reference Gray and Edwards2014) selected is the only viscous law that does not contain singularities (in the range of angles where steady uniform flows develop) and has a coefficient of viscosity that degenerates at zero thickness. Strong evidence for this formulation is provided by the fact that it was able to match the measured cutoff frequency of roll-wave instabilities (Forterre & Pouliquen Reference Forterre and Pouliquen2003; Forterre Reference Forterre2006) without the need for any fitting parameters. In addition, Edwards & Gray (Reference Edwards and Gray2015) showed that this term plays a crucial role in the formation of steadily travelling erosion–deposition waves on erodible beds. Some caution is required, however, as the depth-averaged viscosity is negative, and the equations are ill-posed, for inclination angles outside the range where steady uniform flows are able to develop. This is a reflection of the fact that the underlying
![]() ${\it\mu}(I)$
-rheology is ill-posed at high and low inertial numbers (Barker et al.
Reference Barker, Schaeffer, Bohorquez and Gray2015). The results are nevertheless sufficiently promising that this paper generalizes the depth-averaged
${\it\mu}(I)$
-rheology is ill-posed at high and low inertial numbers (Barker et al.
Reference Barker, Schaeffer, Bohorquez and Gray2015). The results are nevertheless sufficiently promising that this paper generalizes the depth-averaged
![]() ${\it\mu}(I)$
-rheology of Gray & Edwards (Reference Gray and Edwards2014) to two spatial dimensions.
${\it\mu}(I)$
-rheology of Gray & Edwards (Reference Gray and Edwards2014) to two spatial dimensions.

Figure 1. A schematic diagram of the chute inclined at a constant angle
![]() ${\it\zeta}$
to the horizontal. The coordinate system
${\it\zeta}$
to the horizontal. The coordinate system
![]() $Oxyz$
is orientated so that the
$Oxyz$
is orientated so that the
![]() $x$
-axis points down the chute, the
$x$
-axis points down the chute, the
![]() $y$
-axis points across the chute and the
$y$
-axis points across the chute and the
![]() $z$
-axis is the upward pointing normal. The granular material is constrained in the lateral direction by two parallel Perspex plates at
$z$
-axis is the upward pointing normal. The granular material is constrained in the lateral direction by two parallel Perspex plates at
![]() $y=0$
and
$y=0$
and
![]() $y=W$
. A steady uniform thickness flow rapidly develops with downstream surface velocity
$y=W$
. A steady uniform thickness flow rapidly develops with downstream surface velocity
![]() $u_{s}$
that has a cross-slope profile. In the experiments, a high-speed camera, together with particle image velocimetry (PIV) software, is used to calculate
$u_{s}$
that has a cross-slope profile. In the experiments, a high-speed camera, together with particle image velocimetry (PIV) software, is used to calculate
![]() $u_{s}(y)$
. A balance is placed at the outflow to measure the mass flux
$u_{s}(y)$
. A balance is placed at the outflow to measure the mass flux
![]() $M$
through the channel and a laser profilometer is used to record the flow thickness
$M$
through the channel and a laser profilometer is used to record the flow thickness
![]() $h$
.
$h$
.
2. Governing equations
Consider a mass of granular material flowing down a chute inclined at an angle
![]() ${\it\zeta}$
to the horizontal as shown in figure 1. Let
${\it\zeta}$
to the horizontal as shown in figure 1. Let
![]() $Oxyz$
be a Cartesian coordinate system with the
$Oxyz$
be a Cartesian coordinate system with the
![]() $x$
-axis aligned with the downslope direction, the
$x$
-axis aligned with the downslope direction, the
![]() $y$
-axis aligned with the cross-slope direction and the
$y$
-axis aligned with the cross-slope direction and the
![]() $z$
-axis normal to the chute surface. The velocity
$z$
-axis normal to the chute surface. The velocity
![]() $\boldsymbol{u}$
has components
$\boldsymbol{u}$
has components
![]() $(u,v,w)$
in the
$(u,v,w)$
in the
![]() $(x,y,z)$
directions, respectively. Assuming a rigid flat base, the free surface lies at
$(x,y,z)$
directions, respectively. Assuming a rigid flat base, the free surface lies at
![]() $z=h$
, where
$z=h$
, where
![]() $h$
is the depth of the flow. The depth-averaged velocity,
$h$
is the depth of the flow. The depth-averaged velocity,
![]() $\bar{\boldsymbol{u}}=(\bar{u},\bar{v})$
, is defined as
$\bar{\boldsymbol{u}}=(\bar{u},\bar{v})$
, is defined as
The depth-averaged mass and momentum balances, including the depth-averaged in-plane deviatoric stress gradients
![]() $\bar{{\bf\tau}}$
, are
$\bar{{\bf\tau}}$
, are
where
![]() $|\bar{\boldsymbol{u}}|=(\bar{u}^{2}+\bar{v}^{2})^{1/2}$
is the speed of the bulk flow. Gray & Edwards (Reference Gray and Edwards2014) showed that, to first order, the only effect of the
$|\bar{\boldsymbol{u}}|=(\bar{u}^{2}+\bar{v}^{2})^{1/2}$
is the speed of the bulk flow. Gray & Edwards (Reference Gray and Edwards2014) showed that, to first order, the only effect of the
![]() ${\it\mu}(I)$
-rheology is to generate an effective basal friction coefficient
${\it\mu}(I)$
-rheology is to generate an effective basal friction coefficient
![]() ${\it\mu}_{b}$
that is equivalent to the dynamic friction law measured experimentally by Pouliquen & Forterre (Reference Pouliquen and Forterre2002), i.e.
${\it\mu}_{b}$
that is equivalent to the dynamic friction law measured experimentally by Pouliquen & Forterre (Reference Pouliquen and Forterre2002), i.e.
where the Froude number
is the ratio of the magnitude of the depth-averaged speed to gravity-wave speed. The values
![]() ${\it\mu}_{1}=\tan {\it\zeta}_{1}$
and
${\it\mu}_{1}=\tan {\it\zeta}_{1}$
and
![]() ${\it\mu}_{2}=\tan {\it\zeta}_{2}$
are constants, where angles
${\it\mu}_{2}=\tan {\it\zeta}_{2}$
are constants, where angles
![]() ${\it\zeta}_{1}$
and
${\it\zeta}_{1}$
and
![]() ${\it\zeta}_{2}$
correspond to the minimum and the maximum slope angles for which steady uniform flows are observed. The length scale
${\it\zeta}_{2}$
correspond to the minimum and the maximum slope angles for which steady uniform flows are observed. The length scale
![]() $\mathscr{L}$
and dimensionless constant
$\mathscr{L}$
and dimensionless constant
![]() ${\it\beta}$
are found empirically and may depend on both the granular material and bed composition. These values have been estimated for the experimental configuration used in this paper and are summarized in table 1, together with all the other parameters which are to be held constant throughout. Note that the empirical law of Pouliquen & Forterre (Reference Pouliquen and Forterre2002) has an extended form that switches for intermediate (
${\it\beta}$
are found empirically and may depend on both the granular material and bed composition. These values have been estimated for the experimental configuration used in this paper and are summarized in table 1, together with all the other parameters which are to be held constant throughout. Note that the empirical law of Pouliquen & Forterre (Reference Pouliquen and Forterre2002) has an extended form that switches for intermediate (
![]() $0<Fr<{\it\beta}$
) and static (
$0<Fr<{\it\beta}$
) and static (
![]() $Fr=0$
) regimes. This plays an important role in the formation of erosion–deposition waves (Edwards & Gray Reference Edwards and Gray2015), but the
$Fr=0$
) regimes. This plays an important role in the formation of erosion–deposition waves (Edwards & Gray Reference Edwards and Gray2015), but the
![]() ${\it\mu}(I)$
-rheology is based on the simple law (2.5) with no switching, and so this paper will use (2.5) for all Froude numbers.
${\it\mu}(I)$
-rheology is based on the simple law (2.5) with no switching, and so this paper will use (2.5) for all Froude numbers.
Table 1. Material parameters that will remain constant throughout this paper.
2.1. The
 ${\it\mu}(I)$
-rheology and Bagnold velocity profile
${\it\mu}(I)$
-rheology and Bagnold velocity profile
The final expression on the right-hand side of the momentum equation (2.3) is the divergence of the depth-integrated deviatoric stress tensor. This term is usually very small and it is neglected in standard inviscid shallow-water-like avalanche models (see e.g. Gray et al.
Reference Gray, Tai and Noelle2003). However, in more subtle problems, such as roll waves (Forterre & Pouliquen Reference Forterre and Pouliquen2003; Forterre Reference Forterre2006; Gray & Edwards Reference Gray and Edwards2014; Razis et al.
Reference Razis, Edwards, Gray and van der Weele2014), erosion–deposition waves (Edwards & Gray Reference Edwards and Gray2015) and fingering instabilities (Pouliquen, Delour & Savage Reference Pouliquen, Delour and Savage1997; Pouliquen & Vallance Reference Pouliquen and Vallance1999; Woodhouse et al.
Reference Woodhouse, Thornton, Johnson, Kokelaar and Gray2012) it plays a critical role in obtaining the correct solution. The depth-averaged deviatoric stress tensor
![]() $\bar{{\bf\tau}}$
is defined by
$\bar{{\bf\tau}}$
is defined by
where
![]() ${\bf\tau}$
is the deviatoric component of the (three-dimensional) Cauchy stress tensor
${\bf\tau}$
is the deviatoric component of the (three-dimensional) Cauchy stress tensor
![]() $p$
is the pressure and
$p$
is the pressure and
![]() $\unicode[STIX]{x1D644}$
is the
$\unicode[STIX]{x1D644}$
is the
![]() $3\times 3$
identity matrix. The specific form of the deviatoric tensor comes from the
$3\times 3$
identity matrix. The specific form of the deviatoric tensor comes from the
![]() ${\it\mu}(I)$
-rheology for dense granular flows (GDR MiDi Reference GDR MiDi2004; Jop et al.
Reference Jop, Forterre and Pouliquen2005, Reference Jop, Forterre and Pouliquen2006). It is a pressure and strain-rate dependent law of the form
${\it\mu}(I)$
-rheology for dense granular flows (GDR MiDi Reference GDR MiDi2004; Jop et al.
Reference Jop, Forterre and Pouliquen2005, Reference Jop, Forterre and Pouliquen2006). It is a pressure and strain-rate dependent law of the form
where the strain rate,
![]() $\unicode[STIX]{x1D63F}$
, is defined as
$\unicode[STIX]{x1D63F}$
, is defined as
the velocity gradient
![]() $\unicode[STIX]{x1D647}=\text{grad}\,\boldsymbol{u}$
, and the superscript T is the transpose. The second invariant of the strain-rate tensor is
$\unicode[STIX]{x1D647}=\text{grad}\,\boldsymbol{u}$
, and the superscript T is the transpose. The second invariant of the strain-rate tensor is
The definitions (2.10) and (2.11) are equivalent to those used in Jop et al. (Reference Jop, Forterre and Pouliquen2006), with the factors of two arising from the standard choice of the strain-rate tensor. The non-dimensional inertial number
![]() $I$
is then
$I$
is then
where
![]() $d$
is the particle diameter and
$d$
is the particle diameter and
![]() ${\it\rho}^{\ast }$
is the intrinsic solid density of the grains. The function
${\it\rho}^{\ast }$
is the intrinsic solid density of the grains. The function
![]() ${\it\mu}(I)$
is derived from the basal friction law (2.5) (Jop et al.
Reference Jop, Forterre and Pouliquen2005; Gray & Edwards Reference Gray and Edwards2014) and takes the form
${\it\mu}(I)$
is derived from the basal friction law (2.5) (Jop et al.
Reference Jop, Forterre and Pouliquen2005; Gray & Edwards Reference Gray and Edwards2014) and takes the form
where the constant
![]() $I_{0}$
is given by
$I_{0}$
is given by
and
![]() ${\it\Phi}$
is the solids volume fraction.
${\it\Phi}$
is the solids volume fraction.
In one spatial dimension, the constitutive law (2.8)–(2.14) may be solved for steady uniform flows (e.g. GDR MiDi Reference GDR MiDi2004; Gray & Edwards Reference Gray and Edwards2014). In this configuration, mass balance is trivially satisfied since
![]() $v$
and
$v$
and
![]() $w$
are identically zero and the downslope velocity
$w$
are identically zero and the downslope velocity
![]() $u$
depends on
$u$
depends on
![]() $z$
only, so that
$z$
only, so that
![]() $\Vert \unicode[STIX]{x1D63F}\Vert =|\partial u/\partial z|/2$
. The normal component of the momentum balance implies that the pressure is lithostatic, i.e.
$\Vert \unicode[STIX]{x1D63F}\Vert =|\partial u/\partial z|/2$
. The normal component of the momentum balance implies that the pressure is lithostatic, i.e.
where
![]() ${\it\rho}={\it\rho}^{\ast }{\it\Phi}$
is the density of the flow. The downslope momentum balance can also be integrated to show that the shear stress is
${\it\rho}={\it\rho}^{\ast }{\it\Phi}$
is the density of the flow. The downslope momentum balance can also be integrated to show that the shear stress is
Substituting (2.15) and (2.16) into the
![]() $xz$
component of the
$xz$
component of the
![]() ${\it\mu}(I)$
-rheology (2.9) implies that
${\it\mu}(I)$
-rheology (2.9) implies that
![]() ${\it\mu}(I)=\tan {\it\zeta}$
, provided
${\it\mu}(I)=\tan {\it\zeta}$
, provided
![]() $\partial u/\partial z$
is positive. Hence for a fixed slope angle the inertial number
$\partial u/\partial z$
is positive. Hence for a fixed slope angle the inertial number
![]() $I$
is equal to a constant
$I$
is equal to a constant
![]() $I_{{\it\zeta}}$
, where
$I_{{\it\zeta}}$
, where
Since
![]() $I$
is constant, (2.12) can be solved for the downslope velocity
$I$
is constant, (2.12) can be solved for the downslope velocity
This is known as the Bagnold velocity profile. Integrating (2.18) through the avalanche depth implies that the depth-averaged Bagnold velocity is
2.2. The one-dimensional depth-averaged
 ${\it\mu}(I)$
-rheology
${\it\mu}(I)$
-rheology
It is useful to briefly summarize how Gray & Edwards (Reference Gray and Edwards2014) derived their depth-averaged viscous term in one-spatial dimension. The
![]() ${\it\mu}(I)$
-rheology implies that the downslope in-plane deviatoric stress is
${\it\mu}(I)$
-rheology implies that the downslope in-plane deviatoric stress is
Using the shallowness of the avalanche, the in-plane strain rate was approximated by differentiating the Bagnold velocity profile (2.18) with respect to
![]() $x$
, assuming that the thickness
$x$
, assuming that the thickness
![]() $h$
was now a slowly varying function of
$h$
was now a slowly varying function of
![]() $x$
, i.e. that
$x$
, i.e. that
Similarly, to leading order, the second invariant of the strain-rate tensor could also be evaluated using the Bagnold velocity profile, i.e.
Substituting (2.15), (2.21) and (2.22) into (2.20) and using
![]() ${\it\mu}(I_{{\it\zeta}})=\tan {\it\zeta}$
implies that
${\it\mu}(I_{{\it\zeta}})=\tan {\it\zeta}$
implies that
Integrating this through the avalanche depth it follows that a leading-order approximation for the depth-averaged deviatoric in plane stress is
A variety of depth-averaged models are possible at this order, because the relationship between the depth-averaged Bagnold velocity and the thickness (2.19) can be used to reformulate (2.24) into a more conventional depth-averaged viscous law. For instance, from (2.19) it follows that the thickness gradient is
and then (2.24) becomes
where the definitions of
![]() $I_{0}$
and
$I_{0}$
and
![]() $I_{{\it\zeta}}$
, (2.14) and (2.17), imply that the coefficient
$I_{{\it\zeta}}$
, (2.14) and (2.17), imply that the coefficient
![]() ${\it\nu}$
in the depth-averaged viscosity can be expressed as
${\it\nu}$
in the depth-averaged viscosity can be expressed as
Note that the density
![]() ${\it\rho}$
in (2.26) cancels out in the momentum balance (2.3) to produce a viscous term with a second-order gradient of the depth-averaged velocity. This particular formulation is the only one in the current framework which introduces such gradients without also introducing singularities in
${\it\rho}$
in (2.26) cancels out in the momentum balance (2.3) to produce a viscous term with a second-order gradient of the depth-averaged velocity. This particular formulation is the only one in the current framework which introduces such gradients without also introducing singularities in
![]() $h$
or
$h$
or
![]() $\bar{u}$
for inclination angles in the range of steady uniform flow, i.e.
$\bar{u}$
for inclination angles in the range of steady uniform flow, i.e.
![]() ${\it\zeta}\in ({\it\zeta}_{1},{\it\zeta}_{2})$
. It has a coefficient of viscosity
${\it\zeta}\in ({\it\zeta}_{1},{\it\zeta}_{2})$
. It has a coefficient of viscosity
![]() ${\it\nu}h^{3/2}/2$
that automatically degenerates when the avalanche thickness equals zero, which is another desirable property of depth-averaged viscous laws. Gray & Edwards (Reference Gray and Edwards2014) showed that this formulation did not change the shape of a granular front as it propagates down a rough inclined plane (Pouliquen Reference Pouliquen1999b
) and that it was able to match the experimental cutoff frequency of roll waves (Forterre & Pouliquen Reference Forterre and Pouliquen2003; Forterre Reference Forterre2006) without the need for any fitting parameters. This is a strong indication that the decreasing viscosity with increasing inclination angle in (2.27) is correct, at least in the range of steady uniform flow. Edwards & Gray (Reference Edwards and Gray2015) have shown that this term also plays a crucial role in the formation of steadily travelling erosion–deposition waves on erodible beds, which have regions of completely stationary grains. It should be noted, however, that outside the regime in which steady uniform flow is possible the coefficient
${\it\nu}h^{3/2}/2$
that automatically degenerates when the avalanche thickness equals zero, which is another desirable property of depth-averaged viscous laws. Gray & Edwards (Reference Gray and Edwards2014) showed that this formulation did not change the shape of a granular front as it propagates down a rough inclined plane (Pouliquen Reference Pouliquen1999b
) and that it was able to match the experimental cutoff frequency of roll waves (Forterre & Pouliquen Reference Forterre and Pouliquen2003; Forterre Reference Forterre2006) without the need for any fitting parameters. This is a strong indication that the decreasing viscosity with increasing inclination angle in (2.27) is correct, at least in the range of steady uniform flow. Edwards & Gray (Reference Edwards and Gray2015) have shown that this term also plays a crucial role in the formation of steadily travelling erosion–deposition waves on erodible beds, which have regions of completely stationary grains. It should be noted, however, that outside the regime in which steady uniform flow is possible the coefficient
![]() ${\it\nu}$
is negative and the theory is ill-posed. This is a signature of the ill-posedness of the full
${\it\nu}$
is negative and the theory is ill-posed. This is a signature of the ill-posedness of the full
![]() ${\it\mu}(I)$
-rheology at high and low inertial numbers (Barker et al.
Reference Barker, Schaeffer, Bohorquez and Gray2015). For flows outside the range where steady uniform flows develop (i.e.
${\it\mu}(I)$
-rheology at high and low inertial numbers (Barker et al.
Reference Barker, Schaeffer, Bohorquez and Gray2015). For flows outside the range where steady uniform flows develop (i.e.
![]() ${\it\zeta}\notin ({\it\zeta}_{1},{\it\zeta}_{2})$
), some form of regularization must be applied to ensure the depth-averaged system remains well-posed.
${\it\zeta}\notin ({\it\zeta}_{1},{\it\zeta}_{2})$
), some form of regularization must be applied to ensure the depth-averaged system remains well-posed.
3. Generalization to tensor form
The success of the depth-averaged
![]() ${\it\mu}(I)$
-rheology of Gray & Edwards (Reference Gray and Edwards2014) in modelling one-dimensional problems suggests using a similar formulation for two dimensions. Motivated by (2.26), the expression
${\it\mu}(I)$
-rheology of Gray & Edwards (Reference Gray and Edwards2014) in modelling one-dimensional problems suggests using a similar formulation for two dimensions. Motivated by (2.26), the expression
is chosen as the generalization to a two-dimensional tensor relation, where
is the depth-integrated strain-rate tensor and
![]() $\bar{\unicode[STIX]{x1D647}}=\boldsymbol{{\rm\nabla}}\bar{\boldsymbol{u}}$
is the two-dimensional gradient of the depth-averaged velocity. This constitutive law is both consistent with the one-dimensional depth-averaged
$\bar{\unicode[STIX]{x1D647}}=\boldsymbol{{\rm\nabla}}\bar{\boldsymbol{u}}$
is the two-dimensional gradient of the depth-averaged velocity. This constitutive law is both consistent with the one-dimensional depth-averaged
![]() ${\it\mu}(I)$
-rheology of Gray & Edwards (Reference Gray and Edwards2014) and satisfies the principle of material frame indifference or objectivity. This states that the response of the material must be the same for any pair of equivalent observers, i.e. the constitutive law must be invariant under changes of frame that preserve the structure of space and time. Usually, this principle is formulated in a full three-dimensional context (e.g. Chadwick Reference Chadwick1976), but in the depth-averaged framework it should be restricted to the downslope and lateral directions (relative to the static bed). The rigid base may cause a degree of anisotropy in the normal direction, but the effective horizontal viscosity should not have a favoured reference orientation. Chadwick (Reference Chadwick1976, p. 136) gives a necessary and sufficient condition for a viscous law to be invariant under change of frame in three dimensions. The same principle can be applied in the depth-averaged case by assuming that the depth-averaged deviatoric stress is given by a symmetric tensor-valued function
${\it\mu}(I)$
-rheology of Gray & Edwards (Reference Gray and Edwards2014) and satisfies the principle of material frame indifference or objectivity. This states that the response of the material must be the same for any pair of equivalent observers, i.e. the constitutive law must be invariant under changes of frame that preserve the structure of space and time. Usually, this principle is formulated in a full three-dimensional context (e.g. Chadwick Reference Chadwick1976), but in the depth-averaged framework it should be restricted to the downslope and lateral directions (relative to the static bed). The rigid base may cause a degree of anisotropy in the normal direction, but the effective horizontal viscosity should not have a favoured reference orientation. Chadwick (Reference Chadwick1976, p. 136) gives a necessary and sufficient condition for a viscous law to be invariant under change of frame in three dimensions. The same principle can be applied in the depth-averaged case by assuming that the depth-averaged deviatoric stress is given by a symmetric tensor-valued function
![]() $\unicode[STIX]{x1D641}=\unicode[STIX]{x1D641}(\bar{\unicode[STIX]{x1D647}})$
of the depth-averaged velocity gradient. The constitutive law (3.1) can then be written as
$\unicode[STIX]{x1D641}=\unicode[STIX]{x1D641}(\bar{\unicode[STIX]{x1D647}})$
of the depth-averaged velocity gradient. The constitutive law (3.1) can then be written as
and the principle of objectivity requires that
for all proper orthogonal tensors
![]() $\unicode[STIX]{x1D64C}$
and all skew-symmetric tensors
$\unicode[STIX]{x1D64C}$
and all skew-symmetric tensors
![]() ${\it\bf\Omega}$
. This is easily checked by direct substitution, i.e.
${\it\bf\Omega}$
. This is easily checked by direct substitution, i.e.
Using the fact that
![]() ${\it\bf\Omega}=-{\it\bf\Omega}^{\text{T}}$
, it follows that the right-hand side reduces to
${\it\bf\Omega}=-{\it\bf\Omega}^{\text{T}}$
, it follows that the right-hand side reduces to
which confirms that the constitutive law (3.1) satisfies the principle of objectivity (3.4) in two dimensions.
Note that when the two-dimensional constitutive law (3.1) is substituted into the momentum balance (2.3), the density
![]() ${\it\rho}$
cancels out. The complete system of depth-averaged mass and momentum equations (2.2), (2.3) in component form is then
${\it\rho}$
cancels out. The complete system of depth-averaged mass and momentum equations (2.2), (2.3) in component form is then
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\partial }{\partial t}(h\bar{u})+\frac{\partial }{\partial x}(h\bar{u}^{2})+\frac{\partial }{\partial y}(h\bar{u}\bar{v})+\frac{\partial }{\partial x}\left(\frac{1}{2}gh^{2}\cos {\it\zeta}\right)=ghS_{x}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{\partial }{\partial x}\left({\it\nu}h^{3/2}\frac{\partial \bar{u}}{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{1}{2}{\it\nu}h^{3/2}\left(\frac{\partial \bar{u}}{\partial y}+\frac{\partial \bar{v}}{\partial x}\right)\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\partial }{\partial t}(h\bar{u})+\frac{\partial }{\partial x}(h\bar{u}^{2})+\frac{\partial }{\partial y}(h\bar{u}\bar{v})+\frac{\partial }{\partial x}\left(\frac{1}{2}gh^{2}\cos {\it\zeta}\right)=ghS_{x}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{\partial }{\partial x}\left({\it\nu}h^{3/2}\frac{\partial \bar{u}}{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{1}{2}{\it\nu}h^{3/2}\left(\frac{\partial \bar{u}}{\partial y}+\frac{\partial \bar{v}}{\partial x}\right)\right),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\partial }{\partial t}(h\bar{v})+\frac{\partial }{\partial x}(h\bar{u}\bar{v})+\frac{\partial }{\partial y}(h\bar{v}^{2})+\frac{\partial }{\partial y}\left(\frac{1}{2}gh^{2}\cos {\it\zeta}\right)=ghS_{y}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{\partial }{\partial x}\left(\frac{1}{2}{\it\nu}h^{3/2}\left(\frac{\partial \bar{u}}{\partial y}+\frac{\partial \bar{v}}{\partial x}\right)\right)+\frac{\partial }{\partial y}\left({\it\nu}h^{3/2}\frac{\partial \bar{v}}{\partial y}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\partial }{\partial t}(h\bar{v})+\frac{\partial }{\partial x}(h\bar{u}\bar{v})+\frac{\partial }{\partial y}(h\bar{v}^{2})+\frac{\partial }{\partial y}\left(\frac{1}{2}gh^{2}\cos {\it\zeta}\right)=ghS_{y}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{\partial }{\partial x}\left(\frac{1}{2}{\it\nu}h^{3/2}\left(\frac{\partial \bar{u}}{\partial y}+\frac{\partial \bar{v}}{\partial x}\right)\right)+\frac{\partial }{\partial y}\left({\it\nu}h^{3/2}\frac{\partial \bar{v}}{\partial y}\right),\end{eqnarray}$$
4. Steady fully-developed flows between parallel plates
Consider the set-up of figure 1, where a granular material flows over a rough base inclined at a constant angle
![]() ${\it\zeta}$
to the horizontal and is confined in the lateral direction by two parallel plates at
${\it\zeta}$
to the horizontal and is confined in the lateral direction by two parallel plates at
![]() $y=0$
and
$y=0$
and
![]() $y=W$
. Upon seeking steady uniform solutions, independent of time
$y=W$
. Upon seeking steady uniform solutions, independent of time
![]() $t$
and downslope position
$t$
and downslope position
![]() $x$
, conservation of mass (3.7) reduces to
$x$
, conservation of mass (3.7) reduces to
Integrating, and using the fact that
![]() $\bar{v}=0$
at the rigid lateral boundaries, ensures
$\bar{v}=0$
at the rigid lateral boundaries, ensures
![]() $h\bar{v}$
is equal to zero everywhere. For non-trivial solutions it follows that
$h\bar{v}$
is equal to zero everywhere. For non-trivial solutions it follows that
throughout the flow. The
![]() $y$
component of the momentum equation (3.9) then reduces to
$y$
component of the momentum equation (3.9) then reduces to
which implies that the thickness is equal to a constant,
Experimental measurements (e.g. Jop et al.
Reference Jop, Forterre and Pouliquen2005) show a maximum in the thickness profile down the centre of the channel, but the variations are small in magnitude (Brodu et al.
Reference Brodu, Richard and Delannay2013). Similarly, the measured transverse velocities are negligible (
![]() ${<}$
1 % of the downslope magnitudes according to Jop et al.
Reference Jop, Forterre and Pouliquen2005) and so the statements (4.2) and (4.4) are plausible as leading-order approximations. With these assumptions, (3.8) reduces to a second-order ODE for the depth-averaged velocity
${<}$
1 % of the downslope magnitudes according to Jop et al.
Reference Jop, Forterre and Pouliquen2005) and so the statements (4.2) and (4.4) are plausible as leading-order approximations. With these assumptions, (3.8) reduces to a second-order ODE for the depth-averaged velocity
![]() $\bar{u}(y)$
,
$\bar{u}(y)$
,
where
![]() $\text{sgn}$
is the sign function and ensures the friction always opposes the direction of motion. The basal friction coefficient (2.5) is now written in terms of the downslope velocity as
$\text{sgn}$
is the sign function and ensures the friction always opposes the direction of motion. The basal friction coefficient (2.5) is now written in terms of the downslope velocity as
where the constant
is positive for the same range of slope angles for which the depth-averaged theory is well-posed. The steady uniform depth-averaged downstream velocity
![]() $\bar{u}_{0}$
satisfies
$\bar{u}_{0}$
satisfies
![]() ${\it\mu}_{b}(\bar{u}_{0})=\tan {\it\zeta}$
and is given by
${\it\mu}_{b}(\bar{u}_{0})=\tan {\it\zeta}$
and is given by
Note that (2.14) and (2.17) imply that this is equivalent to the depth-averaged Bagnold profile (2.19) with constant flow thickness
![]() $h=h_{0}$
. This paper will consider two different boundary conditions at the sidewalls to accompany equation (4.5). The first is a no-slip condition,
$h=h_{0}$
. This paper will consider two different boundary conditions at the sidewalls to accompany equation (4.5). The first is a no-slip condition,
which is appropriate for walls made of the same material as the bulk flow (Jop et al.
Reference Jop, Forterre and Pouliquen2006). If the plates are sufficiently smooth, it is expected that there will be a slip velocity at each boundary, inducing a stress in the material. Following Taberlet et al. (Reference Taberlet, Richard, Valance, Losert, Pasini, Jenkins and Delannay2003), the depth-integrated stress at each wall is assumed to be proportional to the depth-integrated pressure. Denoting this deviatoric stress by
![]() $h\bar{{\it\tau}}_{w}$
and assuming a lithostatic pressure distribution leads to
$h\bar{{\it\tau}}_{w}$
and assuming a lithostatic pressure distribution leads to
which may be evaluated explicitly to give
where
![]() $\bar{u}_{w}=\bar{u}(0)=\bar{u}(W)$
denotes the slip velocity at the walls. Since the basal friction coefficient (4.6) is velocity dependent, in general one might anticipate a similar relation for the wall friction coefficient
$\bar{u}_{w}=\bar{u}(0)=\bar{u}(W)$
denotes the slip velocity at the walls. Since the basal friction coefficient (4.6) is velocity dependent, in general one might anticipate a similar relation for the wall friction coefficient
![]() ${\it\mu}_{w}$
. Here, Coulomb slip is assumed for simplicity, with constant
${\it\mu}_{w}$
. Here, Coulomb slip is assumed for simplicity, with constant
![]() ${\it\mu}_{w}=\tan {\it\zeta}_{w}$
. The effect of changing the value of
${\it\mu}_{w}=\tan {\it\zeta}_{w}$
. The effect of changing the value of
![]() ${\it\zeta}_{w}$
will be discussed later in this paper.
${\it\zeta}_{w}$
will be discussed later in this paper.
Taking
![]() $(\boldsymbol{i},\boldsymbol{j})$
to be the standard unit vectors in the
$(\boldsymbol{i},\boldsymbol{j})$
to be the standard unit vectors in the
![]() $(x,y)$
plane, the wall stress can also be written in terms of the depth-integrated stress tensor
$(x,y)$
plane, the wall stress can also be written in terms of the depth-integrated stress tensor
![]() $h\bar{{\bf\tau}}$
, given by (3.1) and (3.2), as
$h\bar{{\bf\tau}}$
, given by (3.1) and (3.2), as
where
![]() $\boldsymbol{n}$
is the outward facing normal. Substituting explicitly for the stress tensor and using the fact that
$\boldsymbol{n}$
is the outward facing normal. Substituting explicitly for the stress tensor and using the fact that
![]() $\boldsymbol{n}=-\boldsymbol{j}$
at
$\boldsymbol{n}=-\boldsymbol{j}$
at
![]() $y=0$
and
$y=0$
and
![]() $\boldsymbol{n}=\boldsymbol{j}$
at
$\boldsymbol{n}=\boldsymbol{j}$
at
![]() $y=W$
leads to
$y=W$
leads to
 $$\begin{eqnarray}h\bar{{\it\tau}}_{w}=\left\{\begin{array}{@{}ll@{}}\displaystyle -\frac{1}{2}{\it\rho}{\it\nu}h^{3/2}\left(\frac{\partial \bar{u}}{\partial y}+\frac{\partial \bar{v}}{\partial x}\right)\quad & \text{at}~y=0,\\ \displaystyle \frac{1}{2}{\it\rho}{\it\nu}h^{3/2}\left(\frac{\partial \bar{u}}{\partial y}+\frac{\partial \bar{v}}{\partial x}\right)\quad & \text{at}~y=W.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}h\bar{{\it\tau}}_{w}=\left\{\begin{array}{@{}ll@{}}\displaystyle -\frac{1}{2}{\it\rho}{\it\nu}h^{3/2}\left(\frac{\partial \bar{u}}{\partial y}+\frac{\partial \bar{v}}{\partial x}\right)\quad & \text{at}~y=0,\\ \displaystyle \frac{1}{2}{\it\rho}{\it\nu}h^{3/2}\left(\frac{\partial \bar{u}}{\partial y}+\frac{\partial \bar{v}}{\partial x}\right)\quad & \text{at}~y=W.\end{array}\right.\end{eqnarray}$$
Finally, equating the two expressions (4.11) and (4.13), and using
![]() $\bar{v}\equiv 0$
and constant flow thickness
$\bar{v}\equiv 0$
and constant flow thickness
![]() $h=h_{0}$
for steady uniform chute flows, gives an alternative set of boundary conditions where the velocity gradients are specified at the sidewalls,
$h=h_{0}$
for steady uniform chute flows, gives an alternative set of boundary conditions where the velocity gradients are specified at the sidewalls,
4.1. Non-dimensionalisation
The steady uniform velocity
![]() $\bar{u}_{0}$
and channel width
$\bar{u}_{0}$
and channel width
![]() $W$
provide convenient length scales to non-dimensionalise the problem by introducing the scalings
$W$
provide convenient length scales to non-dimensionalise the problem by introducing the scalings
where the hats denote dimensionless quantities. Substituting into the ODE (4.5) and using the expressions (2.27), (4.7) and (4.8) for simplification gives
where the channel aspect ratio is defined as
![]() ${\it\varepsilon}=h_{0}/W$
. The basal friction law is written in terms of non-dimensional variables as
${\it\varepsilon}=h_{0}/W$
. The basal friction law is written in terms of non-dimensional variables as
In view of the scalings (4.16), the no-slip boundary conditions (4.9) become
and the alternative slip boundary conditions (4.14) and (4.15) reduce to

Figure 2. Depth-averaged velocity profiles
![]() $\hat{\bar{u}}({\hat{y}})$
for different channel aspect ratios
$\hat{\bar{u}}({\hat{y}})$
for different channel aspect ratios
![]() ${\it\varepsilon}$
. The curves are obtained by solving (4.17) subject to no-slip boundary conditions (4.19) for a fixed slope angle
${\it\varepsilon}$
. The curves are obtained by solving (4.17) subject to no-slip boundary conditions (4.19) for a fixed slope angle
![]() ${\it\zeta}=26^{\circ }$
. The dashed line denotes the solution to the inviscid equations
${\it\zeta}=26^{\circ }$
. The dashed line denotes the solution to the inviscid equations
![]() $\hat{\bar{u}}({\hat{y}})=1$
.
$\hat{\bar{u}}({\hat{y}})=1$
.
Figures 2 and 3 show example numerical solutions of (4.17) that have been computed with bvp5c in Matlab. Figure 2 shows how the non-dimensional velocity profile changes as a function of the channel aspect ratio
![]() ${\it\varepsilon}$
for fixed inclination and frictional properties and no-slip conditions at the walls (4.19). For small values of
${\it\varepsilon}$
for fixed inclination and frictional properties and no-slip conditions at the walls (4.19). For small values of
![]() ${\it\varepsilon}$
, corresponding to wide, shallow channels, the sidewalls have less effect on the overall flow. In this case, the velocity is dominated by the constant
${\it\varepsilon}$
, corresponding to wide, shallow channels, the sidewalls have less effect on the overall flow. In this case, the velocity is dominated by the constant
![]() $\hat{\bar{u}}({\hat{y}})=1$
, or
$\hat{\bar{u}}({\hat{y}})=1$
, or
![]() $\bar{u}(y)=\bar{u}_{0}$
in dimensional variables, which is the solution to the inviscid equations (
$\bar{u}(y)=\bar{u}_{0}$
in dimensional variables, which is the solution to the inviscid equations (
![]() ${\it\nu}=0$
). However, these constant profiles do not satisfy the no-slip boundary conditions, meaning that boundary layers form at the walls. A simple asymptotic analysis of the governing ODE (4.17) as
${\it\nu}=0$
). However, these constant profiles do not satisfy the no-slip boundary conditions, meaning that boundary layers form at the walls. A simple asymptotic analysis of the governing ODE (4.17) as
![]() ${\it\varepsilon}\longrightarrow 0$
reveals that the width of these boundary layers scales with
${\it\varepsilon}\longrightarrow 0$
reveals that the width of these boundary layers scales with
![]() ${\it\varepsilon}$
. As the aspect ratio increases, so that
${\it\varepsilon}$
. As the aspect ratio increases, so that
![]() ${\it\varepsilon}$
may no longer be considered a small parameter, the lateral walls have an effect everywhere in the channel, rather than localized at the boundaries. For these narrower flows, the profiles then resemble parabolas with approximately constant curvature across the chute width. The maximum centreline velocities decrease with increasing
${\it\varepsilon}$
may no longer be considered a small parameter, the lateral walls have an effect everywhere in the channel, rather than localized at the boundaries. For these narrower flows, the profiles then resemble parabolas with approximately constant curvature across the chute width. The maximum centreline velocities decrease with increasing
![]() ${\it\varepsilon}$
. Indeed, in the limit of very large aspect ratios, the leading-order behaviour of (4.17) subject to (4.19) is
${\it\varepsilon}$
. Indeed, in the limit of very large aspect ratios, the leading-order behaviour of (4.17) subject to (4.19) is
as
![]() ${\it\varepsilon}\longrightarrow \infty$
, confirming the parabolic shape. However, such large values of
${\it\varepsilon}\longrightarrow \infty$
, confirming the parabolic shape. However, such large values of
![]() ${\it\varepsilon}$
correspond to much narrower channels than are typically seen in physical systems, and also violate the shallowness assumption required for depth-averaged models, and so (4.22) is of limited practical use.
${\it\varepsilon}$
correspond to much narrower channels than are typically seen in physical systems, and also violate the shallowness assumption required for depth-averaged models, and so (4.22) is of limited practical use.

Figure 3. Main plot: solutions of the second-order ODE (4.17) subject to slip boundary conditions (4.20) and (4.21). The slope angle and aspect ratio are fixed at
![]() ${\it\zeta}=26^{\circ }$
and
${\it\zeta}=26^{\circ }$
and
![]() ${\it\varepsilon}=0.1$
, respectively, and the wall-friction angle
${\it\varepsilon}=0.1$
, respectively, and the wall-friction angle
![]() ${\it\zeta}_{w}$
is varied. The dashed line denotes the solution to the inviscid equations
${\it\zeta}_{w}$
is varied. The dashed line denotes the solution to the inviscid equations
![]() $\hat{\bar{u}}({\hat{y}})=1$
, corresponding to the limit of no wall friction
$\hat{\bar{u}}({\hat{y}})=1$
, corresponding to the limit of no wall friction
![]() ${\it\zeta}_{w}\longrightarrow 0$
. Inset: slip velocity
${\it\zeta}_{w}\longrightarrow 0$
. Inset: slip velocity
![]() $\hat{\bar{u}}_{w}=\hat{\bar{u}}(0)=\hat{\bar{u}}(1)$
as a function of wall-friction angle
$\hat{\bar{u}}_{w}=\hat{\bar{u}}(0)=\hat{\bar{u}}(1)$
as a function of wall-friction angle
![]() ${\it\zeta}_{w}$
. Beyond a critical angle
${\it\zeta}_{w}$
. Beyond a critical angle
![]() ${\it\zeta}_{w}={\it\zeta}_{w}^{\ast }$
the sign of the velocity is explicitly included in the ODE (4.17) and boundary conditions (4.20), (4.21), which generates a solution that is equivalent to no slip (4.19) at the sidewalls.
${\it\zeta}_{w}={\it\zeta}_{w}^{\ast }$
the sign of the velocity is explicitly included in the ODE (4.17) and boundary conditions (4.20), (4.21), which generates a solution that is equivalent to no slip (4.19) at the sidewalls.
The alternative slip boundary conditions are explored in figure 3, where (4.17) is solved subject to (4.20) and (4.21) for different wall-friction angles
![]() ${\it\zeta}_{w}$
(the aspect ratio and slope angle remain fixed in this case). In the limiting case
${\it\zeta}_{w}$
(the aspect ratio and slope angle remain fixed in this case). In the limiting case
![]() ${\it\zeta}_{w}=0$
of no wall friction, the velocity profiles are given by the constant
${\it\zeta}_{w}=0$
of no wall friction, the velocity profiles are given by the constant
![]() $\hat{\bar{u}}({\hat{y}})=1$
, corresponding to steady uniform solutions of the inviscid equations. As
$\hat{\bar{u}}({\hat{y}})=1$
, corresponding to steady uniform solutions of the inviscid equations. As
![]() ${\it\zeta}_{w}$
increases, the maximum velocity in the centre of the channel remains similar, but the slip velocity at the walls decreases, leading to more curved profiles. There is a critical amount of wall friction
${\it\zeta}_{w}$
increases, the maximum velocity in the centre of the channel remains similar, but the slip velocity at the walls decreases, leading to more curved profiles. There is a critical amount of wall friction
![]() ${\it\zeta}_{w}={\it\zeta}_{w}^{\ast }$
where this slip velocity first reaches zero. Beyond this point, one might anticipate negative velocities to be generated, but the ODE (4.17) and boundary conditions (4.20), (4.21) combine to automatically pin the wall velocity to zero, i.e. they select no-slip conditions at the walls (see inset of figure 3). This is surprising as we do not explicitly impose this. To see the reason for this, note that
${\it\zeta}_{w}={\it\zeta}_{w}^{\ast }$
where this slip velocity first reaches zero. Beyond this point, one might anticipate negative velocities to be generated, but the ODE (4.17) and boundary conditions (4.20), (4.21) combine to automatically pin the wall velocity to zero, i.e. they select no-slip conditions at the walls (see inset of figure 3). This is surprising as we do not explicitly impose this. To see the reason for this, note that
![]() ${\it\mu}_{b}(\hat{\bar{u}})\leqslant \tan {\it\zeta}$
for
${\it\mu}_{b}(\hat{\bar{u}})\leqslant \tan {\it\zeta}$
for
![]() $|\hat{\bar{u}}|\leqslant 1$
, so the right-hand side of (4.17) is negative irrespective of the sign of
$|\hat{\bar{u}}|\leqslant 1$
, so the right-hand side of (4.17) is negative irrespective of the sign of
![]() $\hat{\bar{u}}$
. Solutions to the ODE (4.17) therefore have the property that the velocity profiles are concave, i.e.
$\hat{\bar{u}}$
. Solutions to the ODE (4.17) therefore have the property that the velocity profiles are concave, i.e.
![]() $\text{d}^{2}\hat{\bar{u}}/\text{d}{\hat{y}}^{2}\leqslant 0$
. However, negative wall velocities would cause the sign functions in the boundary conditions (4.20), (4.21) to flip from positive to negative, and the velocity profiles would then necessarily have some regions of convexity, which is not allowed. With the combination of sign functions and modulus signs the solver therefore automatically selects whether a no slip (4.19) or slip (4.20), (4.21) boundary condition is applied. Consequently, for a given aspect ratio and slope angle, there will be a slip velocity if
$\text{d}^{2}\hat{\bar{u}}/\text{d}{\hat{y}}^{2}\leqslant 0$
. However, negative wall velocities would cause the sign functions in the boundary conditions (4.20), (4.21) to flip from positive to negative, and the velocity profiles would then necessarily have some regions of convexity, which is not allowed. With the combination of sign functions and modulus signs the solver therefore automatically selects whether a no slip (4.19) or slip (4.20), (4.21) boundary condition is applied. Consequently, for a given aspect ratio and slope angle, there will be a slip velocity if
![]() ${\it\zeta}_{w}<{\it\zeta}_{w}^{\ast }$
and no slip if
${\it\zeta}_{w}<{\it\zeta}_{w}^{\ast }$
and no slip if
![]() ${\it\zeta}_{w}\geqslant {\it\zeta}_{w}^{\ast }$
. The corresponding phase diagrams for different values of
${\it\zeta}_{w}\geqslant {\it\zeta}_{w}^{\ast }$
. The corresponding phase diagrams for different values of
![]() ${\it\varepsilon}$
and
${\it\varepsilon}$
and
![]() ${\it\zeta}_{1}<{\it\zeta}<{\it\zeta}_{2}$
are shown in figure 4, with the lines where
${\it\zeta}_{1}<{\it\zeta}<{\it\zeta}_{2}$
are shown in figure 4, with the lines where
![]() ${\it\zeta}_{w}={\it\zeta}_{w}^{\ast }$
marking the transition between the two regimes. There is only a very weak dependence of
${\it\zeta}_{w}={\it\zeta}_{w}^{\ast }$
marking the transition between the two regimes. There is only a very weak dependence of
![]() ${\it\zeta}_{w}^{\ast }$
on the aspect ratio (figure 4
a), whereas it is much more sensitive to changes in slope angle (figure 4
b). There are singularities in the governing equations at the lower and upper slope-angle limits (
${\it\zeta}_{w}^{\ast }$
on the aspect ratio (figure 4
a), whereas it is much more sensitive to changes in slope angle (figure 4
b). There are singularities in the governing equations at the lower and upper slope-angle limits (
![]() ${\it\zeta}={\it\zeta}_{1}$
and
${\it\zeta}={\it\zeta}_{1}$
and
![]() ${\it\zeta}={\it\zeta}_{2}$
, respectively) which make numerical computations difficult close to these values, and consequently the results shown in figure 4(b) do not extend across the whole range
${\it\zeta}={\it\zeta}_{2}$
, respectively) which make numerical computations difficult close to these values, and consequently the results shown in figure 4(b) do not extend across the whole range
![]() ${\it\zeta}_{1}<{\it\zeta}<{\it\zeta}_{2}$
.
${\it\zeta}_{1}<{\it\zeta}<{\it\zeta}_{2}$
.

Figure 4. Phase diagrams showing the values of the wall-friction angle
![]() ${\it\zeta}_{w}$
that correspond to slip velocities at the sidewalls (white) or no slip (shaded) for (a) varying the aspect ratio
${\it\zeta}_{w}$
that correspond to slip velocities at the sidewalls (white) or no slip (shaded) for (a) varying the aspect ratio
![]() ${\it\varepsilon}$
(for a fixed slope angle
${\it\varepsilon}$
(for a fixed slope angle
![]() ${\it\zeta}=26^{\circ }$
) and (b) varying the slope angle (for a fixed
${\it\zeta}=26^{\circ }$
) and (b) varying the slope angle (for a fixed
![]() ${\it\varepsilon}=0.1$
). Solid lines denote where the wall-friction angle is equal to the critical value
${\it\varepsilon}=0.1$
). Solid lines denote where the wall-friction angle is equal to the critical value
![]() ${\it\zeta}_{w}={\it\zeta}_{w}^{\ast }$
.
${\it\zeta}_{w}={\it\zeta}_{w}^{\ast }$
.
It should be noted that using the full extended friction law of Pouliquen & Forterre (Reference Pouliquen and Forterre2002), rather than the basic form (4.18), to solve (4.17) will change the velocity profiles shown in figures 2 and 3. Close to the frictional walls, where the velocities are low, the material will be in the static or intermediate regime and the switching point will depend on the local Froude number, meaning that the system is no longer independent of scale.
5. Reconstructing the full velocity field
The full steady uniform velocity field
![]() $u(y,z)$
in a cross-section of the channel can be reconstructed from the dimensional depth-averaged values
$u(y,z)$
in a cross-section of the channel can be reconstructed from the dimensional depth-averaged values
![]() $\bar{u}(y)$
by assuming a vertical profile through the avalanche depth, i.e.
$\bar{u}(y)$
by assuming a vertical profile through the avalanche depth, i.e.
where
![]() $\hat{z}=z/h_{0}$
is the rescaled vertical coordinate and
$\hat{z}=z/h_{0}$
is the rescaled vertical coordinate and
![]() $f$
is the vertical shape profile, which is taken to be independent of the transverse coordinate
$f$
is the vertical shape profile, which is taken to be independent of the transverse coordinate
![]() $y$
. In order to be consistent with the definition (2.1), this profile must satisfy the condition
$y$
. In order to be consistent with the definition (2.1), this profile must satisfy the condition
and physically one anticipates a flow moving faster at the surface, meaning
![]() $f$
should be a non-decreasing function. There are families of linear shear profiles satisfying these requirements, which have previously been used to reconstruct the internal velocities at the United States Geological Survey (USGS) debris flow flume (Johnson et al.
Reference Johnson, Kokelaar, Iverson, Logan, LaHusen and Gray2012) and derive depth-averaged segregation equations (Gray & Kokelaar Reference Gray and Kokelaar2010a
,Reference Gray and Kokelaar
b
). GDR MiDi (Reference GDR MiDi2004) showed with experimental measurements and discrete element simulations that the profiles are nonlinear, with the exact form depending on the width of the chute. Jop et al. (Reference Jop, Forterre and Pouliquen2005) developed this idea further, deriving a width-averaged
$f$
should be a non-decreasing function. There are families of linear shear profiles satisfying these requirements, which have previously been used to reconstruct the internal velocities at the United States Geological Survey (USGS) debris flow flume (Johnson et al.
Reference Johnson, Kokelaar, Iverson, Logan, LaHusen and Gray2012) and derive depth-averaged segregation equations (Gray & Kokelaar Reference Gray and Kokelaar2010a
,Reference Gray and Kokelaar
b
). GDR MiDi (Reference GDR MiDi2004) showed with experimental measurements and discrete element simulations that the profiles are nonlinear, with the exact form depending on the width of the chute. Jop et al. (Reference Jop, Forterre and Pouliquen2005) developed this idea further, deriving a width-averaged
![]() ${\it\mu}(I)$
-rheology and solving for the velocity profile through the avalanche depth. To be consistent with the assumptions used in § 2 (in depth-integrating the deviatoric stress terms), a Bagnold profile is chosen here,
${\it\mu}(I)$
-rheology and solving for the velocity profile through the avalanche depth. To be consistent with the assumptions used in § 2 (in depth-integrating the deviatoric stress terms), a Bagnold profile is chosen here,
The expression (5.3) may be obtained by dividing the steady-uniform Bagnold solution (2.18) by the depth-averaged Bagnold velocity (2.19). Figure 5 shows example plots of the full velocity field
![]() $\hat{u} ({\hat{y}},\hat{z})$
, reconstructed from the depth-averaged values using (5.1) and (5.3). The variables are made non-dimensional using the same scalings (4.16), together with
$\hat{u} ({\hat{y}},\hat{z})$
, reconstructed from the depth-averaged values using (5.1) and (5.3). The variables are made non-dimensional using the same scalings (4.16), together with
![]() $z=h_{0}\hat{z}$
for the vertical coordinate. In figure 5(a,b) slip boundary conditions (4.20), (4.21) are imposed in a wide channel, whereas figure 5(c,d) shows solutions in a narrower channel with no-slip boundary conditions (4.19).
$z=h_{0}\hat{z}$
for the vertical coordinate. In figure 5(a,b) slip boundary conditions (4.20), (4.21) are imposed in a wide channel, whereas figure 5(c,d) shows solutions in a narrower channel with no-slip boundary conditions (4.19).

Figure 5. Steady uniform downslope velocity profiles
![]() $\hat{u} ({\hat{y}},\hat{z})$
, reconstructed from the depth-averaged values using the Bagnold solution (5.3): (a,b) show a wide channel of aspect ratio
$\hat{u} ({\hat{y}},\hat{z})$
, reconstructed from the depth-averaged values using the Bagnold solution (5.3): (a,b) show a wide channel of aspect ratio
![]() ${\it\varepsilon}=0.01$
, solved with slip boundary conditions with wall-friction angle
${\it\varepsilon}=0.01$
, solved with slip boundary conditions with wall-friction angle
![]() ${\it\zeta}_{w}=7^{\circ }$
, whereas the channel in (c,d) is narrower (
${\it\zeta}_{w}=7^{\circ }$
, whereas the channel in (c,d) is narrower (
![]() ${\it\varepsilon}=0.1$
) and is solved with no-slip boundary conditions at the walls. Both chutes are inclined at an angle
${\it\varepsilon}=0.1$
) and is solved with no-slip boundary conditions at the walls. Both chutes are inclined at an angle
![]() ${\it\zeta}=26^{\circ }$
. Black lines on the left-hand panels (a,c) mark where the velocity is equal to the mean velocity
${\it\zeta}=26^{\circ }$
. Black lines on the left-hand panels (a,c) mark where the velocity is equal to the mean velocity
![]() $\hat{u} _{f}$
, given by expression (5.5) made non-dimensional with (4.8), with particles above travelling downslope faster than the mean flow and those below moving slower. The mean velocities are
$\hat{u} _{f}$
, given by expression (5.5) made non-dimensional with (4.8), with particles above travelling downslope faster than the mean flow and those below moving slower. The mean velocities are
![]() $\hat{u} _{f}=0.983$
when
$\hat{u} _{f}=0.983$
when
![]() ${\it\varepsilon}=0.01$
and
${\it\varepsilon}=0.01$
and
![]() $\hat{u} _{f}=0.811$
when
$\hat{u} _{f}=0.811$
when
![]() ${\it\varepsilon}=0.1$
. The right-hand panels (b,d) show the velocity at the left-hand boundary
${\it\varepsilon}=0.1$
. The right-hand panels (b,d) show the velocity at the left-hand boundary
![]() ${\hat{y}}=0$
and centreline
${\hat{y}}=0$
and centreline
![]() ${\hat{y}}=0.5$
(solid bold lines), and at uniformly spaced intervals of width 0.05 in between (dashed lines).
${\hat{y}}=0.5$
(solid bold lines), and at uniformly spaced intervals of width 0.05 in between (dashed lines).
At this point, it is useful to define additional quantities that will be used to examine the full velocity fields in later sections. In an analogous way to the depth-averaged value (2.1), the width-averaged downslope velocity is given by
The mean downslope velocity, which is a combination of the width- and depth-averaging processes, can also be defined as
where (5.1) and (5.2) have been used to simplify the double integral. The lines where
![]() $u=u_{f}$
have been plotted on figure 5. Material above these lines moves downslope faster than the mean flow
$u=u_{f}$
have been plotted on figure 5. Material above these lines moves downslope faster than the mean flow
![]() $u_{f}$
, whilst below it moves downslope slower. In experiments and industrial applications, the flux of material through the channel is also important. The total volume flux is given by
$u_{f}$
, whilst below it moves downslope slower. In experiments and industrial applications, the flux of material through the channel is also important. The total volume flux is given by
and the corresponding mass flux is
where
![]() ${\it\rho}^{\ast }=2550$
kg m
${\it\rho}^{\ast }=2550$
kg m
![]() $^{-3}$
is the intrinsic density of ballotini and
$^{-3}$
is the intrinsic density of ballotini and
![]() ${\it\Phi}=0.6$
is the solid volume fraction. In the inviscid case (when
${\it\Phi}=0.6$
is the solid volume fraction. In the inviscid case (when
![]() $\bar{u}(y)=\bar{u}_{0}$
), the integrals in (5.5) and (5.6) can be evaluated explicitly, giving a mass flux of
$\bar{u}(y)=\bar{u}_{0}$
), the integrals in (5.5) and (5.6) can be evaluated explicitly, giving a mass flux of
Whilst the internal flow characteristics are difficult to measure experimentally, surface velocity profiles,
![]() $u_{s}(y)$
, can be obtained (e.g. Jop et al.
Reference Jop, Forterre and Pouliquen2005) and compared with the new theoretical values, which are given by
$u_{s}(y)$
, can be obtained (e.g. Jop et al.
Reference Jop, Forterre and Pouliquen2005) and compared with the new theoretical values, which are given by
6. Comparison with the full
 ${\it\mu}(I)$
-rheology
${\it\mu}(I)$
-rheology
The reconstructed depth-averaged values are now compared with those predicted by the full, three-dimensional
![]() ${\it\mu}(I)$
-rheology. These equations have previously been solved for the chute-flow geometry with no-slip boundary conditions (Jop et al.
Reference Jop, Forterre and Pouliquen2006; Pouliquen et al.
Reference Pouliquen, Cassar, Jop, Forterre and Nicolas2006), and the results have been checked for consistency against Jop et al. (Reference Jop, Forterre and Pouliquen2006). Here, we will generalize the problem to both no slip and Coulomb slip at the sidewalls and show that the non-dimensionalised problems in both cases are scale invariant. The (dimensional) incompressibility condition and conservation of momentum may be written in compact notation as
${\it\mu}(I)$
-rheology. These equations have previously been solved for the chute-flow geometry with no-slip boundary conditions (Jop et al.
Reference Jop, Forterre and Pouliquen2006; Pouliquen et al.
Reference Pouliquen, Cassar, Jop, Forterre and Nicolas2006), and the results have been checked for consistency against Jop et al. (Reference Jop, Forterre and Pouliquen2006). Here, we will generalize the problem to both no slip and Coulomb slip at the sidewalls and show that the non-dimensionalised problems in both cases are scale invariant. The (dimensional) incompressibility condition and conservation of momentum may be written in compact notation as
Defining a function
![]() $F^{s}(x,y,t)=z-h(x,y,t)$
and unit normal
$F^{s}(x,y,t)=z-h(x,y,t)$
and unit normal
![]() $\boldsymbol{n}^{s}=\boldsymbol{{\rm\nabla}}F^{s}/|\boldsymbol{{\rm\nabla}}F^{s}|$
, one can impose kinematic boundary conditions at the free surface,
$\boldsymbol{n}^{s}=\boldsymbol{{\rm\nabla}}F^{s}/|\boldsymbol{{\rm\nabla}}F^{s}|$
, one can impose kinematic boundary conditions at the free surface,
where the superscripts denote the velocity field evaluated at the top of the flow,
![]() $z=h(x,y,t)$
. A traction-free condition is also imposed at the free surface,
$z=h(x,y,t)$
. A traction-free condition is also imposed at the free surface,
where
![]() ${\bf\sigma}^{s}$
is the Cauchy stress tensor (2.8) calculated at the top of the flow. Finally, a no-slip condition is specified at the base,
${\bf\sigma}^{s}$
is the Cauchy stress tensor (2.8) calculated at the top of the flow. Finally, a no-slip condition is specified at the base,
In general, there will also be a kinematic boundary condition, similar to (6.4), at the base of the flow, but the no-slip condition (6.6) and rigid base ensure it is automatically satisfied.
Now consider a simple chute-flow configuration. In the steady, fully-developed regime, the variables are independent of time
![]() $t$
and downslope position
$t$
and downslope position
![]() $x$
. It is also assumed that the flow is unidirectional in the downslope direction, so solutions are sought of the form
$x$
. It is also assumed that the flow is unidirectional in the downslope direction, so solutions are sought of the form
With this ansatz, it is straightforward to see that conservation of mass (6.1) is automatically satisfied. The strain-rate tensor
![]() $\unicode[STIX]{x1D63F}$
simplifies to
$\unicode[STIX]{x1D63F}$
simplifies to
 $$\begin{eqnarray}\unicode[STIX]{x1D63F}=\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D60B}_{xx} & \unicode[STIX]{x1D60B}_{xy} & \unicode[STIX]{x1D60B}_{xz}\\ \unicode[STIX]{x1D60B}_{yx} & \unicode[STIX]{x1D60B}_{yy} & \unicode[STIX]{x1D60B}_{yz}\\ \unicode[STIX]{x1D60B}_{zx} & \unicode[STIX]{x1D60B}_{zy} & \unicode[STIX]{x1D60B}_{zz}\end{array}\right)=\left(\begin{array}{@{}ccc@{}}0 & \displaystyle \frac{1}{2}\frac{\partial u}{\partial y} & \displaystyle \frac{1}{2}\frac{\partial u}{\partial z}\\ \displaystyle \frac{1}{2}\frac{\partial u}{\partial y} & 0 & 0\\ \displaystyle \frac{1}{2}\frac{\partial u}{\partial z} & 0 & 0\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D63F}=\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D60B}_{xx} & \unicode[STIX]{x1D60B}_{xy} & \unicode[STIX]{x1D60B}_{xz}\\ \unicode[STIX]{x1D60B}_{yx} & \unicode[STIX]{x1D60B}_{yy} & \unicode[STIX]{x1D60B}_{yz}\\ \unicode[STIX]{x1D60B}_{zx} & \unicode[STIX]{x1D60B}_{zy} & \unicode[STIX]{x1D60B}_{zz}\end{array}\right)=\left(\begin{array}{@{}ccc@{}}0 & \displaystyle \frac{1}{2}\frac{\partial u}{\partial y} & \displaystyle \frac{1}{2}\frac{\partial u}{\partial z}\\ \displaystyle \frac{1}{2}\frac{\partial u}{\partial y} & 0 & 0\\ \displaystyle \frac{1}{2}\frac{\partial u}{\partial z} & 0 & 0\end{array}\right),\end{eqnarray}$$
meaning that the second invariant is
From the normal component of the momentum balance (6.2), and the fact that the pressure at the free surface is zero (i.e. the normal component of the traction-free condition (6.5)), the lithostatic pressure distribution (2.15) is recovered,
The transverse component of the momentum equation (6.2) gives
![]() $\partial p/\partial y=0$
, meaning the pressure, and consequently height, are independent of transverse position
$\partial p/\partial y=0$
, meaning the pressure, and consequently height, are independent of transverse position
![]() $y$
,
$y$
,
This is consistent with the depth-averaged theory (4.4). Note that a steady flow with non-uniform free surface must have non-zero transverse or normal velocities, i.e. the ansatz (6.7) cannot hold in this case. The kinematic boundary condition (6.4) is automatically satisfied, as is the transverse component of the stress-free condition (6.5). The downslope component of the traction-free condition becomes
which needs to be treated carefully due to potential singularities at the free surface. If it is assumed that
![]() $\Vert \unicode[STIX]{x1D63F}\Vert >0$
(which is true provided that
$\Vert \unicode[STIX]{x1D63F}\Vert >0$
(which is true provided that
![]() $\partial u/\partial y$
and
$\partial u/\partial y$
and
![]() $\partial u/\partial z$
are not both identically zero), then the inertial number
$\partial u/\partial z$
are not both identically zero), then the inertial number
![]() $I\rightarrow \infty$
because the pressure is zero at the free surface. Fortunately, the function
$I\rightarrow \infty$
because the pressure is zero at the free surface. Fortunately, the function
![]() ${\it\mu}(I)$
remains well defined and bounded, with
${\it\mu}(I)$
remains well defined and bounded, with
![]() ${\it\mu}(I)\rightarrow {\it\mu}_{2}$
. The viscosity
${\it\mu}(I)\rightarrow {\it\mu}_{2}$
. The viscosity
![]() ${\it\eta}$
is then zero when
${\it\eta}$
is then zero when
![]() $z=h_{0}$
, so the condition (6.12) is automatically satisfied. The problem reduces to solving an elliptic scalar PDE, which comes from the downslope component of the momentum equation (6.2):
$z=h_{0}$
, so the condition (6.12) is automatically satisfied. The problem reduces to solving an elliptic scalar PDE, which comes from the downslope component of the momentum equation (6.2):
where the rescaled viscosity
![]() ${\it\eta}^{\prime }$
is given explicitly by
${\it\eta}^{\prime }$
is given explicitly by
 $$\begin{eqnarray}{\it\eta}^{\prime }=\frac{{\it\mu}(I)(h_{0}-z)}{\displaystyle \left(\left(\frac{\partial u}{\partial y}\right)^{2}+\left(\frac{\partial u}{\partial z}\right)^{2}\right)^{1/2}},\end{eqnarray}$$
$$\begin{eqnarray}{\it\eta}^{\prime }=\frac{{\it\mu}(I)(h_{0}-z)}{\displaystyle \left(\left(\frac{\partial u}{\partial y}\right)^{2}+\left(\frac{\partial u}{\partial z}\right)^{2}\right)^{1/2}},\end{eqnarray}$$
and the inertial number
![]() $I$
is
$I$
is
 $$\begin{eqnarray}I=\frac{d\displaystyle \left(\left(\frac{\partial u}{\partial y}\right)^{2}+\left(\frac{\partial u}{\partial z}\right)^{2}\right)^{1/2}}{\sqrt{{\it\Phi}g\cos {\it\zeta}(h_{0}-z)}}.\end{eqnarray}$$
$$\begin{eqnarray}I=\frac{d\displaystyle \left(\left(\frac{\partial u}{\partial y}\right)^{2}+\left(\frac{\partial u}{\partial z}\right)^{2}\right)^{1/2}}{\sqrt{{\it\Phi}g\cos {\it\zeta}(h_{0}-z)}}.\end{eqnarray}$$
Equation (6.13) is solved subject to the no-slip boundary condition at the base of the flow,
As in the depth-averaged case, the boundary conditions at the lateral sidewalls may take different forms. The simplest is to take no-slip conditions,
which may be most appropriate for rough walls. For smoother walls there will be a slip velocity at the boundaries, which in turn will induce a stress. Denoting this stress as
![]() ${\it\tau}_{w}$
and assuming basic Coulomb slip (as in § 4) leads to
${\it\tau}_{w}$
and assuming basic Coulomb slip (as in § 4) leads to
where
![]() $u_{w}(z)=u(0,z)=u(W,z)$
is the wall slip velocity (not to be confused with the width-averaged profile (5.4)). From the governing equations, the stress at the wall must also be equal to
$u_{w}(z)=u(0,z)=u(W,z)$
is the wall slip velocity (not to be confused with the width-averaged profile (5.4)). From the governing equations, the stress at the wall must also be equal to
where
![]() $\boldsymbol{n}$
is the outward facing normal,
$\boldsymbol{n}$
is the outward facing normal,
![]() $\boldsymbol{i}$
is the unit vector in the downslope direction and
$\boldsymbol{i}$
is the unit vector in the downslope direction and
![]() ${\bf\tau}$
is the deviatoric stress tensor. Taking the unit normal to be
${\bf\tau}$
is the deviatoric stress tensor. Taking the unit normal to be
![]() $\boldsymbol{n}=-\boldsymbol{j}$
at
$\boldsymbol{n}=-\boldsymbol{j}$
at
![]() $y=0$
and
$y=0$
and
![]() $\boldsymbol{n}=\boldsymbol{j}$
at
$\boldsymbol{n}=\boldsymbol{j}$
at
![]() $y=W$
, and using the simplified strain-rate tensor (6.8) gives
$y=W$
, and using the simplified strain-rate tensor (6.8) gives
 $$\begin{eqnarray}{\it\tau}_{w}=\left\{\begin{array}{@{}ll@{}}\displaystyle -\frac{{\it\mu}(I){\it\rho}g\cos {\it\zeta}(h_{0}-z)}{2\Vert \unicode[STIX]{x1D63F}\Vert }\frac{\partial u}{\partial y}\quad & \text{at}~y=0,\\ \displaystyle \frac{{\it\mu}(I){\it\rho}g\cos {\it\zeta}(h_{0}-z)}{2\Vert \unicode[STIX]{x1D63F}\Vert }\frac{\partial u}{\partial y}\quad & \text{at}~y=W.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\it\tau}_{w}=\left\{\begin{array}{@{}ll@{}}\displaystyle -\frac{{\it\mu}(I){\it\rho}g\cos {\it\zeta}(h_{0}-z)}{2\Vert \unicode[STIX]{x1D63F}\Vert }\frac{\partial u}{\partial y}\quad & \text{at}~y=0,\\ \displaystyle \frac{{\it\mu}(I){\it\rho}g\cos {\it\zeta}(h_{0}-z)}{2\Vert \unicode[STIX]{x1D63F}\Vert }\frac{\partial u}{\partial y}\quad & \text{at}~y=W.\end{array}\right.\end{eqnarray}$$
Equating the two expressions (6.18), (6.20) leads to the boundary conditions
6.1. Non-dimensionalisation
As for the depth-averaged governing equations, the full rheology is now made non-dimensional by introducing the scalings
where the hats denote dimensionless quantities. The downslope momentum balance (6.13) then reduces to
where
![]() ${\it\varepsilon}=h_{0}/W$
is the channel aspect ratio as before and the rescaled viscosity
${\it\varepsilon}=h_{0}/W$
is the channel aspect ratio as before and the rescaled viscosity
![]() $\hat{{\it\eta}}$
is given by
$\hat{{\it\eta}}$
is given by
 $$\begin{eqnarray}\hat{{\it\eta}}=\frac{{\it\mu}(I)(1-\hat{z})}{\displaystyle \left({\it\varepsilon}^{2}\left(\frac{\partial \hat{u} }{\partial {\hat{y}}}\right)^{2}+\left(\frac{\partial \hat{u} }{\partial \hat{z}}\right)^{2}\right)^{1/2}}.\end{eqnarray}$$
$$\begin{eqnarray}\hat{{\it\eta}}=\frac{{\it\mu}(I)(1-\hat{z})}{\displaystyle \left({\it\varepsilon}^{2}\left(\frac{\partial \hat{u} }{\partial {\hat{y}}}\right)^{2}+\left(\frac{\partial \hat{u} }{\partial \hat{z}}\right)^{2}\right)^{1/2}}.\end{eqnarray}$$
The inertial number
![]() $I$
is already non-dimensional, by definition, but may be written in terms of the other dimensionless variables as
$I$
is already non-dimensional, by definition, but may be written in terms of the other dimensionless variables as
 $$\begin{eqnarray}I=\frac{2I_{0}\displaystyle \left({\it\varepsilon}^{2}\!\left(\frac{\partial \hat{u} }{\partial {\hat{y}}}\right)^{2}+\left(\frac{\partial \hat{u} }{\partial \hat{z}}\right)^{2}\right)^{1/2}}{5{\it\gamma}(1-\hat{z})^{1/2}},\end{eqnarray}$$
$$\begin{eqnarray}I=\frac{2I_{0}\displaystyle \left({\it\varepsilon}^{2}\!\left(\frac{\partial \hat{u} }{\partial {\hat{y}}}\right)^{2}+\left(\frac{\partial \hat{u} }{\partial \hat{z}}\right)^{2}\right)^{1/2}}{5{\it\gamma}(1-\hat{z})^{1/2}},\end{eqnarray}$$
where the steady uniform velocity (4.8) and the definition of
![]() $I_{0}$
(2.14) have been used to simplify (6.26). The no-slip boundary conditions (6.16) and (6.17) at the base and sidewalls become
$I_{0}$
(2.14) have been used to simplify (6.26). The no-slip boundary conditions (6.16) and (6.17) at the base and sidewalls become
and
respectively, and the alternative slip conditions (6.21) and (6.22) are

Figure 6. Steady, uniform, downslope velocity profiles
![]() $\hat{u} ({\hat{y}},\hat{z})$
, calculated by solving the full
$\hat{u} ({\hat{y}},\hat{z})$
, calculated by solving the full
![]() ${\it\mu}(I)$
-rheology (6.24)–(6.26): (a,b) show a wide channel (aspect ratio
${\it\mu}(I)$
-rheology (6.24)–(6.26): (a,b) show a wide channel (aspect ratio
![]() ${\it\varepsilon}=0.01$
), solved with slip boundary conditions (6.29), (6.30) with wall-friction angle
${\it\varepsilon}=0.01$
), solved with slip boundary conditions (6.29), (6.30) with wall-friction angle
![]() ${\it\zeta}_{w}=7^{\circ }$
, whereas the channel in (c,d) is narrower (
${\it\zeta}_{w}=7^{\circ }$
, whereas the channel in (c,d) is narrower (
![]() ${\it\varepsilon}=0.1$
) and is solved with no-slip boundary conditions (6.28) at the walls. Both chutes are inclined at an angle
${\it\varepsilon}=0.1$
) and is solved with no-slip boundary conditions (6.28) at the walls. Both chutes are inclined at an angle
![]() ${\it\zeta}=26^{\circ }$
. Black lines on the left-hand panels (a,c) mark where the velocity is equal to the mean velocity
${\it\zeta}=26^{\circ }$
. Black lines on the left-hand panels (a,c) mark where the velocity is equal to the mean velocity
![]() $\hat{u} _{f}$
, with
$\hat{u} _{f}$
, with
![]() $\hat{u} _{f}=0.987$
when
$\hat{u} _{f}=0.987$
when
![]() ${\it\varepsilon}=0.01$
and
${\it\varepsilon}=0.01$
and
![]() $\hat{u} _{f}=0.755$
when
$\hat{u} _{f}=0.755$
when
![]() ${\it\varepsilon}=0.1$
. The right-hand panels (b,d) show the velocity at the left-hand boundary
${\it\varepsilon}=0.1$
. The right-hand panels (b,d) show the velocity at the left-hand boundary
![]() ${\hat{y}}=0$
and centreline
${\hat{y}}=0$
and centreline
![]() ${\hat{y}}=0.5$
(solid lines), and at uniformly spaced intervals of width 0.05 in between (dashed lines).
${\hat{y}}=0.5$
(solid lines), and at uniformly spaced intervals of width 0.05 in between (dashed lines).

Figure 7. Comparison between the depth-averaged theory (solid lines) and steady-state solutions of the full three-dimensional
![]() ${\it\mu}(I)$
-rheology (dashed lines) for the two different channels and boundary conditions described in figures 5 and 6. Plots show the depth-averaged downslope velocity
${\it\mu}(I)$
-rheology (dashed lines) for the two different channels and boundary conditions described in figures 5 and 6. Plots show the depth-averaged downslope velocity
![]() $\hat{\bar{u}}({\hat{y}})$
.
$\hat{\bar{u}}({\hat{y}})$
.

Figure 8. Plots of the width-averaged velocity
![]() $\hat{u} _{W}(\hat{z})$
, defined by (5.4) and scalings (6.23), for the two different channels and boundary conditions shown in figures 5 and 6. Solid lines denote the reconstructed depth-averaged theory and dashed lines are steady-state solutions of the full three-dimensional
$\hat{u} _{W}(\hat{z})$
, defined by (5.4) and scalings (6.23), for the two different channels and boundary conditions shown in figures 5 and 6. Solid lines denote the reconstructed depth-averaged theory and dashed lines are steady-state solutions of the full three-dimensional
![]() ${\it\mu}(I)$
-rheology.
${\it\mu}(I)$
-rheology.
Despite these similarities, the two approaches are not formally equivalent. If this was the case there would be separable solutions to (6.24) of the form
![]() $\hat{u} ({\hat{y}},\hat{z})=\hat{\bar{u}}({\hat{y}})f(\hat{z})$
, where
$\hat{u} ({\hat{y}},\hat{z})=\hat{\bar{u}}({\hat{y}})f(\hat{z})$
, where
![]() $\hat{\bar{u}}$
satisfies the ODE (4.17) and
$\hat{\bar{u}}$
satisfies the ODE (4.17) and
![]() $f$
is the Bagnold velocity profile (5.3). Not only do such solutions not exist, but constructing any separable solutions to the full PDE does not seem possible. Furthermore, if one assumes a Bagnold-like depth-dependence the different slip boundary conditions (4.20), (4.21) and (6.29), (6.30) are not obviously compatible. These results are not suprising because, although the depth-averaged rheology is based on the full constitutive law, the derivation is largely heuristic and therefore one would not expect formal agreement.
$f$
is the Bagnold velocity profile (5.3). Not only do such solutions not exist, but constructing any separable solutions to the full PDE does not seem possible. Furthermore, if one assumes a Bagnold-like depth-dependence the different slip boundary conditions (4.20), (4.21) and (6.29), (6.30) are not obviously compatible. These results are not suprising because, although the depth-averaged rheology is based on the full constitutive law, the derivation is largely heuristic and therefore one would not expect formal agreement.
Equation (6.24) is solved numerically using finite element methods and the software package FreeFem++ (Hecht Reference Hecht2012), and the resulting velocity fields
![]() $\hat{u} ({\hat{y}},\hat{z})$
are shown on figure 6. The two regimes investigated correspond to the depth-averaged theory of figure 5, allowing comparisons to be drawn between the different theories. Slip boundary conditions (4.20), (4.21) and (6.29), (6.30) are imposed with a wall-friction angle
$\hat{u} ({\hat{y}},\hat{z})$
are shown on figure 6. The two regimes investigated correspond to the depth-averaged theory of figure 5, allowing comparisons to be drawn between the different theories. Slip boundary conditions (4.20), (4.21) and (6.29), (6.30) are imposed with a wall-friction angle
![]() ${\it\zeta}_{w}=7^{\circ }$
for a wide channel of aspect ratio
${\it\zeta}_{w}=7^{\circ }$
for a wide channel of aspect ratio
![]() ${\it\varepsilon}=0.01$
(figures 5
a,b and 6
a,b). The mean velocities
${\it\varepsilon}=0.01$
(figures 5
a,b and 6
a,b). The mean velocities
![]() $\hat{u} _{f}$
(defined by (5.5) made non-dimensional with
$\hat{u} _{f}$
(defined by (5.5) made non-dimensional with
![]() $\bar{u}_{0}$
) show excellent agreement, with
$\bar{u}_{0}$
) show excellent agreement, with
![]() $\hat{u} _{f}=0.983$
for the depth-averaged theory and
$\hat{u} _{f}=0.983$
for the depth-averaged theory and
![]() $\hat{u} _{f}=0.987$
for the
$\hat{u} _{f}=0.987$
for the
![]() ${\it\mu}(I)$
-rheology. This suggests that the new theory is a good approximation to the full constitutive law for sufficiently shallow flows. Figures 7 and 8, showing the depth- and width-averaged velocities, provide further evidence to support this, with both sets of profiles closely coinciding with each other. There is a slight discrepancy in the sidewall slip velocities, with the depth-averaged theory predicting less slip than the full rheology. This can be seen on figures 5(b) and 6(b), showing the vertical dependence of the velocity at uniformly-spaced transverse positions. The values are identical near the centre of the channel but towards the boundaries the full
${\it\mu}(I)$
-rheology. This suggests that the new theory is a good approximation to the full constitutive law for sufficiently shallow flows. Figures 7 and 8, showing the depth- and width-averaged velocities, provide further evidence to support this, with both sets of profiles closely coinciding with each other. There is a slight discrepancy in the sidewall slip velocities, with the depth-averaged theory predicting less slip than the full rheology. This can be seen on figures 5(b) and 6(b), showing the vertical dependence of the velocity at uniformly-spaced transverse positions. The values are identical near the centre of the channel but towards the boundaries the full
![]() ${\it\mu}(I)$
-rheology produces larger slip velocities. The effect is more pronounced close to the free surface, with figure 8 showing the full rheology width-averaged profiles taking slightly faster values in the upper regions.
${\it\mu}(I)$
-rheology produces larger slip velocities. The effect is more pronounced close to the free surface, with figure 8 showing the full rheology width-averaged profiles taking slightly faster values in the upper regions.
A narrower channel (aspect ratio
![]() ${\it\varepsilon}=0.1$
) is shown on figures 5(c,d) and 6(c,d), where the no-slip boundary conditions (4.19) and (6.28) are now imposed at the sidewalls. The agreement is less impressive in this case, with the mean values
${\it\varepsilon}=0.1$
) is shown on figures 5(c,d) and 6(c,d), where the no-slip boundary conditions (4.19) and (6.28) are now imposed at the sidewalls. The agreement is less impressive in this case, with the mean values
![]() $\hat{u} _{f}=0.811$
for depth-averaged and
$\hat{u} _{f}=0.811$
for depth-averaged and
![]() $\hat{u} _{f}=0.755$
for full rheology indicating that the new theory is overestimating the velocities in this regime. This is also apparent from the depth-averaged profiles in figure 7 and width-averaged values in figure 8. The structure near the lateral boundaries is slightly different, with steeper transverse gradients in the depth-averaged case ensuring that the frictional walls act locally and have less of an overall effect on the flow. At the centre of the channel both theories show Bagnold-like depth-dependence (2.18) (figures 5
d and 6
d), but, as one moves towards the walls, the full rheology profiles change dramatically and become concave in places. This behaviour is captured in figure 8, where the width-averaged profiles
$\hat{u} _{f}=0.755$
for full rheology indicating that the new theory is overestimating the velocities in this regime. This is also apparent from the depth-averaged profiles in figure 7 and width-averaged values in figure 8. The structure near the lateral boundaries is slightly different, with steeper transverse gradients in the depth-averaged case ensuring that the frictional walls act locally and have less of an overall effect on the flow. At the centre of the channel both theories show Bagnold-like depth-dependence (2.18) (figures 5
d and 6
d), but, as one moves towards the walls, the full rheology profiles change dramatically and become concave in places. This behaviour is captured in figure 8, where the width-averaged profiles
![]() $\hat{u} _{W}(\hat{z})$
(defined by (5.4) non-dimensionalised with
$\hat{u} _{W}(\hat{z})$
(defined by (5.4) non-dimensionalised with
![]() $\bar{u}_{0}$
) are shown for the two theories. By construction, the depth-averaged theory gives a scaled Bagnold solution, but the full profiles are more linear in nature. Interestingly, although the surface velocities for the full rheology are slower at the centre of the channel, the width-averaged values are actually faster at the surface. This is due to the different structure near the boundaries having an impact on the overall flow characteristics.
$\bar{u}_{0}$
) are shown for the two theories. By construction, the depth-averaged theory gives a scaled Bagnold solution, but the full profiles are more linear in nature. Interestingly, although the surface velocities for the full rheology are slower at the centre of the channel, the width-averaged values are actually faster at the surface. This is due to the different structure near the boundaries having an impact on the overall flow characteristics.
7. Experimental results
Small-scale laboratory experiments are used to further validate the depth-averaged theoretical results. The experimental configuration consists of Perspex sidewalls attached to a 1.5 m long chute in such a way that the channel width
![]() $W$
may be continuously varied from 15 to 600 mm. The base of the chute is flat and roughened with one layer of glass ballotini (750–1000
$W$
may be continuously varied from 15 to 600 mm. The base of the chute is flat and roughened with one layer of glass ballotini (750–1000
![]() ${\rm\mu}$
m) stuck on with double-sided tape. It can be inclined from the horizontal up to angles of
${\rm\mu}$
m) stuck on with double-sided tape. It can be inclined from the horizontal up to angles of
![]() ${\it\zeta}=60^{\circ }$
. Experiments are carried out using spherical glass ballotini (75–150
${\it\zeta}=60^{\circ }$
. Experiments are carried out using spherical glass ballotini (75–150
![]() ${\rm\mu}$
m), released from rest using a hopper and moveable gate, allowing the inflow thickness to be varied between 1 and 15 mm. A laser profilometer records the flow thickness for a 100 mm section of chute at a distance 800 mm downstream. It may be mounted cross slope, showing a near-constant transverse thickness profile in agreement with (4.4), or along the downslope centreline to check the steady uniform nature of the flow. The thickness data is averaged in space and time to give a single value
${\rm\mu}$
m), released from rest using a hopper and moveable gate, allowing the inflow thickness to be varied between 1 and 15 mm. A laser profilometer records the flow thickness for a 100 mm section of chute at a distance 800 mm downstream. It may be mounted cross slope, showing a near-constant transverse thickness profile in agreement with (4.4), or along the downslope centreline to check the steady uniform nature of the flow. The thickness data is averaged in space and time to give a single value
![]() $h_{0}$
for each experiment.
$h_{0}$
for each experiment.
The material is free to flow off the end of the chute where a balance measures the outflow mass flux
![]() $M$
. Assuming there is no erosion or deposition once the steady state has been set up,
$M$
. Assuming there is no erosion or deposition once the steady state has been set up,
![]() $M$
corresponds to the mass flux through the channel itself and is given by the theoretical expressions (5.6) and (5.7). The relationship between
$M$
corresponds to the mass flux through the channel itself and is given by the theoretical expressions (5.6) and (5.7). The relationship between
![]() $M$
and the flow thickness
$M$
and the flow thickness
![]() $h_{0}$
is calculated for a variety of chute widths and inclination angles and is shown in figure 9(a). Also shown for reference, with dashed lines, are the fluxes of the inviscid theory (5.8). Reasonable quantitative agreement is found for all experiments, although for the wider channels there is little difference between the viscous and inviscid theories and it could be argued that both fit the data equally well. This is because the small aspect ratios in these cases mean that the depth-averaged velocity profiles only differ in thin boundary layers that do not significantly contribute to the overall flux. The difference is more pronounced in narrower channels with larger aspect ratios, since the viscous velocity profiles begin to diverge from the inviscid theory, and for a channel of width
$h_{0}$
is calculated for a variety of chute widths and inclination angles and is shown in figure 9(a). Also shown for reference, with dashed lines, are the fluxes of the inviscid theory (5.8). Reasonable quantitative agreement is found for all experiments, although for the wider channels there is little difference between the viscous and inviscid theories and it could be argued that both fit the data equally well. This is because the small aspect ratios in these cases mean that the depth-averaged velocity profiles only differ in thin boundary layers that do not significantly contribute to the overall flux. The difference is more pronounced in narrower channels with larger aspect ratios, since the viscous velocity profiles begin to diverge from the inviscid theory, and for a channel of width
![]() $W=15$
mm, angle
$W=15$
mm, angle
![]() ${\it\zeta}=26^{\circ }$
, the new equations represent a significant improvement on the inviscid case. This is highlighted in figure 9(b), which shows the same data on a log–log scale. For wider chutes the data roughly assumes a power-law relationship, with the
${\it\zeta}=26^{\circ }$
, the new equations represent a significant improvement on the inviscid case. This is highlighted in figure 9(b), which shows the same data on a log–log scale. For wider chutes the data roughly assumes a power-law relationship, with the
![]() $5/2$
gradient following from the analytic inviscid expression (5.8), whereas the narrower channels curve away from this relationship.
$5/2$
gradient following from the analytic inviscid expression (5.8), whereas the narrower channels curve away from this relationship.

Figure 9. (a) Plots of mass flux
![]() $M$
(in kg s
$M$
(in kg s
![]() $^{-1}$
) through the channel against flow thickness
$^{-1}$
) through the channel against flow thickness
![]() $h_{0}$
for different channel widths
$h_{0}$
for different channel widths
![]() $W$
and slope angles
$W$
and slope angles
![]() ${\it\zeta}$
. Solid lines denote theoretical predictions given by (5.6) and (5.7), where the velocity fields are solved assuming slip boundary conditions (4.14), (4.15) with wall-friction angle
${\it\zeta}$
. Solid lines denote theoretical predictions given by (5.6) and (5.7), where the velocity fields are solved assuming slip boundary conditions (4.14), (4.15) with wall-friction angle
![]() ${\it\zeta}_{w}=10^{\circ }$
. Dashed lines represent the inviscid theory (5.8). (b) The same data on a log–log scale.
${\it\zeta}_{w}=10^{\circ }$
. Dashed lines represent the inviscid theory (5.8). (b) The same data on a log–log scale.
It is worth noting that, whilst figure 9 and the theoretical expressions plot
![]() $M$
as a function of
$M$
as a function of
![]() $h_{0}$
, the data could equally have been presented the other way round since neither quantity is explicitly imposed in the experiments. Instead, the gate height is controlled and the flow thins to a constant thickness as it leaves the hopper. This gate height also sets the mass flux through the channel, so some readers may find it more natural to invert the relationships shown in figure 9.
$h_{0}$
, the data could equally have been presented the other way round since neither quantity is explicitly imposed in the experiments. Instead, the gate height is controlled and the flow thins to a constant thickness as it leaves the hopper. This gate height also sets the mass flux through the channel, so some readers may find it more natural to invert the relationships shown in figure 9.
In addition to the laser profilometer and balance data, a high-speed camera takes images of a 5 mm transverse slice of the chute at a rate of 2000 f.p.s. Using the open source software PIVlab for MATLAB (Thielicke & Stamhuis Reference Thielicke and Stamhuis2014), these images are used to calculate the surface velocity profiles
![]() $u_{s}(y)$
, which are averaged in time and downslope position. These are compared to the depth-averaged theory (5.9) and full rheology for two different channel widths and flow thicknesses and the results are shown in figures 10 and 11. Both sets of computations are calculated for slip boundary conditions with a wall-friction angle
$u_{s}(y)$
, which are averaged in time and downslope position. These are compared to the depth-averaged theory (5.9) and full rheology for two different channel widths and flow thicknesses and the results are shown in figures 10 and 11. Both sets of computations are calculated for slip boundary conditions with a wall-friction angle
![]() ${\it\zeta}_{w}=10^{\circ }$
, which is close to that used by Jop et al. (Reference Jop, Forterre and Pouliquen2005) for glass beads sliding on glass walls. For the wider channel (
${\it\zeta}_{w}=10^{\circ }$
, which is close to that used by Jop et al. (Reference Jop, Forterre and Pouliquen2005) for glass beads sliding on glass walls. For the wider channel (
![]() ${\it\varepsilon}=0.0455$
), the experimental data shows a central region of near-constant velocity, with a reasonably rapid decrease to zero near the flow boundaries. This is quantitatively captured by the depth-averaged theory, which fits the data as well as, if not better than, the full rheology (figure 10). Note that this behaviour is the opposite to what was found by Jop et al. (Reference Jop, Forterre and Pouliquen2005), where the sidewalls were shown to have a significant effect on the whole flow, even in the widest channels. However, their experiments involved particles moving over a thick erodible base, and the aspect ratios of the flowing layers were typically much larger than the flows considered here. One should therefore be cautious when drawing comparisons between such heap flows and the chute flows presented in this work.
${\it\varepsilon}=0.0455$
), the experimental data shows a central region of near-constant velocity, with a reasonably rapid decrease to zero near the flow boundaries. This is quantitatively captured by the depth-averaged theory, which fits the data as well as, if not better than, the full rheology (figure 10). Note that this behaviour is the opposite to what was found by Jop et al. (Reference Jop, Forterre and Pouliquen2005), where the sidewalls were shown to have a significant effect on the whole flow, even in the widest channels. However, their experiments involved particles moving over a thick erodible base, and the aspect ratios of the flowing layers were typically much larger than the flows considered here. One should therefore be cautious when drawing comparisons between such heap flows and the chute flows presented in this work.
The results are not as promising for a narrower geometry (
![]() ${\it\varepsilon}=0.201$
, figure 11). The mean magnitudes from the PIV agree with the depth-averaged theory but the shape of the surface velocity profiles are significantly different. In particular, the depth-averaged theory predicts that the velocity approaches zero at the sidewalls, whereas the experiments suggest a notable slip velocity that is indeed captured in the full rheology solutions. This suggests that the Bagnold profile (5.3) used to reconstruct the surface velocities may not be appropriate for narrower channels, especially near the lateral boundaries. Nevertheless, in all cases there is a curvature profile across the channel width and the viscous depth-averaged equations go some way to model this, representing a significant improvement on classical hyperbolic theory.
${\it\varepsilon}=0.201$
, figure 11). The mean magnitudes from the PIV agree with the depth-averaged theory but the shape of the surface velocity profiles are significantly different. In particular, the depth-averaged theory predicts that the velocity approaches zero at the sidewalls, whereas the experiments suggest a notable slip velocity that is indeed captured in the full rheology solutions. This suggests that the Bagnold profile (5.3) used to reconstruct the surface velocities may not be appropriate for narrower channels, especially near the lateral boundaries. Nevertheless, in all cases there is a curvature profile across the channel width and the viscous depth-averaged equations go some way to model this, representing a significant improvement on classical hyperbolic theory.

Figure 10. Surface velocity measurements
![]() $\hat{u} _{s}({\hat{y}})$
for a wide channel of width
$\hat{u} _{s}({\hat{y}})$
for a wide channel of width
![]() $W=100$
mm, height
$W=100$
mm, height
![]() $h_{0}=4.55$
mm (giving aspect ratio
$h_{0}=4.55$
mm (giving aspect ratio
![]() ${\it\varepsilon}=0.0455$
) and angle
${\it\varepsilon}=0.0455$
) and angle
![]() ${\it\zeta}=26^{\circ }$
(crosses). Solid lines denote the new depth-averaged theory (5.9) and the dashed lines are the solutions of the full rheology. Both computations are calculated with slip boundary conditions and a wall-friction angle
${\it\zeta}=26^{\circ }$
(crosses). Solid lines denote the new depth-averaged theory (5.9) and the dashed lines are the solutions of the full rheology. Both computations are calculated with slip boundary conditions and a wall-friction angle
![]() ${\it\zeta}_{w}=10^{\circ }$
. The dash-dotted lines show the depth-averaged profiles when a reduced wall-friction angle
${\it\zeta}_{w}=10^{\circ }$
. The dash-dotted lines show the depth-averaged profiles when a reduced wall-friction angle
![]() ${\it\zeta}_{w}=3.3^{\circ }$
is used.
${\it\zeta}_{w}=3.3^{\circ }$
is used.

Figure 11. Surface velocity measurements
![]() $\hat{u} _{s}({\hat{y}})$
for a narrow channel of width
$\hat{u} _{s}({\hat{y}})$
for a narrow channel of width
![]() $W=15$
mm, height
$W=15$
mm, height
![]() $h_{0}=3.01$
mm (giving aspect ratio
$h_{0}=3.01$
mm (giving aspect ratio
![]() ${\it\varepsilon}=0.201$
) and angle
${\it\varepsilon}=0.201$
) and angle
![]() ${\it\zeta}=28^{\circ }$
(crosses). Solid lines denote the new depth-averaged theory (5.9) and the dashed lines are the solutions of the full rheology. Both computations are calculated with slip boundary conditions and a wall-friction angle
${\it\zeta}=28^{\circ }$
(crosses). Solid lines denote the new depth-averaged theory (5.9) and the dashed lines are the solutions of the full rheology. Both computations are calculated with slip boundary conditions and a wall-friction angle
![]() ${\it\zeta}_{w}=10^{\circ }$
. The dash-dotted lines show the depth-averaged profiles when a reduced wall-friction angle
${\it\zeta}_{w}=10^{\circ }$
. The dash-dotted lines show the depth-averaged profiles when a reduced wall-friction angle
![]() ${\it\zeta}_{w}=3.3^{\circ }$
is used.
${\it\zeta}_{w}=3.3^{\circ }$
is used.
Note that it is possible to reduce the wall-friction angle
![]() ${\it\zeta}_{w}$
so that the depth-averaged surface velocities are in better agreement for the narrower channel in figure 11. Decreasing
${\it\zeta}_{w}$
so that the depth-averaged surface velocities are in better agreement for the narrower channel in figure 11. Decreasing
![]() ${\it\zeta}_{w}$
to
${\it\zeta}_{w}$
to
![]() $3.3^{\circ }$
leads to greater slip velocities at the walls and a significantly improved fit, as shown by the dash-dotted line in figure 11. However, a corresponding reduction in the sidewall friction in the full
$3.3^{\circ }$
leads to greater slip velocities at the walls and a significantly improved fit, as shown by the dash-dotted line in figure 11. However, a corresponding reduction in the sidewall friction in the full
![]() ${\it\mu}(I)$
-rheology increases the surface velocity and flattens the cross-slope profile (not shown), so in this case the fit is not as good as that achieved with the higher
${\it\mu}(I)$
-rheology increases the surface velocity and flattens the cross-slope profile (not shown), so in this case the fit is not as good as that achieved with the higher
![]() ${\it\zeta}_{w}=10^{\circ }$
. In both theories, imposing Coulomb friction at the walls essentially amounts to specifying the velocity gradients there, and since the transverse structure of the flow is different the apparent wall friction needed to achieve a good fit will also differ. Figure 11 highlights the uncertainties regarding what happens at the lateral boundaries, and suggests that including a velocity dependent wall-friction coefficient may be necessary to unify the theories.
${\it\zeta}_{w}=10^{\circ }$
. In both theories, imposing Coulomb friction at the walls essentially amounts to specifying the velocity gradients there, and since the transverse structure of the flow is different the apparent wall friction needed to achieve a good fit will also differ. Figure 11 highlights the uncertainties regarding what happens at the lateral boundaries, and suggests that including a velocity dependent wall-friction coefficient may be necessary to unify the theories.
It is expected, however, that some of the discrepancies between the two theories will not be completely removed by implementing more complicated wall-friction laws. In particular, the different transverse structure in the solutions appears to be a robust feature. This difference may be partially explained by considering the relevant steps in the derivation of each model. The depth-averaged equations are based on the assumption that the basal friction coefficient is given by (2.5), a law that is derived for steady flows uniform in both the downslope and cross-slope directions. Consequently, transverse velocity gradients are not taken into consideration. Whilst it has been shown that the law is able to accurately model granular flow configurations outside of the initial remit (e.g. Pouliquen Reference Pouliquen1999b
), these transverse gradients are particularly significant in narrow channels, and so (2.5) may not be strictly valid here. The full
![]() ${\it\mu}(I)$
-rheology, on the other hand, uses the inertial number
${\it\mu}(I)$
-rheology, on the other hand, uses the inertial number
![]() $I$
defined by (2.12), to include the effect of cross-slope velocity gradients. The viscous terms in the depth-averaged equations are closely related to this rheology but only in the steady uniform regime where cross-slope derivatives are once again neglected.
$I$
defined by (2.12), to include the effect of cross-slope velocity gradients. The viscous terms in the depth-averaged equations are closely related to this rheology but only in the steady uniform regime where cross-slope derivatives are once again neglected.
As a final note, figures 9–11 show how varying the channel width affects the mass flux and surface velocity profiles, with the lateral sidewalls becoming more significant in narrower channels. This behaviour was also noticed during laboratory experiments. Slopes angles and gate heights that gave rise to steady uniform flows for wide chutes produced decelerating flows or even no flow at all as the channel width was decreased, meaning the frictional walls play an important role on the flow characteristics.
8. Discussion and conclusions
This paper presents a two-dimensional depth-averaged
![]() ${\it\mu}(I)$
-rheology for shallow granular free-surface flows. It generalizes the one-dimensional version (Gray & Edwards Reference Gray and Edwards2014) in a natural manner, ensuring the resulting tensor constitutive law is frame-invariant in a two-dimensional depth-averaged framework. In their most general form, the governing equations have the potential to model several different granular flow phenomena and geometries. Here, they are solved for the test case of a steady flow between two parallel plates. Previous two-dimensional inviscid models give constant velocity profiles across the channel width, whereas the new equations admit more realistic curved solutions that account for wall-friction effects. By scaling the cross-slope coordinate on the width of the channel and the downslope velocity on the one-dimensional steady uniform solution, a one-dimensional ODE (4.17) together with no-slip (4.19) and slip boundary conditions (4.20), (4.21) are formulated which are independent of scale. The only controlling parameters are the channel aspect ratio, the slope inclination and the frictional properties of the grains and the chute.
${\it\mu}(I)$
-rheology for shallow granular free-surface flows. It generalizes the one-dimensional version (Gray & Edwards Reference Gray and Edwards2014) in a natural manner, ensuring the resulting tensor constitutive law is frame-invariant in a two-dimensional depth-averaged framework. In their most general form, the governing equations have the potential to model several different granular flow phenomena and geometries. Here, they are solved for the test case of a steady flow between two parallel plates. Previous two-dimensional inviscid models give constant velocity profiles across the channel width, whereas the new equations admit more realistic curved solutions that account for wall-friction effects. By scaling the cross-slope coordinate on the width of the channel and the downslope velocity on the one-dimensional steady uniform solution, a one-dimensional ODE (4.17) together with no-slip (4.19) and slip boundary conditions (4.20), (4.21) are formulated which are independent of scale. The only controlling parameters are the channel aspect ratio, the slope inclination and the frictional properties of the grains and the chute.
The solutions tend to the inviscid value in the small aspect ratio limit (wide channels), with boundary layers forming at the sidewalls, while for large aspect ratio (narrow) channels the profiles are parabolic in nature with near-constant curvature, as shown in figure 2. Figure 3 shows how the profiles change for different wall-friction angles. If the walls are frictionless the inviscid solution is recovered. However, as the friction angle increases, the wall slip velocity is reduced, and is equal to zero at a critical wall-friction angle
![]() ${\it\zeta}_{w}^{\ast }$
. Above this value, the concavity of the ODE and sign functions of the velocity in the boundary conditions prevent negative slip and, interestingly, lead to solutions that are equivalent to applying no-slip boundary conditions, as shown in the inset plot in figure 3.
${\it\zeta}_{w}^{\ast }$
. Above this value, the concavity of the ODE and sign functions of the velocity in the boundary conditions prevent negative slip and, interestingly, lead to solutions that are equivalent to applying no-slip boundary conditions, as shown in the inset plot in figure 3.
When the Bagnold solution for one-dimensional steady uniform flows is used to reconstruct the downslope velocity profiles with depth, reasonable quantitative agreement is found with solutions of the full
![]() ${\it\mu}(I)$
-rheology for both wide and narrow channels, although the agreement is significantly better in the former. This provides justification for the simplifying assumptions, allowing more straightforward equations to be used to obtain similar results in this geometry. Note that when made non-dimensional appropriately the PDE for the full
${\it\mu}(I)$
-rheology for both wide and narrow channels, although the agreement is significantly better in the former. This provides justification for the simplifying assumptions, allowing more straightforward equations to be used to obtain similar results in this geometry. Note that when made non-dimensional appropriately the PDE for the full
![]() ${\it\mu}(I)$
-rheology (6.24) together with either no-slip (6.28) or slip boundary conditions (6.29), (6.30), are also scale invariant, which is an interesting parallel to the depth-averaged case.
${\it\mu}(I)$
-rheology (6.24) together with either no-slip (6.28) or slip boundary conditions (6.29), (6.30), are also scale invariant, which is an interesting parallel to the depth-averaged case.
The relationship between flow thickness and mass flux is investigated for a range of channel widths and slope angles, and good agreement is found between experimental data and the depth-averaged theory. For wide chutes, the difference between viscous and inviscid curves is sufficiently small to argue that both fit the experimental data equally well. However, the two curves begin to diverge in narrow chutes as the flow thickness increases and wall effects play a significant role. In this case, the reduced fluxes of the depth-averaged viscous model are noticeably closer to the measured values.
A similar improvement in the flux-thickness curves could be made by using width-averaged models (e.g. Greve & Hutter Reference Greve and Hutter1993; Taberlet et al. Reference Taberlet, Richard, Valance, Losert, Pasini, Jenkins and Delannay2003) to capture the increased wall-friction effects in narrow chutes. However, the specific details of the velocity profiles in the transverse direction are lost during the width-averaging process, and so these models can only predict a constant value for the velocity. The new viscous theory, however, admits more realistic curved solutions and therefore represents a significant improvement. This is confirmed using PIV to measure the surface velocity profiles for channels with different aspect ratios. In all cases there is clear lateral variation, providing justification for including the additional viscous terms that give rise to these profiles. The agreement between experiments and depth-averaged theory is much better for wider channels, which is consistent with the shallowness assumption used in deriving the governing equations.
Acknowledgements
This research was supported by NERC grants NE/E003206/1 and NE/K003011/1 as well as EPSRC grants EP/I019189/1, EP/K00428X/1 and EP/M022447/1. J.L.B. would also like to acknowledge support from a NERC doctoral training award.