1. Introduction
Liquid can break up or fragment in multiphase turbulence (Deane & Stokes Reference Deane and Stokes2002; Villermaux Reference Villermaux2007; Wang, Mathai & Sun Reference Wang, Mathai and Sun2019; Villermaux Reference Villermaux2020). This physical phenomenon is very important for raindrops (Josserand & Zaleski Reference Josserand and Zaleski2003; Villermaux & Bossa Reference Villermaux and Bossa2009), for ocean waves and the resulting spray (Veron Reference Veron2015), and even for the transmission of virus-laden droplets during coughing or sneezing (Bourouiba Reference Bourouiba2020; Chong et al. Reference Chong, Ng, Hori, Yang, Verzicco and Lohse2021). Once the physical mechanisms governing this important phenomenon are understood, one can deduce quantitative criteria for the breakup to occur. In turbulence, for drops or bubbles, the breakup criteria can be deduced from the balance of inertial and surface tension forces, as developed in the Kolmogorov–Hinze theory (Kolmogorov Reference Kolmogorov1949; Hinze Reference Hinze1955). This theory well predicts the breakup criteria in experimental and numerical results in various flow systems, e.g. homogeneous isotropic turbulence (Martínez-Bazán, Montañés & Lasheras Reference Martínez-Bazán, Montañés and Lasheras1999; Perlekar et al. Reference Perlekar, Biferale, Sbragaglia, Srivastava and Toschi2012; MuKolmogorov-Hinzeerjee et al. Reference MuKolmogorov-Hinzeerjee, Safdari, Shardt, Kenjereš and Van den Akker2019), shear flows (Rosti et al. Reference Rosti, Ge, Jain, Dodd and Brandt2019), pipe flows (Hesketh, Etchells & Russell Reference Hesketh, Etchells and Russell1991) and ocean waves (Deane & Stokes Reference Deane and Stokes2002; Deike, Melville & Popinet Reference Deike, Melville and Popinet2016).
While the classical Kolmogorov–Hinze theory considers only surface tension and inertial forces, in many multiphase turbulent flows also buoyancy can play an important role. Examples of multiphase buoyant turbulence include the hotspots and superswells in the Earth's mantle (Davaille Reference Davaille1999; Tackley Reference Tackley2000) and even flows during sneezing and exhalation (Bourouiba, Dehandschoewercker & Bush Reference Bourouiba, Dehandschoewercker and Bush2014). In such flows, the breakup of the interface between the fluids is the key phenomenon. Yet, the exact mechanisms that drive interface breakup when buoyancy is crucial are unknown.
The objective of the present work is to shed light on these mechanisms. As examples for turbulent flow where buoyancy is important and at the same time can easily be tuned, we take thermal convection, namely Rayleigh–Bénard (RB) convection (Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009; Lohse & Xia Reference Lohse and Xia2010; Chillà & Schumacher Reference Chillà and Schumacher2012) of two immiscible fluids. We numerically investigate the breakup mechanisms of the interface between the two immiscible fluids. The immiscible fluids are first arranged in two layers according to their densities and then heated from below and cooled from above. Most previous studies of such two-layer RB convection were conducted in the non-turbulent regime (Nataf, Moreno & Cardin Reference Nataf, Moreno and Cardin1988; Prakash & Koster Reference Prakash and Koster1994; Busse & Petry Reference Busse and Petry2009; Diwakar et al. Reference Diwakar, Tiwari, Das and Sundararajan2014). Experimental studies in the turbulent regime were reported by Xie & Xia (Reference Xie and Xia2013), who focused on the flow structures in each layer and the coupling modes between the flows in the two layers, including viscous coupling and thermal coupling. Besides the classical rectangular/cylindrical configuration, the two-layer RB convection in spherical-shell geometry was also numerically studied by Yoshida & Hamano (Reference Yoshida and Hamano2016). However, these previous studies only considered the case for strong surface tension, where the interface between the layers does not break up. In this study, we will for the first time explore the case with interface breakup, which happens when surface tension is sufficiently small.
The control parameters of two-layer RB convection are the density ratio ![]() $\varLambda$ between two fluids and the Weber number
$\varLambda$ between two fluids and the Weber number ![]() $We$, which is the ratio of inertia to surface tension. We will keep the Prandtl number
$We$, which is the ratio of inertia to surface tension. We will keep the Prandtl number ![]() $Pr$ (a material property) and the Rayleigh number
$Pr$ (a material property) and the Rayleigh number ![]() $Ra$ (the dimensionless temperature difference between the plates) fixed, at values allowing for considerable turbulence. Our main result will be the phase diagram in the parameter space (
$Ra$ (the dimensionless temperature difference between the plates) fixed, at values allowing for considerable turbulence. Our main result will be the phase diagram in the parameter space (![]() $We, \varLambda$), in which we identify the non-breakup and breakup regimes. At increasing
$We, \varLambda$), in which we identify the non-breakup and breakup regimes. At increasing ![]() $We$, we observe two distinct types of interface breakup. At small
$We$, we observe two distinct types of interface breakup. At small ![]() $\varLambda \ll 1$, the mechanism is well-described by the Kolmogorov–Hinze theory. However, at large
$\varLambda \ll 1$, the mechanism is well-described by the Kolmogorov–Hinze theory. However, at large ![]() $0.5<\varLambda \leqslant 1$, the breakup is dominated by a balance between buoyancy and surface tension forces, leading to a periodic overturning-type breakup.
$0.5<\varLambda \leqslant 1$, the breakup is dominated by a balance between buoyancy and surface tension forces, leading to a periodic overturning-type breakup.
The organization of this paper is as follows. The numerical methodology is introduced in § 2. Then in § 3, we validate our code by studying droplet fragmentation in thermal turbulence and favourably compare the results to the Kolmogorov–Hinze theory. The main results on the interface breakup in two-layer RB turbulence are presented in § 4, including a discussion of the first and second types of interface breakup in §§ 4.1 and 4.2, respectively, and the analysis of the critical Weber number for interface breakup in § 4.3. We finalize and further discuss our findings in § 5.
2. Methodology: Cahn–Hilliard approach coupled to finite difference scheme
In this study, we performed the simulations in a two-dimensional (2-D) rectangular domain with aspect ratio ![]() $\varGamma =2$ (width divided by height). Although 2-D RB convection is different from a three-dimensional (3-D) one, it still captures many essential features thereof (van der Poel, Stevens & Lohse Reference van der Poel, Stevens and Lohse2013). The direct numerical simulations solver for the Navier–Stokes equations is a second-order finite-difference open source solver (Verzicco & Orlandi Reference Verzicco and Orlandi1996; van der Poel et al. Reference van der Poel, Ostilla-Mónico, Donners and Verzicco2015), namely AFiD, which has been well validated and used to study various turbulent flows (Stevens et al. Reference Stevens, Blass, Zhu, Verzicco and Lohse2018; Zhu et al. Reference Zhu, Verschoof, BaKolmogorov-Hinzeuis, Huisman, Verzicco, Sun and Lohse2018b; Blass et al. Reference Blass, Zhu, Verzicco, Lohse and Stevens2020; Wang et al. Reference Wang, Chong, Stevens, Verzicco and Lohse2020Reference Wang, Verzicco, Lohse and Shishkinaa,b). To simulate multiphase turbulent flows, we combine AFiD with the phase-field method (Jacqmin Reference Jacqmin1999; Ding, Spelt & Shu Reference Ding, Spelt and Shu2007; Liu & Ding Reference Liu and Ding2015), which has also been successfully applied to the interfacial (Zhu et al. Reference Zhu, Liu, Mu, Gao and Ding2017; Chen et al. Reference Chen, Liu, Lu and Ding2018; Liu et al. Reference Liu, Zhang, Gao, Lu and Ding2018; Chen et al. Reference Chen, Liu, Gao and Ding2020) and turbulent flows (Roccon, Zonta & Soldati Reference Roccon, Zonta and Soldati2019; Soligo, Roccon & Soldati Reference Soligo, Roccon and Soldati2019a).
$\varGamma =2$ (width divided by height). Although 2-D RB convection is different from a three-dimensional (3-D) one, it still captures many essential features thereof (van der Poel, Stevens & Lohse Reference van der Poel, Stevens and Lohse2013). The direct numerical simulations solver for the Navier–Stokes equations is a second-order finite-difference open source solver (Verzicco & Orlandi Reference Verzicco and Orlandi1996; van der Poel et al. Reference van der Poel, Ostilla-Mónico, Donners and Verzicco2015), namely AFiD, which has been well validated and used to study various turbulent flows (Stevens et al. Reference Stevens, Blass, Zhu, Verzicco and Lohse2018; Zhu et al. Reference Zhu, Verschoof, BaKolmogorov-Hinzeuis, Huisman, Verzicco, Sun and Lohse2018b; Blass et al. Reference Blass, Zhu, Verzicco, Lohse and Stevens2020; Wang et al. Reference Wang, Chong, Stevens, Verzicco and Lohse2020Reference Wang, Verzicco, Lohse and Shishkinaa,b). To simulate multiphase turbulent flows, we combine AFiD with the phase-field method (Jacqmin Reference Jacqmin1999; Ding, Spelt & Shu Reference Ding, Spelt and Shu2007; Liu & Ding Reference Liu and Ding2015), which has also been successfully applied to the interfacial (Zhu et al. Reference Zhu, Liu, Mu, Gao and Ding2017; Chen et al. Reference Chen, Liu, Lu and Ding2018; Liu et al. Reference Liu, Zhang, Gao, Lu and Ding2018; Chen et al. Reference Chen, Liu, Gao and Ding2020) and turbulent flows (Roccon, Zonta & Soldati Reference Roccon, Zonta and Soldati2019; Soligo, Roccon & Soldati Reference Soligo, Roccon and Soldati2019a).
We consider two immiscible fluid layers of the same volume placed in the domain, named fluid ![]() $H$ for the heavier fluid initially at the bottom and fluid
$H$ for the heavier fluid initially at the bottom and fluid ![]() $L$ for the lighter fluid initially at the top. The mathematically sharp interface between two fluids is modelled by a diffuse interface with finite thickness, and can be represented by contours of the volume fraction
$L$ for the lighter fluid initially at the top. The mathematically sharp interface between two fluids is modelled by a diffuse interface with finite thickness, and can be represented by contours of the volume fraction ![]() $C$ of fluid
$C$ of fluid ![]() $H$. The corresponding volume fraction of fluid
$H$. The corresponding volume fraction of fluid ![]() $L$ is
$L$ is ![]() $1-C$. The evolution of
$1-C$. The evolution of ![]() $C$ is governed by the Cahn–Hilliard equations,
$C$ is governed by the Cahn–Hilliard equations,
where ![]() $\boldsymbol {u}$ is the flow velocity, and
$\boldsymbol {u}$ is the flow velocity, and ![]() $\psi = C^{3} - 1.5 C^{2}+ 0.5 C -{Cn}^{2} \nabla ^2 C$ is the chemical potential. The Cahn number
$\psi = C^{3} - 1.5 C^{2}+ 0.5 C -{Cn}^{2} \nabla ^2 C$ is the chemical potential. The Cahn number ![]() ${Cn}=0.75h/D$, where
${Cn}=0.75h/D$, where ![]() $h$ is the mesh size and
$h$ is the mesh size and ![]() $D$ the domain height, and the Péclet number
$D$ the domain height, and the Péclet number ![]() $Pe=0.9/{Cn}$ are set the same as in Liu, Gao & Ding (Reference Liu, Gao and Ding2017) and Li, Liu & Ding (Reference Li, Liu and Ding2020). To overcome the mass loss in the phase-field method, a correction method as proposed by Wang et al. (Reference Wang, Shu, Shao, Wu and Niu2015) is used. This correction method resembles that used in Soligo, Roccon & Soldati (Reference Soligo, Roccon and Soldati2019b) and exhibits good performance (see § 3).
$Pe=0.9/{Cn}$ are set the same as in Liu, Gao & Ding (Reference Liu, Gao and Ding2017) and Li, Liu & Ding (Reference Li, Liu and Ding2020). To overcome the mass loss in the phase-field method, a correction method as proposed by Wang et al. (Reference Wang, Shu, Shao, Wu and Niu2015) is used. This correction method resembles that used in Soligo, Roccon & Soldati (Reference Soligo, Roccon and Soldati2019b) and exhibits good performance (see § 3).
The motion of the fluids is governed by the Navier–Stokes equation, heat transfer equation and continuity,
here given in non-dimensionalized form. We have used the material properties of fluid ![]() $H$, the domain height
$H$, the domain height ![]() $D$, the temperature difference
$D$, the temperature difference ![]() $\varDelta$ between plates, and the free-fall velocity
$\varDelta$ between plates, and the free-fall velocity ![]() $U=\sqrt {\alpha g D \varDelta }$ to make these equations dimensionless, where
$U=\sqrt {\alpha g D \varDelta }$ to make these equations dimensionless, where ![]() $\alpha$ is the thermal expansion coefficient of fluid
$\alpha$ is the thermal expansion coefficient of fluid ![]() $H$ and
$H$ and ![]() $g$ the gravitational acceleration. Then we define
$g$ the gravitational acceleration. Then we define ![]() $\rho =C+\varLambda (1-C)$ as the dimensionless density,
$\rho =C+\varLambda (1-C)$ as the dimensionless density, ![]() $P$ the dimensionless pressure,
$P$ the dimensionless pressure, ![]() $\mu$ the dimensionless dynamic viscosity,
$\mu$ the dimensionless dynamic viscosity, ![]() $C_p$ the dimensionless specific heat capacity,
$C_p$ the dimensionless specific heat capacity, ![]() $k$ the dimensionless thermal conductivity,
$k$ the dimensionless thermal conductivity, ![]() ${\boldsymbol {F}}_{st}=6\sqrt {2}\psi \boldsymbol {\nabla } C / ({Cn\,We})$ the dimensionless surface tension force,
${\boldsymbol {F}}_{st}=6\sqrt {2}\psi \boldsymbol {\nabla } C / ({Cn\,We})$ the dimensionless surface tension force, ![]() $\theta$ the dimensionless temperature,
$\theta$ the dimensionless temperature, ![]() $\boldsymbol {j}$ the unit vector in vertical direction. The superscript
$\boldsymbol {j}$ the unit vector in vertical direction. The superscript ![]() $T$ stands for the transpose. Note that
$T$ stands for the transpose. Note that ![]() $\rho$,
$\rho$, ![]() $\mu$,
$\mu$, ![]() $C_p$ and
$C_p$ and ![]() $k$ in general vary in space.
$k$ in general vary in space.
In thermal flows, the density also depends on the temperature, so the dimensional density is defined as ![]() $\hat {\rho }=\hat {\rho }_H(T)C+\hat {\rho }_L(T)(1-C)$, where the subscripts
$\hat {\rho }=\hat {\rho }_H(T)C+\hat {\rho }_L(T)(1-C)$, where the subscripts ![]() $H$ and
$H$ and ![]() $L$ represent fluid
$L$ represent fluid ![]() $H$ and fluid
$H$ and fluid ![]() $L$, respectively, and
$L$, respectively, and ![]() $\hat {\rho }_i(T)=[1-\alpha (T-T_c)]\hat {\rho }_i(T_c)$ with
$\hat {\rho }_i(T)=[1-\alpha (T-T_c)]\hat {\rho }_i(T_c)$ with ![]() $T_c$ being the temperature on the top cold plate. Then we rewrite the dimensional density as
$T_c$ being the temperature on the top cold plate. Then we rewrite the dimensional density as ![]() $\hat {\rho }=[\rho -\alpha (T-T_c)\rho ]\hat {\rho }_H(T_c)$. Further considering the Oberbeck–Boussinesq approximation in the Navier–Stokes equation (2.2), we have the dimensionless density
$\hat {\rho }=[\rho -\alpha (T-T_c)\rho ]\hat {\rho }_H(T_c)$. Further considering the Oberbeck–Boussinesq approximation in the Navier–Stokes equation (2.2), we have the dimensionless density ![]() $\rho$ in the inertia term,
$\rho$ in the inertia term, ![]() $\rho \theta$, as the buoyancy term, and
$\rho \theta$, as the buoyancy term, and ![]() $\rho /Fr$ as the gravity term, which cannot be ignored as in the single phase simulation, due to the different densities of the fluids. Furthermore, we only consider the case without phase transition.
$\rho /Fr$ as the gravity term, which cannot be ignored as in the single phase simulation, due to the different densities of the fluids. Furthermore, we only consider the case without phase transition.
The properties of fluid ![]() $H$ and fluid
$H$ and fluid ![]() $L$ are set as follows: their density ratio is
$L$ are set as follows: their density ratio is ![]() $\varLambda =\rho _L/\rho _H \leqslant 1$. Except for the density
$\varLambda =\rho _L/\rho _H \leqslant 1$. Except for the density ![]() $\rho$, all other properties of the two fluids are the same. The other dimensionless parameters are
$\rho$, all other properties of the two fluids are the same. The other dimensionless parameters are ![]() $We=\rho _H U^2 D/\sigma$,
$We=\rho _H U^2 D/\sigma$, ![]() $Ra=\alpha g D^3 \varDelta /(\nu \kappa )$,
$Ra=\alpha g D^3 \varDelta /(\nu \kappa )$, ![]() $Pr=\nu /\kappa$, the Froude number
$Pr=\nu /\kappa$, the Froude number ![]() $Fr=U^2/(gD)$ (the ratio of inertia to gravity). Here
$Fr=U^2/(gD)$ (the ratio of inertia to gravity). Here ![]() $\sigma$ is the surface tension coefficient,
$\sigma$ is the surface tension coefficient, ![]() $\nu =\mu /\rho$ the kinematic viscosity, and
$\nu =\mu /\rho$ the kinematic viscosity, and ![]() $\kappa =k/(\rho C_p)$ the thermal diffusivity. We fix
$\kappa =k/(\rho C_p)$ the thermal diffusivity. We fix ![]() $Ra=10^8$,
$Ra=10^8$, ![]() $Pr=1$,
$Pr=1$, ![]() $Fr=1$ and
$Fr=1$ and ![]() $\varGamma =2$ (these values chosen to both ensure flows in the turbulent regime and simplify the simulations), and only vary
$\varGamma =2$ (these values chosen to both ensure flows in the turbulent regime and simplify the simulations), and only vary ![]() $We$ from
$We$ from ![]() $5$ to
$5$ to ![]() $5000$ and
$5000$ and ![]() $\varLambda$ from
$\varLambda$ from ![]() $0.001$ (e.g. air–water system) to
$0.001$ (e.g. air–water system) to ![]() $1$ (e.g. oil–water system).
$1$ (e.g. oil–water system).
The boundary conditions at the top and bottom plates are set as ![]() $\partial C/\partial {\boldsymbol {j}}=0$,
$\partial C/\partial {\boldsymbol {j}}=0$, ![]() ${\boldsymbol {j}}\boldsymbol {\cdot }\boldsymbol {\nabla } \psi =0$, no-slip velocities and fixed temperature
${\boldsymbol {j}}\boldsymbol {\cdot }\boldsymbol {\nabla } \psi =0$, no-slip velocities and fixed temperature ![]() $\theta =0$ (top) and
$\theta =0$ (top) and ![]() $1$ (bottom). Periodic conditions are used in the horizontal direction. All the simulations begin with the same initial velocity and temperature fields, which originate from a well-developed turbulent flow at
$1$ (bottom). Periodic conditions are used in the horizontal direction. All the simulations begin with the same initial velocity and temperature fields, which originate from a well-developed turbulent flow at ![]() $We=5$ and
$We=5$ and ![]() $\varLambda =1$. Uniform grids with
$\varLambda =1$. Uniform grids with ![]() $1000 \times 500$ gridpoints are used, which are sufficient for
$1000 \times 500$ gridpoints are used, which are sufficient for ![]() $Ra=10^8$ and
$Ra=10^8$ and ![]() $Pr=1$, consistent with the grid resolution checks in Zhang, Zhou & Sun (Reference Zhang, Zhou and Sun2017). The details of the discretizations can be found in Ding et al. (Reference Ding, Spelt and Shu2007), Verzicco & Orlandi (Reference Verzicco and Orlandi1996), and Dodd & Ferrante (Reference Dodd and Ferrante2014).
$Pr=1$, consistent with the grid resolution checks in Zhang, Zhou & Sun (Reference Zhang, Zhou and Sun2017). The details of the discretizations can be found in Ding et al. (Reference Ding, Spelt and Shu2007), Verzicco & Orlandi (Reference Verzicco and Orlandi1996), and Dodd & Ferrante (Reference Dodd and Ferrante2014).
3. Droplet fragmentation in turbulent flow
We have verified our code against the existing theory from the literature. In this section, RB convection with drops are simulated. Initially, the temperature field has a linear profile, the velocity field is set to ![]() $0$, and a big drop of fluid
$0$, and a big drop of fluid ![]() $H$ with a diameter of
$H$ with a diameter of ![]() $0.5D$ is placed at the centre of the domain. The plates are superhydrophobic for fluid
$0.5D$ is placed at the centre of the domain. The plates are superhydrophobic for fluid ![]() $H$, i.e.
$H$, i.e. ![]() $C=0$ is used on both plates in the verification cases. We set
$C=0$ is used on both plates in the verification cases. We set ![]() $\varLambda =1$ and
$\varLambda =1$ and ![]() $We$ from
$We$ from ![]() $2000$ to 16 000, and use uniform grids with
$2000$ to 16 000, and use uniform grids with ![]() $2000 \times 1000$ gridpoints. Note that the value of
$2000 \times 1000$ gridpoints. Note that the value of ![]() $We$ is large because it is a system Weber number, and the local Weber number of drops calculated from simulations is of the order of
$We$ is large because it is a system Weber number, and the local Weber number of drops calculated from simulations is of the order of ![]() $1$.
$1$.
From the snapshot with the advecting drops in figure 1, we observe the large-scale circulation, which is well known from single phase convection (Krishnamurti & Howard Reference Krishnamurti and Howard1981; Xi, Lam & Xia Reference Xi, Lam and Xia2004; Xie, Ding & Xia Reference Xie, Ding and Xia2018; Zhu et al. Reference Zhu, Mathai, Stevens, Verzicco and Lohse2018a). Figure 2(b) displays the distribution of the drop size ![]() $S$, which follows the scaling law
$S$, which follows the scaling law ![]() $(S/D)^{-10/3}$ (Garrett, Li & Farmer Reference Garrett, Li and Farmer2000; Yu, Hendrickson & Yue Reference Yu, Hendrickson and Yue2020) valid for large drops. This scaling is consistent with experimental and other numerical results where the breakup of waves (Deane & Stokes Reference Deane and Stokes2002; Deike et al. Reference Deike, Melville and Popinet2016) or of a big drop (MuKolmogorov-Hinzeerjee et al. Reference MuKolmogorov-Hinzeerjee, Safdari, Shardt, Kenjereš and Van den Akker2019) was studied. Moreover, the maximal size of drops
$(S/D)^{-10/3}$ (Garrett, Li & Farmer Reference Garrett, Li and Farmer2000; Yu, Hendrickson & Yue Reference Yu, Hendrickson and Yue2020) valid for large drops. This scaling is consistent with experimental and other numerical results where the breakup of waves (Deane & Stokes Reference Deane and Stokes2002; Deike et al. Reference Deike, Melville and Popinet2016) or of a big drop (MuKolmogorov-Hinzeerjee et al. Reference MuKolmogorov-Hinzeerjee, Safdari, Shardt, Kenjereš and Van den Akker2019) was studied. Moreover, the maximal size of drops ![]() $S_{max}$ (see figure 2c) well agrees with the Kolmogorov–Hinze scaling law
$S_{max}$ (see figure 2c) well agrees with the Kolmogorov–Hinze scaling law ![]() $S_{max}/D \sim We^{-3/5}$, which originates from Hinze (Reference Hinze1955),
$S_{max}/D \sim We^{-3/5}$, which originates from Hinze (Reference Hinze1955),
 \begin{equation} S_{Hinze} \sim \left(\frac{\sigma}{\rho}\right)^{3/5}\epsilon^{-{2/5}}, \end{equation}
\begin{equation} S_{Hinze} \sim \left(\frac{\sigma}{\rho}\right)^{3/5}\epsilon^{-{2/5}}, \end{equation}
where ![]() $S_{Hinze}$ is the Hinze length scale and
$S_{Hinze}$ is the Hinze length scale and ![]() $\epsilon$ the energy dissipation rate of the turbulent flow. In the Kolmogorov–Hinze theory, one assumption is that the local Weber number defined by the size and velocity of the drops adjusts such that it is
$\epsilon$ the energy dissipation rate of the turbulent flow. In the Kolmogorov–Hinze theory, one assumption is that the local Weber number defined by the size and velocity of the drops adjusts such that it is ![]() $We_{local} \sim O(1)$. Indeed, in our simulations, the local drop size adjusts correspondingly, so this assumption is fulfilled. The second assumption is that the flow exhibits inertial subrange scaling in the region of wavelengths comparable to the size of the largest drops. The spatial location where this assumption holds in RB convection is in the bulk region of convection (Lohse & Xia Reference Lohse and Xia2010). Therefore, the Kolmogorov–Hinze theory can indeed also be reasonably applied to 2-D RB convection. At the same time, the results show that the code and the approach give consistent results. Besides, figure 2(a) shows the temporal evolution of mass error
$We_{local} \sim O(1)$. Indeed, in our simulations, the local drop size adjusts correspondingly, so this assumption is fulfilled. The second assumption is that the flow exhibits inertial subrange scaling in the region of wavelengths comparable to the size of the largest drops. The spatial location where this assumption holds in RB convection is in the bulk region of convection (Lohse & Xia Reference Lohse and Xia2010). Therefore, the Kolmogorov–Hinze theory can indeed also be reasonably applied to 2-D RB convection. At the same time, the results show that the code and the approach give consistent results. Besides, figure 2(a) shows the temporal evolution of mass error ![]() $E_{mass}=|M_t-M_0|/M_0$, where
$E_{mass}=|M_t-M_0|/M_0$, where ![]() $M_t$ is the mass of fluid
$M_t$ is the mass of fluid ![]() $H$ at time
$H$ at time ![]() $t$ and
$t$ and ![]() $M_0$ the initial mass. The results indicate good mass conservation.
$M_0$ the initial mass. The results indicate good mass conservation.

Figure 1. Snapshot with the advecting drops in RB convection at density ratio ![]() $\varLambda = 1$ and the system Weber number
$\varLambda = 1$ and the system Weber number ![]() $We=16\,000$. Drops are in grey, and the red and blue lines denote the plates with non-dimensional temperature
$We=16\,000$. Drops are in grey, and the red and blue lines denote the plates with non-dimensional temperature ![]() $\theta =1$ and
$\theta =1$ and ![]() $0$, respectively. The corresponding movie is shown as supplementary material available at https://doi.org/10.1017/jfm.2021.14.
$0$, respectively. The corresponding movie is shown as supplementary material available at https://doi.org/10.1017/jfm.2021.14.

Figure 2. (a) Temporal evolution of mass error ![]() $E_{mass}$ and (b) probability density function (PDF) of the drop size
$E_{mass}$ and (b) probability density function (PDF) of the drop size ![]() $S/D$ at
$S/D$ at ![]() $We=16\,000$, where
$We=16\,000$, where ![]() $D$ is the domain height and
$D$ is the domain height and ![]() $S=2\sqrt {A/{\rm \pi} }$ with
$S=2\sqrt {A/{\rm \pi} }$ with ![]() $A$ being the drop area. (c) Maximal drop size
$A$ being the drop area. (c) Maximal drop size ![]() $S_{max}/D$ as function of
$S_{max}/D$ as function of ![]() $We$, where
$We$, where ![]() $S_{max}$ is measured in the same way as in Hinze (Reference Hinze1955), that is, the diameter of the equivalent drop occupying
$S_{max}$ is measured in the same way as in Hinze (Reference Hinze1955), that is, the diameter of the equivalent drop occupying ![]() $95\,\%$ of the total dispersed area.
$95\,\%$ of the total dispersed area.
4. Interfacial breakup in two-layer turbulent thermal convection
In two-layer RB convection with an initially smooth interface between the two fluids (Xie & Xia Reference Xie and Xia2013), the densities of the fluids depend on both ![]() $\varLambda$ and the local temperature. At small
$\varLambda$ and the local temperature. At small ![]() $\varLambda$, for example, the air–water system with
$\varLambda$, for example, the air–water system with ![]() $\varLambda =0.001$, fluid
$\varLambda =0.001$, fluid ![]() $H$ (water) is always heavier than fluid
$H$ (water) is always heavier than fluid ![]() $L$ (air) even if fluid
$L$ (air) even if fluid ![]() $H$, as the bottom layer, is hotter. In contrast, at large
$H$, as the bottom layer, is hotter. In contrast, at large ![]() $\varLambda$, e.g. an oil–water system with
$\varLambda$, e.g. an oil–water system with ![]() $\varLambda \approx 1$, fluid
$\varLambda \approx 1$, fluid ![]() $H$ (water) is hotter than fluid
$H$ (water) is hotter than fluid ![]() $L$ (oil), so it can be lighter. So, depending on the value of
$L$ (oil), so it can be lighter. So, depending on the value of ![]() $\varLambda$, two distinct types of flow phenomena emerge.
$\varLambda$, two distinct types of flow phenomena emerge.
4.1. First type of interface breakup occurring for small  $\varLambda \ll 1$
$\varLambda \ll 1$
At small ![]() $\varLambda$, fluid
$\varLambda$, fluid ![]() $H$ forms the bottom layer and fluid
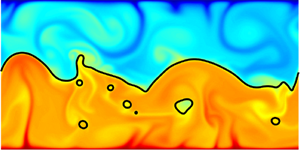
$H$ forms the bottom layer and fluid ![]() $L$ the top one, and large-scale circulations are observed in each layer between the interface and the respective plate, as seen in figure 3(a). With increasing
$L$ the top one, and large-scale circulations are observed in each layer between the interface and the respective plate, as seen in figure 3(a). With increasing ![]() $We$, i.e. decreasing effects of surface tension compared with inertia, the interface becomes more unstable. At low
$We$, i.e. decreasing effects of surface tension compared with inertia, the interface becomes more unstable. At low ![]() $We$ (figure 3a), the interface only slightly deforms because the surface tension is large enough to resist the inertia, such that the convection rolls are well-ordered. The temperature profile is similar to that obtained from two-layer RB convection experiments (Davaille Reference Davaille1999). As
$We$ (figure 3a), the interface only slightly deforms because the surface tension is large enough to resist the inertia, such that the convection rolls are well-ordered. The temperature profile is similar to that obtained from two-layer RB convection experiments (Davaille Reference Davaille1999). As ![]() $We$ increases (figure 3b), the interface undulates due to the plumes. Each crest and trough on the interface is caused by a rising, or, respectively, settling plume in the heavier fluid
$We$ increases (figure 3b), the interface undulates due to the plumes. Each crest and trough on the interface is caused by a rising, or, respectively, settling plume in the heavier fluid ![]() $H$. In this situation, inertia is resisted by gravity together with surface tension. When
$H$. In this situation, inertia is resisted by gravity together with surface tension. When ![]() $We$ keeps increasing (figure 3c), the interface eventually breaks up and drops detach from the interface between two layers.
$We$ keeps increasing (figure 3c), the interface eventually breaks up and drops detach from the interface between two layers.

Figure 3. First type of interface breakup occurring for small ![]() $\varLambda \ll 1$: temperature field and average temperature profile of two-layer RB convection at
$\varLambda \ll 1$: temperature field and average temperature profile of two-layer RB convection at ![]() $\varLambda = 0.3$ for (a)
$\varLambda = 0.3$ for (a) ![]() $We = 5$, (b)
$We = 5$, (b) ![]() $We = 600$ and (c)
$We = 600$ and (c) ![]() $We = 2000$. The corresponding movies are shown as supplementary material.
$We = 2000$. The corresponding movies are shown as supplementary material.
This ‘first type of interface breakup’ (as we call it) occurs at small ![]() $\varLambda$. The process of the breakup begins from a settling plume in fluid
$\varLambda$. The process of the breakup begins from a settling plume in fluid ![]() $H$ thanks to which the interface is pulled downwards, leading to a filament (or trough) on the interface (see figure 4a). If the filament length
$H$ thanks to which the interface is pulled downwards, leading to a filament (or trough) on the interface (see figure 4a). If the filament length ![]() $S_{fila}$ (defined in figure 4a) grows larger than the Hinze length scale
$S_{fila}$ (defined in figure 4a) grows larger than the Hinze length scale ![]() $S_{Hinze}$, the filament will pinch off from the interface. Within the Kolmogrov–Hinze theory (Hinze Reference Hinze1955), the Hinze length scale
$S_{Hinze}$, the filament will pinch off from the interface. Within the Kolmogrov–Hinze theory (Hinze Reference Hinze1955), the Hinze length scale ![]() $S_{Hinze}$ in (3.1) is determined by the energy dissipation rate
$S_{Hinze}$ in (3.1) is determined by the energy dissipation rate ![]() $\epsilon$ of the turbulent flow. As seen from figure 3(c), more drops of fluid
$\epsilon$ of the turbulent flow. As seen from figure 3(c), more drops of fluid ![]() $L$ exist in fluid
$L$ exist in fluid ![]() $H$ than of fluid
$H$ than of fluid ![]() $H$ in fluid
$H$ in fluid ![]() $L$. This finding resembles the breakup of the ocean waves (Deane & Stokes Reference Deane and Stokes2002), leading to more bubbles in water than drops in air. The reason is that
$L$. This finding resembles the breakup of the ocean waves (Deane & Stokes Reference Deane and Stokes2002), leading to more bubbles in water than drops in air. The reason is that ![]() $S_{Hinze}$ is smaller in fluid
$S_{Hinze}$ is smaller in fluid ![]() $H$ than in fluid
$H$ than in fluid ![]() $L$ as
$L$ as ![]() $\rho _H>\rho _L$.
$\rho _H>\rho _L$.

Figure 4. (a) Detachment process of a drop at ![]() $We=2000$. (b) Time-averaged number of the drops of fluid
$We=2000$. (b) Time-averaged number of the drops of fluid ![]() $L$ emerged in fluid
$L$ emerged in fluid ![]() $H$ for various
$H$ for various ![]() $We$, where the empty circles denote the non-breakup regime and stars the breakup regime.
$We$, where the empty circles denote the non-breakup regime and stars the breakup regime.
4.2. Second type of interface breakup occurring for large  $0.5<\varLambda \leqslant 1$
$0.5<\varLambda \leqslant 1$
We now come to the large ![]() $\varLambda \approx 1$ case. Since fluid
$\varLambda \approx 1$ case. Since fluid ![]() $H$ carries hotter fluid than fluid
$H$ carries hotter fluid than fluid ![]() $L$, due to thermal expansion it can become lighter than fluid
$L$, due to thermal expansion it can become lighter than fluid ![]() $L$, inverting the original density contrast at equal temperature. In this situation, buoyancy drives fluid
$L$, inverting the original density contrast at equal temperature. In this situation, buoyancy drives fluid ![]() $H$ upwards and fluid
$H$ upwards and fluid ![]() $L$ downwards. This leads to wave crests and troughs, as shown in figure 5. If
$L$ downwards. This leads to wave crests and troughs, as shown in figure 5. If ![]() $We$ is low (figure 5a), the surface tension can maintain a stable interface, though it is wobbling. However, if
$We$ is low (figure 5a), the surface tension can maintain a stable interface, though it is wobbling. However, if ![]() $We$ increases (figure 5b), the wobbling wave on the interface can amplify more and more until it finally touches the upper and/or lower plate and breaks up. We call this type of interface breakup the ‘second type of breakup’.
$We$ increases (figure 5b), the wobbling wave on the interface can amplify more and more until it finally touches the upper and/or lower plate and breaks up. We call this type of interface breakup the ‘second type of breakup’.

Figure 5. Second type of interface breakup occurring for large ![]() $0.5<\varLambda \leqslant 1$: snapshots at
$0.5<\varLambda \leqslant 1$: snapshots at ![]() $\varLambda = 0.8$ for two different
$\varLambda = 0.8$ for two different ![]() $We$. (a) Wavy interface for
$We$. (a) Wavy interface for ![]() $We = 20$. (b) Breakup and (c) overturning of interface for
$We = 20$. (b) Breakup and (c) overturning of interface for ![]() $We = 30$ at different times
$We = 30$ at different times ![]() $t_1=617$,
$t_1=617$, ![]() $t_2=640$,
$t_2=640$, ![]() $t_3=661$,
$t_3=661$, ![]() $t_4=730$ and
$t_4=730$ and ![]() $t_5=803$. The
$t_5=803$. The ![]() $t_i$ are also marked in figure 6. The colour map is the same as in figure 3. The corresponding movies are shown as supplementary material.
$t_i$ are also marked in figure 6. The colour map is the same as in figure 3. The corresponding movies are shown as supplementary material.
For this second type of interface breakup, the breakup process is strikingly different from the first type. A periodic overturning is observed both in the fluid dynamics and in the heat transfer (see figures 5c and 6): after interface breakup at ![]() $t_1$, fluid
$t_1$, fluid ![]() $H$ initially at the bottom gradually rises above fluid
$H$ initially at the bottom gradually rises above fluid ![]() $L$ and finally contacts the upper cold plate. The increased wetted area of the hotter fluid on the upper cold plate causes a strong enhancement of the Nusselt number
$L$ and finally contacts the upper cold plate. The increased wetted area of the hotter fluid on the upper cold plate causes a strong enhancement of the Nusselt number ![]() $Nu$, in the shown case five times of
$Nu$, in the shown case five times of ![]() $Nu$ without breakup, as shown in figure 6. Then, fluid
$Nu$ without breakup, as shown in figure 6. Then, fluid ![]() $H$ on the top gets cooler and thus heavier, while fluid
$H$ on the top gets cooler and thus heavier, while fluid ![]() $L$ at the bottom gets warmer and thus lighter. Once again, the breakup occurs after
$L$ at the bottom gets warmer and thus lighter. Once again, the breakup occurs after ![]() $t_3$ and the fluids swap their positions (see figure 5c). Since fluid
$t_3$ and the fluids swap their positions (see figure 5c). Since fluid ![]() $L$ is lighter than fluid
$L$ is lighter than fluid ![]() $H$ at the same temperature, it is easier to rise and touch the cold plate. Thus, with fluid
$H$ at the same temperature, it is easier to rise and touch the cold plate. Thus, with fluid ![]() $L$ as the bottom layer, the temperature of the bottom layer during the breakup is lower than that when fluid
$L$ as the bottom layer, the temperature of the bottom layer during the breakup is lower than that when fluid ![]() $H$ is the bottom layer. This is also reflected in the heat transfer. The peak of
$H$ is the bottom layer. This is also reflected in the heat transfer. The peak of ![]() $Nu$ after
$Nu$ after ![]() $t_3$ is smaller, only three times of
$t_3$ is smaller, only three times of ![]() $Nu$ without breakup, and the preparation time for breakup from
$Nu$ without breakup, and the preparation time for breakup from ![]() $t_2$ to
$t_2$ to ![]() $t_3$ is shorter than that from
$t_3$ is shorter than that from ![]() $t_4$ to
$t_4$ to ![]() $t_5$.
$t_5$.

Figure 6. Temporal evolution of the Nusselt number ![]() $Nu$ at the bottom plate for
$Nu$ at the bottom plate for ![]() $We=20$ (black) and
$We=20$ (black) and ![]() $We=30$ (blue). The inset shows a zoom of the temporal evolution of
$We=30$ (blue). The inset shows a zoom of the temporal evolution of ![]() $Nu$ for
$Nu$ for ![]() $We=30$ and the corresponding wetted length
$We=30$ and the corresponding wetted length ![]() $W$ normalized by
$W$ normalized by ![]() $D$ of fluid
$D$ of fluid ![]() $H$ at the top plate.
$H$ at the top plate.
4.3. Critical Weber number for interface breakup
The full phase diagram in the parameter space (![]() $We, \varLambda$) – revealing when and what regime occurs – is plotted in figure 7. When
$We, \varLambda$) – revealing when and what regime occurs – is plotted in figure 7. When ![]() $We$ is larger than a certain critical value
$We$ is larger than a certain critical value ![]() $We_c$, which depends on
$We_c$, which depends on ![]() $\varLambda$, the interface breaks up. It is noteworthy that the transition between the non-breakup and breakup regimes shows two distinct trends, which correspond to the two above identified types of interface breakup, respectively. The natural question that arises here is then: What sets the critical value
$\varLambda$, the interface breaks up. It is noteworthy that the transition between the non-breakup and breakup regimes shows two distinct trends, which correspond to the two above identified types of interface breakup, respectively. The natural question that arises here is then: What sets the critical value ![]() $We_c$ at given
$We_c$ at given ![]() $\varLambda$?
$\varLambda$?

Figure 7. Phase diagram in the ![]() $We\text{--}\varLambda$ parameter space. Empty circles denote the non-breakup regime and stars the interface breakup regime. Symbols with boldface are the cases shown in figures 3 and 5. The grey shadow is a guide to the eye. The red and green lines denote the criteria, (4.3) with prefactor
$We\text{--}\varLambda$ parameter space. Empty circles denote the non-breakup regime and stars the interface breakup regime. Symbols with boldface are the cases shown in figures 3 and 5. The grey shadow is a guide to the eye. The red and green lines denote the criteria, (4.3) with prefactor ![]() $1590$ and (4.6) with prefactor
$1590$ and (4.6) with prefactor ![]() $13.3$, for the first and second type of interface breakup, respectively. The solid parts of the lines, where the theory is supposed to hold, indeed nicely agree with the numerical results.
$13.3$, for the first and second type of interface breakup, respectively. The solid parts of the lines, where the theory is supposed to hold, indeed nicely agree with the numerical results.
In the first type of interface breakup (small ![]() $\varLambda \ll 1$), detaching drops are generated from the initial interface when the filament length
$\varLambda \ll 1$), detaching drops are generated from the initial interface when the filament length ![]() $S_{fila}$ is of the order of the Hinze length scale
$S_{fila}$ is of the order of the Hinze length scale ![]() $S_{Hinze}$. We estimate
$S_{Hinze}$. We estimate ![]() $S_{fila}$ by analysing the force balance: the sum of gravity and surface tension force counteracts the inertial force,
$S_{fila}$ by analysing the force balance: the sum of gravity and surface tension force counteracts the inertial force,
where ![]() $U_H=\sqrt {\alpha g (D/2) (\varDelta /2)}$ and
$U_H=\sqrt {\alpha g (D/2) (\varDelta /2)}$ and ![]() $\delta \rho$ is the density difference from the bottom (fluid
$\delta \rho$ is the density difference from the bottom (fluid ![]() $H$) to the top (fluid
$H$) to the top (fluid ![]() $L$) of the filament. We define
$L$) of the filament. We define ![]() $\delta \rho =\rho _H({T_H}) - \rho _L({T_L})$, where
$\delta \rho =\rho _H({T_H}) - \rho _L({T_L})$, where ![]() $T_i$ is the temperature of fluid
$T_i$ is the temperature of fluid ![]() $i$. We further found that the value of gravity is one order of magnitude greater than surface tension based on the data of cases near the transition region in the first type. This indicates that the generation of the filament is dominated by gravity and inertia. Therefore, we neglect the term
$i$. We further found that the value of gravity is one order of magnitude greater than surface tension based on the data of cases near the transition region in the first type. This indicates that the generation of the filament is dominated by gravity and inertia. Therefore, we neglect the term ![]() $\sigma /S_{fila}$ in (4.1). Note, however, that the surface tension force still plays an important role to determine
$\sigma /S_{fila}$ in (4.1). Note, however, that the surface tension force still plays an important role to determine ![]() $S_{Hinze}$ in (3.1). Combining (4.1), (3.1) and the exact relation
$S_{Hinze}$ in (3.1). Combining (4.1), (3.1) and the exact relation ![]() $\epsilon =(\nu^3 / D^4) (Nu-1) Ra Pr^{-2}$ (Shraiman & Siggia Reference Shraiman and Siggia1990; Ahlers et al. Reference Ahlers, Grossmann and Lohse2009), the dimensionless form of
$\epsilon =(\nu^3 / D^4) (Nu-1) Ra Pr^{-2}$ (Shraiman & Siggia Reference Shraiman and Siggia1990; Ahlers et al. Reference Ahlers, Grossmann and Lohse2009), the dimensionless form of ![]() $S_{fila} \sim S_{Hinze}$ yields
$S_{fila} \sim S_{Hinze}$ yields
 \begin{equation} \left[\left(\frac{1}{Fr}-\theta_H\right)-\varLambda\left(\frac{1}{Fr}-\theta_L \right)\right]^{{-}1} \sim We_c^{-{3/5}}\left(\frac{Nu-1}{\sqrt{RaPr}}\right)^{-{2/5}}, \end{equation}
\begin{equation} \left[\left(\frac{1}{Fr}-\theta_H\right)-\varLambda\left(\frac{1}{Fr}-\theta_L \right)\right]^{{-}1} \sim We_c^{-{3/5}}\left(\frac{Nu-1}{\sqrt{RaPr}}\right)^{-{2/5}}, \end{equation}
with the non-dimensional temperatures ![]() $\theta _i=(T_i-T_c)/\varDelta$ with
$\theta _i=(T_i-T_c)/\varDelta$ with ![]() $i$ being
$i$ being ![]() $H$ and
$H$ and ![]() $L$. Note that
$L$. Note that ![]() $\theta _H$ and
$\theta _H$ and ![]() $\theta _L$ are both taken as
$\theta _L$ are both taken as ![]() $0.5$ given that the filament is generated near the interface, where the temperature is
$0.5$ given that the filament is generated near the interface, where the temperature is ![]() $0.5$. To further simplify (4.2),
$0.5$. To further simplify (4.2), ![]() $Nu$ is regarded as constant because the simulation data show that
$Nu$ is regarded as constant because the simulation data show that ![]() $Nu$ varies only within
$Nu$ varies only within ![]() $15\,\%$ in the non-breakup regime. Given that
$15\,\%$ in the non-breakup regime. Given that ![]() $Nu$,
$Nu$, ![]() $Ra$,
$Ra$, ![]() $Pr$ and
$Pr$ and ![]() $Fr$ are all constant, the criteria for the first type of interface breakup simplifies to
$Fr$ are all constant, the criteria for the first type of interface breakup simplifies to
In the second type of interface breakup (large ![]() $\varLambda \approx 1$), the hot fluid
$\varLambda \approx 1$), the hot fluid ![]() $H$ is lighter than the cold fluid
$H$ is lighter than the cold fluid ![]() $L$, so the buoyancy caused by the unstable temperature stratification can overcome the surface tension, leading to waves on the interface. The buoyancy acting on the wave originates from the density difference between the fluid above and below the wobbling interface (see figure 5). The balance is described by
$L$, so the buoyancy caused by the unstable temperature stratification can overcome the surface tension, leading to waves on the interface. The buoyancy acting on the wave originates from the density difference between the fluid above and below the wobbling interface (see figure 5). The balance is described by
where ![]() $T_i$ is the average temperature in the bulk of fluid
$T_i$ is the average temperature in the bulk of fluid ![]() $i$, and the interface deformation is of the order of
$i$, and the interface deformation is of the order of ![]() $D$ because the breakup occurs when the wave amplitude is larger than half of the plate distance
$D$ because the breakup occurs when the wave amplitude is larger than half of the plate distance ![]() $D$, thus that the interface touches the plates (see figure 5b). The dimensionless form of (4.4) reads
$D$, thus that the interface touches the plates (see figure 5b). The dimensionless form of (4.4) reads
From the temperature profile in figure 3, we estimate ![]() $\theta _H=0.75$ and
$\theta _H=0.75$ and ![]() $\theta _L=0.25$. Then (4.5) simplifies to
$\theta _L=0.25$. Then (4.5) simplifies to
Figure 7 shows that (4.3) and (4.6) indeed well describe the scaling relations of transitions between the non-breakup and breakup regimes.
In the breakup regimes at large ![]() $\varLambda \sim 1$, as
$\varLambda \sim 1$, as ![]() $We$ increases, the periodic overturning of fluid layers gradually becomes chaotic with more and more drops generated from the breakup of the interface. Eventually, the flow pattern is determined by the advection of the small drops (figure 1). There is no clear boundary in the parameter space for this transition and it happens over a considerable range in parameter space. Therefore, in this study, we only focus on when and how the breakup occurs.
$We$ increases, the periodic overturning of fluid layers gradually becomes chaotic with more and more drops generated from the breakup of the interface. Eventually, the flow pattern is determined by the advection of the small drops (figure 1). There is no clear boundary in the parameter space for this transition and it happens over a considerable range in parameter space. Therefore, in this study, we only focus on when and how the breakup occurs.
5. Conclusions
In summary, we have numerically shown two distinct types of interface breakup in two-layer RB convection, which result from different dominant forces. At small ![]() $\varLambda \ll 1$, a filament is generated on the interface due to the competition of inertial force and buoyancy. The interface breaks up in the form of filament detachment when the local filament thicknesses exceed the Hinze length scale. At large
$\varLambda \ll 1$, a filament is generated on the interface due to the competition of inertial force and buoyancy. The interface breaks up in the form of filament detachment when the local filament thicknesses exceed the Hinze length scale. At large ![]() $\varLambda$ with roughly
$\varLambda$ with roughly ![]() $0.5 < \varLambda \leqslant 1$, the periodic overturning-type breakup is caused by buoyancy overwhelming surface tension. From the force balance arguments above, we derive the breakup criteria for the first and second types, respectively. Our approaches show good agreement with the numerical results.
$0.5 < \varLambda \leqslant 1$, the periodic overturning-type breakup is caused by buoyancy overwhelming surface tension. From the force balance arguments above, we derive the breakup criteria for the first and second types, respectively. Our approaches show good agreement with the numerical results.
The threshold of regimes in this work is derived from a force balance argument, which is not limited to 2-D. For 3-D, of course, some expressions need to be modified, for example, surface tension force from ![]() $F_{st}=\sigma /R$ in 2-D to
$F_{st}=\sigma /R$ in 2-D to ![]() $F_{st}=\sigma (1/R_1+1/R_2)$ in 3-D with
$F_{st}=\sigma (1/R_1+1/R_2)$ in 3-D with ![]() $R$,
$R$, ![]() $R_1$ and
$R_1$ and ![]() $R_2$ being the curvature radii. Besides, we also note that previous studies also showed that 2-D and 3-D RB convection have similar features for
$R_2$ being the curvature radii. Besides, we also note that previous studies also showed that 2-D and 3-D RB convection have similar features for ![]() $Pr\geqslant 1$, see van der Poel et al. (Reference van der Poel, Stevens and Lohse2013). Therefore, we expect our results from 2-D flow could be directly extended to 3-D flow.
$Pr\geqslant 1$, see van der Poel et al. (Reference van der Poel, Stevens and Lohse2013). Therefore, we expect our results from 2-D flow could be directly extended to 3-D flow.
Our findings clearly demonstrate that interface breakup in multilayer thermally driven turbulence cannot be solely described by the Kolmogorov–Hinze theory, which is only applicable when the lower layer is much denser than the upper layer or when thermal expansion effects do not play a role. Interestingly, when the lower layer is less dense than the upper layer, the system is unstably stratified, leading to the new breakup type described in this paper where buoyancy and surface tension are the dominant forces. It would be interesting to test our predictions of (4.2) and (4.5) for the transitions between the different regimes in a larger range of the control parameters ![]() $Ra$,
$Ra$, ![]() $Pr$ and
$Pr$ and ![]() $Fr$, which were kept fixed here. More generally, our findings emphasize the role of buoyancy in interfacial breakup. Clearly, buoyancy will also play a prominent role in the interfacial breakup in other turbulent flows, such as Bénard–Marangoni convection, and horizontal and vertical convection. All these phenomena add to the richness of physico-chemical hydrodynamics of droplets far from equilibrium (Lohse & Zhang Reference Lohse and Zhang2020).
$Fr$, which were kept fixed here. More generally, our findings emphasize the role of buoyancy in interfacial breakup. Clearly, buoyancy will also play a prominent role in the interfacial breakup in other turbulent flows, such as Bénard–Marangoni convection, and horizontal and vertical convection. All these phenomena add to the richness of physico-chemical hydrodynamics of droplets far from equilibrium (Lohse & Zhang Reference Lohse and Zhang2020).
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2021.14.
Acknowledgements
We acknowledge PRACE for awarding us access to MareNostrum in Spain at the Barcelona Computing Center (BSC) under the project ![]() $2018194742$. This work was also carried out on the national e-infrastructure of SURFsara, a subsidiary of SURF cooperation, the collaborative ICT organization for Dutch education and research.
$2018194742$. This work was also carried out on the national e-infrastructure of SURFsara, a subsidiary of SURF cooperation, the collaborative ICT organization for Dutch education and research.
Funding
The work was financially supported by ERC-Advanced Grant under the project no. ![]() $740479$.
$740479$.
Declaration of interests
The authors report no conflict of interest.