Article contents
The unifying theory of scaling in thermal convection: the updated prefactors
Published online by Cambridge University Press: 30 July 2013
Abstract
The unifying theory of scaling in thermal convection (Grossmann & Lohse, J. Fluid. Mech., vol. 407, 2000, pp. 27–56; henceforth the GL theory) suggests that there are no pure power laws for the Nusselt and Reynolds numbers as function of the Rayleigh and Prandtl numbers in the experimentally accessible parameter regime. In Grossmann & Lohse (Phys. Rev. Lett., vol. 86, 2001, pp. 3316–3319) the dimensionless parameters of the theory were fitted to 155 experimental data points by Ahlers & Xu (Phys. Rev. Lett., vol. 86, 2001, pp. 3320–3323) in the regime 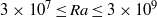 $3\times 1{0}^{7} \leq \mathit{Ra}\leq 3\times 1{0}^{9} $ and
$3\times 1{0}^{7} \leq \mathit{Ra}\leq 3\times 1{0}^{9} $ and 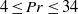 $4\leq \mathit{Pr}\leq 34$ and Grossmann & Lohse (Phys. Rev. E, vol. 66, 2002, p. 016305) used the experimental data point from Qiu & Tong (Phys. Rev. E, vol. 64, 2001, p. 036304) and the fact that
$4\leq \mathit{Pr}\leq 34$ and Grossmann & Lohse (Phys. Rev. E, vol. 66, 2002, p. 016305) used the experimental data point from Qiu & Tong (Phys. Rev. E, vol. 64, 2001, p. 036304) and the fact that 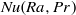 $\mathit{Nu}(\mathit{Ra}, \mathit{Pr})$ is independent of the parameter
$\mathit{Nu}(\mathit{Ra}, \mathit{Pr})$ is independent of the parameter  $a$ , which relates the dimensionless kinetic boundary thickness with the square root of the wind Reynolds number, to fix the Reynolds number dependence. Meanwhile the theory is, on the one hand, well-confirmed through various new experiments and numerical simulations; on the other hand, these new data points provide the basis for an updated fit in a much larger parameter space. Here we pick four well-established (and sufficiently distant)
$a$ , which relates the dimensionless kinetic boundary thickness with the square root of the wind Reynolds number, to fix the Reynolds number dependence. Meanwhile the theory is, on the one hand, well-confirmed through various new experiments and numerical simulations; on the other hand, these new data points provide the basis for an updated fit in a much larger parameter space. Here we pick four well-established (and sufficiently distant) 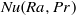 $\mathit{Nu}(\mathit{Ra}, \mathit{Pr})$ data points and show that the resulting
$\mathit{Nu}(\mathit{Ra}, \mathit{Pr})$ data points and show that the resulting 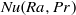 $\mathit{Nu}(\mathit{Ra}, \mathit{Pr})$ function is in agreement with almost all established experimental and numerical data up to the ultimate regime of thermal convection, whose onset also follows from the theory. One extra
$\mathit{Nu}(\mathit{Ra}, \mathit{Pr})$ function is in agreement with almost all established experimental and numerical data up to the ultimate regime of thermal convection, whose onset also follows from the theory. One extra  $\mathit{Re}(\mathit{Ra}, \mathit{Pr})$ data point is used to fix
$\mathit{Re}(\mathit{Ra}, \mathit{Pr})$ data point is used to fix 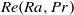 $\mathit{Re}(\mathit{Ra}, \mathit{Pr})$ . As
$\mathit{Re}(\mathit{Ra}, \mathit{Pr})$ . As 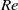 $\mathit{Re}$ can depend on the definition and the aspect ratio, the transformation properties of the GL equations are discussed in order to show how the GL coefficients can easily be adapted to new Reynolds number data while keeping
$\mathit{Re}$ can depend on the definition and the aspect ratio, the transformation properties of the GL equations are discussed in order to show how the GL coefficients can easily be adapted to new Reynolds number data while keeping 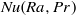 $\mathit{Nu}(\mathit{Ra}, \mathit{Pr})$ unchanged.
$\mathit{Nu}(\mathit{Ra}, \mathit{Pr})$ unchanged.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 222
- Cited by

