Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-18T04:04:52.279Z Has data issue: false hasContentIssue false
  • English
  • Français

Universality of the energy-containing structures in wall-bounded turbulence

Published online by Cambridge University Press:  21 June 2017

Charitha M. de Silva Open the ORCID record for Charitha M. de Silva [Opens in a new window] ,
Dominik Krug Open the ORCID record for Dominik Krug [Opens in a new window] ,
Detlef Lohse Open the ORCID record for Detlef Lohse [Opens in a new window]  and
Ivan Marusic
Charitha M. de Silva*
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
Dominik Krug
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
Detlef Lohse
Affiliation:
Physics of Fluids Group and Twente Max Planck Center, Department of Science and Technology, Mesa+ Institute, and J.M. Burgers Center for Fluid Dynamics, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands Max Planck Institute for Dynamics and Self-Organization, 37077 Göttingen, Germany
Ivan Marusic
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
*
†Email address for correspondence: desilvac@unimelb.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

The scaling behaviour of the longitudinal velocity structure functions 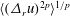$\langle (\unicode[STIX]{x1D6E5}_{r}u)^{2p}\rangle ^{1/p}$ (where 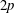$2p$ represents the order) is studied for various wall-bounded turbulent flows. It has been known that for very large Reynolds numbers within the logarithmic region, the structure functions can be described by 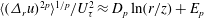$\langle (\unicode[STIX]{x1D6E5}_{r}u)^{2p}\rangle ^{1/p}/U_{\unicode[STIX]{x1D70F}}^{2}\approx D_{p}\ln (r/z)+E_{p}$ (where $r$ is the longitudinal distance, $z$ the distance from the wall, 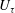$U_{\unicode[STIX]{x1D70F}}$ the friction velocity and 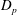$D_{p}$, 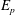$E_{p}$ are constants) in accordance with Townsend’s attached eddy hypothesis. Here we show that the ratios 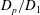$D_{p}/D_{1}$ extracted from plots between structure functions – in the spirit of the extended self-similarity hypothesis – have further reaching universality for the energy containing range of scales. Specifically, we confirm that this description is universal across wall-bounded flows with different flow geometries, and also for both the longitudinal and transversal structure functions, where previously the scaling has been either difficult to discern or differences have been reported when examining the direct representation of 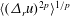$\langle (\unicode[STIX]{x1D6E5}_{r}u)^{2p}\rangle ^{1/p}$. In addition, we present evidence of this universality at much lower Reynolds numbers, which opens up avenues to examine structure functions that are not readily available from high Reynolds number databases.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 823 , 25 July 2017 , pp. 498 - 510
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

del Alamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.Google Scholar
Arneodo, A., Baudet, C., Belin, F., Benzi, R., Castaing, B., Chabaud, B., Chavarria, R., Ciliberto, S., Camussi, R., Chilla, F. et al. 1996 Structure functions in turbulence, in various flow configurations, at Reynolds number between 30 and 5000, using extended self-similarity. Europhys. Lett. 34, 411.Google Scholar
Atkinson, C., Buchmann, N. A. & Soria, J. 2014 An experimental investigation of turbulent convection velocities in a turbulent boundary layer. Flow Turbul. Combust. 94, 1–17.Google Scholar
Belin, F., Tabeling, P. & Willaime, H. 1996 Exponents of the structure function in a low temperature helium experiment. Physica D 93, 52.Google Scholar
Benzi, R., Ciliberto, S., Baudet, C. & Ruiz-Chavarria, G. 1995 On the scaling of three-dimensional homogeneous and isotropic turbulence. Physica D 80, 385–398.Google Scholar
Benzi, R., Ciliberto, S., Tripiccione, R., Baudet, C., Massaioli, F. & Succi, S. 1993 Extended self-similarity in turbulent flows. Phys. Rev. E 48, R29–R32.Google Scholar
Chandran, D., Baidya, R., Monty, J. & Marusic, I. 2017 Two-dimensional energy spectra in high Reynolds number turbulent boundary layers. J. Fluid Mech. (to appear).Google Scholar
Chung, D., Marusic, I., Monty, J. P., Vallikivi, M. & Smits, A. J. 2015 On the universality of inertial energy in the log layer of turbulent boundary layer and pipe flows. Exp. Fluids 56 (7), 1–10.Google Scholar
Chung, D. & McKeon, B. J. 2010 Large-eddy simulation of large-scale structures in long channel flow. J. Fluid Mech. 661, 341–364.Google Scholar
Davidson, P. A., Nickels, T. B. & Krogstad, P.-Å. 2006 The logarithmic structure function law in wall-layer turbulence. J. Fluid Mech. 550, 51–60.Google Scholar
Del Alamo, J. C. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.CrossRefGoogle Scholar
Dennis, D. J. C. & Nickels, T. B. 2008 On the limitations of Taylor’s hypothesis in constructing long structures in a turbulent boundary layer. J. Fluid Mech. 614, 197–206.Google Scholar
Frisch, U. 1995 Turbulence: The Legacy of AN Kolmogorov. Cambridge University Press.Google Scholar
Grossmann, S., Lohse, D. & Reeh, A. 1997a Application of extended self similarity in turbulence. Phys. Rev. E 56, 5473.Google Scholar
Grossmann, S., Lohse, D. & Reeh, A. 1997b Different intermittency for longitudinal and transversal turbulent fluctuations. Phys. Fluids 9, 3817–3825.Google Scholar
Huisman, S. G., Lohse, D. & Sun, C. 2013 Statistics of turbulent fluctuations in counter-rotating Taylor–Couette flows. Phys. Rev. E 88, 063001.Google Scholar
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.Google Scholar
Jacob, B., Biferale, L., Iuso, G. & Casciola, C. M. 2004 Anisotropic fluctuations in turbulent shear flows. Phys. Fluids 16 (11), 4135–4142.Google Scholar
Jiménez, J. 2012 Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44, 27–45.Google Scholar
Kunkel, G. J. & Marusic, I. 2006 Study of the near-wall-turbulent region of the high-Reynolds number boundary layer using an atmospheric flow. J. Fluid Mech. 548, 375–402.Google Scholar
Kurien, S., Lvov, V. S., Procaccia, I. & Sreenivasan, K. R. 2000 Scaling structure of the velocity statistics in atmospheric boundary layers. Phys. Rev. E 61 (1), 407.Google ScholarPubMed
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to Re 𝜏 = 5200. J. Fluid Mech. 774, 395–415.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Meneveau, C. & Marusic, I. 2013 Generalized logarithmic law for high-order moments in turbulent boundary layers. J. Fluid Mech. 719, R1.CrossRefGoogle Scholar
Meneveau, C. & Sreenivasan, K. R. 1987 Simple multifractal cascade model for fully developed turbulence. Phys. Rev. Lett. 59 (13), 1424.Google Scholar
Monty, J. P., Hutchins, N., Ng, H. C. H., Marusic, I. & Chong, M. S. 2009 A comparison of turbulent pipe, channel and boundary layer flows. J. Fluid Mech. 632, 431–442.CrossRefGoogle Scholar
Ng, H. C. H., Monty, J. P., Hutchins, N., Chong, M. S. & Marusic, I. 2011 Comparison of turbulent channel and pipe flows with varying Reynolds number. Exp. Fluids 51 (5), 1261–1281.Google Scholar
Nickels, T. B., Marusic, I., Hafez, S. & Chong, M. S. 2005 Evidence of the k -1 law in a high-Reynolds-number Turbulent Boundary Layer. Phys. Rev. Lett. 95 (7), 074501.Google Scholar
Perry, A. E., Henbest, S. M. & Chong, M. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
She, Z. S. & Leveque, E. 1994 Universal scaling law in fully developed turbulence. Phys. Rev. Lett. 72, 1424.Google Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to 𝛿+ = 2000. Phys. Fluids 25 (10), 105102.Google Scholar
de Silva, C. M., Marusic, I., Woodcock, J. D. & Meneveau, C. 2015 Scaling of second-and higher-order structure functions in turbulent boundary layers. J. Fluid Mech. 769, 654–686.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
van de Water, W. & Herweijer, J. A. 1999 High-order structure functions of turbulence. J. Fluid Mech. 387, 3–37.Google Scholar
Yang, X. I. A., Marusic, I. & Meneveau, C. 2016a Moment generating functions and scaling laws in the inertial layer of turbulent wall-bounded flows. J. Fluid Mech. 791, R2.Google Scholar
Yang, X. I. A., Meneveau, C., Marusic, I. & Biferale, L. 2016b Extended self-similarity in moment-generating-functions in wall-bounded turbulence at high Reynolds number. Phys. Rev. Fluids 1 (4), 044405.Google Scholar