Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-12T01:30:32.420Z Has data issue: false hasContentIssue false
  • English
  • Français

Unsteady effects of strong shock-wave/boundary-layer interaction at high Reynolds number

Published online by Cambridge University Press:  22 June 2017

Vito Pasquariello Open the ORCID record for Vito Pasquariello [Opens in a new window] ,
Stefan Hickel Open the ORCID record for Stefan Hickel [Opens in a new window]  and
Nikolaus A. Adams
Vito Pasquariello*
Affiliation:
Technical University of Munich, Department of Mechanical Engineering, Chair of Aerodynamics and Fluid Mechanics, Boltzmannstr. 15, D-85748 Garching bei München, Germany
Stefan Hickel
Affiliation:
Technische Universiteit Delft, Faculty of Aerospace Engineering, P.O. Box 5058, 2600 GB Delft, The Netherlands
Nikolaus A. Adams
Affiliation:
Technical University of Munich, Department of Mechanical Engineering, Chair of Aerodynamics and Fluid Mechanics, Boltzmannstr. 15, D-85748 Garching bei München, Germany
*
†Email address for correspondence: vito.pasquariello@tum.de
Get access Rights & Permissions [Opens in a new window]

Abstract

We analyse the low-frequency dynamics of a high Reynolds number impinging shock-wave/turbulent boundary-layer interaction (SWBLI) with strong mean-flow separation. The flow configuration for our grid-converged large-eddy simulations (LES) reproduces recent experiments for the interaction of a Mach 3 turbulent boundary layer with an impinging shock that nominally deflects the incoming flow by 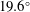$19.6^{\circ }$. The Reynolds number based on the incoming boundary-layer thickness of 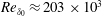$Re_{\unicode[STIX]{x1D6FF}_{0}}\approx 203\times 10^{3}$ is considerably higher than in previous LES studies. The very long integration time of 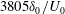$3805\unicode[STIX]{x1D6FF}_{0}/U_{0}$ allows for an accurate analysis of low-frequency unsteady effects. Experimental wall-pressure measurements are in good agreement with the LES data. Both datasets exhibit the distinct plateau within the separated-flow region of a strong SWBLI. The filtered three-dimensional flow field shows clear evidence of counter-rotating streamwise vortices originating in the proximity of the bubble apex. Contrary to previous numerical results on compression ramp configurations, these Görtler-like vortices are not fixed at a specific spanwise position, but rather undergo a slow motion coupled to the separation-bubble dynamics. Consistent with experimental data, power spectral densities (PSD) of wall-pressure probes exhibit a broadband and very energetic low-frequency component associated with the separation-shock unsteadiness. Sparsity-promoting dynamic mode decompositions (SPDMD) for both spanwise-averaged data and wall-plane snapshots yield a classical and well-known low-frequency breathing mode of the separation bubble, as well as a medium-frequency shedding mode responsible for reflected and reattachment shock corrugation. SPDMD of the two-dimensional skin-friction coefficient further identifies streamwise streaks at low frequencies that cause large-scale flapping of the reattachment line. The PSD and SPDMD results of our impinging SWBLI support the theory that an intrinsic mechanism of the interaction zone is responsible for the low-frequency unsteadiness, in which Görtler-like vortices might be seen as a continuous (coherent) forcing for strong SWBLI.

JFM classification

Boundary Layers: Boundary layer separation Turbulent Flows: Compressible turbulence Compressible Flows: Shock waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 823 , 25 July 2017 , pp. 617 - 657
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adams, N. A. 2000 Direct simulation of the turbulent boundary layer along a compression ramp at M = 3 and Re 𝜃 = 1685. J. Fluid Mech. 420, 47–83.CrossRefGoogle Scholar
Agostini, L., Larchevêque, L., Dupont, P., Debiève, J.-F. & Dussauge, J.-P. 2012 Zones of influence and shock motion in a shock/boundary-layer interaction. AIAA J. 50 (6), 1377–1387.CrossRefGoogle Scholar
Andreopoulos, J. & Muck, K. C. 1987 Some new aspects of the shock-wave/boundary-layer interaction in compression-ramp flows. J. Fluid Mech. 180, 405–428.CrossRefGoogle Scholar
Aubard, G., Gloerfelt, X. & Robinet, J.-C. 2013 Large-eddy simulation of broadband unsteadiness in a shock/boundary-layer interaction. AIAA J. 51 (10), 2395–2409.Google Scholar
Beresh, S. J., Clemens, N. T. & Dolling, D. S. 2002 Relationship between upstream turbulent boundary-layer velocity fluctuations and separation shock unsteadiness. AIAA J. 40, 2412–2422.Google Scholar
Bermejo-Moreno, I., Campo, L., Larsson, J., Bodart, J., Helmer, D. & Eaton, J. K. 2014 Confinement effects in shock wave/turbulent boundary layer interactions through wall-modelled large-eddy simulations. J. Fluid Mech. 758, 5–62.Google Scholar
Bookey, P., Wyckham, C., Smits, A. & Martín, M. P. 2005 New experimental data of STBLI at DNS/LES accessible Reynolds numbers. In 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reston, Virigina, pp. 1–18. American Institute of Aeronautics and Astronautics.Google Scholar
Carrière, P., Sirieix, M. & Solignae, J.-L. 1969 Similarity properties of the laminar or turbulent separation phenomena in a non-uniform supersonic flow. In Applied Mechanics – Proceedings of the Twelfth International Congress of Applied Mechanics, pp. 145–157. Springer.Google Scholar
Clemens, N. T. & Narayanaswamy, V. 2009 Shock/turbulent boundary layer interactions: review of recent work on sources of unsteadiness (invited). In 39th AIAA Fluid Dynamics Conference, Reston, Virigina, pp. 1–25. American Institute of Aeronautics and Astronautics.Google Scholar
Clemens, N. T. & Narayanaswamy, V. 2014 Low-frequency unsteadiness of shock wave/turbulent boundary layer interactions. Annu. Rev. Fluid Mech. 46 (1), 469–492.CrossRefGoogle Scholar
Coles, D. E.1962 The turbulent boundary layer in a compressible fluid. Tech. Rep. R-403-PR.Google Scholar
Coles, D. L.1953 Measurements in the boundary layer on a smooth flat plate in supersonic flow. PhD thesis, California Institute of Technology.Google Scholar
Daub, D., Willems, S. & Gülhan, A. 2015 Experimental results on unsteady shock-wave/boundary-layer interaction induced by an impinging shock. CEAS Space J. 8 (1), 3–12.CrossRefGoogle Scholar
Daub, D., Willems, S. & Gülhan, A. 2016 Experiments on the interaction of a fast-moving shock with an elastic panel. AIAA J. 54 (2), 670–678.CrossRefGoogle Scholar
Délery, J. & Dussauge, J.-P. 2009 Some physical aspects of shock wave/boundary layer interactions. Shock Waves 19 (6), 453–468.CrossRefGoogle Scholar
Délery, J. & Marvin, J. G.1986 Shock-wave boundary layer interactions. AGARD-AG Tech. Rep. 280.Google Scholar
Dolling, D. S. 2001 Fifty years of shock-wave/boundary-layer interaction research: what next? AIAA J. 39 (8), 1517–1531.Google Scholar
Dolling, D. S. & Erengil, M. E. 1991 Unsteady wave structure near separation in a Mach 5 compression ramp interaction. AIAA J. 29, 728–735.Google Scholar
Dolling, D. S. & Murphy, M. T. 1983 Unsteadiness of the separation shock wave structure in a supersonic compression ramp flowfield. AIAA J. 21 (12), 1628–1634.CrossRefGoogle Scholar
Dolling, D. S. & Or, C. T. 1985 Unsteadiness of the shock wave structure in attached and separated compression ramp flows. Exp. Fluids 3 (1), 24–32.Google Scholar
van Driest, E. R. 1956 The problem of aerodynamic heating. Aeronaut. Engng Rev. 15, 26–41.Google Scholar
Ducros, F., Ferrand, V., Nicoud, F., Weber, C., Darracq, D., Gacherieu, C. & Poinsot, T. 1999 Large-eddy simulation of the shock/turbulence interaction. J. Comput. Phys. 152 (2), 517–549.Google Scholar
Dupont, P., Haddad, C. & Debiève, J.-F. 2006 Space and time organization in a shock-induced separated boundary layer. J. Fluid Mech. 559, 255–277.CrossRefGoogle Scholar
Dussauge, J.-P., Dupont, P. & Debiève, J.-F. 2006 Unsteadiness in shock wave boundary layer interactions with separation. Aerosp. Sci. Technol. 10 (2), 85–91.Google Scholar
Erdos, J. & Pallone, A. 1963 Shock-boundary layer interaction and flow separations. In Proceedings of the 1962 Heat Transfer and Fluid Mechanics Institute.Google Scholar
Erengil, M. E. & Dolling, D. S.1993 Physical causes of separation shock unsteadiness in shock-wave/turbulent boundary layer interactions. AIAA Paper 93–3134.Google Scholar
Fernholz, H. H. & Finley, P. J.1977 A critical compilation of compressible turbulent boundary layer data. AGARD-AG Tech. Rep. 223.Google Scholar
Floryan, J. M. 1991 On the Görtler instability of boundary layers. Prog. Aerosp. Sci. 28 (3), 235–271.Google Scholar
Ganapathisubramani, B., Clemens, N. T. & Dolling, D. S. 2009 Low-frequency dynamics of shock-induced separation in a compression ramp interaction. J. Fluid Mech. 636, 397–425.Google Scholar
Gatski, T. B. & Bonnet, J.-P. 2009 Compressibility, Turbulence and High Speed Flow. Elsevier.Google Scholar
Ginoux, J. J. 1971 Streamwise vortices in reattaching high-speed flows – A suggested approach. AIAA J. 9 (4), 759–760.Google Scholar
Görtler, H. 1941 Instabilität laminarer Grenzschichten an konkaven Wänden gegenüber gewissen dreidimensionalen Störungen. Z. Angew. Math. Mech. 21 (4), 250–252.Google Scholar
Gottlieb, S. & Shu, C.-W. 1998 Total variation diminishing Runge–Kutta schemes. Math. Comput. Am. Math. Soc. 67 (221), 73–85.CrossRefGoogle Scholar
Grilli, M., Hickel, S. & Adams, N. A. 2013 Large-eddy simulation of a supersonic turbulent boundary layer over a compression expansion ramp. Intl J. Heat Fluid Flow 42, 79–93.CrossRefGoogle Scholar
Grilli, M., Schmid, P. J., Hickel, S. & Adams, N. A. 2012 Analysis of unsteady behaviour in shockwave turbulent boundary layer interaction. J. Fluid Mech. 700, 16–28.CrossRefGoogle Scholar
Guarini, S. E., Moser, R. D., Shariff, K. & Wray, A. 2000 Direct numerical simulation of a supersonic turbulent boundary layer at Mach 2.5. J. Fluid Mech. 414, 1–33.CrossRefGoogle Scholar
Guiho, F., Alizard, F. & Robinet, J.-Ch. 2016 Instabilities in oblique shock wave/laminar boundary-layer interactions. J. Fluid Mech. 789, 1–35.Google Scholar
Hadjadj, A. 2012 Large-eddy simulation of shock/boundary-layer interaction. AIAA J. 50 (12), 2919–2927.CrossRefGoogle Scholar
Hickel, S., Adams, N. A. & Domaradzki, J. A. 2006 An adaptive local deconvolution method for implicit LES. J. Comput. Phys. 213 (1), 413–436.CrossRefGoogle Scholar
Hickel, S., Egerer, C. P. & Larsson, J. 2014 Subgrid-scale modeling for implicit large eddy simulation of compressible flows and shock-turbulence interaction. Phys. Fluids 26 (10), 106101.CrossRefGoogle Scholar
Hopkins, E. J. & Inouye, M. 1971 An evaluation of theories for predicting turbulent skin friction and heat transfer on flat plates at supersonic and hypersonic Mach numbers. AIAA J. 9 (6), 993–1003.CrossRefGoogle Scholar
Hou, Y. X., Clemens, N. T. & Dolling, D.2003 Wide-field study of shock-induced turbulent boundary layer separation. In 41st Aerospace Sciences Meeting and Exhibit, Reno, Nevada. AIAA.Google Scholar
Humble, R. A., Elsinga, G. E., Scarano, F. & van Oudheusden, B. W. 2009 Three-dimensional instantaneous structure of a shock wave/turbulent boundary layer interaction. J. Fluid Mech. 622, 33–62.Google Scholar
Jovanović, M. R., Schmid, P. J. & Nichols, J. W. 2014 Sparsity-promoting dynamic mode decomposition. Phys. Fluids 26 (2), 024103.Google Scholar
Kistler, A. L. 1964 Fluctuating wall pressure under a separated supersonic flow. J. Acoust. Soc. Am. 36 (3), 543–550.CrossRefGoogle Scholar
Klein, M., Sadiki, A. & Janicka, J. 2003 A digital filter based generation of inflow data for spatially developing direct numerical or large Eddy simulations. J. Comput. Phys. 186, 652–665.CrossRefGoogle Scholar
Komminaho, J. & Skote, M. 2002 Reynolds stress budgets in Couette and boundary layer flows. Flow Turbul. Combust. 68 (2), 167–192.CrossRefGoogle Scholar
Kottke, V. 1988 On the instability of laminar boundary layers along concave walls towards Görtler vortices. In Propagation in Systems Far from Equilibrium, Springer Series in Synergetics, Berlin, Heidelberg, vol. 41, pp. 390–398. Springer.Google Scholar
Lesieur, M., Métais, O. & Comte, P. 2005 Large-Eddy Simulations of Turbulence. Cambridge University Press.Google Scholar
Loginov, M. S., Adams, N. A. & Zheltovodov, A. A. 2006 Large-eddy simulation of shock-wave/turbulent-boundary-layer interaction. J. Fluid Mech. 565, 135.Google Scholar
Maeder, T., Adams, N. A. & Kleiser, L. 2001 Direct simulation of turbulent supersonic boundary layers by an extended temporal approach. J. Fluid Mech. 429, 187–216.CrossRefGoogle Scholar
Matheis, J. & Hickel, S. 2015 On the transition between regular and irregular shock patterns of shock-wave/boundary-layer interactions. J. Fluid Mech. 776, 200–234.Google Scholar
Morgan, B., Duraisamy, K., Nguyen, N., Kawai, S. & Lele, S. K. 2013 Flow physics and RANS modelling of oblique shock/turbulent boundary layer interaction. J. Fluid Mech. 729, 231–284.Google Scholar
Naidoo, K. & Skews, B. W. 2011 Dynamic effects on the transition between two-dimensional regular and Mach reflection of shock waves in an ideal, steady supersonic free stream. J. Fluid Mech. 676, 432–460.Google Scholar
Nichols, J. W., Larsson, J., Bernardini, M. & Pirozzoli, S. 2016 Stability and modal analysis of shock/boundary layer interactions. Theor. Comput. Fluid Dyn. 31 (1), 33–50.CrossRefGoogle Scholar
Pasquariello, V., Grilli, M., Hickel, S. & Adams, N. A. 2014 Large-eddy simulation of passive shock-wave/boundary-layer interaction control. Intl J. Heat Fluid Flow 49, 116–127.CrossRefGoogle Scholar
Piponniau, S., Dussauge, J.-P., Debiève, J.-F. & Dupont, P. 2009 A simple model for low-frequency unsteadiness in shock-induced separation. J. Fluid Mech. 629, 87.Google Scholar
Pirozzoli, S. & Bernardini, M. 2011 Turbulence in supersonic boundary layers at moderate Reynolds number. J. Fluid Mech. 688, 120–168.CrossRefGoogle Scholar
Pirozzoli, S. & Grasso, F. 2006 Direct numerical simulation of impinging shock wave/turbulent boundary layer interaction at M = 2. 25. Phys. Fluids 18 (6), 065113.CrossRefGoogle Scholar
Pirozzoli, S., Grasso, F. & Gatski, T. B. 2004 Direct numerical simulation and analysis of a spatially evolving supersonic turbulent boundary layer at M = 2. 25. Phys. Fluids 16 (3), 530–545.CrossRefGoogle Scholar
Pirozzoli, S., Larsson, J., Nichols, J. W., Morgan, B. E. & Lele, S. K. 2010 Analysis of unsteady effects in shock/boundary layer interactions. In Proceedings of the 2010 CTR Summer Program. Center of Turbulence Research.Google Scholar
Plotkin, K. J. 1975 Shock wave oscillation driven by turbulent boundary-layer fluctuations. AIAA J. 13 (8), 1036–1040.Google Scholar
Priebe, S. & Martín, M. P. 2012 Low-frequency unsteadiness in shock wave-turbulent boundary layer interaction. J. Fluid Mech. 699, 1–49.CrossRefGoogle Scholar
Priebe, S., Tu, J. H., Rowley, C. W. & Martín, M. P. 2016 Low-frequency dynamics in a shock-induced separated flow. J. Fluid Mech. 807, 441–477.Google Scholar
Priebe, S., Wu, M. & Martín, M. P. 2009 Direct numerical simulation of a reflected-shock-wave/turbulent-boundary-layer interaction. AIAA J. 47 (5), 1173–1185.Google Scholar
Quaatz, J. F., Giglmaier, M., Hickel, S. & Adams, N. A. 2014 Large-eddy simulation of a pseudo-shock system in a Laval nozzle. Intl J. Heat Fluid Flow 49, 108–115.Google Scholar
Ringuette, M. J., Bookey, P. B., Wyckham, C. & Smits, A. J. 2009 Experimental study of a Mach 3 compression ramp interaction at Re 𝜃 = 2400. AIAA J. 47 (2), 373–385.Google Scholar
Rowley, C. W., Mezić, I., Bagheri, S., Schlatter, P. & Henningson, D. S. 2009 Spectral analysis of nonlinear flows. J. Fluid Mech. 641, 115–127.Google Scholar
Sandham, N. D. 2016 Effects of compressibility and shock-wave interactions on turbulent shear flows. Flow Turbul. Combust. 97 (1), 1–25.Google Scholar
Sansica, A., Sandham, N. D. & Hu, Z. 2014 Forced response of a laminar shock-induced separation bubble. Phys. Fluids 26 (9), 093601.Google Scholar
Schlatter, P. & Örlü, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.CrossRefGoogle Scholar
Schmid, P. J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.Google Scholar
Schülein, E. & Trofimov, V. M. 2011 Steady longitudinal vortices in supersonic turbulent separated flows. J. Fluid Mech. 672, 451–476.Google Scholar
Selig, M. S., Andreopoulos, J., Muck, K. C., Dussauge, J. P. & Smits, A. J. 1989 Turbulence structure in a shock wave/turbulent boundary-layer interaction. AIAA J. 27 (7), 862–869.CrossRefGoogle Scholar
Simens, M. P., Jiménez, J., Hoyas, S. & Mizuno, Y. 2009 A high-resolution code for turbulent boundary layers. J. Comput. Phys. 228 (11), 4218–4231.CrossRefGoogle Scholar
Smits, A. J. & Dussauge, J.-P. 2006 Turbulent Shear Layers in Supersonic Flow. Springer.Google Scholar
Smits, A. J., Matheson, N. & Joubert, P. N. 1983 Low-Reynolds-number turbulent boundary layers in zero and favorable pressure gradients. J. Ship Res. 27, 147–157.CrossRefGoogle Scholar
Souverein, L. J., Dupont, P., Debiève, J.-F., Dussauge, J.-P., van Oudheusden, B. W. & Scarano, F. 2010 Effect of interaction strength on unsteadiness in turbulent shock-wave-induced separations. AIAA J. 48 (7), 1480–1493.Google Scholar
Stolz, S. & Adams, N. A. 2003 Large-eddy simulation of high-Reynolds-number supersonic boundary layers using the approximate deconvolution model and a rescaling and recycling technique. Phys. Fluids 15 (8), 2398.Google Scholar
Thomas, F. O., Putnam, C. M. & Chu, H. C. 1994 On the mechanism of unsteady shock oscillation in shock wave/turbulent boundary layer interactions. Exp. Fluids 18‐18 (1–2), 69–81.CrossRefGoogle Scholar
Touber, E. & Sandham, N. D. 2009 Large-eddy simulation of low-frequency unsteadiness in a turbulent shock-induced separation bubble. Theor. Comput. Fluid Dyn. 23 (2), 79–107.Google Scholar
Touber, E. & Sandham, N. D. 2011 Low-order stochastic modelling of low-frequency motions in reflected shock-wave/boundary-layer interactions. J. Fluid Mech. 671, 417–465.CrossRefGoogle Scholar
Tu, J. H.2013 On dynamic mode decomposition: theory and applications. PhD thesis, Princeton University.Google Scholar
Tu, J. H. & Rowley, C. W. 2012 An improved algorithm for balanced POD through an analytic treatment of impulse response tails. J. Comput. Phys. 231 (16), 5317–5333.CrossRefGoogle Scholar
Ünalmis, O. & Dolling, D.1994 Decay of wall pressure field and structure of a Mach 5 adiabatic turbulent boundary layer. In Fluid Dynamics Conference, Reston, Virigina. AIAA.Google Scholar
Wang, B., Sandham, N. D., Hu, Z. & Liu, W. 2015 Numerical study of oblique shock-wave/boundary-layer interaction considering sidewall effects. J. Fluid Mech. 767, 526–561.Google Scholar
Willems, S.2016 Strömung-Struktur-Wechselwirkung in Überschallströmungen. PhD thesis, German Aerospace Center (DLR).Google Scholar
Wu, M. & Martín, M. P. 2008 Analysis of shock motion in shockwave and turbulent boundary layer interaction using direct numerical simulation data. J. Fluid Mech. 594, 71–83.Google Scholar
Zukoski, E. E. 1967 Turbulent boundary-layer separation in front of a forward-facing step. AIAA J. 5 (10), 1746–1753.Google Scholar

Pasquariello et al. supplementary movie

DMD analysis of spanwise-averaged snapshots. Flow modulation by means of mode Φ1. The animation shows contours of the pressure gradient magnitude in the range │∇p│δ0/p∞ = [0,10] at 8 equally spaced phase angles. The mean shock system together with the instantaneous separation bubble are highlighted by black solid lines.

Download Pasquariello et al. supplementary movie(Video)
Video 1.2 MB

Pasquariello et al. supplementary movie

DMD analysis of spanwise-averaged snapshots. Flow modulation by means of mode Φ2. The animation shows contours of the pressure gradient magnitude in the range │∇p│δ0/p∞ = [0,10] at 8 equally spaced phase angles. The mean shock system together with the instantaneous separation bubble are highlighted by black solid lines.

Download Pasquariello et al. supplementary movie(Video)
Video 1.1 MB

Pasquariello et al. supplementary movie

DMD analysis of spanwise-averaged snapshots. Flow modulation by means of mode Φ3. The animation shows contours of the pressure gradient magnitude in the range │∇p│δ0/p∞ = [0,10] at 8 equally spaced phase angles. The mean shock system together with the instantaneous separation bubble are highlighted by black solid lines.

Download Pasquariello et al. supplementary movie(Video)
Video 864.2 KB

Pasquariello et al. supplementary movie

MDMD analysis of spanwise-averaged snapshots. Flow modulation by means of mode Φ4. The animation shows contours of the pressure gradient magnitude in the range │∇p│δ0/p∞ = [0,10] at 8 equally spaced phase angles. The mean shock system together with the instantaneous separation bubble are highlighted by black solid lines.

Download Pasquariello et al. supplementary movie(Video)
Video 796.4 KB

Pasquariello et al. supplementary movie

DMD analysis of wall-plane snapshots. Flow modulation by means of mode Φ1. The animation shows contours of the two-dimensional skin-friction coefficient at 8 equally spaced phase angles. The instantaneous separation and reattachment locations are highlighted by black solid lines.

Download Pasquariello et al. supplementary movie(Video)
Video 2.5 MB

Pasquariello et al. supplementary movie

DMD analysis of wall-plane snapshots. Flow modulation by means of mode Φ2. The animation shows contours of the two-dimensional skin-friction coefficient at 8 equally spaced phase angles. The instantaneous separation and reattachment locations are highlighted by black solid lines.

Download Pasquariello et al. supplementary movie(Video)
Video 2.3 MB

Pasquariello et al. supplementary movie

DMD analysis of wall-plane snapshots. Flow modulation by means of mode Φ3. The animation shows contours of the two-dimensional skin-friction coefficient at 8 equally spaced phase angles. The instantaneous separation and reattachment locations are highlighted by black solid lines.

Download Pasquariello et al. supplementary movie(Video)
Video 1.6 MB

Pasquariello et al. supplementary movie

DMD analysis of wall-plane snapshots. Flow modulation by means of mode Φ3. The animation shows contours of the two-dimensional skin-friction coefficient at 8 equally spaced phase angles. The instantaneous separation and reattachment locations are highlighted by black solid lines.

Download Pasquariello et al. supplementary movie(Video)
Video 1.6 MB