Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Cho, Seongwook
and
Son, Gihun
2018.
Numerical simulation of acoustic droplet vaporization near a wall.
International Communications in Heat and Mass Transfer,
Vol. 99,
Issue. ,
p.
7.
Li, Tong
Zhang, A-Man
Wang, Shi-Ping
Chen, Guo-Qing
and
Li, Shuai
2019.
Nonlinear interaction and coalescence features of oscillating bubble pairs: Experimental and numerical study.
Physics of Fluids,
Vol. 31,
Issue. 9,
Fuster, D.
2019.
A Review of Models for Bubble Clusters in Cavitating Flows.
Flow, Turbulence and Combustion,
Vol. 102,
Issue. 3,
p.
497.
Ye, Yuemei
Klimchuk, Stanislav
Shang, Mingwei
McDonald, Kenneth
and
Niu, Junjie
2019.
Acoustic Bubble Suppression by Constructing a Hydrophilic Coating on HDPE Surface.
ACS Applied Materials & Interfaces,
Vol. 11,
Issue. 18,
p.
16944.
Reuter, Fabian
and
Kaiser, Sebastian A.
2019.
High-speed film-thickness measurements between a collapsing cavitation bubble and a solid surface with total internal reflection shadowmetry.
Physics of Fluids,
Vol. 31,
Issue. 9,
Zhang, Yu-ning
Li, Xiao-fei
Guo, Zhong-yu
and
Zhang, Yu-ning
2019.
Interior non-uniformity of acoustically excited oscillating gas bubbles.
Journal of Hydrodynamics,
Vol. 31,
Issue. 4,
p.
725.
Li, Tong
Zhang, A-Man
Wang, Shi-Ping
Li, Shuai
and
Liu, Wen-Tao
2019.
Bubble interactions and bursting behaviors near a free surface.
Physics of Fluids,
Vol. 31,
Issue. 4,
Yamashita, Tatsuya
and
Ando, Keita
2019.
Low-intensity ultrasound induced cavitation and streaming in oxygen-supersaturated water: Role of cavitation bubbles as physical cleaning agents.
Ultrasonics Sonochemistry,
Vol. 52,
Issue. ,
p.
268.
Barcikowski, Stephan
Plech, Anton
Suslick, Kenneth S.
and
Vogel, Alfred
2019.
Materials synthesis in a bubble.
MRS Bulletin,
Vol. 44,
Issue. 5,
p.
382.
Li, Xiaofei
Duan, Yaxin
Zhang, Yuning
Tang, Ningning
and
Zhang, Yuning
2019.
Retardant Effects of Collapsing Dynamics of a Laser-Induced Cavitation Bubble Near a Solid Wall.
Symmetry,
Vol. 11,
Issue. 8,
p.
1051.
Kordel, Stephan
and
Hussong, Jeanette
2019.
Utilizing differential interferometry for spatially resolved pressure field measurements of laser-induced cavitation.
Experiments in Fluids,
Vol. 60,
Issue. 1,
Denner, Fabian
Evrard, Fabien
and
van Wachem, Berend
2020.
Modeling Acoustic Cavitation Using a Pressure-Based Algorithm for Polytropic Fluids.
Fluids,
Vol. 5,
Issue. 2,
p.
69.
Sun, Xun
Liu, Jingting
Ji, Li
Wang, Guichao
Zhao, Shan
Yoon, Joon Yong
and
Chen, Songying
2020.
A review on hydrodynamic cavitation disinfection: The current state of knowledge.
Science of The Total Environment,
Vol. 737,
Issue. ,
p.
139606.
Zeng, Qingyun
Gonzalez-Avila, Silvestre Roberto
and
Ohl, Claus-Dieter
2020.
Splitting and jetting of cavitation bubbles in thin gaps.
Journal of Fluid Mechanics,
Vol. 896,
Issue. ,
Wu, Hao
Chisholm, Carly F.
Puryear, Meagen
Movafaghi, Sanli
Smith, Samuel D.
Pokhilchuk, Yekaterina
Lengsfeld, Corinne S.
and
Randolph, Theodore W.
2020.
Container Surfaces Control Initiation of Cavitation and Resulting Particle Formation in Protein Formulations After Application of Mechanical Shock.
Journal of Pharmaceutical Sciences,
Vol. 109,
Issue. 3,
p.
1270.
Vyas, N.
Wang, Q.X.
Manmi, K.A.
Sammons, R.L.
Kuehne, S.A.
and
Walmsley, A.D.
2020.
How does ultrasonic cavitation remove dental bacterial biofilm?.
Ultrasonics Sonochemistry,
Vol. 67,
Issue. ,
p.
105112.
Tyurnina, Anastasia V.
Tzanakis, Iakovos
Morton, Justin
Mi, Jiawei
Porfyrakis, Kyriakos
Maciejewska, Barbara M.
Grobert, Nicole
and
Eskin, Dmitry G.
2020.
Ultrasonic exfoliation of graphene in water: A key parameter study.
Carbon,
Vol. 168,
Issue. ,
p.
737.
Oyarte Gálvez, Loreto
Fraters, Arjan
Offerhaus, Herman L.
Versluis, Michel
Hunter, Ian W.
and
Fernández Rivas, David
2020.
Microfluidics control the ballistic energy of thermocavitation liquid jets for needle-free injections.
Journal of Applied Physics,
Vol. 127,
Issue. 10,
Chu, Chun-Lin
Lu, Te-Yun
and
Fuh, Yiin-Kuen
2020.
The suitability of ultrasonic and megasonic cleaning of nanoscale patterns in ammonia hydroxide solutions for particle removal and feature damage.
Semiconductor Science and Technology,
Vol. 35,
Issue. 4,
p.
045001.
Li, Shuai
Prosperetti, Andrea
and
van der Meer, Devaraj
2020.
Dynamics of a toroidal bubble on a cylinder surface with an application to geophysical exploration.
International Journal of Multiphase Flow,
Vol. 129,
Issue. ,
p.
103335.
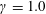 $\unicode[STIX]{x1D6FE}=1.0$ (
$\unicode[STIX]{x1D6FE}=1.0$ ( $\unicode[STIX]{x1D6FE}=h/R_{max}$ , where
$\unicode[STIX]{x1D6FE}=h/R_{max}$ , where 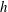 $h$ is the distance of the initial bubble centre to the boundary, and
$h$ is the distance of the initial bubble centre to the boundary, and 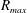 $R_{max}$ is the maximum spherical equivalent radius of the bubble). The calculation of the wall shear stress is found to be reliable once the flow region with constant shear rate in the boundary layer is determined. Very high wall shear stresses of 100 kPa are found during the early spreading of the jet, followed by complex flows composed of annular stagnation rings and secondary vortices. Although the simulated bubble dynamics agrees very well with experiments, we obtain only qualitative agreement with experiments due to inherent experimental challenges.
$R_{max}$ is the maximum spherical equivalent radius of the bubble). The calculation of the wall shear stress is found to be reliable once the flow region with constant shear rate in the boundary layer is determined. Very high wall shear stresses of 100 kPa are found during the early spreading of the jet, followed by complex flows composed of annular stagnation rings and secondary vortices. Although the simulated bubble dynamics agrees very well with experiments, we obtain only qualitative agreement with experiments due to inherent experimental challenges.