Article contents
Scale-dependent pop-ins in nanoindentation and scale-free plastic fluctuations in microcompression
Published online by Cambridge University Press: 10 January 2020
Abstract
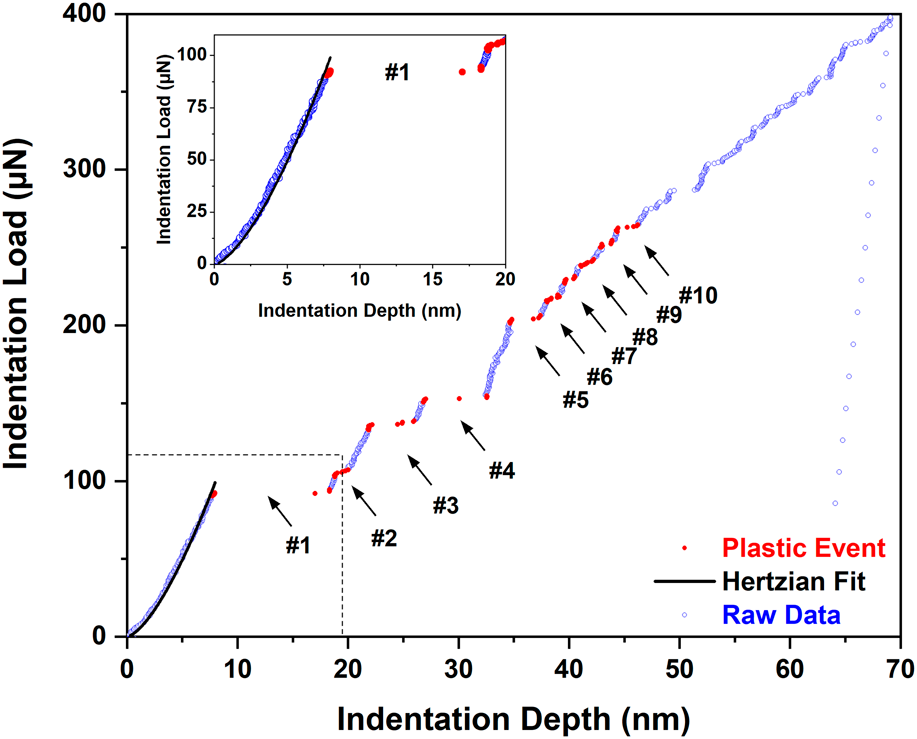
Nanoindentation and microcrystal deformation are two methods that allow probing size effects in crystal plasticity. In many cases of microcrystal deformation, scale-free and potentially universal intermittency of event sizes during plastic flow has been revealed, whereas nanoindentation has been mainly used to assess the stress statistics of the first pop-in. Here, we show that both methods of deformation exhibit fundamentally different event-size statistics obtained from plastic instabilities. Nanoindentation results in scale-dependent intermittent microplasticity best described by Weibull statistics (stress and magnitude of the first pop-in) and lognormal statistics (magnitude of higher-order pop-ins). In contrast, finite-volume microcrystal deformation of the same material exhibits microplastic event-size intermittency of truncated power-law type even when the same plastic volume as in nanoindentation is probed. Furthermore, we successfully test a previously proposed extreme-value statistics model that relates the average first critical stress to the shape and scale parameter of the underlying Weibull distribution.
Keywords
Information
- Type
- Article
- Information
- Copyright
- Copyright © Materials Research Society 2020
References
- 11
- Cited by


