Article contents
Analysis of local grain boundary strengthening utilizing the extrinsic indentation size effect
Published online by Cambridge University Press: 14 May 2019
Abstract
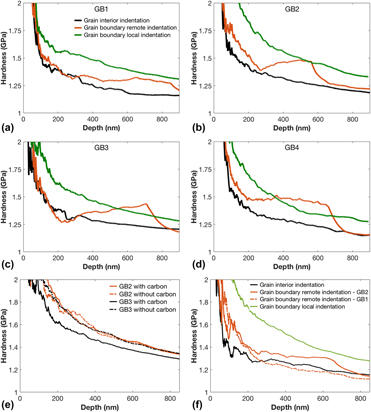
The extrinsic indentation size effect (ISE) is utilized to analyze the depth-dependent hardness for Berkovich indentation of non-uniform dislocation distributions with one and two dimensional deformation gradients and is then extended to indentation results at grain boundaries. The role of the Berkovich pyramid orientation and placement relative to the grain boundary on extrinsic ISE is considered in terms of slip transmission at yield and plastic incompatibility during post-yield deformation. The results are interpreted using a local dislocation hardening mechanism originally proposed by Ashby, combined with the Hall–Petch equation. The Hall–Petch coefficient determined from the extrinsic ISE of the grain boundary is found to be consistent with the published values for pure Fe and mild steel. A simple, linear continuum strain gradient plasticity model is used to further analyze the results to include contributions from a non-uniform distribution in plastic strain and dislocation density.
Information
- Type
- Article
- Information
- Journal of Materials Research , Volume 34 , Issue 13: Focus Issue: Intrinsic and Extrinsic Size Effects in Materials , 15 July 2019 , pp. 2347 - 2369
- Copyright
- Copyright © Materials Research Society 2019
Footnotes
This author was an editor of this journal during the review and decision stage. For the JMR policy on review and publication of manuscripts authored by editors, please refer to http://www.mrs.org/editor-manuscripts/.
References
- 7
- Cited by

