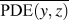I. INTRODUCTION
Fundamentally understanding thermal transport in polymers is essential for tuning thermal conductivity and accelerating their various applications such as thermal management and energy conversion.Reference Aricò, Bruce, Scrosati, Tarascon and van Schalkwijk1–Reference Liao, Liu, Liu, Deng and Yang5 The morphology and topology of polymers were found to be essential to their thermal conductivity.Reference Ma and Tian6 Amorphous bulk polymers typically show a very low thermal conductivity of k ∼ 0.1 W/(mK)Reference Choy7 and have been widely used as thermal insulators. However, aligning polymer chains can significantly reduce phonon scattering and enhance thermal conductivity along their chain direction.Reference Choy, Chen and Luk8–Reference Hansen and Bernier10 Extremely high thermal conductivity of a single polyethylene (PE) chain was predicted using molecular dynamics (MD) simulations.Reference Henry and Chen11 A PE nanofiber of 50–500 nm diameter was reported to have a thermal conductivity as high as 104 W/(mK) using a bimaterial AFM microcantilever technique.Reference Shen, Henry, Tong, Zheng and Chen12 Recently, crystalline PE and liquid crystalline poly(p-phenylene benzobisoxazole) fibers with diameters of 10–30 μm were reported to have a high thermal conductivity of around 20 W/(mK) using the time-domain thermoreflectance technique.Reference Wang, Ho, Segalman and Cahill13
Despite alignment, thermal conductivity among different crystalline or single-chain polymers varies by two orders of magnitude at room temperature. It is desired to identify the key factors that dominate the thermal transport in aligned polymer chains. Polymer nanofibers with rigid backbones, exemplified by π-conjugated polymers, were found to have high thermal conductivity and good thermal stability due to suppressed segmental rotations and large phonon group velocities.Reference Zhang, Wu and Luo14 The length-dependent thermal conductivity of two types of single extended polymer chains was correlated with the orientational parameters P 2b and P 2rot that characterize the backbone alignment and the planar aromatic ring rotation, respectively.Reference Liu and Yang15 Nevertheless, the effects of chain rotation on thermal conductivity of single-chain polymers have not been studied in depth.
Kevlar (polyparaphenylene terephthalamide) is known as a light-weight and strong synthetic fiber with high tensile strength and Young's modulus.Reference Reed and Golda16 Experimentally, Kevlar 49 fibers were measured to have a thermal conductivity of 4.0 W/(mK) at 290 K.Reference Ventura and Martelli17 The thermal conductivity of Kevlar 149 fibers was measured to be 3.2 W/(mK) with tensile modulus of 120 GPa.Reference Wang, Ho, Segalman and Cahill13 Computationally, crystalline Kevlar fibers were calculated to have a thermal conductivity of 8.05 W/mK using MD simulations.Reference Zhang, Wu and Luo14 PBDT [poly(2,2′-disulfonyl-4,4′-benzidine terephthalamide)] is a water-soluble semirigid polyanion.Reference Yu, He, Wang, Madsen and Qiao18 PBDT-derivative polymers are obtained by changing functional groups of PBDT at phenyl rings. Thermal conductivity of single-chain Kevlar and PBDT-derivatives remains unknown.
What is the specific role of chain rotation in thermal conductivity of single-chain polymers? To address this question, we studied chain rotation effects on thermal conductivity of single-chain polymers made of Kevlar and PBDT-derivatives. We carefully chose Kevlar and PBDT-derivatives because they have very similar chemical structures with aromatic rings, where we can pin down the effects of chain rotation. The reason we focus on single-chain polymers is to isolate the chain rotation effects from chain–chain interactions. Using equilibrium molecular dynamics (EMD) method, we studied thermal conductivity along the chain direction, i.e., x direction, k x, of stretched and unstretched single-chain polymers. Note that the intention of this work is not to study the effects of stretching. Stretching is just a way to generate different levels of chain rotation. We found that chain rotation is essential for reducing k x. Large chain rotation leads to small k x. By defining a new chain rotation factor (CRF), we can quantify the rotation level and correlate k x with chain rotation in a simple but reliable way. We further calculated phonon dispersions of all the polymers and attributed the reduced thermal conductivity to decreased phonon group velocities and shortened phonon mean free paths. Moreover, functional groups in PBDT-derivative polymers play a crucial role in chain rotation. By merely changing functional groups, the CRF can change by a factor of 1.4 and correspondingly, thermal conductivity can vary by 3.6 times for unstretched single-chain polymers and 4.9 times for stretched single-chain polymers. Our results offer useful insights into one of the fundamental mechanisms that govern the thermal conductivity of single-chain polymers, allowing us to design polymers with desired thermal transport properties by controlling their chain rotation levels.
II. METHOD
The chemical structures of Kevlar and PBDT-derivatives are shown in Fig. 1. We also included the structure of PBDT as a reference. We did not simulate PBDT because it contains –SO3− and Na+, and polymer consistent force-field (PCFF) potential cannot handle ionic bonds. All the polymers were built in Materials Studio.19 Single chains were placed all along the x direction, and the unit cell length in the x direction for unstretched and stretched structures is summarized in Table I. The stretched single-chain polymers were achieved by artificially enlarging the unit cells of their unstretched counterparts. The unit cell length in y and z directions was set to be 50 Å to prevent interaction between neighboring polymer chains. We optimized unit cell of all the structures using PCFF within Materials Studio. PCFF, a class II potential which includes anharmonic bonding terms,Reference Hill and Sauer20,Reference Chang, Yoshioka, Kanezashi, Tsuru and Tung21 is intended for applications in polymers and organic material.Reference Ma and Tian6,Reference Ma, O’Donnel and Tian22–Reference Ma and Tian24 The size of supercells used to calculate k x in this study also can be found in Table I. We intentionally set the supercells of these single-chain polymers to be large enough to rule out size effects. Periodic boundary conditions were applied in the x, y, and z directions. The stretch ratio was calculated using the length difference between unstretched and stretched polymers divided by the initial length of the unstretched polymers. We kept the stretch ratio around 10% to make sure that none of the bonds were broken. EMD simulationsReference Ma and Tian24 were performed on each structure with PCFF potential using LAMMPS.Reference Plimpton25 EMD simulations keep a uniform temperature throughout the system, and k x along the polymer chain direction is calculated by the autocorrelation of instantaneous heat flux through the Green–Kubo formula based on linear response theory, as shown in the following equationReference Green26,Reference Green27 :
where k x is the thermal conductivity along the x direction, i.e., along the polymer chain direction, V is the volume of the simulated system, k B is the Boltzmann constant, T is the absolute temperature (300 K in this study), J x is the heat flux along the x direction, and τ is the delay time. Because we set the y and z directions to be arterially large, we could not directly use the volume of the simulation box as V. Instead, we needed to calculate the effective volume of the polymer chains using the densities of their bulk amorphous structures,Reference Liu and Yang15 which is a typical practice to deal with single-chain systems. The densities of amorphous Kevlar and PBDT are 1.44 g/cm3 and 1.50 g/cm3, respectively.Reference Nilakantan, Obaid, Keefe and Gillespie28,Reference Wang, Gao, Dingemans and Madsen29 We approximated the densities of amorphous PBDT-H, PBDT-COOH, and PBDT-OCOOH to that of PBDT because the only differences are the functional groups. We extracted k x by averaging over ten identical simulations with different random initial velocities for each polymer. Timestep was set to be 0.5 fs and the cutoff distance of the Lennard–Jones interaction was 10 Å. Each system was relaxed a canonical ensemble (NVT) followed by a microcanonical ensemble (NVE), each for 500 ps. Heat flux data were then collected in an NVE ensemble for another 2 ns.
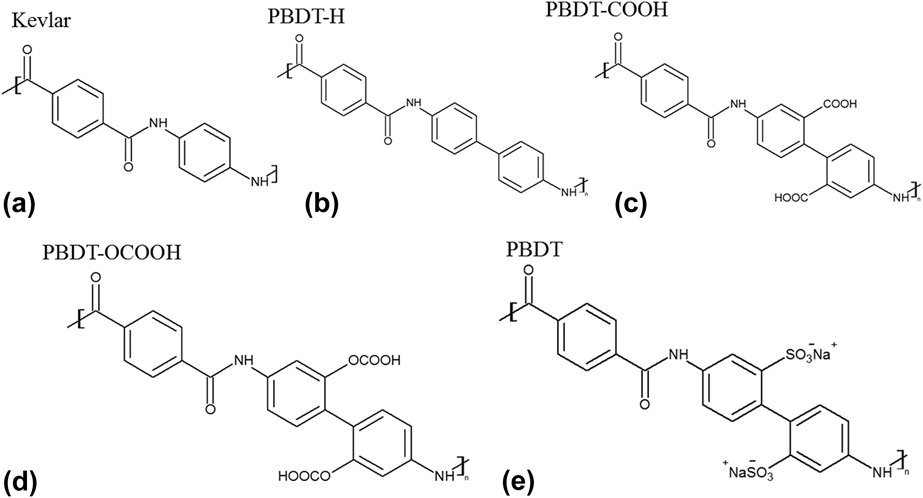
FIG. 1. Chemical structures of five polymers: (a) Kevlar, (b) PBDT-H, (c) PBDT-COOH, (d) PBDT-OCOOH, and (e) PBDT. Note that PBDT-H contains one more phenyl ring than Kevlar in the unit cell, and PBDT-H, PBDT-COOH and PBDT-OCOOH have similar structures with PBDT except functional groups at phenyl rings.
TABLE I. The size of unit cell for unstretched and stretched single-chain polymers, stretch ratio and size of supercells.

The spectral energy density (SED) method was used to calculate phonon dispersions of all the structures.Reference Babaei and Wilmer30–Reference Qian, Gu and Yang33 SED is defined by
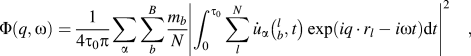 $$\Phi \left( {q,\omega } \right) = {1 \over {4{\tau _0}\pi }}\sum\limits_\alpha {\sum\limits_b^B {{{{m_b}} \over N}} } {\left| {\int_0^{{\tau _0}} {\sum\limits_l^N {{{\dot{u}}_\alpha }} } \left( {_b^l,t} \right)\exp \left( {i{q\,\cdot\,}{r_l} - i\omega t} \right){\rm{d}}t} \right|^2}\quad ,$$
$$\Phi \left( {q,\omega } \right) = {1 \over {4{\tau _0}\pi }}\sum\limits_\alpha {\sum\limits_b^B {{{{m_b}} \over N}} } {\left| {\int_0^{{\tau _0}} {\sum\limits_l^N {{{\dot{u}}_\alpha }} } \left( {_b^l,t} \right)\exp \left( {i{q\,\cdot\,}{r_l} - i\omega t} \right){\rm{d}}t} \right|^2}\quad ,$$where q is the wave vector, ω is the wave frequency, α represents the integration directions (x, y, z), τ0 is the integration time, N is the total number of unit cells in the simulated supercell, B is the total number of atoms in a unit cell, m b is the mass of atom b in the unit cell, ![]() ${\dot{u}_\alpha }\left( {_b^l,t} \right)$ is the α-th component of the velocity of atom b in cell l, and r l is the equilibrium positon of cell l. Note that only backbone atoms of single-chain polymers were used to calculate phonon dispersions because backbone atoms are major contributors to heat conduction along the chain direction, and the effects of the sidechain atoms on thermal conductivity can be reflected in the backbone atoms. Also, if we included sidechain atoms, there would be too many phonon branches and it would become difficult to have a clear picture of the dispersions. The total number of unit cells, N, was set to be 60 along the x direction. Atomic velocities of all backbone atoms were collected every 5 fs during an NVE ensemble for 80 ps. The phonon dispersion along the x direction at 300 K was calculated by the 2D Fourier transform of each
${\dot{u}_\alpha }\left( {_b^l,t} \right)$ is the α-th component of the velocity of atom b in cell l, and r l is the equilibrium positon of cell l. Note that only backbone atoms of single-chain polymers were used to calculate phonon dispersions because backbone atoms are major contributors to heat conduction along the chain direction, and the effects of the sidechain atoms on thermal conductivity can be reflected in the backbone atoms. Also, if we included sidechain atoms, there would be too many phonon branches and it would become difficult to have a clear picture of the dispersions. The total number of unit cells, N, was set to be 60 along the x direction. Atomic velocities of all backbone atoms were collected every 5 fs during an NVE ensemble for 80 ps. The phonon dispersion along the x direction at 300 K was calculated by the 2D Fourier transform of each ![]() ${\dot{u}_\alpha }$ and r l combination as shown in Eq. (2).
${\dot{u}_\alpha }$ and r l combination as shown in Eq. (2).
III. RESULTS AND DISCUSSION
A. Thermal conductivity of unstretched and stretched single-chain polymers
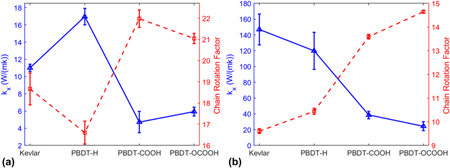
We first obtained k x of unstretched and stretched single-chain polymers. As shown in Fig. 2, all the stretched single-chain polymers show much larger k x than their unstretched counterparts, consistent with stretched PE chainReference He, Kim, Wang and Liu34 and bulk epoxy resinReference Li, Yu, Bao and Yang35 vs. the unstretched ones. We found that k x of stretched Kevlar can be as high as 147.99 ± 19.62 W/(mK) at 300 K, which is larger than the thermal conductivity of more than half of metals. Unstretched Kevlar shows a much smaller k x of 11.01 ± 0.43 W/(mK), although it is larger than the reported thermal conductivity of 3.20 W/(mK) for Kevlar fibersReference Wang, Ho, Segalman and Cahill13 and 8.05 W/(mK) for crystalline KevlarReference Zhang, Wu and Luo14 due to the absence of chain–chain scattering in single-chain Kevlar. k x of stretched Kevlar is larger than that of stretched PBDT-derivative polymers. However, k x of unstretched Kevlar is smaller than that of unstretched PBDT-H. PBDT-H gives larger k x than PBDT-COOH and PBDT-OCOOH for both unstretched and stretched chains due to the absence of functional groups (–COOH and –OCOOH) at phenyl rings.
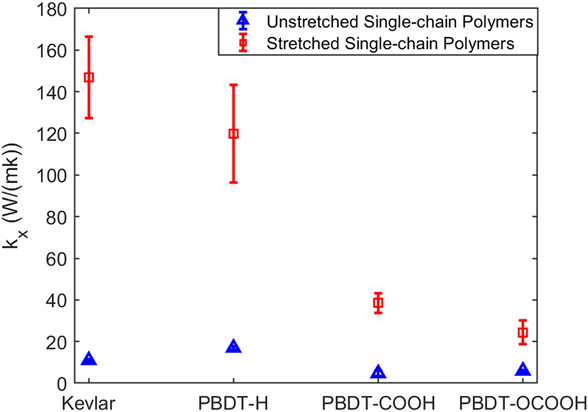
FIG. 2. The comparison of k x for four types of polymers with unstretched or stretched single chains at 300 K.
B. Chain rotation effects on thermal conductivity
Why does the thermal conductivity vary so much among polymer chains of similar structures? To answer this question, we first checked the structures during MD simulations using visual molecular dynamics (VMD).Reference Humphrey, Dalke and Schulten36 It is clear that these single-chain polymers show very different chain rotation level despite small structure differences, as shown in Fig. 4. In general, stretched single-chain polymers are less rotated than their unstretched counterparts because the stretching forces along the chain direction decrease the freedom of the atomic vibration and limit the chain rotation. In both stretched and unstretched cases, PBDT-COOH and PBDT-OCOOH are more rotated than PBDT-H because the existence of functional groups (–COOH or –OCOOH) at phenyl rings makes the rings asymmetric with the tendency to rotate.
To quantify the chain rotation level, we defined a new CRF for a given aligned single-chain polymer along the x direction by the following equation:
where (y, z) are the y- and z-Cartesian coordinates of atoms in a given single polymer chain along x-axis; i denotes the ith snapshot from the atomic position file; N is the total number of snapshots of atomic positions; PDE(y, z) denotes the probability density estimate for each atom (y, z) based on Kernel density estimator,Reference Peter D37 which is a nonparametric way to estimate the probability of having an atom at (y, z). PDE(y, z) was calculated by normal Kernel smoothing function in MATLAB. ![]() $\overline {{\rm{PDE}}\left( {y,z} \right)}$ is the averaged PDE of atoms of interest. In this study, we obtained atomic position files with total snapshots of N = 10 during an NVE ensemble in EMD simulations. We showed an example of PDE for atom (y, z) coordinates of stretched Kevlar in Fig. 3. To consider the aromatic ring rotations in the backbone, we set the area of interest to be the red dashed square in Fig. 3 (5.88 Å2), which is close to the area of a benzene ring of 5.09 Å2. Therefore, the red dashed square contains mostly backbone atoms.
$\overline {{\rm{PDE}}\left( {y,z} \right)}$ is the averaged PDE of atoms of interest. In this study, we obtained atomic position files with total snapshots of N = 10 during an NVE ensemble in EMD simulations. We showed an example of PDE for atom (y, z) coordinates of stretched Kevlar in Fig. 3. To consider the aromatic ring rotations in the backbone, we set the area of interest to be the red dashed square in Fig. 3 (5.88 Å2), which is close to the area of a benzene ring of 5.09 Å2. Therefore, the red dashed square contains mostly backbone atoms. ![]() $\overline {{\rm{PDE}}\left( {y,z} \right)}$ represents the averaged overlap level of (y, z) coordinates in this region. Imagining that there is no chain rotation and all the atoms are in one plane, the (y, z) coordinates of atoms in the red dashed square are highly overlapped, which results in the largest
$\overline {{\rm{PDE}}\left( {y,z} \right)}$ represents the averaged overlap level of (y, z) coordinates in this region. Imagining that there is no chain rotation and all the atoms are in one plane, the (y, z) coordinates of atoms in the red dashed square are highly overlapped, which results in the largest ![]() $\overline {{\rm{PDE}}\left( {y,z} \right)}$ and thus the smallest CRF. However, if this polymer chain rotates, the overlap level of (y, z) coordinates of atoms decreases, leading to reduced
$\overline {{\rm{PDE}}\left( {y,z} \right)}$ and thus the smallest CRF. However, if this polymer chain rotates, the overlap level of (y, z) coordinates of atoms decreases, leading to reduced ![]() $\overline {{\rm{PDE}}\left( {y,z} \right)}$ and thus increased CRF. In brief, larger chain rotation corresponds to less overlap of (y, z) coordinates of atoms and larger CRF. This new CRF is a convenient parameter to characterize the rotation level of aligned single-chain polymers. Compared to the orientational parameter P 2rot, which demands the tedious calculation of the normal vectors of all the planar aromatic rings,Reference Liu and Yang15 the CRF introduced here offers a simple way to quantify chain rotation because the atomic position of all the atoms can be directly recorded in LAMMPS. We expect this parameter to be widely adopted to characterize the rotation levels of aligned polymer chains.
$\overline {{\rm{PDE}}\left( {y,z} \right)}$ and thus increased CRF. In brief, larger chain rotation corresponds to less overlap of (y, z) coordinates of atoms and larger CRF. This new CRF is a convenient parameter to characterize the rotation level of aligned single-chain polymers. Compared to the orientational parameter P 2rot, which demands the tedious calculation of the normal vectors of all the planar aromatic rings,Reference Liu and Yang15 the CRF introduced here offers a simple way to quantify chain rotation because the atomic position of all the atoms can be directly recorded in LAMMPS. We expect this parameter to be widely adopted to characterize the rotation levels of aligned polymer chains.
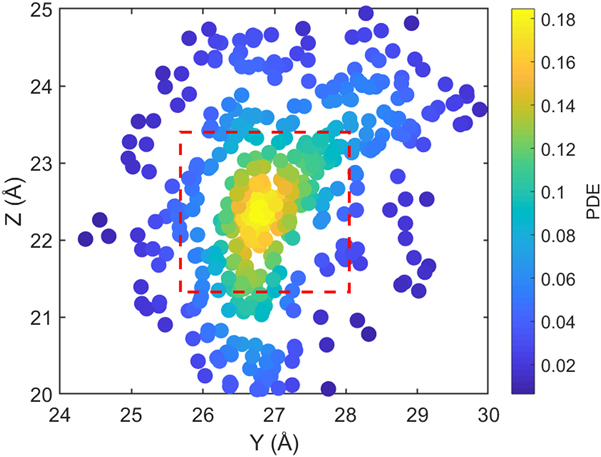
FIG. 3. The scatter plot for Cartesian coordinate points (y, z) of all 448 atoms of a stretched Kevlar. Each atom is colored by the probability density estimate (PDE) based on Kernel density estimator. Larger PDE in the color bar represents a larger overlap level of atoms when projecting onto the y–z plane. ![]() $\overline {{\rm{PDE}}\left( {y,z} \right)}$ was calculated by averaging over all the atoms within the red dashed square, which contains mostly backbone atoms.
$\overline {{\rm{PDE}}\left( {y,z} \right)}$ was calculated by averaging over all the atoms within the red dashed square, which contains mostly backbone atoms.
To show the validity of CRF, we averaged over 10 identical simulations with different random initial velocities for each polymer and included CRF along with the VMD figures of all single-chain polymers in Fig. 4. The structures of single-chain polymers in Fig. 4 directly demonstrate that a more rotated structure has a higher CRF. This supports that CRF is a suitable parameter to characterize chain rotation level. Stretched Kevlar, which is least rotated among these polymers, gives the smallest CRF and the highest thermal conductivity.
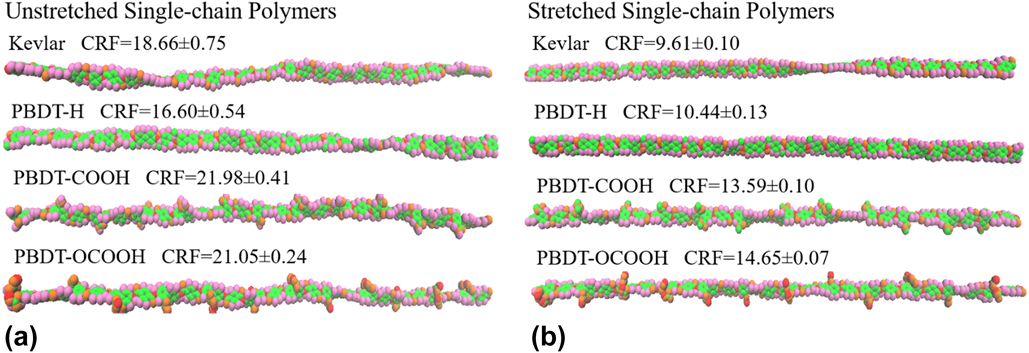
FIG. 4. Snapshots of single-chain polymers from VMD during MD simulation at 300 K and their corresponding CRF: (a) unstretched single-chain polymers and (b) stretched single-chain polymers.
We showed the relationship between k x and CRF of unstretched and stretched single-chain polymers in Figs. 5(a) and 5(b), respectively. k x and CRF are inversely related, no matter they are stretched or unstretched. It reiterates that chain rotation is one decisive factor on thermal conductivity of single-chain polymers.
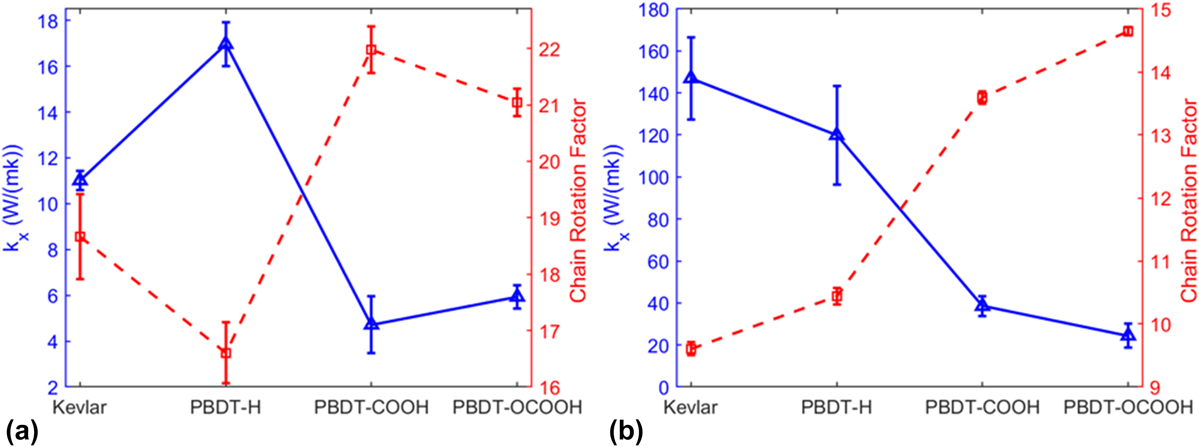
FIG. 5. Thermal conductivity (k x) and CRF of (a) unstretched single-chain polymers and (b) stretched single-chain polymers at 300 K.
C. Phonon dispersion properties of single-chain polymers
Why would large chain rotation lead to low thermal conductivity? To provide deep insights into rotation effects on k x of single-chain polymers, we calculated phonon dispersion by the SED method. The results are shown in Figs. 6(a) and 6(b). Since acoustic modes are dominant heat carriers in thermal transport, we only show phonon modes up to a frequency range of 10 THz. If we take a look at Kevlar first, phonon branches of unstretched Kevlar are more blurred and linewidths are more broadened than stretched Kevlar, indicating smaller phonon lifetimes of unstretched case.Reference Qian, Gu and Yang33,Reference Falkovsky38 This can be understood by that rotational disorder disturbs the heat conduction paths and causes more phonon–phonon scatterings. Moreover, the transverse acoustic (TA) modes of unstretched Kevlar is significantly suppressed from ∼2 THz in the stretched Kevlar to below ∼1 THz. Phonon group velocities in unstretched Kevlar are, thus, lower than those in stretched Kevlar. Because phonon mean free path is a product of phonon lifetime and phonon group velocity, smaller phonon lifetimes and lower phonon group velocities result in smaller phonon mean free paths. With similar heat capacities, lower phonon group velocities and smaller mean free path in unstretched Kevlar leads to smaller k x than stretched Kevlar. Similarly, for PBDT-derivatives, all the phonon branches of unstretched single-chain polymers are blurred with broad linewidth compared to stretched ones, which gives smaller phonon lifetimes for unstretched chains. Meanwhile, TA modes of unstretched single-chain polymers are all suppressed, indicating smaller phonon group velocities. Moreover, if comparing three PBDT-derivatives, we can find both LA and TA modes of PBDT-H have higher frequencies than PBDT-COOH and PBDT-OCOOH in both unstretched and stretched cases, which means larger group velocity for PBDT-H. PBDT-H also shows cleaner phonon curves and narrower linewidth than PBDT-COOH and PBDT-OCOOH, indicating larger phonon lifetimes. Therefore, PBDT-H has higher thermal conductivity than PBDT-COOH and PBDT-OCOOH in both stretched and unstretched cases. In other words, functional groups at phenyl rings in PBDT-COOH and PBDT-OCOOH can significantly suppress acoustic phonon modes and lead to more scatterings, which are essential to reduce their thermal conductivities.
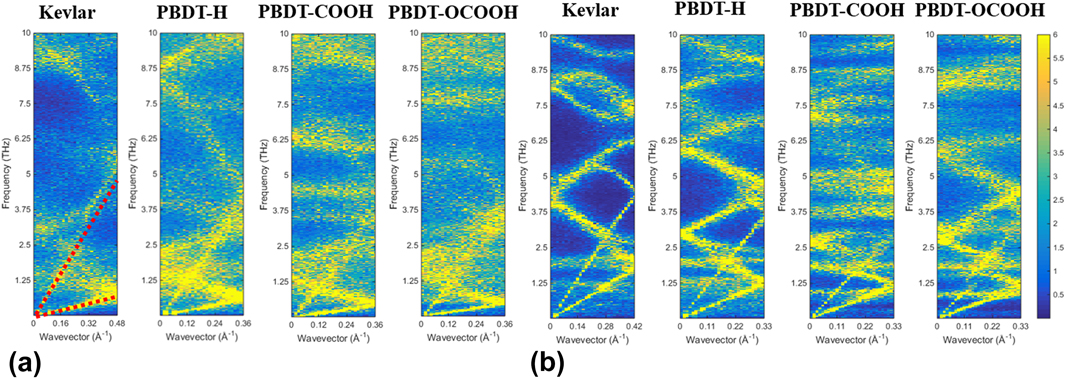
FIG. 6. Phonon dispersion along polymer chains (x direction) calculated by the SED method: (a) unstretched single-chain polymers and (b) stretched single-chain polymers.
If we quantitatively analyze the thermal conductivity of single-chain polymers, k can be estimated by
where k x denotes the thermal conductivity along polymer chains (x direction), c v is the volumetric heat capacity, ![]() ${\bar{v}_x}$ is the average phonon group velocity along polymer chains, and
${\bar{v}_x}$ is the average phonon group velocity along polymer chains, and ![]() ${\bar{l}_x}$ is the average phonon mean free path along polymer chains. Note that because we do not have a complete set of mode-dependent phonon lifetimes and mean free paths in the first Brillouin zone, we can only estimate the average group velocities and average phonon mean free paths. Because our EMD simulations fall into the classical limit, the total volumetric heat capacity can be calculated by c v = 3k BN/V, where k B is the Boltzmann constant, N is the number of atoms, and V is the volume. Acoustic phonon group velocities can be extracted based on the slope from phonon dispersions. Here we assumed linear phonon dispersion of acoustic modes and the phonon group velocity was estimated using the frequency difference between Γ point and the point at zone boundary divided by the length of the wavevector at the zone boundary. [See the red dashed line in Kevlar of Fig. 6(a), for example]. The average phonon group velocity
${\bar{l}_x}$ is the average phonon mean free path along polymer chains. Note that because we do not have a complete set of mode-dependent phonon lifetimes and mean free paths in the first Brillouin zone, we can only estimate the average group velocities and average phonon mean free paths. Because our EMD simulations fall into the classical limit, the total volumetric heat capacity can be calculated by c v = 3k BN/V, where k B is the Boltzmann constant, N is the number of atoms, and V is the volume. Acoustic phonon group velocities can be extracted based on the slope from phonon dispersions. Here we assumed linear phonon dispersion of acoustic modes and the phonon group velocity was estimated using the frequency difference between Γ point and the point at zone boundary divided by the length of the wavevector at the zone boundary. [See the red dashed line in Kevlar of Fig. 6(a), for example]. The average phonon group velocity ![]() $\left( {{{\bar{v}}_x}} \right)$ is calculated by taking the arithmetic mean of all acoustic branches (one LA branch and two TAs). Given k x, c v, and
$\left( {{{\bar{v}}_x}} \right)$ is calculated by taking the arithmetic mean of all acoustic branches (one LA branch and two TAs). Given k x, c v, and ![]() ${\bar{v}_x}$, phonon mean free path
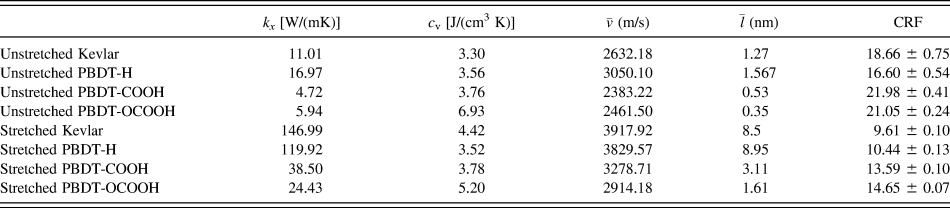
${\bar{v}_x}$, phonon mean free path ![]() $\left( {{{\bar{l}}_x}} \right)$ can be obtained from Eq. (4). All the results are summarized in Table II. Although this is a rough estimation, they can offer valuable insights into the phonon transport in these single-chain polymers. All single-chain polymers have phonon group velocities up to 4000 m/s and the group velocities decrease to below 2500 m/s as the CRF increases. Stretched single-chain polymers show larger phonon group velocities than their corresponding unstretched single-chain polymers. Phonon mean free path of stretched single-chain polymers is more than 4 times larger than unstretched polymers. In other words, phonon mean free path can be significantly increased by stretching polymer chains. Notably, phonon mean free path of PBDT-COOH and PBDT-OCOOH are significantly reduced compared to PBDT-H due to the existence of the functional groups. It highlights the important role of functional groups on chain rotation and, consequently, thermal conductivity.
$\left( {{{\bar{l}}_x}} \right)$ can be obtained from Eq. (4). All the results are summarized in Table II. Although this is a rough estimation, they can offer valuable insights into the phonon transport in these single-chain polymers. All single-chain polymers have phonon group velocities up to 4000 m/s and the group velocities decrease to below 2500 m/s as the CRF increases. Stretched single-chain polymers show larger phonon group velocities than their corresponding unstretched single-chain polymers. Phonon mean free path of stretched single-chain polymers is more than 4 times larger than unstretched polymers. In other words, phonon mean free path can be significantly increased by stretching polymer chains. Notably, phonon mean free path of PBDT-COOH and PBDT-OCOOH are significantly reduced compared to PBDT-H due to the existence of the functional groups. It highlights the important role of functional groups on chain rotation and, consequently, thermal conductivity.
TABLE II. Thermal conductivity (k x), volumetric heat capacity (c v), average phonon group velocity ![]() $\left( {\bar{v}} \right)$, average phonon mean free path
$\left( {\bar{v}} \right)$, average phonon mean free path ![]() $\left( {\bar{l}} \right)$, and CRF of all eight single-chain polymers.
$\left( {\bar{l}} \right)$, and CRF of all eight single-chain polymers.
We also plotted phonon group velocity and phonon mean free path as a function of CRF in Figs. 7(a) and 7(b), respectively, to correlate chain rotation effects with phonon properties. It is shown that both phonon group velocities and mean free paths of single-chain polymers decrease as the CRF increases for both unstretched and stretched single-chain polymers. In other words, chain rotation in single-chain polymers can lead to smaller phonon group velocities and reduced average phonon mean free path by increasing phonon scatterings, resulting in small thermal conductivity.
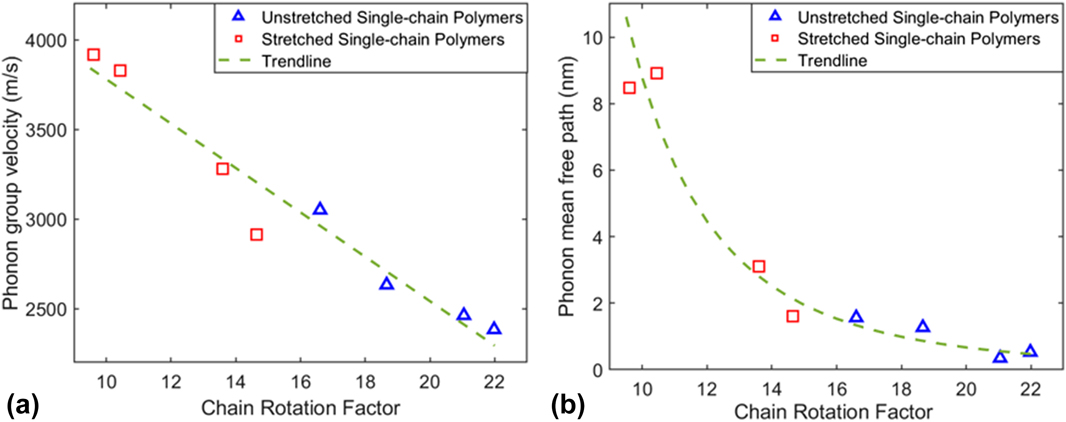
FIG. 7. (a) Phonon group velocities as a function of CRF of single-chain polymers at 300 K. (b) Phonon mean free paths as a function of CRF of single-chain polymers. The green dashed lines denote their decay trend.
IV. SUMMARY
We studied chain rotation effects on thermal conductivity of Kevlar and PBDT-derivatives single-chain polymers using the EMD method. We found that chain rotation plays an essential role in decreasing the thermal conductivity of a given polymer chain from stretched to unstretched or among different polymer chains. Functional groups at phenyl rings in PBDT-derivative single-chain polymers were found to be critical to chain rotation. We introduced a new CRF to quantify aligned single-chain rotation level. We then demonstrated that it is a reliable and convenient parameter to use. We showed that thermal conductivity and CRF are inversely related. We further calculated phonon dispersions of all the polymers and found that large chain rotations cause decreased phonon group velocities and shortened phonon mean free paths, which explains the reduced thermal conductivity. The knowledge obtained in the study provides a deep understanding of how chain rotation reduces thermal conductivity. This can be helpful for guiding the design of polymers with tailored thermal transport properties for a wide array of applications ranging from thermal energy conversion to thermal management of electronics.
ACKNOWLEDGMENTS
This work was funded by NSF CEBT-1641103. Z.T. acknowledges 3M Non-Tenured Faculty Award. This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1053575. The authors also acknowledge Advanced Research Computing at Virginia Tech for providing computational resources and technical support.