I. INTRODUCTION
Recently, there has been growing interest in the possible use of shape memory alloys (SMA) in micro and nanoscale structures and devices, e.g., as sensors or actuators in microelectromechanical systems (MEMS). With a growing worldwide market in excess of 100 billion dollars, MEMS and nanoelectromechanical systems (NEMS) constitute a new paradigm of technological development for the present century and have already found usage as sensors and actuators across numerous industrial sectors.Reference Liu1 The development of multifunctional and smart materialsReference Worden, Bullongh and Hayvood2 is converging with miniaturization technologies, enabling a new generation of smart MEMS (SMEMS). Among the different smart materials targeted for use in SMEMS, SMA have attracted considerable interestReference Kohl3, Reference Bhattacharya and James4 because they offer the highest output work density, about 107 J/m3,Reference Humbeeck5 and exhibit specific desirable thermomechanical effects such as superelasticity and shape memory, due to the reversibility of their thermoelastic martensitic transformation.Reference Otsuka and Wayman6 MEMS components that exhibit superelasticity, one-way or two-way shape memory, could enable a new generation of SMEMS. In addition, the development of more precise and reliable MEMS and NEMS requires improvements in their endurance against hazardous environmental vibrations.Reference Romig, Dugger and McWhorther7–Reference Tanner, Parson, Corwin, Walraven, Wittwer, Boyce and Winzer9 This could be achieved by incorporating high damping materials to suppress vibration noise and impact shocks, and once again SMA are outstanding candidates to play this role due to their high damping properties.Reference San Juan and Nó10
Nevertheless, a fundamental issue concerns the minimum size at which the martensitic transformation can be induced. Several works indicate that in Ti–Ni SMA, the martensitic transformation is suppressed below some critical size, for instance for grains below 60-nm diameterReference Waitz, Kazykhanov and Karnthaler11 and for films of 50-nm thickness,Reference Fu, Zhang, Wu, Huang, Du, Luo, Flewitt and Milne12 and this matter is attracting scientific interest (see Ref.Reference Waitz, Tsuchiya, Antretter and Fischer13 for a recent overview). However, in a different family of SMA based on Cu–Al–Ni, some of the present authors have recently shown using in-situ tests in the transmission electron microscope (TEM)Reference Ibarra, Caillard, San Juan and Nó14–Reference Nó, Ibarra, Caillard and San Juan16 that the thermal or stress-induced martensitic transformation takes place in regions below 50-nm thickness, and the nucleation and growth of martensite variants as small as 20 nm have been observed.
Incorporating SMA into MEMS and NEMS represents a new challenge, and in the last decade, most of the research effort has been focused on the production of shape-memory thin films that could be integrated into the planar technology of Microsystems (see Ref.Reference Miyazaki, Fu and Huang17 for a recent overview). With a view toward reliable devices, the shape memory and superelastic properties should be carefully characterized at the small scales relevant to these applications. One possible approach relies on instrumented nanoindentation techniques (see Refs. Reference Fischer-Cripps18 and Reference Schuh19 for an overview on the technique and its potential applications), which have been successfully applied to SMA both as thin films and bulk materials to characterize their thermomechanical properties and their evolution with thermal treatments.Reference Ni, Cheng and Grummon20–Reference Huang, San Juan and Ramirez39 However, the multiaxial nature of deformation around the nanoindenter renders quantitative interpretation of the data very complex, especially for SMA which exhibit strong nonlinear behavior during thermal- or stress-induced transformation. This difficulty, together with interest in developing three-dimensional SMA devices for MEMS, has moved attention toward the use of nanocompression tests on simple features like micro and nanopillars produced by focused ion beam (FIB) milling. Such pillarsReference Uchic, Dimiduk, Florando and Nix40, Reference Greer, Oliver and Nix41 have been successfully used to study the influence of sample dimensions on crystal plasticity in various metals and alloys and are readily adapted to study the superelastic behavior in SMAs. Indeed, some recently published works have carried out superelastic tests on micro and nanopillars in both Ti–Ni and Cu–Al–Ni SMA families.Reference Frick, Orso and Arzt42–Reference Ye, Mishra, Pelton and Minor47 However, Ti–Ni pillars do not exhibit completely recoverable superelastic behavior, and plastic deformation of the pillars produces a systematic residual deformation.Reference Frick, Orso and Arzt42, Reference Frick, Clark, Orso, Ribic and Arzt44, Reference Norfleet, Sarosi, Manchiraju, Wagner, Uchic, Anderson and Mills45, Reference Ye, Mishra, Pelton and Minor47 A completely recoverable superelastic strain and shape memory in micro and nanopillars was first reported for Cu–Al–Ni SMAs,Reference San Juan, Nó and Schuh43 and also in Cu–Al–Ni SMAs, a size effect on superelastic behavior was recently demonstrated.Reference San Juan, Nó and Schuh46
The above scenario is encouraging for the use of SMA, and in particular the Cu–Al–Ni family, to develop a new generation of SMEMS. The aim of this work is to present an overview of the state-of-the-art of the superelastic and shape memory properties of Cu–Al–Ni pillars at micro and nanoscales. Then, in light of these results, the size effects observed at micro and nanoscales will be discussed in terms of the underlying physical phenomena. Finally a comparative analysis between the observed behavior in Ti–Ni and in Cu–Al–Ni SMA will be presented.
II. EXPERIMENTAL DETAILS
The materials used in this work, as well as in our previous work,Reference San Juan, Nó and Schuh43, Reference San Juan, Nó and Schuh46 are Cu–Al–Ni SMA of several compositions selected to be in the high temperature austenite phase at room temperature (RT) or close to it, according the dependence of the martensitic transformation temperatures on Al and Ni composition.Reference Recarte, Perez-Saez, Bocanegra, Nó and San Juan48, Reference Recarte, Perez-Saez, Bocanegra, Nó and San Juan49 Because of the high elastic anisotropy exhibited by these alloys,Reference Horikawa, Ichinose, Morii, Miyazaki and Otsuka50 the samples used for nanocompression tests are [001] oriented single crystals. Samples were annealed at 1173 K in argon atmosphere for 30 min and quenched in ice-water. In particular, results from three single-crystalline samples will be presented here, with compositions and transformation temperatures (measured by differential scanning calorimetry) given in Table I.
TABLE I. Samples used to machine micropillars and nanopillars by focused ion beam, and further nanocompression testing with a nanoindenter. Sample I, with Af < RT is devoted to superelastic tests. Sample III, with Ms > RT is devoted for shape memory tests. Sample II, with Ms < RT < Af can be used for both kinds of tests, as explained in the text.

A polished [001] surface of a section cut from a single crystal was used to machine micropillars by FIB, at the Center for Nanoscale Systems of Harvard University, with a FEI Dual Beam DB235 (Hillsboro, OR) instrument. The conditions for milling were 30 kV and a sequence of decreasing currents for the different annular milling steps to produce a pillar. The milling procedure has been described in previous works,Reference San Juan, Nó and Schuh43, Reference San Juan, Nó and Schuh46 which also analyze the possible influence of gallium contamination and conclude that it does not fundamentally alter the mechanical behavior of the micro and nanopillars. Figure 1(a) shows a scanning electron micrograph of one typical micropillar at the center of the corresponding crater, which is oversized to facilitate observation and coarse positioning of the nanoindenter tip and to avoid the interaction of the indenter with the crater sides during compression testing.

FIG. 1. (a) Scanning electron micrograph of a typical micropillar in the center of the crater milled by focused ion beam (FIB). (b) Contact-mode topography image acquired with the indenter tip. (c) Image of the top of the micropillar for precise positioning of the indenter before the compression test. (d) Image taken just after a series of compression tests, showing the residual indent.
The nanocompression tests were performed using a Hysitron Triboindenter (Minneapolis, MN) at the Nanomechanical Technology Laboratory at the Massachusetts Institute of Technology, with the following basic procedure. Initially the position of the crater on the sample surface was identified by optical microscopy. Then we used the indenter tip as scanning probe at a fixed contact load of 2 μN to acquire a contact-mode topography image of the crater during a 30×30 μm scan, as shown in Fig. 1(b). Because we used a spheroconical diamond indenter tip of 0.6-μm radius, the contact-mode image presents a convolution of the surface and tip, with imaging resolution limited by the shape of the tip. However, the location of the pillar (and importantly, the center of the pillar) is still easily identified through a higher magnification scan of 3×3 μm, Fig. 1(c). By using this procedure, the indenter can be precisely positioned with respect the pillar axis, which is crucial to ensure on-axis loading for superelastic compression tests. Indeed, the position of the indent produced in the micropillars during the local deformation around the settling point can be clearly observed in Fig. 1(d). Last, the piezoelectric control of the tip also allows a controlled lateral displacement of the indenter tip to carry out off-axis loading to induce bending of the pillars, for shape memory tests.
III. EXPERIMENTAL RESULTS AND DISCUSSION
A. Superelastic behavior
Nanocompression tests to study the superelastic effect were performed on numerous pillars of various sizes, machined by FIB from the samples described above. The pillars were in general milled with an aspect ratio near three as recommended for microcompression tests.Reference Zhang, Schuster, Wei and Ramesh51 In what follows we will present the general approach to these studies, giving some selected examples and establishing their relationship with previous work.
We first describe the superelastic tests performed on Sample I. Figure 2(a) shows the load–displacement curves obtained on one of the micropillars machined by FIB, with 5.3-μm height and a mean diameter of 1.6 μm. After carefully positioning the apex of the indenter over the pillar, we carried out a multiple-cycle compression test: two cycles were applied with a maximum load of 200 μN, followed by two cycles at 350 μN, and last two at 500 μN. The load versus displacement curves from these tests are plotted in Fig. 2(a), in which we show for clarity only cycles 1, 3, 5, and 6. In our previous work on similar micro pillars,Reference San Juan, Nó and Schuh43 we performed some tests on other different pillars machined from the same sample, and we described what happens during the first loading cycles at increasing loads; the behavior shown in Fig. 2 is quite similar. When the load reaches a critical value of about 310–340 μN, a sudden strain plateau occurs and more than 200-nm displacement accumulates with relatively little increase of the load; this is the superelastic effect in which the stress-induced martensitic transformation is triggered for a critical stress according the Clausius–Clapeyron equation.Reference Otsuka and Wayman6 The load–displacement curve shows step-like behavior due to the fast nucleation and growth of martensite variants under stress. The total displacement corresponds to several percent strain of the pillar, as shown in Ref. Reference San Juan, Nó and Schuh43, and for comparison we note that the pop-in events due to dislocation motion during incipient plasticity usually have a much smaller depth of only some few nanometers.Reference Schuh, Mason and Lund52 During unloading, martensite becomes unstable (with some stress hysteresis) and the reverse martensitic transformation takes place with recovery of the displacement.

FIG. 2. (a) The first few cycles of compression on a pillar of 1.6-μm diameter milled from Sample I, showing superelastic behavior and the small residual deformation linked to the local plastic deformation under the indenter tip. (b) Enlarged area to appreciate the residual displacement during the cycles, which become nearly closed when the maximum load is not increased. In both cases, the number of each cycle has been labeled.
However, during the first compression cycles at increasing load, some residual displacement can be observed as a consequence of the local plastic deformation due to settling at the contact point of the indenter, as can be clearly appreciated on the enlarged area of Fig. 2(b). In this particular case, the accumulated residual displacement is about 30 nm, but this is dependent on the size of the pillar, being typically below 70 nm for micropillars with less than 2-μm diameter. As we showed in,Reference San Juan, Nó and Schuh43 this residual deformation is associated with the indentation that is present on the top of the pillar after the tests, as shown for example in Fig. 1(d) for comparison with the image before the tests. When the applied load is not increased further, the cycle becomes fully closed, as can be seen in Fig. 3(a), which corresponds to a new cycle after those from Fig. 2. Then we observe a completely recoverable superelastic effect.

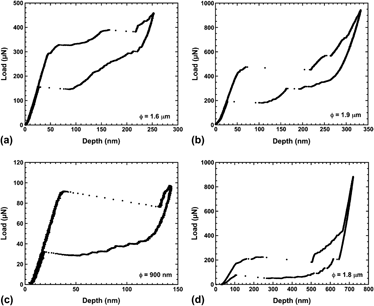
FIG. 3. Examples of completely reversible superelastic behavior in Cu–Al–Ni shape memory alloys. (a) Pillar of 1.6-μm diameter on Sample I. (b) Pillar of 1.9-μm mean diameter on Sample I. (c) Pillar of 900-nm diameter on Sample II. (d) Pillar of 1.8-μm mean diameter on Sample II. For an easy identification, the pillar diameter ϕ has been indicated in each picture.
Once the indenter tip has settled into the top of the pillar, the tip shape is accommodated, and during subsequent loading, the micropillar experiences essentially uniform compressive load. Then the micropillars undergo completely reversible superelastic straining, which becomes perfectly reproducible over many cycles. The superelastic behavior obtained after the initial settling stage is shown in Fig. 3 for several different pillars machined in Samples I and II. As noted before, Fig. 3(a) corresponds to the same pillar in Sample I shown in Fig. 2. On the same sample, but in another pillar of slightly higher diameter, the superelastic curve of Fig. 3(b), shows a higher critical load. Through the height and diameter of the pillars, the load–displacement curves can be converted into stress–strain curves.Reference San Juan, Nó and Schuh43 However, the taper often exhibited by the smaller FIBed pillars is a source of error, and for this reason the raw load–displacement data are presented in this work.
Figure 3(c) shows similar superelastic behavior in a submicrometer pillar with a mean diameter of 900 nm, milled in Sample II. The superelastic tests on this pillar do not leave any residual indentation after a series of many cyclesReference San Juan, Nó and Schuh46 and exhibit a clear size effect that will be discussed later. Last, Fig. 3(d) shows the superelastic cycle on a larger pillar of 1.8-μm mean diameter, milled in Sample II. In this case, the superelastic strain reaches the maximum theoretical strain in compression for martensite, which becomes completely reoriented by the shear stress and then is elastically deformed. The elastic recovery is clearly evidenced during unloading and subsequently the reverse stress-induced transformation also exhibits perfect strain recovery and demonstrates the superelastic effect.
B. Shape memory behavior
To test the shape memory behavior we used Samples II and III. According to the data in Table I, at RT Sample II can be in austenite or partially in martensite depending on whether it has been cooled or heated previously, while Sample III should be always partially in martensite at RT. However, due to the size effects reported in,Reference San Juan, Nó and Schuh46 the pillars become thermally more stable and the thermal martensitic transformation is shifted to lower temperatures than in the bulk material. As a consequence, at RT, pillars in these samples can undergo superelastic deformation, at least during the first cycle. However, once the martensite is induced by the applied stress it is stable, so the reverse transformation does not take place and the pillar remains deformed and in the martensitic phase. During subsequent heating the pillar recovers its undeformed straight shape by the one-way shape memory effect. This shape memory behavior in micro and nanopillars was first reported and explained inReference San Juan, Nó and Schuh43 for some pillars milled in Sample II. Here we will illustrate that the phenomena is reproducible; the same kind of behavior takes place in pillars from Sample III.
In Fig. 4(a), the first compression cycles on a pillar with a mean diameter of 1.8 μm milled from Sample III are shown. At a critical load of about 260 μN, the stress-induced martensitic transformation takes place and produces a large stepped plateau, and later the martensite becomes completely oriented as evidenced by the elastic recovery during unloading. However, now the martensite is nearly stable and only a small recovery is observed. The main part of the reverse transformation does not take place and consequently a large residual deformation of about 530 nm can be observed. Obviously, as it is the first cycle, this residual depth must include the local plastic deformation produced beneath the indent, but all of our data on the indent formation described earlier suggest that this displacement would be irrelevant in comparison to the full amount seen here, which is mostly associated with the martensitic transformation. Subsequently, during a new cycle the pillar is almost completely in martensite, which deforms and recovers elastically with only a very small closed cycle due to the small amount of martensite transforming back.

FIG. 4. (a) Compression test and stress-induced martensitic transformation in a pillar of Sample III, which becomes stable in the martensite phase. (b) Micrograph of the micropillar before the off-axis test. (c) Image of the same pillar deformed by bending just after the off-axis test. (d) Image of the pillar after heating, showing recovery by the one-way shape memory effect.
It is difficult to study further recovery of this specimen by heating while under load during a compression test. So instead we developed a new kind of “off-axis” compression test. In these tests, the compression load is applied somewhat off-center of the pillar to produce a lateral bending force. In this configuration, the apex of the indenter glides off of the top of the pillar and the load is applied through the inclined faces of the indenter in contact with the pillar. Although the edge of the pillar is slightly damaged, the main deformation induced by this procedure is a bending of the micropillar to one side. Figure 4(b) shows the image of the pillar before the off-axis compression test, and Fig. 4(c) shows the same pillar just after the compression test. We may note some contamination and/or distortion on the top and side of the micropillar because of the compression tests and sample handling between indenter and microscope. Once the pillar is bent, it remains deformed because it is in the martensite phase, as shown in Fig. 4(c). When the sample was moderately heated to above Af and observed again in the scanning electron microscope, the postheating micrograph shown in Fig. 4(d) shows the complete recovery of the pillar by the one-way shape memory effect. During this recovery, forces equivalent to the stress-induced recovery plateau at the reverse transformation temperatures, i.e., forces of several hundred μN, are expected to be developed, paving the way to design microdevices for actuation or manipulation operations.
C. Size effects at the nanoscale
In previous work,Reference San Juan, Nó and Schuh46 we reported a size effect on the superelastic behavior in submicrometer pillars in which the austenite becomes stable up to much higher stresses than in bulk material, and once the pillar is transformed by the superelastic effect, the stress-induced martensite becomes more stable than in bulk materials, delaying the reverse transformation. As a consequence, the stress–strain cycle during superelastic deflection enclosed a much larger area (corresponding to the dissipated mechanical energy), and such nanopillars exhibit an ultrahigh damping coefficient with a merit index for structural damping higher than any other material. This behavior is illustrated in Fig. 5, where the stress–strain curve of a 900-nm diameter nanopillar is compared with the ones obtained for the bulk single crystals of exactly the same material at different temperatures.Reference San Juan, Nó and Schuh46, Reference Ibarra, San Juan, Bocanegra and Nó53 The nanocompression tests were performed at RT, and for the nanopillar, one would expect a critical stress below that measured at 305 K, according the Clausius–Clapeyron equation. On the contrary, the critical stress as well as the enclosed area of the cycle are much higher for the nanopillar than the expected normal behavior and can be attributed to a size effect, which will be discussed in the following.

FIG. 5. Comparison of the compression stress–strain curves of a 900-nm-diameter pillar and the ones obtained on the same bulk single crystal from which the pillar has been FIBed. This picture evidence the size effect on the mechanical behavior at nanoscale because, according the Clausius–Clapeyron equation, the curve of the pillar should be below the one at 305 K.
The explanation for the stabilization of austenite could lie in a geometrical size effect: in such small pillars there is a paucity of nucleation points for martensite, which usually lie at grain boundaries, other microstructural features, or stress-concentrating surface defects. Since we work with single crystals there is no microstructure per se, and the surface of the FIBed pillars is smooth and free of stress-concentrating potential nucleation sites. In bulk alloys, martensite is also known to nucleate on dislocation cores,Reference Ibarra, Caillard, San Juan and Nó14, Reference Nó, Ibarra, Caillard and San Juan15 but the density of dislocations in our single crystals is very low. Thus, upon loading of a submicrometer pillar, there are few low-stress nucleation sites for martensite, and thus, much higher stresses are achieved before the forward transformation begins. In addition, due to the size of the pillar, the required force was only about 95 μN, like in Fig. 3(c), and it was not enough to reach the yield point for plastic deformation of the austenite beneath the indenter. On the contrary, in previous resultsReference San Juan, Nó and Schuh43 as the pillars were larger, the required force was above 250 μN, and then the stress beneath the indenter was high enough to produce local plastic deformation before reaching the critical stress to trigger the transformation, as in Figs. 2 and 1(d). So locally at the contact point many dislocations were created, offering easy nucleation points for further stress-induced transformation. This can explain why the critical stress observed inReference San Juan, Nó and Schuh43 was similar to that in bulk single crystals and no size effect was observed in the transformation stress. Then, the observed size effect during the stress-induced forward transformation can be plausibly ascribed to the transition from a low-stress heterogeneous nucleation mechanism in bulk materials, to a higher-stress nucleation at less preferred sites in nano and submicrometer pillars.
There is also another potential contribution to the size effect, associated with the transformation stress distribution in small samples. In bulk materials during the forward martensitic transformation (thermal- or stress-induced), elastic energy is stored associated with shape and volume accommodation between the phases around the multiple interfaces. In macroscopic samples, this stored elastic energy is known to promote the reverse transformation when the stress is withdrawn.Reference Otsuka and Wayman6 Nevertheless, in nano and micrometer pillars the martensite variants can span the entire pillar, relieving the stored elastic energy at the surface and improving their stability, which could affect the stresses at which the reverse transformation happens. This interpretation agrees with the delay of the reverse thermal martensitic transformation, recently measured by adiabatic calorimetry, when the elastic stresses are released.Reference Rodriguez-Aseguinolaza, Ruiz-Larrea, Nó, Lopez-Echarri and San Juan54, Reference Rodriguez-Aseguinolaza, Ruiz-Larrea, Nó, Lopez-Echarri and San Juan55 A recent report on size effects in SMA microwires with a bamboo microstructureReference Chen and Schuh56 also considered this effect, and with finite element modeling established that the relaxation of transformation stresses at free surfaces can indeed be expected to contribute to a shift in the critical stress or temperature for transformation.
IV. FINAL DISCUSSION AND CONCLUSIONS
The above results show the complete recovery and very good reproducibility of superelastic behavior in micro and nanopillars of Cu–Al–Ni SMA and the one-way shape memory effect exhibited by these small structures. What is more, in a recent work,Reference San Juan, Nó and Schuh57 we showed that superelastic cycling in such Cu–Al–Ni micropillars is reproducible with complete recovery over hundreds of cycles. In light of these results, we may ask why similar behavior is not observed in micropillars of Ti–Ni SMA, which show little to no recoverable superelasticity at the finest scales?
We will focus our final discussion on this question. The first study on Ti–Ni pillars,Reference Frick, Orso and Arzt42 from 2-μm to 170-nm diameter, with [111] compression axis orientation, reported a loss of superelasticity in all cases, and the pillars instead deformed plastically. This loss of superelasticity in micro and nanopillars was confirmed to be independent of the single crystal orientation.Reference Frick, Clark, Orso, Ribic and Arzt44 In another recent workReference Norfleet, Sarosi, Manchiraju, Wagner, Uchic, Anderson and Mills45 on larger Ti-Ni [110] oriented micropillars, from 5- to 20-μm diameter, the superelastic strain was observed and even recovered nearly completely for the first two cycles, although for further cycles the pillars were plastically deformed, with the generation of a high density of entangled dislocations.
In light of the above interpretation of the size effects in our samples, we may speculate that the loss of pseudoelasticity in Ti–Ni reported inReference Frick, Orso and Arzt42 andReference Frick, Clark, Orso, Ribic and Arzt44 could be related to the higher critical stress in Ti–Ni (in comparison with Cu–Al–Ni), which would promote local plastic deformation of the pillars (e.g., at the contact point) before reaching the stress required to trigger the transformation. On the other hand, the effect could be chemical in origin. It is well known that Ti–Ni SMAs are spontaneously and very quickly covered by a thin film of TiO2. Ishida and SatoReference Ishida and Sato58 studied the influence of the oxide film formation on Ti–Ni thin films, and even for low-temperature treatments in high vacuum, an oxide film of 7 nm was formed on the surface of the Ti–Ni thin films, giving rise to a Ti-depleted zone about 50-nm thick beneath the Ti-rich oxide film. This composition shift of the depleted zone lowers the transformation temperatures, and taking into account the narrow superelastic window of Ti–Ni, it is expected that this depleted layer will not transform under stress. These results were confirmed in further work on Ti–Ni thin films,Reference Fu, Zhang, Wu, Huang, Du, Luo, Flewitt and Milne12 where an even thicker titanium oxide layer (TiO2+TiOx) of about 25 nm was reported.
Then, keeping in mind the described influence of the surface oxide film, we may consider the micro and nanopillars of Ti–Ni SMA as composite cylinders comprising a cylindrical outer shell of a brittle ceramic material, TiO2, exhibiting high modulus E(TiO2) =2 87 GPa and high compressive strength σy(TiO2)≈ 3 GPa.Reference Carter and Norton59 Beneath the oxide film, the Ti–Ni pillars would have a tubular region of material out of stoichiometry, about 50 nm or thicker, which would not participate in the stress-induced transformation and thus would exhibit a stiff elastic response. During nanocompression tests, both cylindrical regions (oxide + depleted zone) not only will exhibit higher modulus and compressive strength but also will constrain the stress-induced transformation of the normal Ti–Ni material at the pillar core. Then, much higher loads would need to be applied to deform such a composite structure, reaching the stress for plastic deformation of the Ti–Ni inner material and potentially suppressing the superelastic behavior, and in particular superelastic recovery. Obviously, the influence of this surface composite structure would become increasingly dominant for smaller nanopillars and would be less relevant for large diameter pillars. This could explain why in larger pillars of about 20-μm diameter the superelastic behavior is still observed during the first cycles, as in,Reference Norfleet, Sarosi, Manchiraju, Wagner, Uchic, Anderson and Mills45 whereas in pillars below 1 μm it is lost from the very beginning.Reference Frick, Orso and Arzt42 Even more, the above description could offer a very simple explanation for the results reported by Ye et al.Reference Ye, Mishra, Pelton and Minor47; in a 200-nm-diameter Ti–Ni pillar, the load for compression must be very high because the pillar will be strongly influenced by the oxidized outer shell. In fact, an outer shell, about 15 nm or thicker, can be discerned in TEM micrographs of Fig. 2(b) in Ref.Reference Ye, Mishra, Pelton and Minor47 With a rigid oxide shell and Ti-depleted zone in the pillar, the entire structure could act as a rigid punch, transmitting stress from the indenter all the way to the substrate, inducing the stress-induced transformation there rather than in the pillar.
While this mechanism needs to be borne out by more detailed investigation, the phenomenon would be characteristic of Ti–Ni pillars and should not be relevant in Cu–Al–Ni pillars; this stands in contrast to the criticism of Ye et al.Reference Ye, Mishra, Pelton and Minor47 that Cu–Al–Ni pillar compression experimentsReference San Juan, Nó and Schuh46 may involve substrate deformation. We suggest that on the contrary, it may be the chemical constitution of Ti–Ni SMA pillars that lead to such effects via the problems linked with oxide film formation. We find that micro and nanopillars machined from single crystalline Cu–Al–Ni SMA exhibit clean and reproducible superelastic behavior, with complete recovery, as well as one-way shape memory. We hope that this useful behavior can be exploited for microdevices, opening the door for the development of a new generation of SMEMS.
ACKNOWLEDGMENTS
This work was supported by the Spanish Ministry of Science and Innovation (MICINN) project MAT2009-12492 and the CONSOLIDER-INGENIO 2010 CSD2009-00013, by the Consolidated Research Group IT-10-310 from the Education Department and by the project ETORTEK ACTIMAT-08 from the Industry Department of the Basque Government. CS acknowledges support from the U.S. Army Research Office through the Institute for Soldier Nanotechnologies at MIT. This work made use of the Center for Nanscale Systems (CNS) from Harvard University with the support of the National Nanotechnology Infrastructure Network (NNIN).