Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Carlton-Jones, Arthur
Paul, Elizabeth J.
and
Dorland, William
2021.
Computing the shape gradient of stellarator coil complexity with respect to the plasma boundary.
Journal of Plasma Physics,
Vol. 87,
Issue. 2,
Abd Elaziz, Mohamed
Almodfer, Rolla
Ahmadianfar, Iman
Ibrahim, Ibrahim Anwar
Mudhsh, Mohammed
Abualigah, Laith
Lu, Songfeng
Abd El-Latif, Ahmed A.
and
Yousri, Dalia
2022.
Static models for implementing photovoltaic panels characteristics under various environmental conditions using improved gradient-based optimizer.
Sustainable Energy Technologies and Assessments,
Vol. 52,
Issue. ,
p.
102150.
Nies, Richard
Paul, Elizabeth J.
Hudson, Stuart R.
and
Bhattacharjee, Amitava
2022.
Adjoint methods for quasi-symmetry of vacuum fields on a surface.
Journal of Plasma Physics,
Vol. 88,
Issue. 1,
Hegna, C.C.
Anderson, D.T.
Bader, A.
Bechtel, T.A.
Bhattacharjee, A.
Cole, M.
Drevlak, M.
Duff, J.M.
Faber, B.J.
Hudson, S.R.
Kotschenreuther, M.
Kruger, T.G.
Landreman, M.
McKinney, I.J.
Paul, E.
Pueschel, M.J.
Schmitt, J.S.
Terry, P.W.
Ware, A.S.
Zarnstorff, M.
and
Zhu, C.
2022.
Improving the stellarator through advances in plasma theory.
Nuclear Fusion,
Vol. 62,
Issue. 4,
p.
042012.
Joglekar, Archis S.
and
Thomas, Alexander G.R.
2022.
Unsupervised discovery of nonlinear plasma physics using differentiable kinetic simulations.
Journal of Plasma Physics,
Vol. 88,
Issue. 6,
Dudt, D.W.
Conlin, R.
Panici, D.
and
Kolemen, E.
2023.
The DESC stellarator code suite Part 3: Quasi-symmetry optimization.
Journal of Plasma Physics,
Vol. 89,
Issue. 2,
Gaur, Rahul
Buller, Stefan
Ruth, Maximilian E.
Landreman, Matt
Abel, Ian G.
and
Dorland, William D.
2023.
An adjoint-based method for optimising MHD equilibria against the infinite-n, ideal ballooning mode.
Journal of Plasma Physics,
Vol. 89,
Issue. 5,
Merlo, Andrea
Böckenhoff, Daniel
Schilling, Jonathan
Lazerson, Samuel Aaron
and
Pedersen, Thomas Sunn
2023.
Physics-regularized neural network of the ideal-MHD solution operator in Wendelstein 7-X configurations.
Nuclear Fusion,
Vol. 63,
Issue. 6,
p.
066020.
Krüger, Florian
Zhang, Du
Luan, Pingshan
Park, Minjoon
Metz, Andrew
and
Kushner, Mark J.
2024.
Autonomous hybrid optimization of a SiO2 plasma etching mechanism.
Journal of Vacuum Science & Technology A,
Vol. 42,
Issue. 4,
Nies, Richard
Paul, Elizabeth J.
Panici, Dario
Hudson, Stuart R.
and
Bhattacharjee, Amitava
2024.
Exploration of the parameter space of quasisymmetric stellarator vacuum fields through adjoint optimisation.
Journal of Plasma Physics,
Vol. 90,
Issue. 6,
Wei, Wenyin
Hua, Jiankun
Knieps, Alexander
Liu, Shaocheng
and
Liang, Yunfeng
2025.
Deformation of invariant tori under perturbation.
Plasma Physics and Controlled Fusion,
Vol. 67,
Issue. 7,
p.
075006.
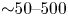 ${\sim }50\text {--}500$) in comparison with a finite-difference gradient-based method. We discuss regularization objectives of relevance for fixed-boundary optimization, including a novel method that prevents self-intersection of the plasma boundary. We present several optimized equilibria, including a vacuum field with very low magnetic shear throughout the volume.
${\sim }50\text {--}500$) in comparison with a finite-difference gradient-based method. We discuss regularization objectives of relevance for fixed-boundary optimization, including a novel method that prevents self-intersection of the plasma boundary. We present several optimized equilibria, including a vacuum field with very low magnetic shear throughout the volume.

