Article contents
Impurity temperature screening in stellarators close to quasisymmetry
Published online by Cambridge University Press: 19 June 2020
Abstract
Impurity temperature screening is a favourable neoclassical phenomenon involving an outward radial flux of impurity ions from the core of fusion devices. Quasisymmetric magnetic fields lead to intrinsically ambipolar neoclassical fluxes that give rise to temperature screening for low enough 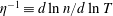 $\unicode[STIX]{x1D702}^{-1}\equiv d\ln n/d\ln T$. In contrast, neoclassical fluxes in generic stellarators will depend on the radial electric field, which is predicted to be inward for ion-root plasmas, potentially leading to impurity accumulation. Here, we examine the impurity particle flux in a number of approximately quasisymmetric stellarator configurations and parameter regimes while varying the amount of symmetry breaking in the magnetic field. For the majority of this work, neoclassical fluxes have been obtained using the SFINCS drift-kinetic equation solver with electrostatic potential
$\unicode[STIX]{x1D702}^{-1}\equiv d\ln n/d\ln T$. In contrast, neoclassical fluxes in generic stellarators will depend on the radial electric field, which is predicted to be inward for ion-root plasmas, potentially leading to impurity accumulation. Here, we examine the impurity particle flux in a number of approximately quasisymmetric stellarator configurations and parameter regimes while varying the amount of symmetry breaking in the magnetic field. For the majority of this work, neoclassical fluxes have been obtained using the SFINCS drift-kinetic equation solver with electrostatic potential 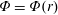 $\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D6F7}(r)$, where
$\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D6F7}(r)$, where  $r$ is a flux-surface label. Results indicate that achieving temperature screening is possible, but unlikely, at low-collisionality reactor-relevant conditions in the core. Thus, the small departures from symmetry in nominally quasisymmetric stellarators are large enough to significantly alter the neoclassical impurity transport. A further look at the magnitude of these fluxes when compared to a gyro-Bohm turbulence estimate suggests that neoclassical fluxes are small in configurations optimized for quasisymmetry when compared to turbulent fluxes.
$r$ is a flux-surface label. Results indicate that achieving temperature screening is possible, but unlikely, at low-collisionality reactor-relevant conditions in the core. Thus, the small departures from symmetry in nominally quasisymmetric stellarators are large enough to significantly alter the neoclassical impurity transport. A further look at the magnitude of these fluxes when compared to a gyro-Bohm turbulence estimate suggests that neoclassical fluxes are small in configurations optimized for quasisymmetry when compared to turbulent fluxes.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 6
- Cited by

