Article contents
Particle acceleration in neutron star ultra-strong electromagnetic fields
Published online by Cambridge University Press: 25 August 2020
Abstract
In this paper, we discuss the results of a new particle pusher in realistic ultra-strong electromagnetic fields such as those encountered around rotating neutron stars. After presenting the results of this algorithm in simple fields and comparing them to expected exact analytical solutions, we present new simulations for a rotating magnetic dipole in vacuum for a millisecond pulsar by using the Deutsch solution. Particles are injected within the magnetosphere, neglecting radiation reaction, interaction among them and their feedback on the fields. Our simulations are therefore not yet fully self-consistent because the Maxwell equations are not solved according to the current produced by these particles. The code highlights the symmetrical behaviour of particles of opposite charge to mass ratio, 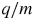 $q/m$, with respect to the north and south hemispheres. The relativistic Lorentz factor
$q/m$, with respect to the north and south hemispheres. The relativistic Lorentz factor 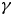 $\gamma$ of the accelerated particles is proportional to this ratio
$\gamma$ of the accelerated particles is proportional to this ratio 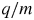 $q/m$: protons reach up to
$q/m$: protons reach up to 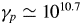 $\gamma _p \simeq 10^{10.7}$, whereas electrons reach up to
$\gamma _p \simeq 10^{10.7}$, whereas electrons reach up to 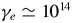 $\gamma _e \simeq 10^{14}$. Our simulations show that particles could either be captured by the neutron star, trapped around it or ejected far from it, well outside the light cylinder. Actually, for a given charge to mass ratio, particles follow similar trajectories. These particle orbits show some depleted directions, especially at high magnetic inclination with respect to the rotation axis for positive charges and at low inclination for negative charges because of symmetry. Other directions are preferred and loaded with a high density of particles, some directions concentrating the highest or lowest acceleration efficiencies.
$\gamma _e \simeq 10^{14}$. Our simulations show that particles could either be captured by the neutron star, trapped around it or ejected far from it, well outside the light cylinder. Actually, for a given charge to mass ratio, particles follow similar trajectories. These particle orbits show some depleted directions, especially at high magnetic inclination with respect to the rotation axis for positive charges and at low inclination for negative charges because of symmetry. Other directions are preferred and loaded with a high density of particles, some directions concentrating the highest or lowest acceleration efficiencies.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2020. Published by Cambridge University Press
References
REFERENCES
- 7
- Cited by

