Article contents
A relativistic particle pusher for ultra-strong electromagnetic fields
Published online by Cambridge University Press: 26 August 2020
Abstract
Kinetic plasma simulations are nowadays commonly used to study a wealth of nonlinear behaviours and properties in laboratory and space plasmas. In particular, in high-energy physics and astrophysics, the plasma usually evolves in ultra-strong electromagnetic fields produced by intense laser beams for the former or by rotating compact objects such as neutron stars and black holes for the latter. In these ultra-strong electromagnetic fields, the gyro-period is several orders of magnitude smaller than the time scale on which we desire to investigate the plasma evolution. Some approximations are required such as, for instance, artificially decreasing the electromagnetic field strength, which is certainly not satisfactory. The main flaw of this downscaling is that it cannot reproduce particle acceleration to ultra-relativistic speeds with a Lorentz factor above 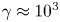 $\gamma \approx 10^3$–
$\gamma \approx 10^3$–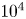 $10^4$. In this paper, we design a new algorithm able to catch particle motion and acceleration to a Lorentz factor of up to
$10^4$. In this paper, we design a new algorithm able to catch particle motion and acceleration to a Lorentz factor of up to 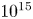 $10^{15}$ or even higher by using Lorentz boosts to special frames where the electric and magnetic field are parallel. Assuming that these fields are locally uniform in space and constant in time, we solve analytically the equation of motion in a tiny region smaller than the length scale of the spatial and temporal gradient of the field. This analytical integration of the orbit severely reduces the constraint on the time step, allowing us to use large time steps, avoiding resolving the ultra-high gyro-frequency. We performed simulations in ultra-strong spatially and time-dependent electromagnetic fields, showing that our particle pusher is able to follow accurately the exact analytical solution for very long times. This property is crucial to properly capture for instance lepton electrodynamics in electromagnetic waves produced by fast rotating neutron stars. We conclude with a simple implementation of our new pusher into a one-dimensional relativistic electromagnetic particle-in-cell code, testing it against plasma oscillations, two-stream instabilities and strongly magnetized relativistic shocks.
$10^{15}$ or even higher by using Lorentz boosts to special frames where the electric and magnetic field are parallel. Assuming that these fields are locally uniform in space and constant in time, we solve analytically the equation of motion in a tiny region smaller than the length scale of the spatial and temporal gradient of the field. This analytical integration of the orbit severely reduces the constraint on the time step, allowing us to use large time steps, avoiding resolving the ultra-high gyro-frequency. We performed simulations in ultra-strong spatially and time-dependent electromagnetic fields, showing that our particle pusher is able to follow accurately the exact analytical solution for very long times. This property is crucial to properly capture for instance lepton electrodynamics in electromagnetic waves produced by fast rotating neutron stars. We conclude with a simple implementation of our new pusher into a one-dimensional relativistic electromagnetic particle-in-cell code, testing it against plasma oscillations, two-stream instabilities and strongly magnetized relativistic shocks.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2020. Published by Cambridge University Press
References
REFERENCES
- 11
- Cited by

