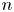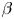1. Introduction
Magnetic confinement is currently considered the most promising way (Baalrud et al. Reference Baalrud, Ferraro, Garrison, Howard, Kuranz, Sarff, Scime and Solomon2020) to achieve the United States’ goal of building a pilot fusion power plant that generates net electricity before 2040 (National Academies of Sciences et al. 2021). Most advanced fusion reactor designs today are based on two main designs that use magnetic confinement: tokamaks and stellarators. These devices work by using strong magnetic fields to keep a hot, dense plasma at their centre. The main difference between tokamaks and stellarators lies in their geometric shape. Tokamaks are symmetric about a fixed axis, whereas stellarators are not. Due to the difference in axisymmetry, the tokamak equilibria are two-dimensional (2D) axisymmetric and the stellarator equilibria are three-dimensional (3D).
For a fixed magnetic field strength, the power density ![]() $P$ of a fusion device scales as
$P$ of a fusion device scales as ![]() $\beta ^2$, where
$\beta ^2$, where ![]() $\beta$ is the ratio of the plasma pressure to the magnetic pressure. Since current tokamaks and stellarators are low-
$\beta$ is the ratio of the plasma pressure to the magnetic pressure. Since current tokamaks and stellarators are low-![]() $\beta$ devices, one way to improve the efficiency of these devices is to increase the operating
$\beta$ devices, one way to improve the efficiency of these devices is to increase the operating ![]() $\beta$. However, doing so creates a large pressure gradient from the centre to the edge of the device, which is a source of a variety of pressure-driven, magnetohydrodynamic (MHD) and kinetic instabilities. An important category of pressure-driven instabilities are the high-
$\beta$. However, doing so creates a large pressure gradient from the centre to the edge of the device, which is a source of a variety of pressure-driven, magnetohydrodynamic (MHD) and kinetic instabilities. An important category of pressure-driven instabilities are the high-![]() $n$ ballooning modes.
$n$ ballooning modes.
In tokamaks, there have been numerous studies that have used the ideal ballooning mode to determine the plasma beta limit. This led to the development of codes such as EPED (Snyder et al. Reference Snyder, Burrell, Wilson, Chu, Fenstermacher, Leonard, Moyer, Osborne, Umansky and West2007) that can determine edge pressure profile with reasonable accuracy. In stellarators, the ideal ballooning mode might not cause a significant loss of energy, but Tang, Connor & Hastie (Reference Tang, Connor and Hastie1980) and Aleynikova et al. (Reference Aleynikova, Zocco, Xanthopoulos, Helander and Nührenberg2018) have shown that it is related to a kinetic instability known as the kinetic ballooning mode (KBM). Recent articles have shown the detrimental effects of KBM turbulence on stellarators for finite beta values (Aleynikova et al. Reference Aleynikova, Zocco, Xanthopoulos, Helander and Nührenberg2018; McKinney et al. Reference McKinney, Pueschel, Faber, Hegna, Ishizawa and Terry2021). The KBM is similar to the ideal ballooning mode, albeit with additional kinetic effects. Therefore, the ideal ballooning mode could be used as a proxy for KBM stability.
Numerous studies have been conducted to optimise tokamaks (Miller & Moore Reference Miller and Moore1979; Bernard & Moore Reference Bernard and Moore1981) and stellarators (Sanchez et al. Reference Sanchez, Hirshman, Ware, Berry and Spong2000a; Gates et al. Reference Gates, Boozer, Brown, Breslau, Curreli, Landreman, Lazerson, Lore, Mynick and Neilson2017) against ideal MHD instabilities. However, such calculations can be computationally costly and time consuming. In this paper, we use the self-adjoint property of ideal MHD to devise an adjoint-based method that speeds up the optimisation of 2D and 3D equilibria against the infinite-![]() $n$, ideal ballooning mode. Adjoint-based methods have been extensively used for aeronautical design (Giles & Pierce Reference Giles and Pierce2000) and recently in the context of stellarator optimisation (see Paul, Landreman & Antonsen (Reference Paul, Landreman and Antonsen2021) and references therein). Using this technique, we can speed up the process of finding equilibria that are stable against the ballooning mode.
$n$, ideal ballooning mode. Adjoint-based methods have been extensively used for aeronautical design (Giles & Pierce Reference Giles and Pierce2000) and recently in the context of stellarator optimisation (see Paul, Landreman & Antonsen (Reference Paul, Landreman and Antonsen2021) and references therein). Using this technique, we can speed up the process of finding equilibria that are stable against the ballooning mode.
The remainder of this paper is divided as follows: in § 2, we briefly describe the fundamentals of a general 3D MHD equilibrium and follow it with the details of the VMEC equilibrium solver (Hirshman & Whitson Reference Hirshman and Whitson1983) in § 2.1. Using VMEC, we obtain and present the details of one 2D axisymmetric equilibrium in § 2.2 and two 3D equilibria in§§ 2.3 and 2.4. In § 3, we present the physical, mathematical and numerical details used to solve the infinite-![]() $n$, ideal ballooning equation. We then analyse the susceptibility of the chosen local equilibria to the ideal ballooning instability. In § 3.3, we explain the self-adjoint property of the ideal ballooning equation. We briefly explain how the ballooning eigenvalue can be used as a proxy to stabilise the equilibria against the KBM. Using the self-adjoint technique, we formulate an adjoint method which we elucidate and test in § 4. In § 5, we present the details of the overall optimisation process and present an adjoint-based optimiser using the SIMSOPT (Landreman et al. Reference Landreman, Medasani, Wechsung, Giuliani, Jorge and Zhu2021) framework. In the penultimate section, we present our results, comparing the optimised stable equilibria with their initial, unstable counterparts. Finally, in § 7 we summarise our work and discuss possible ways in which it can be extended.
$n$, ideal ballooning equation. We then analyse the susceptibility of the chosen local equilibria to the ideal ballooning instability. In § 3.3, we explain the self-adjoint property of the ideal ballooning equation. We briefly explain how the ballooning eigenvalue can be used as a proxy to stabilise the equilibria against the KBM. Using the self-adjoint technique, we formulate an adjoint method which we elucidate and test in § 4. In § 5, we present the details of the overall optimisation process and present an adjoint-based optimiser using the SIMSOPT (Landreman et al. Reference Landreman, Medasani, Wechsung, Giuliani, Jorge and Zhu2021) framework. In the penultimate section, we present our results, comparing the optimised stable equilibria with their initial, unstable counterparts. Finally, in § 7 we summarise our work and discuss possible ways in which it can be extended.
2. Ideal MHD equilibrium
In this section, we start with the general form of a 3D, divergence-free magnetic field. We use this form to represent the magnetic field in tokamaks and stellarators. After that, we briefly describe the steady-state, ideal MHD, force-balance equation. In § 2.1, we explain the details of solving the ideal MHD force-balance equation using the VMEC code. Finally, we present the details of three MHD equilibria in §§ 2.2–2.4 that we will use throughout this study.
A divergence-free magnetic field ![]() $\boldsymbol {B}$ can be written in the Clebsch form (D'haeseleer et al. Reference D'haeseleer, Hitchon, Callen and Shohet2012)
$\boldsymbol {B}$ can be written in the Clebsch form (D'haeseleer et al. Reference D'haeseleer, Hitchon, Callen and Shohet2012)
The form (2.1) is generally used for tokamak equilibria. For stellarators, we use the following equivalent representation
We focus on solutions whose magnetic field lines lie on closed nested toroidal surfaces, known as flux surfaces. For tokamaks, we label the flux surfaces with their enclosed poloidal flux ![]() $\psi _{p}$ whereas for stellarators, we use the enclosed toroidal flux
$\psi _{p}$ whereas for stellarators, we use the enclosed toroidal flux ![]() $\psi$. On each flux surface, lines of constant
$\psi$. On each flux surface, lines of constant ![]() $\alpha _{t}$ and
$\alpha _{t}$ and ![]() $\alpha _{s}$ coincide with the magnetic field lines in tokamaks and stellarators, respectively. Thus, the variables
$\alpha _{s}$ coincide with the magnetic field lines in tokamaks and stellarators, respectively. Thus, the variables ![]() $\alpha _{t}$ and
$\alpha _{t}$ and ![]() $\alpha _{s}$ are known as field line labels.
$\alpha _{s}$ are known as field line labels.
To facilitate the calculation of various physical quantities from a general equilibrium solver, we use multiple coordinate systems. We use the right-handed cylindrical coordinate system ![]() $(R, \zeta, Z)$ where
$(R, \zeta, Z)$ where ![]() $R$ and
$R$ and ![]() $Z$ are the radial and vertical distances from the origin and
$Z$ are the radial and vertical distances from the origin and ![]() $\zeta$ is the azimuthal angle around the symmetry axis. We also define a curvilinear coordinate system comprising the
$\zeta$ is the azimuthal angle around the symmetry axis. We also define a curvilinear coordinate system comprising the ![]() $\mathrm {PEST}$ coordinates
$\mathrm {PEST}$ coordinates ![]() $(\psi _{p}, \zeta, \theta )$ where
$(\psi _{p}, \zeta, \theta )$ where ![]() $\psi _{p}$ is the flux surface label,
$\psi _{p}$ is the flux surface label, ![]() $\zeta$ is the cylindrical azimuthal angle and
$\zeta$ is the cylindrical azimuthal angle and ![]() $\theta$ is the ‘straight-field-line’ poloidal angle (D'haeseleer et al. Reference D'haeseleer, Hitchon, Callen and Shohet2012) such that
$\theta$ is the ‘straight-field-line’ poloidal angle (D'haeseleer et al. Reference D'haeseleer, Hitchon, Callen and Shohet2012) such that ![]() $\alpha _{t} = \zeta - q(\psi _{p})( \theta - \theta _0)$. Similarly, for 3D equilibria, we use the coordinate system
$\alpha _{t} = \zeta - q(\psi _{p})( \theta - \theta _0)$. Similarly, for 3D equilibria, we use the coordinate system ![]() $(\psi, \zeta, \theta )$ and
$(\psi, \zeta, \theta )$ and ![]() $\alpha _{s} = \theta - \iota (\psi )(\zeta - \zeta _0)$. The pitch of the magnetic field line on a flux surface is described by the safety factor
$\alpha _{s} = \theta - \iota (\psi )(\zeta - \zeta _0)$. The pitch of the magnetic field line on a flux surface is described by the safety factor
where ![]() $\iota$, the rotational transform, is the inverse of the safety factor. Using (2.1) or (2.2) for the magnetic field, one has to solve the steady-state ideal MHD force balance equation in the absence of a background flow
$\iota$, the rotational transform, is the inverse of the safety factor. Using (2.1) or (2.2) for the magnetic field, one has to solve the steady-state ideal MHD force balance equation in the absence of a background flow
where ![]() $p$ is the plasma pressure, and
$p$ is the plasma pressure, and ![]() $\boldsymbol {j}$ is the plasma current given by the Ampere's law
$\boldsymbol {j}$ is the plasma current given by the Ampere's law
where ![]() $\mu _0$ is the coefficient of permeability in vacuum. For axisymmetric equilibria, simplifying (2.4) yields the Grad–Shafranov equation (Shafranov Reference Shafranov1957; Grad & Rubin Reference Grad and Rubin1958). For a general 3D equilibrium, such an equation does not exist. However, we can solve for the axisymmetric and 3D cases using a general numerical equilibrium solver. In the following section, we explain how we use the numerical solver VMECFootnote 1 to obtain both 2D axisymmetric and 3D equilibria.
$\mu _0$ is the coefficient of permeability in vacuum. For axisymmetric equilibria, simplifying (2.4) yields the Grad–Shafranov equation (Shafranov Reference Shafranov1957; Grad & Rubin Reference Grad and Rubin1958). For a general 3D equilibrium, such an equation does not exist. However, we can solve for the axisymmetric and 3D cases using a general numerical equilibrium solver. In the following section, we explain how we use the numerical solver VMECFootnote 1 to obtain both 2D axisymmetric and 3D equilibria.
2.1. Numerical equilibrium solver
We generate numerical equilibria using the 3D equilibrium code VMEC (Hirshman & Whitson Reference Hirshman and Whitson1983). The code works by minimising the integral
subject to multiple geometric constraints (Kruskal & Kulsrud Reference Kruskal and Kulsrud1958). For our study, we used the fixed-boundary mode of VMEC. The fixed-boundary mode takes the shape of the boundary surface denoted by the cylindrical coordinates ![]() $R_{b}$ and
$R_{b}$ and ![]() $Z_{b}$ in terms of the Fourier-decomposed poloidal (
$Z_{b}$ in terms of the Fourier-decomposed poloidal (![]() $\varTheta$) and toroidal (
$\varTheta$) and toroidal (![]() $\zeta$) modes
$\zeta$) modes
 \begin{equation} \left. \begin{gathered} R_{b} = \sum_{n}\sum_{m} \hat{R}_{b}(m, n) \exp({\rm i}(m \varTheta - n \zeta)), \\ Z_{b} = \sum_{n}\sum_{m} \hat{Z}_{b}(m, n) \exp({\rm i}(m \varTheta - n \zeta)), \end{gathered} \right\} \end{equation}
\begin{equation} \left. \begin{gathered} R_{b} = \sum_{n}\sum_{m} \hat{R}_{b}(m, n) \exp({\rm i}(m \varTheta - n \zeta)), \\ Z_{b} = \sum_{n}\sum_{m} \hat{Z}_{b}(m, n) \exp({\rm i}(m \varTheta - n \zeta)), \end{gathered} \right\} \end{equation}
where ![]() $m$ and
$m$ and ![]() $n$ are integers. We also provide VMEC with the coefficients of the polynomials representing the global radial pressure
$n$ are integers. We also provide VMEC with the coefficients of the polynomials representing the global radial pressure ![]() $p(s)$ and the rotational transform
$p(s)$ and the rotational transform ![]() $\iota (s)$ as a function of the normalised toroidal flux
$\iota (s)$ as a function of the normalised toroidal flux ![]() $s$, and the total toroidal or poloidal flux enclosed by the boundary. The poloidal angle
$s$, and the total toroidal or poloidal flux enclosed by the boundary. The poloidal angle ![]() $\varTheta$ used by VMEC is related to the straight field line
$\varTheta$ used by VMEC is related to the straight field line ![]() $\theta$ by the following equation
$\theta$ by the following equation
where
For a boundary shape, pressure, rotational transform and enclosed toroidal flux, it solves for the flux surfaces. To achieve this, it uses a steepest descent method to minimise the energy integral in (2.6) on each surface for fixed ![]() $p$,
$p$, ![]() $\iota$, and enclosed flux subject to various topological constraints imposed by the ideal MHD. In a more compact form, VMEC solves
$\iota$, and enclosed flux subject to various topological constraints imposed by the ideal MHD. In a more compact form, VMEC solves
After running the code, we obtain the shape of the flux surfaces, the magnetic field and a set of important physical quantities. The characteristic physical quantities that we use in this work are defined as follows.
(i) The total enclosed toroidal flux by the boundary
 $\psi _{b} = \int \,\textrm {d}V \boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla } \zeta$.
$\psi _{b} = \int \,\textrm {d}V \boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla } \zeta$.(ii) The normalising magnetic field
 $B_{N} = \psi _{b}/({\rm \pi} a_{N}^2)$ where
$B_{N} = \psi _{b}/({\rm \pi} a_{N}^2)$ where  $a_{N} = \sqrt {\mathcal {A}_{b}/{\rm \pi} }$ is the effective minor radius and
$a_{N} = \sqrt {\mathcal {A}_{b}/{\rm \pi} }$ is the effective minor radius and  $\mathcal {A}_{b}$ is the average area enclosed by the boundary (averaged over
$\mathcal {A}_{b}$ is the average area enclosed by the boundary (averaged over  $\zeta$).
$\zeta$).(iii) The ratio of the total plasma pressure to the magnetic pressure on the magnetic axis
 $\beta _{\mathrm {ax}} = 2 \mu _0 p(s=0)/B_{N}^2$.
$\beta _{\mathrm {ax}} = 2 \mu _0 p(s=0)/B_{N}^2$.(iv) The aspect ratio
 $A$ and the normalised minor radius
$A$ and the normalised minor radius  $a_{N}$ of the device.
$a_{N}$ of the device.(v) The radius of curvature of the boundary
 $R_c(\theta ) = ({\textrm {d}^2\!R}/{\textrm {d}Z^2})/(1 + ({\textrm {d}R}/{\textrm {d}Z})^2)^{3/2}$ where
$R_c(\theta ) = ({\textrm {d}^2\!R}/{\textrm {d}Z^2})/(1 + ({\textrm {d}R}/{\textrm {d}Z})^2)^{3/2}$ where  $R$ and
$R$ and  $Z$ are the cylindrical coordinates used to parametrise the boundary.
$Z$ are the cylindrical coordinates used to parametrise the boundary.(vi) The volume-averaged, normalised plasma pressure
 $\langle \beta \rangle = \int \,\textrm {d}V p/\int \,\textrm {d}V B^2$ where
$\langle \beta \rangle = \int \,\textrm {d}V p/\int \,\textrm {d}V B^2$ where  $\textrm {d}V$ is the differential volume element.
$\textrm {d}V$ is the differential volume element.(vii) The total enclosed toroidal current
 $j_{\zeta }$ =
$j_{\zeta }$ =  $\lvert \int \,\textrm {d}V\, (\boldsymbol {j}\boldsymbol {\cdot } \boldsymbol {\nabla } \zeta )\rvert$.
$\lvert \int \,\textrm {d}V\, (\boldsymbol {j}\boldsymbol {\cdot } \boldsymbol {\nabla } \zeta )\rvert$.(viii) The volume-averaged magnetic field
 $\langle B \rangle = \int \,\textrm {d}V B/\sqrt {V}$ where
$\langle B \rangle = \int \,\textrm {d}V B/\sqrt {V}$ where  $\textrm {d}V$ is the differential volume element.
$\textrm {d}V$ is the differential volume element.(ix) The mean rotational transform
 $\bar {\iota } = \int \,\textrm {d}s \, \iota /\int \,\textrm {d}s$.
$\bar {\iota } = \int \,\textrm {d}s \, \iota /\int \,\textrm {d}s$.
Using VMEC, we generate three equilibria: an axisymmetric equilibrium with a DIII-D-like boundary shape and two 3D equilibria, modified NCSX- and modified Henneberg-QA. In the following sections, we provide important details for each of these equilibria.
2.2. 2D axisymmetric equilibrium
In this study, the first equilibrium that we choose is a high-![]() $\beta$, axisymmetric, DIII-D-like equilibrium with a negative triangularity boundary: a boundary that looks like an inverted-D. Negative triangularity equilibria have generally been found to have enhanced confinement Marinoni et al. (Reference Marinoni, Austin, Hyatt, Walker, Candy, Chrystal, Lasnier, McKee, Odstrčil and Petty2019) and stability against edge localised modes. We then choose a negative triangularity equilibrium from Gaur et al. (Reference Gaur, Abel, Dickinson and Dorland2023) where it is shown to be unstable against the ideal ballooning mode. With this equilibrium as an initial state, we run our ideal ballooning stability optimisation to find a stable equilibrium while maintaining a boundary shape with negative triangularity. The input pressure, the rotational transform and the boundary shape profile for this equilibrium are shown in figure 1.
$\beta$, axisymmetric, DIII-D-like equilibrium with a negative triangularity boundary: a boundary that looks like an inverted-D. Negative triangularity equilibria have generally been found to have enhanced confinement Marinoni et al. (Reference Marinoni, Austin, Hyatt, Walker, Candy, Chrystal, Lasnier, McKee, Odstrčil and Petty2019) and stability against edge localised modes. We then choose a negative triangularity equilibrium from Gaur et al. (Reference Gaur, Abel, Dickinson and Dorland2023) where it is shown to be unstable against the ideal ballooning mode. With this equilibrium as an initial state, we run our ideal ballooning stability optimisation to find a stable equilibrium while maintaining a boundary shape with negative triangularity. The input pressure, the rotational transform and the boundary shape profile for this equilibrium are shown in figure 1.

Figure 1. Plots of the inputs to the VMEC code for the DIII-D-like design: (a) the pressure, (b) the rotational transform as a function of the normalised toroidal flux ![]() $s$ and (c) the cross section of the boundary.
$s$ and (c) the cross section of the boundary.
Using these inputs, we run VMEC to obtain the global MHD equilibrium. Our optimiser sometimes finds solutions that meet the ideal ballooning stability constraints in a trivial fashion. For example, the optimiser may give us a large aspect ratio or decrease the minor radius causing the volume averaged ![]() $B$ to increase, causing the
$B$ to increase, causing the ![]() $\beta$ to decrease. To avoid these trivial solutions, we have to impose additional constraints on important characteristic physical quantities to prevent them from changing significantly. The values of the relevant physical quantities for this equilibrium are provided in table 1.
$\beta$ to decrease. To avoid these trivial solutions, we have to impose additional constraints on important characteristic physical quantities to prevent them from changing significantly. The values of the relevant physical quantities for this equilibrium are provided in table 1.
Table 1. Relevant physical quantities for the DIII-D-like equilibrium.
2.3. Modified NCSX equilibrium
The second equilibrium we select is the 3D equilibrium for the NCSX design (Zarnstorff et al. Reference Zarnstorff, Berry, Brooks, Fredrickson, Fu, Hirshman, Hudson, Ku, Lazarus and Mikkelsen2001; Fu et al. Reference Fu, Isaev, Ku, Mikhailov, Redi, Sanchez, Subbotin, Cooper, Hirshman and Monticello2007). This equilibrium is designed to have a hidden symmetry known as quasisymmetry (Boozer Reference Boozer1983; Garren & Boozer Reference Garren and Boozer1991) where the strength of the magnetic field ![]() $|\boldsymbol {B}|$ does not change along a special coordinate. QuasisymmetryFootnote 2 is a useful property because it ensures orbit confinement, which helps improve energetic particle confinement, a major issue in stellarators. The pressure, rotational transform and boundary shape profile for this equilibrium are shown in figure 2.
$|\boldsymbol {B}|$ does not change along a special coordinate. QuasisymmetryFootnote 2 is a useful property because it ensures orbit confinement, which helps improve energetic particle confinement, a major issue in stellarators. The pressure, rotational transform and boundary shape profile for this equilibrium are shown in figure 2.

Figure 2. Plots of the inputs to the VMEC code for the modified NCSX design: (a) the pressure, (b) the rotational transform as a function of the normalised toroidal flux ![]() $s$ and (c) the cross section of the boundary. Note the large negative shear until
$s$ and (c) the cross section of the boundary. Note the large negative shear until ![]() $s \approx 0.85$.
$s \approx 0.85$.
The values of equilibrium-dependent quantities output by VMEC are presented in table 2.
Table 2. Important physical quantities for the modified NCSX equilibrium.
2.4. Modified Henneberg-QA
The final equilibrium we study is the modified Henneberg-QA design (Henneberg et al. Reference Henneberg, Drevlak, Nührenberg, Beidler, Turkin, Loizu and Helander2019). This equilibrium is also designed to have quasisymmetry for a wide variety of pressure profiles. The pressure, rotational transform and boundary shape profile for this equilibrium are shown in figure 3.

Figure 3. Plots of the inputs to the VMEC code for the modified Henneberg-QA design: (a) the pressure, (b) the rotational transform as a function of the normalised toroidal flux ![]() $s$ and (c) the cross section of the boundary.
$s$ and (c) the cross section of the boundary.
For reasons explained in the previous section, we impose additional constraints on some of the physical quantities. The values of these equilibrium-dependent parameters that we use as constraints in § 6 are presented in table 3.
Table 3. Relevant physical quantities for the modified Henneberg-QA design.
In the following section, we describe the ideal ballooning stability and analyse these equilibria by measuring their instability against the ideal ballooning mode.
3. The infinite- $n$ ideal ballooning mode
$n$ ideal ballooning mode
In this section, we present the details of the infinite-![]() $n$ ideal ballooning mode. In § 3.1, we briefly describe its theoretical foundation and mathematical formulation. In § 3.2, we present a numerical technique used to solve the ideal ballooning equation. In § 3.3, we describe the mathematical properties that we use to formulate an adjoint-based method and accelerate optimisation against the ideal ballooning mode. In the final section, we describe how optimisation against the ideal ballooning mode can speed up optimisation against an electromagnetic mode seen in kinetic plasma turbulence, known as the KBM.
$n$ ideal ballooning mode. In § 3.1, we briefly describe its theoretical foundation and mathematical formulation. In § 3.2, we present a numerical technique used to solve the ideal ballooning equation. In § 3.3, we describe the mathematical properties that we use to formulate an adjoint-based method and accelerate optimisation against the ideal ballooning mode. In the final section, we describe how optimisation against the ideal ballooning mode can speed up optimisation against an electromagnetic mode seen in kinetic plasma turbulence, known as the KBM.
3.1. Physical and mathematical description
This work involves a detailed analysis of three equilibria against an important MHD instability, the infinite-![]() $n$ ideal ballooning instability (Connor, Hastie & Taylor Reference Connor, Hastie and Taylor1979; Dewar & Glasser Reference Dewar and Glasser1983): a field-aligned, pressure-driven Alfvén wave that grows when the destabilising pressure gradient in the region of ‘bad’ curvature exceeds the stabilising effect of field-line bending. Using magnetic field unit vector
$n$ ideal ballooning instability (Connor, Hastie & Taylor Reference Connor, Hastie and Taylor1979; Dewar & Glasser Reference Dewar and Glasser1983): a field-aligned, pressure-driven Alfvén wave that grows when the destabilising pressure gradient in the region of ‘bad’ curvature exceeds the stabilising effect of field-line bending. Using magnetic field unit vector ![]() $\boldsymbol {b} = \boldsymbol {B}/B$, the region of ‘bad’ curvature is defined as a region of a flux surface where
$\boldsymbol {b} = \boldsymbol {B}/B$, the region of ‘bad’ curvature is defined as a region of a flux surface where ![]() $(\boldsymbol {b}\boldsymbol {\cdot }\boldsymbol {\nabla } \boldsymbol {b}) \boldsymbol {\cdot } \boldsymbol {\nabla } p > 0$.
$(\boldsymbol {b}\boldsymbol {\cdot }\boldsymbol {\nabla } \boldsymbol {b}) \boldsymbol {\cdot } \boldsymbol {\nabla } p > 0$.
The ideal ballooning equation
 \begin{align}
\frac{1}{\mathcal{J}}\frac{\partial}{\partial \theta}\left(
\frac{\lvert \boldsymbol{\nabla}\alpha_{t} \rvert^2
}{\mathcal{J}\, B^2} \frac{\partial \hat{X}}{\partial
\theta}\right) + 2 \frac{1}{B^4} \frac{{\rm d}(\mu_0 p)}{{\rm
d}\psi}\left[
\boldsymbol{B}\times\boldsymbol{\nabla}\left(\mu_0 p +
\frac{B^2}{2}\right)\boldsymbol{\cdot}\boldsymbol{\nabla}{\alpha_{t}}\right]
\hat{X} ={-}\rho \omega^2
\frac{\lvert\boldsymbol{\nabla}\alpha_{t}\rvert^2}{B^2}
\hat{X},
\end{align}
\begin{align}
\frac{1}{\mathcal{J}}\frac{\partial}{\partial \theta}\left(
\frac{\lvert \boldsymbol{\nabla}\alpha_{t} \rvert^2
}{\mathcal{J}\, B^2} \frac{\partial \hat{X}}{\partial
\theta}\right) + 2 \frac{1}{B^4} \frac{{\rm d}(\mu_0 p)}{{\rm
d}\psi}\left[
\boldsymbol{B}\times\boldsymbol{\nabla}\left(\mu_0 p +
\frac{B^2}{2}\right)\boldsymbol{\cdot}\boldsymbol{\nabla}{\alpha_{t}}\right]
\hat{X} ={-}\rho \omega^2
\frac{\lvert\boldsymbol{\nabla}\alpha_{t}\rvert^2}{B^2}
\hat{X},
\end{align}
is a second-order eigenvalue differential equation that calculates the perturbation ![]() $\hat {X}(\theta )$ along the ballooning coordinate
$\hat {X}(\theta )$ along the ballooning coordinate ![]() $\theta$ and its eigenvalue (or the square of the growth rate)
$\theta$ and its eigenvalue (or the square of the growth rate) ![]() $-\omega ^2$. In (3.1),
$-\omega ^2$. In (3.1), ![]() $\rho$ is the plasma mass density,
$\rho$ is the plasma mass density, ![]() $\mathcal {J} = (\boldsymbol {B}\boldsymbol {\cdot } \boldsymbol {\nabla } \theta )^{-1}$ and the rest of the terms are defined in § 2. This equation is solved subject to the following condition on the eigenfunction
$\mathcal {J} = (\boldsymbol {B}\boldsymbol {\cdot } \boldsymbol {\nabla } \theta )^{-1}$ and the rest of the terms are defined in § 2. This equation is solved subject to the following condition on the eigenfunction
where ![]() $\theta _0$ is the ballooning parameter.Footnote 3 Details of the derivation of the ideal ballooning equation are given in Connor et al. (Reference Connor, Hastie and Taylor1979) and Dewar & Glasser (Reference Dewar and Glasser1983).
$\theta _0$ is the ballooning parameter.Footnote 3 Details of the derivation of the ideal ballooning equation are given in Connor et al. (Reference Connor, Hastie and Taylor1979) and Dewar & Glasser (Reference Dewar and Glasser1983).
The ballooning equation balances the stabilising field-line bending term and the destabilising pressure gradient with the inertia of the resulting Alfvén wave, oscillating with a frequency ![]() $\omega$. Note that (3.1) depends on
$\omega$. Note that (3.1) depends on ![]() $\psi$ (or
$\psi$ (or ![]() $\psi _{p}$) as a parameter, and we can compute the coefficients from the equilibrium quantities on each surface. Before solving (3.1) numerically, we normalise and write the ballooning equation on a field line (fixed
$\psi _{p}$) as a parameter, and we can compute the coefficients from the equilibrium quantities on each surface. Before solving (3.1) numerically, we normalise and write the ballooning equation on a field line (fixed ![]() $\alpha _{t}$) as
$\alpha _{t}$) as
where
 \begin{equation} \left. \begin{gathered}
{g} =
(\boldsymbol{b}\boldsymbol{\cdot}\boldsymbol{\nabla}_{N}
\theta) \frac{\lvert \boldsymbol{\nabla}_{N}\alpha_{t}
\rvert^2}{B/B_{N}},\\ {c} =
\frac{2}{(\boldsymbol{b}\boldsymbol{\cdot}\boldsymbol{\nabla}_{N}
\theta)}\, \frac{1}{(B/B_{N})^{4}}\, \frac{{\rm d} (\mu_0 p/B_{N}^2)}{{\rm
d}\psi_{N}}\left[\boldsymbol{b} \times
\boldsymbol{\nabla}_{N} \left(\frac{2\mu_0 p + B^2}{2
B_{N}^2}\right) \boldsymbol{\cdot} \boldsymbol{\nabla}_{N}
\alpha_{t} \right],\\ {f} = \frac{1}{(\boldsymbol{b}\boldsymbol{\cdot}\boldsymbol{\nabla}_{N}
\theta)}\, \frac{\lvert
\boldsymbol{\nabla}_{N} \alpha_{t} \rvert
^2}{(B/B_{N})^3},\\ \hat{\lambda} ={-}\left(\frac{\omega
a_{N}}{v_{A}}\right)^2,\quad v_{A} =
\frac{B_{N}}{\sqrt{4{\rm \pi} \rho}}, \end{gathered}
\right\}
\end{equation}
\begin{equation} \left. \begin{gathered}
{g} =
(\boldsymbol{b}\boldsymbol{\cdot}\boldsymbol{\nabla}_{N}
\theta) \frac{\lvert \boldsymbol{\nabla}_{N}\alpha_{t}
\rvert^2}{B/B_{N}},\\ {c} =
\frac{2}{(\boldsymbol{b}\boldsymbol{\cdot}\boldsymbol{\nabla}_{N}
\theta)}\, \frac{1}{(B/B_{N})^{4}}\, \frac{{\rm d} (\mu_0 p/B_{N}^2)}{{\rm
d}\psi_{N}}\left[\boldsymbol{b} \times
\boldsymbol{\nabla}_{N} \left(\frac{2\mu_0 p + B^2}{2
B_{N}^2}\right) \boldsymbol{\cdot} \boldsymbol{\nabla}_{N}
\alpha_{t} \right],\\ {f} = \frac{1}{(\boldsymbol{b}\boldsymbol{\cdot}\boldsymbol{\nabla}_{N}
\theta)}\, \frac{\lvert
\boldsymbol{\nabla}_{N} \alpha_{t} \rvert
^2}{(B/B_{N})^3},\\ \hat{\lambda} ={-}\left(\frac{\omega
a_{N}}{v_{A}}\right)^2,\quad v_{A} =
\frac{B_{N}}{\sqrt{4{\rm \pi} \rho}}, \end{gathered}
\right\}
\end{equation}
where ![]() $v_{A}$ is the Alfvén speed and the values and definitions of the effective minor radius
$v_{A}$ is the Alfvén speed and the values and definitions of the effective minor radius ![]() $a_{N}$ and the normalising magnetic field
$a_{N}$ and the normalising magnetic field ![]() $B_{N}$ are the normalising length and magnetic field strength, respectively, defined in § 2.1. The normalised gradient
$B_{N}$ are the normalising length and magnetic field strength, respectively, defined in § 2.1. The normalised gradient ![]() $\boldsymbol {\nabla }_{N} = a_{N}\boldsymbol {\nabla }$. In the next section, we present the numerical procedure used to solve the ideal ballooning equation.
$\boldsymbol {\nabla }_{N} = a_{N}\boldsymbol {\nabla }$. In the next section, we present the numerical procedure used to solve the ideal ballooning equation.
3.2. Numerical implementation and eigenvalues of the selected equilibria
In this section, we briefly discuss the numerical technique used to solve the ballooning equation (3.3). Our numerical technique is virtually identical to that used by Sanchez et al. (Reference Sanchez, Hirshman, Whitson and Ware2000b) in their ballooning solver COBRAVMEC. After briefly explaining the details of our solver, we present the maximum eigenvalue as a function of the normalised toroidal flux ![]() $s$ for the three equilibria we presented in § 2.
$s$ for the three equilibria we presented in § 2.
The ideal ballooning equation is a second-order ordinary differential equation with real-valued coefficients. This eigenvalue equation is discretised using a second-order accurate, central-finite-difference scheme
subject to the boundary conditions
where ![]() $N$ is an odd number of uniformly spaced points in the ballooning space,
$N$ is an odd number of uniformly spaced points in the ballooning space, ![]() $\theta _{b}$ is a finite user-selected value that determines the extent of the eigenfunction such that
$\theta _{b}$ is a finite user-selected value that determines the extent of the eigenfunction such that ![]() $\theta _j \in [-\theta _{b}, \theta _{b}]$ and
$\theta _j \in [-\theta _{b}, \theta _{b}]$ and ![]() $\Delta \theta = \theta _{j+1} - \theta _{j}$. First-order derivatives are evaluated at half points
$\Delta \theta = \theta _{j+1} - \theta _{j}$. First-order derivatives are evaluated at half points ![]() $j-1/2, j-3/2$ instead of grid points to ensure numerical stability. For a fixed poloidal and toroidal resolution, the time taken by our solver is proportional to
$j-1/2, j-3/2$ instead of grid points to ensure numerical stability. For a fixed poloidal and toroidal resolution, the time taken by our solver is proportional to ![]() $\theta _{b}$. Therefore, it is important to find the right balance between speed and accuracy. Throughout this work, we chose the domain limit
$\theta _{b}$. Therefore, it is important to find the right balance between speed and accuracy. Throughout this work, we chose the domain limit ![]() $\theta _{b} = 5{\rm \pi}$ for all calculations, as we found it to be a sufficient range to capture the ballooning eigenfunction. We observed that the values
$\theta _{b} = 5{\rm \pi}$ for all calculations, as we found it to be a sufficient range to capture the ballooning eigenfunction. We observed that the values ![]() $\theta _{b} > 5{\rm \pi}$ made a relatively small difference from the value obtained of
$\theta _{b} > 5{\rm \pi}$ made a relatively small difference from the value obtained of ![]() $\hat {\lambda }$. The discrete set of (3.5) is written in the form of a matrix equation
$\hat {\lambda }$. The discrete set of (3.5) is written in the form of a matrix equation
where the exact matrix ![]() $\boldsymbol{\mathsf{A}}$ is provided in Appendix A. We then solve (3.7) to find the largest eigenvalue using an Arnoldi iterative scheme using the scipy.linalg.eigs solver in Python and refine the accuracy of the largest eigenvalue in the grid spacing
$\boldsymbol{\mathsf{A}}$ is provided in Appendix A. We then solve (3.7) to find the largest eigenvalue using an Arnoldi iterative scheme using the scipy.linalg.eigs solver in Python and refine the accuracy of the largest eigenvalue in the grid spacing ![]() $\Delta \theta$ using variational refinement
$\Delta \theta$ using variational refinement
 \begin{equation} \hat{\lambda} = \frac{\int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta \left({c} \lvert \hat{X}\rvert^2 - {g} \left\lvert \dfrac{{\rm d}\!\hat{X}}{{\rm d}\theta}\right\rvert^2 \right)}{\int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta\, {f}\lvert \hat{X}\rvert^2}, \end{equation}
\begin{equation} \hat{\lambda} = \frac{\int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta \left({c} \lvert \hat{X}\rvert^2 - {g} \left\lvert \dfrac{{\rm d}\!\hat{X}}{{\rm d}\theta}\right\rvert^2 \right)}{\int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta\, {f}\lvert \hat{X}\rvert^2}, \end{equation}
where the derivative ![]() $\textrm {d}\hat {X}/\textrm {d}\theta$ is calculated using a fourth-order accurate finite-difference scheme and the integral is performed using a fourth-order accurate Simpson's rule (
$\textrm {d}\hat {X}/\textrm {d}\theta$ is calculated using a fourth-order accurate finite-difference scheme and the integral is performed using a fourth-order accurate Simpson's rule (![]() $1/3$ rule) with scipy.integrate.simps.Footnote 4 Note that we only solve for and refine the largest eigenvalue of (3.3) and not the entire eigenvalue spectrum.
$1/3$ rule) with scipy.integrate.simps.Footnote 4 Note that we only solve for and refine the largest eigenvalue of (3.3) and not the entire eigenvalue spectrum.
3.3. Properties of the ideal ballooning equation
The ideal ballooning (3.3) is a linear equation that can be written as
where the linear operator
and the coefficients ![]() ${g, c, f}$ are real-valued functions along a field line. Mathematically, the solutions of (3.9) form the basis for the Hilbert space equipped with the following inner product
${g, c, f}$ are real-valued functions along a field line. Mathematically, the solutions of (3.9) form the basis for the Hilbert space equipped with the following inner product
and are square integrable, i.e.![]() $\langle \hat {X}, \hat {X} \rangle < \infty$. Owing to the self-adjoint nature of ideal MHD (Freidberg Reference Freidberg2014), for solutions
$\langle \hat {X}, \hat {X} \rangle < \infty$. Owing to the self-adjoint nature of ideal MHD (Freidberg Reference Freidberg2014), for solutions ![]() $\hat {X}_1$ and
$\hat {X}_1$ and ![]() $\hat {X}_2$ of (3.9) the operator
$\hat {X}_2$ of (3.9) the operator ![]() $\mathcal {L}$ satisfies the following property:
$\mathcal {L}$ satisfies the following property:
where we have used the boundary condition ![]() $\lim _{\theta \rightarrow \pm \infty } \hat {X}_1 = \lim _{\theta \rightarrow \pm \infty } \hat {X}_2 = 0$. Using (3.12), one can show that all eigenvalues
$\lim _{\theta \rightarrow \pm \infty } \hat {X}_1 = \lim _{\theta \rightarrow \pm \infty } \hat {X}_2 = 0$. Using (3.12), one can show that all eigenvalues ![]() $\hat {\lambda }$ (3.1) will be real numbers. Therefore,
$\hat {\lambda }$ (3.1) will be real numbers. Therefore, ![]() $\omega = \pm \textrm {i}\sqrt {\hat {\lambda }}$ will be purely real, an oscillating mode, or purely imaginary, a growing mode. We refer to oscillating modes as stable and to growing modes as unstable. We use this powerful property in § 4 to formulate an adjoint method, a technique that can speed up the calculation of the gradient of
$\omega = \pm \textrm {i}\sqrt {\hat {\lambda }}$ will be purely real, an oscillating mode, or purely imaginary, a growing mode. We refer to oscillating modes as stable and to growing modes as unstable. We use this powerful property in § 4 to formulate an adjoint method, a technique that can speed up the calculation of the gradient of ![]() $\hat {\lambda }_{\mathrm {max}}$ on each flux surface.
$\hat {\lambda }_{\mathrm {max}}$ on each flux surface.
3.4. Relation to the KBM
In this section, we explain how the ideal ballooning equation is directly related to an important mode of gyrokinetic plasma turbulence known as the KBM. Unlike ideal MHD which is a fluid theory, a single fluid with properties that vary in configuration space, a gyrokinetic model takes into account the distribution of different ion and electron species in both configuration and velocity space. Using a gyrokinetic model, Tang et al. (Reference Tang, Connor and Hastie1980) and Aleynikova et al. (Reference Aleynikova, Zocco, Xanthopoulos, Helander and Nührenberg2018) have shown that for devices with a large aspect ratio, modes with wavenumbers ![]() $k_y \ll 1/\rho _{i}$, where
$k_y \ll 1/\rho _{i}$, where ![]() $\rho _i = e B/m_{i}$ is the ion gyroradius and
$\rho _i = e B/m_{i}$ is the ion gyroradius and ![]() $m_{i}$ is the ion mass, the gyrokinetic model can be reduced to the ideal ballooning equation with corrections that depend on
$m_{i}$ is the ion mass, the gyrokinetic model can be reduced to the ideal ballooning equation with corrections that depend on ![]() $k_y\rho _{i}$:
$k_y\rho _{i}$:
where
where ![]() $c_0$ is a constant on a flux surface and
$c_0$ is a constant on a flux surface and ![]() $k_y \rho _{i}$ is the normalised wavenumber of the mode in the long wavelength limit, i.e.
$k_y \rho _{i}$ is the normalised wavenumber of the mode in the long wavelength limit, i.e.![]() $k_y \rho _i \rightarrow 0$, we recover the ideal ballooning equation exactly. this means that an ideal ballooning unstable mode is also unstable to the KBM. In fact, the KBM is an ideal ballooning mode with kinetic effects.
$k_y \rho _i \rightarrow 0$, we recover the ideal ballooning equation exactly. this means that an ideal ballooning unstable mode is also unstable to the KBM. In fact, the KBM is an ideal ballooning mode with kinetic effects.
Using a simple mixing-length argument, one can qualitatively argue that the turbulence heat flux diffusion is
where ![]() $\mathrm {Im}(\omega )$ is the imaginary part of
$\mathrm {Im}(\omega )$ is the imaginary part of ![]() $\omega$ also called the growth rate. This implies that low-wavenumber turbulence has the highest rate of diffusion and leads to poor plasma confinement. Hence, even if ideal ballooning unstable modes do not lead to disruption in stellarators, they could lead to a large heat flux transport through the KBM channel. Since calculating KBM growth rates using a microstability code is expensive, one can use ideal ballooning stability as a necessary condition for KBM stability to optimise against the KBM.Footnote 5 For tokamaks, this is one of the fundamental ideas currently used in the EPED code (Snyder et al. Reference Snyder, Burrell, Wilson, Chu, Fenstermacher, Leonard, Moyer, Osborne, Umansky and West2007) to predict the plasma pressure profile in the pedestal region.
$\omega$ also called the growth rate. This implies that low-wavenumber turbulence has the highest rate of diffusion and leads to poor plasma confinement. Hence, even if ideal ballooning unstable modes do not lead to disruption in stellarators, they could lead to a large heat flux transport through the KBM channel. Since calculating KBM growth rates using a microstability code is expensive, one can use ideal ballooning stability as a necessary condition for KBM stability to optimise against the KBM.Footnote 5 For tokamaks, this is one of the fundamental ideas currently used in the EPED code (Snyder et al. Reference Snyder, Burrell, Wilson, Chu, Fenstermacher, Leonard, Moyer, Osborne, Umansky and West2007) to predict the plasma pressure profile in the pedestal region.
In summary, in this section, we have explained the mathematical, physical and numerical methods used to solve the ideal ballooning equation. We have also explained the self-adjoint property of the ideal ballooning equation and the crucial link between the ideal ballooning mode and KBM. In the next section, we use the self-adjoint property of the ideal ballooning equation to outline and test the adjoint method.
4. Developing an adjoint method
In this section, we derive and explain the process of calculating the gradients of the ideal ballooning eigenvalue ![]() $\hat {\lambda }$ using an adjoint method. Using this method, we find the maximum eigenvalue
$\hat {\lambda }$ using an adjoint method. Using this method, we find the maximum eigenvalue ![]() $\hat {\lambda }_\textrm {max}$ on each flux surface. We then elucidate how this technique is faster than the conventional gradient-based method and illustrate this by plotting gradients from a typical optimisation run and calculating the speed-up.
$\hat {\lambda }_\textrm {max}$ on each flux surface. We then elucidate how this technique is faster than the conventional gradient-based method and illustrate this by plotting gradients from a typical optimisation run and calculating the speed-up.
To find ![]() $\hat {\lambda }_\textrm {max}$ on each flux surface, we need the gradient of the eigenvalue of a general function
$\hat {\lambda }_\textrm {max}$ on each flux surface, we need the gradient of the eigenvalue of a general function ![]() $\mathcal {H}$ such that
$\mathcal {H}$ such that ![]() $\mathcal {H}$ is maximised if and only if
$\mathcal {H}$ is maximised if and only if ![]() $\hat {\lambda } = \hat {\lambda }_\textrm {max}$. Mathematically, this problem can be defined as follows
$\hat {\lambda } = \hat {\lambda }_\textrm {max}$. Mathematically, this problem can be defined as follows
where ![]() $\hat {\lambda }$ is the eigenvalue,
$\hat {\lambda }$ is the eigenvalue, ![]() $\hat {X}$ is the eigenfunction,
$\hat {X}$ is the eigenfunction, ![]() $\tilde {\boldsymbol {p}}$ is the state vector that contains all the equilibrium parameters such as the boundary shape and
$\tilde {\boldsymbol {p}}$ is the state vector that contains all the equilibrium parameters such as the boundary shape and ![]() $\hat {\boldsymbol {p}} = (\alpha _{t}, \theta _0)$ is a vector that contains the parameters of the ideal ballooning equation,
$\hat {\boldsymbol {p}} = (\alpha _{t}, \theta _0)$ is a vector that contains the parameters of the ideal ballooning equation, ![]() $\mathcal {H}$ is an objective function and
$\mathcal {H}$ is an objective function and ![]() $\mathcal {G}$ is the ideal ballooning operator. To maximise
$\mathcal {G}$ is the ideal ballooning operator. To maximise ![]() $\mathcal {H}$ on a flux surface for a given equilibrium, i.e.for a fixed
$\mathcal {H}$ on a flux surface for a given equilibrium, i.e.for a fixed ![]() $\tilde {\boldsymbol {p}}$, we need the gradient
$\tilde {\boldsymbol {p}}$, we need the gradient
 \begin{equation} \frac{{\rm d} \mathcal{H}}{{\rm d} \hat{\boldsymbol{p}}} = \left.\frac{\partial \mathcal{H}}{\partial \hat{\lambda}}\right\lvert_{\hat{\boldsymbol{p}}} \frac{\partial \hat{\lambda}}{\partial \hat{\boldsymbol{p}}} + \left.\frac{\partial \mathcal{H}}{\partial \hat{\boldsymbol{p}}}\right\lvert_{\hat{\lambda}}. \end{equation}
\begin{equation} \frac{{\rm d} \mathcal{H}}{{\rm d} \hat{\boldsymbol{p}}} = \left.\frac{\partial \mathcal{H}}{\partial \hat{\lambda}}\right\lvert_{\hat{\boldsymbol{p}}} \frac{\partial \hat{\lambda}}{\partial \hat{\boldsymbol{p}}} + \left.\frac{\partial \mathcal{H}}{\partial \hat{\boldsymbol{p}}}\right\lvert_{\hat{\lambda}}. \end{equation}
The most expensive term to calculate in (4.2) is the gradient of the eigenvalue ![]() $\lambda$.Footnote 6 To obtain that, we expand the equation
$\lambda$.Footnote 6 To obtain that, we expand the equation ![]() $\textrm {d} \mathcal {G}/\textrm {d} \hat {\boldsymbol {p}} = 0$ at a constant
$\textrm {d} \mathcal {G}/\textrm {d} \hat {\boldsymbol {p}} = 0$ at a constant ![]() $\tilde {\boldsymbol {p}}$
$\tilde {\boldsymbol {p}}$
 \begin{equation} -\frac{\partial \mathcal{G}}{\partial \hat{\lambda}}\frac{\partial \hat{\lambda}}{\partial \hat{\boldsymbol{p}}} = \frac{\partial \mathcal{G}}{\partial \hat{X}} \frac{\partial \hat{X}}{\partial \hat{\boldsymbol{p}}} + \left.\frac{\partial \mathcal{G}}{\partial \hat{\boldsymbol{p}}}\right\lvert_{\hat{X}, \hat{\lambda}}. \end{equation}
\begin{equation} -\frac{\partial \mathcal{G}}{\partial \hat{\lambda}}\frac{\partial \hat{\lambda}}{\partial \hat{\boldsymbol{p}}} = \frac{\partial \mathcal{G}}{\partial \hat{X}} \frac{\partial \hat{X}}{\partial \hat{\boldsymbol{p}}} + \left.\frac{\partial \mathcal{G}}{\partial \hat{\boldsymbol{p}}}\right\lvert_{\hat{X}, \hat{\lambda}}. \end{equation}This equation can be explicitly written with the help of (3.10)
To simplify (4.4) further, we multiply it by the eigenfunction ![]() $\hat {X}^{*}$ and integrate it throughout the domain
$\hat {X}^{*}$ and integrate it throughout the domain ![]() $\theta \in [-\theta _{b}, \theta _{b}]$. Upon doing that, we use the self-adjoint property (3.12) and work through the algebra (given in Appendix B) to obtain the adjoint relation
$\theta \in [-\theta _{b}, \theta _{b}]$. Upon doing that, we use the self-adjoint property (3.12) and work through the algebra (given in Appendix B) to obtain the adjoint relation
 \begin{equation} \frac{\partial \hat{\lambda}}{\partial \hat{\boldsymbol{p}}} = \frac{\int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta \left(\dfrac{\partial {c}}{\partial \hat{\boldsymbol{p}}} \lvert \hat{X}\rvert^2 - \dfrac{\partial {g}}{\partial \hat{\boldsymbol{p}}}\left\lvert \dfrac{{\rm d}\hat{X}}{{\rm d}\theta}\right\rvert^2 - \hat{\lambda} \dfrac{\partial {f}}{\partial \hat{\boldsymbol{p}}} \lvert \hat{X} \rvert^2 \right)}{\int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta\, {f}\lvert \hat{X}\rvert^2}. \end{equation}
\begin{equation} \frac{\partial \hat{\lambda}}{\partial \hat{\boldsymbol{p}}} = \frac{\int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta \left(\dfrac{\partial {c}}{\partial \hat{\boldsymbol{p}}} \lvert \hat{X}\rvert^2 - \dfrac{\partial {g}}{\partial \hat{\boldsymbol{p}}}\left\lvert \dfrac{{\rm d}\hat{X}}{{\rm d}\theta}\right\rvert^2 - \hat{\lambda} \dfrac{\partial {f}}{\partial \hat{\boldsymbol{p}}} \lvert \hat{X} \rvert^2 \right)}{\int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta\, {f}\lvert \hat{X}\rvert^2}. \end{equation}
To obtain ![]() $\partial \hat {\lambda }/\partial \hat {\boldsymbol {p}}$ using a central-finite-difference scheme, one has to solve the ideal ballooning equation
$\partial \hat {\lambda }/\partial \hat {\boldsymbol {p}}$ using a central-finite-difference scheme, one has to solve the ideal ballooning equation ![]() $2 n_{\hat {\boldsymbol {p}}} = 4$ times at each optimisation step, where
$2 n_{\hat {\boldsymbol {p}}} = 4$ times at each optimisation step, where ![]() $n_{\hat {\boldsymbol {p}}}$ is the length of the vector
$n_{\hat {\boldsymbol {p}}}$ is the length of the vector ![]() $\hat {\boldsymbol {p}}$. However, using the adjoint relation (4.5), we only have to solve it once per optimisation step, as long as we can calculate the gradients of geometry-related quantities
$\hat {\boldsymbol {p}}$. However, using the adjoint relation (4.5), we only have to solve it once per optimisation step, as long as we can calculate the gradients of geometry-related quantities ![]() ${g}$,
${g}$, ![]() ${c}$ and
${c}$ and ![]() ${f}$ four times. Since gradients of
${f}$ four times. Since gradients of ![]() ${g}$,
${g}$, ![]() ${c}$ and
${c}$ and ![]() ${f}$ can be calculated roughly two orders of magnitude faster than solving the ideal ballooning equation, we speed up the gradient calculation by approximately a factor of four. Therefore, we use the adjoint relation (4.5) to calculate the gradient of
${f}$ can be calculated roughly two orders of magnitude faster than solving the ideal ballooning equation, we speed up the gradient calculation by approximately a factor of four. Therefore, we use the adjoint relation (4.5) to calculate the gradient of ![]() $\hat {\lambda }$. In this study, we choose
$\hat {\lambda }$. In this study, we choose
Applying this fact to (4.2) and using (4.5),
 \begin{equation} \frac{{\rm d} \mathcal{H}}{{\rm d}\hat{\boldsymbol{p}}} = \frac{\partial \hat{\lambda}}{\partial \hat{\boldsymbol{p}}} = \frac{\int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta \left(\dfrac{\partial {c}}{\partial \hat{\boldsymbol{p}}} \lvert \hat{X}\rvert^2 - \dfrac{\partial {g}}{\partial \hat{\boldsymbol{p}}}\left\lvert \dfrac{{\rm d}\hat{X}}{{\rm d}\theta}\right\rvert^2 - \hat{\lambda} \dfrac{\partial {f}}{\partial \hat{\boldsymbol{p}}} \lvert \hat{X} \rvert^2 \right)}{\int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta\, {f}\lvert \hat{X}\rvert^2}. \end{equation}
\begin{equation} \frac{{\rm d} \mathcal{H}}{{\rm d}\hat{\boldsymbol{p}}} = \frac{\partial \hat{\lambda}}{\partial \hat{\boldsymbol{p}}} = \frac{\int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta \left(\dfrac{\partial {c}}{\partial \hat{\boldsymbol{p}}} \lvert \hat{X}\rvert^2 - \dfrac{\partial {g}}{\partial \hat{\boldsymbol{p}}}\left\lvert \dfrac{{\rm d}\hat{X}}{{\rm d}\theta}\right\rvert^2 - \hat{\lambda} \dfrac{\partial {f}}{\partial \hat{\boldsymbol{p}}} \lvert \hat{X} \rvert^2 \right)}{\int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta\, {f}\lvert \hat{X}\rvert^2}. \end{equation}
This relation gives us the derivative of the ballooning objective function at any point ![]() $\hat {\boldsymbol {p}} = (\alpha _{t}, \theta _0)$. Note that in this work we use (4.7) combined with a local, gradient-based algorithm to find
$\hat {\boldsymbol {p}} = (\alpha _{t}, \theta _0)$. Note that in this work we use (4.7) combined with a local, gradient-based algorithm to find ![]() $\hat {\lambda }_{\mathrm {max}}$ on a flux surface. However, this method is valid and, under appropriate conditions, can be extended to the equilibrium parameters
$\hat {\lambda }_{\mathrm {max}}$ on a flux surface. However, this method is valid and, under appropriate conditions, can be extended to the equilibrium parameters ![]() $\tilde {\boldsymbol {p}}$. The details of the extended adjoint method are given in Appendix B.1.
$\tilde {\boldsymbol {p}}$. The details of the extended adjoint method are given in Appendix B.1.
In the next section, we present comparison between adjoint and the regular finite-difference-based methods and present tests comparing the gradients of ![]() $\hat {\lambda }$ from these two methods.
$\hat {\lambda }$ from these two methods.
4.1. Comparing adjoint gradients with a finite-difference method
In this section, we first compare the values of the gradients of ![]() $\hat {\lambda }_{\mathrm {max}}$ from the adjoint method with their values obtained using a central-finite-difference method. We take a typical optimisation loop in the modified NCSX case and show a gradient comparison in figure 4. As you can see, the gradients obtained using an adjoint method match well with the gradients obtained with a finite-difference method.
$\hat {\lambda }_{\mathrm {max}}$ from the adjoint method with their values obtained using a central-finite-difference method. We take a typical optimisation loop in the modified NCSX case and show a gradient comparison in figure 4. As you can see, the gradients obtained using an adjoint method match well with the gradients obtained with a finite-difference method.

Figure 4. (a) Comparison between the gradients of eigenvalue ![]() $\hat {\lambda }_{\alpha _{t}} = \partial \hat {\lambda }/\partial \alpha _{t}$ and
$\hat {\lambda }_{\alpha _{t}} = \partial \hat {\lambda }/\partial \alpha _{t}$ and ![]() $\hat {\lambda }_{\theta _0} = \partial \hat {\lambda }/\partial \theta _0$ obtained using a finite-difference scheme against those obtained using an adjoint method. The quantity
$\hat {\lambda }_{\theta _0} = \partial \hat {\lambda }/\partial \theta _0$ obtained using a finite-difference scheme against those obtained using an adjoint method. The quantity ![]() $\mathrm {iter}$ is the number of iterations taken by the local optimiser on a flux surface before finding
$\mathrm {iter}$ is the number of iterations taken by the local optimiser on a flux surface before finding ![]() $\hat {\lambda }_{\mathrm {max}}$. The gradients match well for around four orders of magnitude. The discrepancy between the adjoint and finite difference
$\hat {\lambda }_{\mathrm {max}}$. The gradients match well for around four orders of magnitude. The discrepancy between the adjoint and finite difference ![]() $\hat {\lambda }_{\alpha _{t}}$ is due to the finite resolution of the
$\hat {\lambda }_{\alpha _{t}}$ is due to the finite resolution of the ![]() $\texttt {VMEC}$ run. (b) Different grids used to calculate the gradient of the eigenvalue
$\texttt {VMEC}$ run. (b) Different grids used to calculate the gradient of the eigenvalue ![]() $\hat {\lambda }$ on a flux surface. A finite-difference scheme requires four points, whereas an adjoint method only requires one point. This gives us a four times speed-up.
$\hat {\lambda }$ on a flux surface. A finite-difference scheme requires four points, whereas an adjoint method only requires one point. This gives us a four times speed-up.
To show the computational speedup, we also compare the time taken by an adjoint method with the regular finite-difference-based method. For the 30 iterations shown in figure 4(a), the adjoint method was about ![]() $4$ times faster than the finite-difference method. Indeed, the most expensive part of the gradient calculation is the ballooning solver. As shown in the illustration in figure 4(b), for a second-order accurate central-difference scheme, an adjoint method only needs a single call to the ballooning solver, whereas the finite-difference solver needs four. In principle, a speed-up factor of up to four should be possible.
$4$ times faster than the finite-difference method. Indeed, the most expensive part of the gradient calculation is the ballooning solver. As shown in the illustration in figure 4(b), for a second-order accurate central-difference scheme, an adjoint method only needs a single call to the ballooning solver, whereas the finite-difference solver needs four. In principle, a speed-up factor of up to four should be possible.
5. Details of the optimisation process
In this section, we explain the optimisation process to find equilibria that are stable against the ideal ballooning mode. In § 5.1, we describe the process of using an adjoint method to find the maximum eigenvalue ![]() $\hat {\lambda }_{\mathrm {max}}$ on each flux surface. In § 5.2, we explain how we use
$\hat {\lambda }_{\mathrm {max}}$ on each flux surface. In § 5.2, we explain how we use ![]() $\hat {\lambda }_{\mathrm {max}}$ and other penalty terms to construct the overall objective function
$\hat {\lambda }_{\mathrm {max}}$ and other penalty terms to construct the overall objective function ![]() $\mathcal {F}$. Finally, in § 5.3, we explain how we search for ballooning stable equilibria while minimising
$\mathcal {F}$. Finally, in § 5.3, we explain how we search for ballooning stable equilibria while minimising ![]() $\mathcal {F}$ using the SIMSOPT framework.
$\mathcal {F}$ using the SIMSOPT framework.
5.1. Finding  $\hat {\lambda }_{\mathrm {max}}$ on each flux surface
$\hat {\lambda }_{\mathrm {max}}$ on each flux surface
To calculate the ballooning objective function we find the maximum ![]() $\hat {\lambda }$ on each flux surface. To do that, we solve (3.3) on several flux surfaces, multiple field lines on each surface and numerous values of
$\hat {\lambda }$ on each flux surface. To do that, we solve (3.3) on several flux surfaces, multiple field lines on each surface and numerous values of ![]() $\theta _0$ on each field line. We calculate
$\theta _0$ on each field line. We calculate ![]() $\hat {\lambda }_{\mathrm {max}}$ on
$\hat {\lambda }_{\mathrm {max}}$ on ![]() $\mathrm {ns} = 16$ flux surfaces for each equilibrium. For the 3D equilibria, we scan
$\mathrm {ns} = 16$ flux surfaces for each equilibrium. For the 3D equilibria, we scan ![]() $n_{\alpha _{t}} = 42$ field lines in the range
$n_{\alpha _{t}} = 42$ field lines in the range ![]() $\alpha _{t} = [-{\rm \pi}, {\rm \pi})$. Since all field lines are identical in a 2D axisymmetric equilibrium, we scan only one field line, i.e.
$\alpha _{t} = [-{\rm \pi}, {\rm \pi})$. Since all field lines are identical in a 2D axisymmetric equilibrium, we scan only one field line, i.e.![]() $n_{\alpha } = 1$ for the 2D equilibrium. On each field line, we scan
$n_{\alpha } = 1$ for the 2D equilibrium. On each field line, we scan ![]() $n_{\theta _0} = 21$ values of
$n_{\theta _0} = 21$ values of ![]() $\theta _0$ in the range
$\theta _0$ in the range ![]() $\theta _0 = [-{\rm \pi} /2, {\rm \pi}/2)$. The maximum
$\theta _0 = [-{\rm \pi} /2, {\rm \pi}/2)$. The maximum ![]() $\hat {\lambda }$ from a coarse grid scan gives us a value close to the global maximum. From the maximum
$\hat {\lambda }$ from a coarse grid scan gives us a value close to the global maximum. From the maximum ![]() $\hat {\lambda }$ of the coarse grid, we launch a local gradient-based optimiser to find the global maximum eigenvalue. This process is explained using the illustration figure 5. Using this process, we obtain
$\hat {\lambda }$ of the coarse grid, we launch a local gradient-based optimiser to find the global maximum eigenvalue. This process is explained using the illustration figure 5. Using this process, we obtain ![]() $\hat {\lambda }_{\mathrm {max}}$ as a function of the normalised toroidal flux
$\hat {\lambda }_{\mathrm {max}}$ as a function of the normalised toroidal flux ![]() $s$. Figure 6 shows the plot of
$s$. Figure 6 shows the plot of ![]() $\hat {\lambda }_{\mathrm {max}}$ against
$\hat {\lambda }_{\mathrm {max}}$ against ![]() $s$ for the three chosen equilibria.
$s$ for the three chosen equilibria.

Figure 5. Process of finding the globally maximum eigenvalue ![]() $\hat {\lambda }_{\mathrm {max}}$ on the flux surface
$\hat {\lambda }_{\mathrm {max}}$ on the flux surface ![]() $s = 0.8$ of the NCSX equilibrium. We start by first finding the maximum
$s = 0.8$ of the NCSX equilibrium. We start by first finding the maximum ![]() $\hat {\lambda }$ on a discrete grid (marked by crosses) of
$\hat {\lambda }$ on a discrete grid (marked by crosses) of ![]() $\alpha _{t}$ and
$\alpha _{t}$ and ![]() $\theta _0$. From the discrete maximum
$\theta _0$. From the discrete maximum ![]() $\hat {\lambda }$, we search for the global maximum eigenvalue using a local optimiser. In the inset, we show the approximate path taken by the optimiser to reach
$\hat {\lambda }$, we search for the global maximum eigenvalue using a local optimiser. In the inset, we show the approximate path taken by the optimiser to reach ![]() $\hat {\lambda }_{\mathrm {max}}$. This process is repeated for all the flux surfaces.
$\hat {\lambda }_{\mathrm {max}}$. This process is repeated for all the flux surfaces.

Figure 6. Plots of ![]() $\hat {\lambda }_{\mathrm {max}}$ against the normalised toroidal flux
$\hat {\lambda }_{\mathrm {max}}$ against the normalised toroidal flux ![]() $s$ for the three chosen equilibria in (a–c) and the eigenfunctions
$s$ for the three chosen equilibria in (a–c) and the eigenfunctions ![]() $\hat {X}$ at the maximum
$\hat {X}$ at the maximum ![]() $\hat {\lambda }_\textrm {max}$ for each equilibrium in the (d–f): (a) DIII-D
$\hat {\lambda }_\textrm {max}$ for each equilibrium in the (d–f): (a) DIII-D ![]() $\hat {\lambda }_\textrm {max}$, (b) NCSX
$\hat {\lambda }_\textrm {max}$, (b) NCSX ![]() $\hat {\lambda }_\textrm {max}$, (c) Henneberg-QA
$\hat {\lambda }_\textrm {max}$, (c) Henneberg-QA ![]() $\hat {\lambda }_\textrm {max}$, (d) DIII-D
$\hat {\lambda }_\textrm {max}$, (d) DIII-D ![]() $\hat {X}(s = 0.95)$, (e) NCSX
$\hat {X}(s = 0.95)$, (e) NCSX ![]() $\hat {X}(s = 0.8)$ and( f) Henneberg-QA
$\hat {X}(s = 0.8)$ and( f) Henneberg-QA![]() $\hat {X}(s = 0.84)$. The decay of the eigenfunction could be a result of the Anderson localisation of ballooning modes, as discussed by Redi et al. (Reference Redi, Johnson, Klasky, Canik, Dewar and Cooper2002).
$\hat {X}(s = 0.84)$. The decay of the eigenfunction could be a result of the Anderson localisation of ballooning modes, as discussed by Redi et al. (Reference Redi, Johnson, Klasky, Canik, Dewar and Cooper2002).
For each new equilibrium, on all ![]() $\mathrm {ns}=16$ flux surfaces, the local optimiser takes an average of
$\mathrm {ns}=16$ flux surfaces, the local optimiser takes an average of ![]() $20$ iterations to find
$20$ iterations to find ![]() $\hat {\lambda }_{\mathrm {max}}$. Moreover, as described in figure 4(b), at each step, the use of a finite-difference method requires four evaluations of the eigenvalue
$\hat {\lambda }_{\mathrm {max}}$. Moreover, as described in figure 4(b), at each step, the use of a finite-difference method requires four evaluations of the eigenvalue ![]() $\hat {\lambda }$. This means that on average, we have to call the ballooning solver
$\hat {\lambda }$. This means that on average, we have to call the ballooning solver ![]() $1280$ (
$1280$ (![]() $16 \times 20 \times 4$) times. This is a computationally expensive step that we speed up using our adjoint-based method.
$16 \times 20 \times 4$) times. This is a computationally expensive step that we speed up using our adjoint-based method.
5.2. Finding ballooning-stable equilibria
Once we have found ![]() $\hat {\lambda }_{\mathrm {max}}$, we seek an equilibrium stable to the ideal ballooning mode by minimising
$\hat {\lambda }_{\mathrm {max}}$, we seek an equilibrium stable to the ideal ballooning mode by minimising ![]() $\hat {\lambda }_{\mathrm {max}}$ on each flux surface. To do so, we need to define an objective function that depends on
$\hat {\lambda }_{\mathrm {max}}$ on each flux surface. To do so, we need to define an objective function that depends on ![]() $\hat {\lambda }_{\mathrm {max}}$ such that minimising the objective function should allow us to achieve a stable equilibrium. Moreover, during optimisation, once a flux surface is stabilised against the ideal ballooning mode, our objective function should ignore that particular surface. This would be useful as we do not want to penalise a stable equilibrium. To this end, we design the following ideal ballooning objective function
$\hat {\lambda }_{\mathrm {max}}$ such that minimising the objective function should allow us to achieve a stable equilibrium. Moreover, during optimisation, once a flux surface is stabilised against the ideal ballooning mode, our objective function should ignore that particular surface. This would be useful as we do not want to penalise a stable equilibrium. To this end, we design the following ideal ballooning objective function
 \begin{equation} f_{\mathrm{ball}} = \sum_{j=1}^{\mathrm{ns}} \mathrm{ReLU}(\hat{\lambda}_{\mathrm{max},j} - \hat{\lambda}_{\mathrm{th}, j}), \end{equation}
\begin{equation} f_{\mathrm{ball}} = \sum_{j=1}^{\mathrm{ns}} \mathrm{ReLU}(\hat{\lambda}_{\mathrm{max},j} - \hat{\lambda}_{\mathrm{th}, j}), \end{equation}
where ![]() $\mathrm {ns}$ is the total number of surfaces and
$\mathrm {ns}$ is the total number of surfaces and
 \begin{equation} \mathrm{ReLU}(x)= \begin{cases} 0, & \text{if } x\leq 0,\\ x, & x> 0, \end{cases} \end{equation}
\begin{equation} \mathrm{ReLU}(x)= \begin{cases} 0, & \text{if } x\leq 0,\\ x, & x> 0, \end{cases} \end{equation}
is the rectified linear unit operator: an operator that sets all the non-positive values to zero and ![]() $\hat {\lambda }_{\mathrm {th},j}$ is the threshold below which we declare a surface ideal ballooning stable. The value
$\hat {\lambda }_{\mathrm {th},j}$ is the threshold below which we declare a surface ideal ballooning stable. The value ![]() $\hat {\lambda }_{j} = 0$ on the
$\hat {\lambda }_{j} = 0$ on the ![]() $j$th surface implies marginal stability but we choose
$j$th surface implies marginal stability but we choose ![]() $\hat {\lambda }_{\mathrm {th},j} = 0.0001$ to ensure that all surfaces are slightly away from marginal ideal ballooning stability. An equilibrium is ideal ballooning stable if
$\hat {\lambda }_{\mathrm {th},j} = 0.0001$ to ensure that all surfaces are slightly away from marginal ideal ballooning stability. An equilibrium is ideal ballooning stable if ![]() $f_{\mathrm {ball}} = 0$.
$f_{\mathrm {ball}} = 0$.
It is also important to prevent the optimiser from minimising ![]() $f_{\mathrm {ball}}$ in a trivial way. For example, for 2D equilibria, going to a larger aspect ratio value stabilises the ideal ballooning mode. For 3D equilibria, the optimiser can sometimes reduce the minor radius, which, for a fixed toroidal flux, causes the magnetic field to increase. This lowers the overall
$f_{\mathrm {ball}}$ in a trivial way. For example, for 2D equilibria, going to a larger aspect ratio value stabilises the ideal ballooning mode. For 3D equilibria, the optimiser can sometimes reduce the minor radius, which, for a fixed toroidal flux, causes the magnetic field to increase. This lowers the overall ![]() $\beta$ and consequently the unstable curvature drive term. Similarly, if we allow rotational transforms to increase freely, the optimiser can sometimes create large gradients of
$\beta$ and consequently the unstable curvature drive term. Similarly, if we allow rotational transforms to increase freely, the optimiser can sometimes create large gradients of ![]() $\iota$, generating large currents which are suboptimal. To avoid achieving such trivial solutions and uninteresting equilibria, we add a combination of the following penalty terms to the optimiser:
$\iota$, generating large currents which are suboptimal. To avoid achieving such trivial solutions and uninteresting equilibria, we add a combination of the following penalty terms to the optimiser:
(i)
 $f_{\mathrm {asp}} = (A - A_0)$ to penalise any deviation from the aspect ratio of the initial equilibrium;
$f_{\mathrm {asp}} = (A - A_0)$ to penalise any deviation from the aspect ratio of the initial equilibrium;(ii)
 $f_{\mathrm {minr}} = (a_{N} - a_{{N}0})$ to penalise any deviation from the minor radius of the initial equilibrium;
$f_{\mathrm {minr}} = (a_{N} - a_{{N}0})$ to penalise any deviation from the minor radius of the initial equilibrium;(iii)
 $f_{\langle B \rangle } = (\langle B \rangle - \langle B\rangle _0)$ to penalise any deviation of the volume-averaged magnetic field from its value in the initial equilibrium;
$f_{\langle B \rangle } = (\langle B \rangle - \langle B\rangle _0)$ to penalise any deviation of the volume-averaged magnetic field from its value in the initial equilibrium;(iv)
 $f_{R_{c}} = \int \,\textrm {d}\theta \, \mathrm {ReLU}({-R_{c}})$, where
$f_{R_{c}} = \int \,\textrm {d}\theta \, \mathrm {ReLU}({-R_{c}})$, where  $R_{c}$ is the radius of curvature of the boundary; this term penalises any boundary shapes that are curved into the plasma
$R_{c}$ is the radius of curvature of the boundary; this term penalises any boundary shapes that are curved into the plasma
Using the ballooning objective function (5.1) and one or more of the penalty terms described previously, we can get the overall objective function ![]() $\mathcal {F}$. Given a vector of input parameters
$\mathcal {F}$. Given a vector of input parameters ![]() $\boldsymbol {p}$, our goal is to solve
$\boldsymbol {p}$, our goal is to solve
We achieve this with the help of the ![]() $\texttt {SIMSOPT}$ (Landreman et al. Reference Landreman, Medasani, Wechsung, Giuliani, Jorge and Zhu2021) package. The implementation details of the optimisation are described in the next subsection.
$\texttt {SIMSOPT}$ (Landreman et al. Reference Landreman, Medasani, Wechsung, Giuliani, Jorge and Zhu2021) package. The implementation details of the optimisation are described in the next subsection.
5.3. Optimisation with the  $\mathtt {SIMSOPT}$ package
$\mathtt {SIMSOPT}$ package
In this subsection, we discuss the implementation-related details of an adjoint ballooning solver with the SIMSOPT (Landreman et al. Reference Landreman, Medasani, Wechsung, Giuliani, Jorge and Zhu2021) package. First, we briefly explain how an optimisation problem can be solved using SIMSOPT. Next, we go into the details of how we solve the ideal ballooning optimisation and how the use of an adjoint method can speed up this process.
The SIMSOPT package is a optimisation framework containing a suite of codes that, along with the ![]() $\texttt {VMEC}$ code, have been used to optimise3D equilibria for various properties such as energetic fast-particle confinement, quasisymmetry, simpler magnetic coil geometry and neoclassical transport. The user specifies the input parameters (also referred to as degrees of freedom (DoFs)) and the objective function
$\texttt {VMEC}$ code, have been used to optimise3D equilibria for various properties such as energetic fast-particle confinement, quasisymmetry, simpler magnetic coil geometry and neoclassical transport. The user specifies the input parameters (also referred to as degrees of freedom (DoFs)) and the objective function ![]() $\mathcal {F}$ and
$\mathcal {F}$ and ![]() $\texttt {SIMSOPT}$ can perform a gradient-based or gradient-free nonlinear least squares optimisation.
$\texttt {SIMSOPT}$ can perform a gradient-based or gradient-free nonlinear least squares optimisation.
As an example, let us construct an optimisation problem to stabilise an equilibrium while penalising the change in the aspect ratio and the minor radius of the boundary
To do so, we use gradient-based optimisation in SIMSOPT, where one calculates ![]() $\partial \mathcal {F}/\partial \boldsymbol {p}$ to update the parameter vector at the
$\partial \mathcal {F}/\partial \boldsymbol {p}$ to update the parameter vector at the ![]() $i$th iteration,
$i$th iteration, ![]() $\boldsymbol {p}_i$ as
$\boldsymbol {p}_i$ as
This is done until the optimiser reaches a local minima, i.e.a region in the parameter space where ![]() $\partial \mathcal {F}/\partial \boldsymbol {p} = 0$ or the relative change in the gradient is small enough. Typically, one has to evaluate the gradient of
$\partial \mathcal {F}/\partial \boldsymbol {p} = 0$ or the relative change in the gradient is small enough. Typically, one has to evaluate the gradient of ![]() $\mathcal {F}$ hundreds of times during an optimisation loop before finding a local minimum. In this study, evaluating
$\mathcal {F}$ hundreds of times during an optimisation loop before finding a local minimum. In this study, evaluating ![]() $f_{\mathrm {ball}}$ is the most expensive step. Because the speed of the optimisation is limited by the rate at which we can compute
$f_{\mathrm {ball}}$ is the most expensive step. Because the speed of the optimisation is limited by the rate at which we can compute ![]() $f_{\mathrm {ball}}$, we have used an adjoint method to calculate
$f_{\mathrm {ball}}$, we have used an adjoint method to calculate ![]() $\hat {\lambda }_{\mathrm {max}}$ which gives us
$\hat {\lambda }_{\mathrm {max}}$ which gives us ![]() $f_{\mathrm {ball}}$.
$f_{\mathrm {ball}}$.
6. Results
In this section, we present the results of our study. In § 6.1, we compare the initial and optimised 2D axisymmetric equilibrium. In §§ 6.2 and 6.3, we do the same for the modified NCSX and modified Henneberg-QA equilibria, respectively. We also compare the values of relevant physical quantities in the initial and optimised equilibria.
6.1. Stabilising the DIII-D-like equilibrium
For the 2D axisymmetric case, we start with a high-![]() $\beta$ equilibrium with a negative triangularity boundary. Due to axisymmetry, the 2D boundary does not depend on the toroidal angle
$\beta$ equilibrium with a negative triangularity boundary. Due to axisymmetry, the 2D boundary does not depend on the toroidal angle ![]() $\zeta$. In other words, only
$\zeta$. In other words, only ![]() $n = 0$ are needed in (2.7) to represent the boundary of a 2D equilibrium. Therefore, the number of modes needed to specify a 2D boundary is much lower than that for a typical 3D boundary. In this problem, we pick the six largest Fourier modes as our DoFs:
$n = 0$ are needed in (2.7) to represent the boundary of a 2D equilibrium. Therefore, the number of modes needed to specify a 2D boundary is much lower than that for a typical 3D boundary. In this problem, we pick the six largest Fourier modes as our DoFs: ![]() $\hat {R}_{b}(0, 1), \hat {R}_{b}(0, 2), \hat {R}_{b}(0, 3), \hat {Z}_{b}(0, 1), \hat {Z}_{b}(0, 3), \hat {Z}_{b}(0, 5)$. The full objective function is
$\hat {R}_{b}(0, 1), \hat {R}_{b}(0, 2), \hat {R}_{b}(0, 3), \hat {Z}_{b}(0, 1), \hat {Z}_{b}(0, 3), \hat {Z}_{b}(0, 5)$. The full objective function is
where all terms except ![]() $f_{\mathrm {ball}}$ are penalty terms to prevent the optimiser from producing a trivial solution. After this, we start with the negative triangularity equilibrium described in § 2.2 and run SIMSOPT to find multiple equilibria that are stable against the ideal ballooning mode, i.e. equilibria with
$f_{\mathrm {ball}}$ are penalty terms to prevent the optimiser from producing a trivial solution. After this, we start with the negative triangularity equilibrium described in § 2.2 and run SIMSOPT to find multiple equilibria that are stable against the ideal ballooning mode, i.e. equilibria with ![]() $f_{\mathrm {ball}} = 0$. We present one of the optimised equilibria in figure 7. We also compare the values of equilibrium-dependent quantities in table 4.
$f_{\mathrm {ball}} = 0$. We present one of the optimised equilibria in figure 7. We also compare the values of equilibrium-dependent quantities in table 4.

Figure 7. (a) Maximum eigenvalue ![]() $\hat {\lambda }_{\mathrm {max}}$ of the initial and optimised DIII-D-like equilibrium. The optimised equilibrium is stable. (b) Boundary shape of the initial and final equilibria. Note the negative triangularity of the initial equilibrium and the positive triangularity of the optimised equilibrium.
$\hat {\lambda }_{\mathrm {max}}$ of the initial and optimised DIII-D-like equilibrium. The optimised equilibrium is stable. (b) Boundary shape of the initial and final equilibria. Note the negative triangularity of the initial equilibrium and the positive triangularity of the optimised equilibrium.
Table 4. Comparison between relevant physical quantities of the initial and optimised DIII-D equilibrium.

We observe that the optimiser is moving toward a positive triangularity equilibrium, indicating that, for the similar values of the relevant parameters (given in table 4) positive triangularity high-![]() $\beta$ equilibria are more stable than their negative triangularity counterparts. Our findings are consistent with recent observations by Davies, Dickinson & Wilson (Reference Davies, Dickinson and Wilson2022), Nelson, Paz-Soldan & Saarelma (Reference Nelson, Paz-Soldan and Saarelma2022) and Saarelma et al. (Reference Saarelma, Austin, Knolker, Marinoni, Paz-Soldan, Schmitz and Snyder2021) that negative triangularity equilibria are more unstable against the ideal ballooning mode compared with positive triangularity equilibria. This behaviour prevents the formation of a steep pressure gradient, which limits the operational beta value of negative triangularity equilibria but also prevents the occurrence of edge localisedmodes.
$\beta$ equilibria are more stable than their negative triangularity counterparts. Our findings are consistent with recent observations by Davies, Dickinson & Wilson (Reference Davies, Dickinson and Wilson2022), Nelson, Paz-Soldan & Saarelma (Reference Nelson, Paz-Soldan and Saarelma2022) and Saarelma et al. (Reference Saarelma, Austin, Knolker, Marinoni, Paz-Soldan, Schmitz and Snyder2021) that negative triangularity equilibria are more unstable against the ideal ballooning mode compared with positive triangularity equilibria. This behaviour prevents the formation of a steep pressure gradient, which limits the operational beta value of negative triangularity equilibria but also prevents the occurrence of edge localisedmodes.
6.2. Stabilising the NCSX equilibrium
The first 3D equilibrium we optimise is an unstable NCSX equilibrium. Since the boundary has a 3D shape, we have to use both toroidal and poloidal modes to change its shape. For this demonstration, we choose ![]() $72$ boundary modes listed in table 5 as DoFs. In table 5,
$72$ boundary modes listed in table 5 as DoFs. In table 5, ![]() $[i, j]$ denotes all integers between
$[i, j]$ denotes all integers between ![]() $i$ and
$i$ and ![]() $j$ (including
$j$ (including ![]() $i$ and
$i$ and ![]() $j$). The total number of DoFs,
$j$). The total number of DoFs, ![]() $72$, is much larger than the axisymmetric case. After choosing these DoFs, we choose the following objective function
$72$, is much larger than the axisymmetric case. After choosing these DoFs, we choose the following objective function
We run SIMSOPT with this configuration to obtain multiple equilibria with ![]() $f_{\mathrm {ball}} = 0$. We have plotted a comparison of one of these equilibria with the initial equilibrium in figure 8.
$f_{\mathrm {ball}} = 0$. We have plotted a comparison of one of these equilibria with the initial equilibrium in figure 8.
Table 5. Boundary shape DoFs for the NCSX case.


Figure 8. (a) Maximum eigenvalue ![]() $\hat {\lambda }_{\mathrm {max}}$ of the initial and optimised modified NCSX equilibrium. (b) Boundary shape of the initial and final equilibria at three different values of the toroidal angle
$\hat {\lambda }_{\mathrm {max}}$ of the initial and optimised modified NCSX equilibrium. (b) Boundary shape of the initial and final equilibria at three different values of the toroidal angle ![]() $\zeta$. The dotted curves correspond to the initial cross sections whereas the solid curves are the final cross sections. Note how sensitive the maximum eigenvalue is to the boundary shape.
$\zeta$. The dotted curves correspond to the initial cross sections whereas the solid curves are the final cross sections. Note how sensitive the maximum eigenvalue is to the boundary shape.
The optimiser successfully stabilised the equilibrium through boundary shaping. From the change in the boundary shape, it is evident that the ideal ballooning stability is sensitive to the boundary shape for the NCSX equilibrium. We present a comparison of the important equilibrium-dependent quantities for the initial and optimised equilibria in table 6.
Table 6. Comparison between relevant physical quantities of the initial and optimised NCSX equilibrium.

6.3. Stabilising the modified Henneberg-QA equilibrium
As a final example, we present a modified Henneberg-QA equilibrium. In this example, we allow the boundary coefficients given in table 7 to change freely.
Table 7. Boundary shape DoFs for the modified Henneberg-QA case. We have chosen the exact same coefficients as the NCSX case.

For this problem, we choose the following objective function
After choosing the DoFs and the objective function, we run SIMSOPT and obtain multiple stable equilibria. We compare the stabilisedequilibrium with the initial, unstable equilibrium in figure 9 and the equilibrium-dependent quantities in table 8. We can see in figure 9(a) that the boundary shape deforms in a way to reduce the curvature on the outboard side, stabilising the ideal ballooning mode.

Figure 9. (a) Maximum eigenvalue ![]() $\hat {\lambda }_{\mathrm {max}}$ of the initial and optimised modified Henneberg-QA equilibrium. (b) Boundary shape of the initial and final equilibria at three different positions of the toroidal angle
$\hat {\lambda }_{\mathrm {max}}$ of the initial and optimised modified Henneberg-QA equilibrium. (b) Boundary shape of the initial and final equilibria at three different positions of the toroidal angle ![]() $\zeta$. The dotted curves correspond to the initial cross sections whereas the solid curves are the final cross sections.
$\zeta$. The dotted curves correspond to the initial cross sections whereas the solid curves are the final cross sections.
Table 8. Comparison between relevant physical quantities of the initial and optimised modified Henneberg-QA equilibrium.

7. Summary and conclusions
We began this work by briefly explaining the various curvilinear coordinate systems that we used to fully define a general 3D ideal MHD equilibrium. In § 2, we generated three different equilibria, one axisymmetric 2D and two 3D, and briefly described their properties.
Upon generating the equilibria, in § 3, we have provided a physical description of the infinite-![]() $n$ ideal ballooning mode and explain the numerical methods used to calculate the maximum eigenvalues on a given flux surface. Using these numerical methods, we evaluated the stability of the three equilibria against the ideal ballooning mode. We also described the self-adjoint property of the ideal ballooning mode and its relation to the KBM.
$n$ ideal ballooning mode and explain the numerical methods used to calculate the maximum eigenvalues on a given flux surface. Using these numerical methods, we evaluated the stability of the three equilibria against the ideal ballooning mode. We also described the self-adjoint property of the ideal ballooning mode and its relation to the KBM.
Using the self-adjoint property explained in § 3, we have developed an adjoint method in § 4 and explained how to use it to speed up the calculation of the maximum ballooning eigenvalue ![]() $\hat {\lambda }_{\mathrm {max}}$ on each surface. To demonstrate the efficiency and accuracy of the adjoint method, we have also presented a comparison of gradients between an adjoint method and a simple finite-difference scheme. We found that the adjoint method is up to four times faster than the finite-difference scheme.
$\hat {\lambda }_{\mathrm {max}}$ on each surface. To demonstrate the efficiency and accuracy of the adjoint method, we have also presented a comparison of gradients between an adjoint method and a simple finite-difference scheme. We found that the adjoint method is up to four times faster than the finite-difference scheme.
In § 5, we describe the details of the overall optimisation process and how we accomplish that using the SIMSOPT code. After implementing the optimisation, we presented the results in § 6. We have presented the specific details of the objective function and the DoFs for each equilibrium and stabilised the initial, ideal ballooning unstable equilibria. We have briefly described the physical mechanisms that stabilise the ideal ballooning mode.
This work presents many avenues for future research. A key step forward is to extend our technique to include all equilibrium-dependent parameters ![]() $\tilde {\boldsymbol {p}}$ as explained in Appendix B.1. One could also use the exact same method to optimise stellarators and tokamaks against low-
$\tilde {\boldsymbol {p}}$ as explained in Appendix B.1. One could also use the exact same method to optimise stellarators and tokamaks against low-![]() $n$, unstable ideal MHD modes, as explained in Appendix B.2. Since solving for low-
$n$, unstable ideal MHD modes, as explained in Appendix B.2. Since solving for low-![]() $n$ ideal MHD codes is much more computationally expensive, the advantage of using an adjoint method would be even greater. Another possible direction would be to use an adjoint method to get derivatives of the ballooning eigenvalue with respect to the plasma shape. Finally, one could use the ideal ballooning optimiser as a tool that could help optimise an equilibrium against KBMs and help us look for equilibrium-dependent proxies for MHD or kinetic instabilities.
$n$ ideal MHD codes is much more computationally expensive, the advantage of using an adjoint method would be even greater. Another possible direction would be to use an adjoint method to get derivatives of the ballooning eigenvalue with respect to the plasma shape. Finally, one could use the ideal ballooning optimiser as a tool that could help optimise an equilibrium against KBMs and help us look for equilibrium-dependent proxies for MHD or kinetic instabilities.
Acknowledgements
We thank Professor D. Bindel, Dr A. Bader and Dr B. Faber for helpful discussions and encouragement. R.G. thanks R. Conlin for his valuable suggestions at the APS-DPP 2022 conference.
Editor P. Helander thanks the referees for their advice in evaluating this article.
Funding
This work was supported by the US Department of Energy, Office of Science and Office of Fusion Energy Sciences under award numbers DE-SC0018429 and DE-FG02-93ER54197. This research used resources from the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility and the Stellar cluster at Princeton University. This material is based on work supported by the National Science Foundation Graduate Research Fellowship under grant numberDGE-1650441.
Declaration of interests
The authors report no conflict of interest.
Data availability statement
The Zenodo link containing all the equilibria and optimisation code used in this paper is freely available at https://zenodo.org/record/8092287.
Appendix A. The discretised ideal ballooning equation
After applying the boundary conditions ![]() $\hat {X}_0 = \hat {X}_N = 0$ to (3.5), we can rewrite the ballooning equation as
$\hat {X}_0 = \hat {X}_N = 0$ to (3.5), we can rewrite the ballooning equation as
with ![]() $\mathbb {I}$ being the identity matrix and the asymmetric tridiagonal matrix
$\mathbb {I}$ being the identity matrix and the asymmetric tridiagonal matrix ![]() $\boldsymbol{\mathsf{A}}$ with the following form:
$\boldsymbol{\mathsf{A}}$ with the following form:
 \begin{align}
\left[\begin{matrix} \dfrac{{g}_{1/2} + {g}_{3/2} - (\Delta \theta)^2 {c}_{1}}{(\Delta \theta)^2 {f}_{1}} &
-\dfrac{{g}_{3/2}}{(\Delta \theta)^2 {f}_1} & 0 & 0 & \ldots\\
-\dfrac{{g}_{3/2}}{(\Delta \theta)^2 {f}_2} & \dfrac{{g}_{3/2} + {g}_{5/2} - (\Delta \theta)^2 {c}_{2}}{(\Delta \theta)^2 {f}_{2}} &
-\dfrac{{g}_{5/2}}{(\Delta \theta)^2 {f}_2} & 0 & \ldots\\
& & & \ddots\\
& & & & \ddots\\
0 & 0 & 0 & 0 & \ldots\\
0 & 0 & 0 & 0 & \ldots\\
\end{matrix}\right.\nonumber\\
\left.\begin{matrix}
0 & 0\\
0 & 0\\
\vdots&\vdots & \\
\vdots&\vdots & \\
\dfrac{{g}_{N-5/2} + {g}_{N-3/2} - (\Delta \theta)^2 {c}_{N-2}}{h^2 {f}_{N-2}} &
-\dfrac{{g}_{N-3/2}}{(\Delta \theta)^2 {f}_{N-2}}\\
-\dfrac{{g}_{N-3/2}}{(\Delta \theta)^2 {f}_{N-1}} & \dfrac{{g}_{N-3/2} + {g}_{N-1/2} - (\Delta
\theta)^2 {c}_{N-1}}{(\Delta \theta)^2 {f}_{N-1}}\\
\end{matrix}\right]
. \end{align}
\begin{align}
\left[\begin{matrix} \dfrac{{g}_{1/2} + {g}_{3/2} - (\Delta \theta)^2 {c}_{1}}{(\Delta \theta)^2 {f}_{1}} &
-\dfrac{{g}_{3/2}}{(\Delta \theta)^2 {f}_1} & 0 & 0 & \ldots\\
-\dfrac{{g}_{3/2}}{(\Delta \theta)^2 {f}_2} & \dfrac{{g}_{3/2} + {g}_{5/2} - (\Delta \theta)^2 {c}_{2}}{(\Delta \theta)^2 {f}_{2}} &
-\dfrac{{g}_{5/2}}{(\Delta \theta)^2 {f}_2} & 0 & \ldots\\
& & & \ddots\\
& & & & \ddots\\
0 & 0 & 0 & 0 & \ldots\\
0 & 0 & 0 & 0 & \ldots\\
\end{matrix}\right.\nonumber\\
\left.\begin{matrix}
0 & 0\\
0 & 0\\
\vdots&\vdots & \\
\vdots&\vdots & \\
\dfrac{{g}_{N-5/2} + {g}_{N-3/2} - (\Delta \theta)^2 {c}_{N-2}}{h^2 {f}_{N-2}} &
-\dfrac{{g}_{N-3/2}}{(\Delta \theta)^2 {f}_{N-2}}\\
-\dfrac{{g}_{N-3/2}}{(\Delta \theta)^2 {f}_{N-1}} & \dfrac{{g}_{N-3/2} + {g}_{N-1/2} - (\Delta
\theta)^2 {c}_{N-1}}{(\Delta \theta)^2 {f}_{N-1}}\\
\end{matrix}\right]
. \end{align}
Appendix B. Details of the adjoint ideal ballooning calculation
In this appendix, we derive (4.5) starting with (3.3). To do that, we use the self-adjoint property of ideal MHD given in (3.12) as well as the Dirichlet boundary conditions satisfied by the eigenfunction,
Defining ![]() $\boldsymbol {p} = (\tilde {\boldsymbol {p}}, \hat {\boldsymbol {p}})$ as the union of all the parameters of the problem, we start by taking the derivative
$\boldsymbol {p} = (\tilde {\boldsymbol {p}}, \hat {\boldsymbol {p}})$ as the union of all the parameters of the problem, we start by taking the derivative ![]() $\partial /\partial \boldsymbol {p}$ of (3.3),
$\partial /\partial \boldsymbol {p}$ of (3.3),
Multiplying with ![]() $\hat {X}^{*}$ on both sides, integrating throughout the domain,
$\hat {X}^{*}$ on both sides, integrating throughout the domain,
 $$\begin{gather} \int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta\, \hat{X}^{*}\frac{{\rm d}}{{\rm d}\theta} \frac{\partial {g}}{\partial \boldsymbol{p}} \frac{{\rm d} \hat{X}}{{\rm d}\theta} + \int_{-\theta_{b}}^{\theta_{b}} \hat{X}^{*}\frac{{\rm d}}{{\rm d}\theta} {g} \frac{{\rm d}}{{\rm d}\theta}\frac{\partial \hat{X}}{\partial \boldsymbol{p}} + \int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta\, \frac{\partial {c}}{\partial \boldsymbol{p}} \lvert \hat{X} \rvert^2 + \int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta \, {c} \hat{X}^{*} \frac{\partial \hat{X}}{\partial \boldsymbol{p}}\nonumber\\ = \frac{\partial \hat{\lambda}}{\partial \boldsymbol{p}} \int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta {f} \lvert \hat{X} \rvert^2 + \hat{\lambda} \int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta \frac{\partial {f}}{\partial \boldsymbol{p}} \lvert \hat{X}\rvert^2 + \hat{\lambda} \int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta {f} \hat{X}^{*} \frac{\partial \hat{X}}{\partial \boldsymbol{p}}. \end{gather}$$
$$\begin{gather} \int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta\, \hat{X}^{*}\frac{{\rm d}}{{\rm d}\theta} \frac{\partial {g}}{\partial \boldsymbol{p}} \frac{{\rm d} \hat{X}}{{\rm d}\theta} + \int_{-\theta_{b}}^{\theta_{b}} \hat{X}^{*}\frac{{\rm d}}{{\rm d}\theta} {g} \frac{{\rm d}}{{\rm d}\theta}\frac{\partial \hat{X}}{\partial \boldsymbol{p}} + \int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta\, \frac{\partial {c}}{\partial \boldsymbol{p}} \lvert \hat{X} \rvert^2 + \int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta \, {c} \hat{X}^{*} \frac{\partial \hat{X}}{\partial \boldsymbol{p}}\nonumber\\ = \frac{\partial \hat{\lambda}}{\partial \boldsymbol{p}} \int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta {f} \lvert \hat{X} \rvert^2 + \hat{\lambda} \int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta \frac{\partial {f}}{\partial \boldsymbol{p}} \lvert \hat{X}\rvert^2 + \hat{\lambda} \int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta {f} \hat{X}^{*} \frac{\partial \hat{X}}{\partial \boldsymbol{p}}. \end{gather}$$Using integration by parts, (B1) and rearranging (B3), we can write
 $$\begin{gather} \int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta \left(\dfrac{\partial {c}}{\partial \boldsymbol{p}}\lvert \hat{X}\rvert^2 - \dfrac{\partial g}{\partial \boldsymbol{p}}\left\lvert \dfrac{{\rm d}\hat{X}}{{\rm d}\theta}\right\rvert^2 - \hat{\lambda} \dfrac{\partial {f}}{\partial \boldsymbol{p}} \lvert \hat{X}\rvert^2 \right)- \frac{\partial \hat{\lambda}}{\partial \boldsymbol{p}} \int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta {f} \lvert \hat{X} \rvert^2\nonumber\\ = \int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta \left( -\frac{{\rm d}}{{\rm d}\theta} {g} \frac{{\rm d}\hat{X}^{*}}{{\rm d}\theta} - {c} \hat{X}^{*} + \hat{\lambda} {f} \hat{X}^{*} \right) \frac{\partial \hat{X}}{\partial \boldsymbol{p}}. \end{gather}$$
$$\begin{gather} \int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta \left(\dfrac{\partial {c}}{\partial \boldsymbol{p}}\lvert \hat{X}\rvert^2 - \dfrac{\partial g}{\partial \boldsymbol{p}}\left\lvert \dfrac{{\rm d}\hat{X}}{{\rm d}\theta}\right\rvert^2 - \hat{\lambda} \dfrac{\partial {f}}{\partial \boldsymbol{p}} \lvert \hat{X}\rvert^2 \right)- \frac{\partial \hat{\lambda}}{\partial \boldsymbol{p}} \int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta {f} \lvert \hat{X} \rvert^2\nonumber\\ = \int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta \left( -\frac{{\rm d}}{{\rm d}\theta} {g} \frac{{\rm d}\hat{X}^{*}}{{\rm d}\theta} - {c} \hat{X}^{*} + \hat{\lambda} {f} \hat{X}^{*} \right) \frac{\partial \hat{X}}{\partial \boldsymbol{p}}. \end{gather}$$Due to the self-adjoint property of ideal MHD, the right-hand side of (B4) is zero. The rest of the equation can be arranged so that
 \begin{equation} \frac{\partial \hat{\lambda}}{\partial \boldsymbol{p}} = \frac{\int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta \left(\dfrac{\partial {c}}{\partial \boldsymbol{p}}\lvert \hat{X}\rvert^2 - \dfrac{\partial {g}}{\partial \boldsymbol{p}}\left\lvert \dfrac{{\rm d}\hat{X}}{{\rm d}\theta}\right\rvert^2 - \hat{\lambda} \dfrac{\partial {f}}{\partial \boldsymbol{p}} \lvert \hat{X}\rvert^2 \right)}{\int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta {f}\lvert \hat{X}\rvert^2}. \end{equation}
\begin{equation} \frac{\partial \hat{\lambda}}{\partial \boldsymbol{p}} = \frac{\int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta \left(\dfrac{\partial {c}}{\partial \boldsymbol{p}}\lvert \hat{X}\rvert^2 - \dfrac{\partial {g}}{\partial \boldsymbol{p}}\left\lvert \dfrac{{\rm d}\hat{X}}{{\rm d}\theta}\right\rvert^2 - \hat{\lambda} \dfrac{\partial {f}}{\partial \boldsymbol{p}} \lvert \hat{X}\rvert^2 \right)}{\int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta {f}\lvert \hat{X}\rvert^2}. \end{equation}
Therefore, to calculate ![]() $\partial \hat {\lambda }/\partial \boldsymbol {p}$, we only need the gradients of the geometric coefficients
$\partial \hat {\lambda }/\partial \boldsymbol {p}$, we only need the gradients of the geometric coefficients ![]() ${g}, {c}$,
${g}, {c}$, ![]() ${f}$, the eigenfunction
${f}$, the eigenfunction ![]() $\hat {X}$ and the eigenvalue
$\hat {X}$ and the eigenvalue ![]() $\hat {\lambda }$ of the ballooning equation; we have to solve the ideal ballooning equation only once. This speeds up the optimisation loop, as it is much faster to obtain the gradient of the geometric coefficients than to solve the ballooning equation multiple times.
$\hat {\lambda }$ of the ballooning equation; we have to solve the ideal ballooning equation only once. This speeds up the optimisation loop, as it is much faster to obtain the gradient of the geometric coefficients than to solve the ballooning equation multiple times.
B.1. Extending our adjoint-based technique to equilibrium-dependent DoFs
In this paper, we have used an adjoint method to find the maximum eigenvalue ![]() $\hat {\lambda }_\textrm {max}$ with respect to the parameters
$\hat {\lambda }_\textrm {max}$ with respect to the parameters ![]() $\hat {\boldsymbol {p}}$ of the ballooning equation. It is possible to extend our method to minimise
$\hat {\boldsymbol {p}}$ of the ballooning equation. It is possible to extend our method to minimise ![]() $f_\textrm {ball}$ to the equilibrium parameters
$f_\textrm {ball}$ to the equilibrium parameters ![]() $\tilde {\boldsymbol {p}}$ under the appropriate conditions. We define the problem and find the pertinent conditions in this appendix. We want to find
$\tilde {\boldsymbol {p}}$ under the appropriate conditions. We define the problem and find the pertinent conditions in this appendix. We want to find
where all symbols are defined in § 4 and the ballooning objective function ![]() $f_\textrm {ball}$ is defined in (5.1). To minimise
$f_\textrm {ball}$ is defined in (5.1). To minimise ![]() $f_\textrm {ball}$ with respect to the equilibrium parameters, we need
$f_\textrm {ball}$ with respect to the equilibrium parameters, we need
 \begin{equation} \frac{{\rm d}
f_{\rm{ball}}}{{\rm d} \tilde{\boldsymbol{p}}} =\left.
\frac{\partial f_{\rm{ball}}}{\partial
\hat{\lambda}_{\rm{max}}}\right\lvert_{\tilde{\boldsymbol{p}},
\hat{\boldsymbol{p}}}\frac{\partial
\hat{\lambda}_{\rm{max}}}{\partial
\tilde{\boldsymbol{p}}}+
\left.\frac{\partial f_{\rm{ball}}}{\partial
\hat{\boldsymbol{p}}}\right\lvert_{\hat{\lambda}_{\rm{max}},
\tilde{\boldsymbol{p}}}\frac{\partial
\hat{\boldsymbol{p}}}{\partial
\tilde{\boldsymbol{p}}}
+ \left.\frac{\partial f_{\rm{ball}}}{\partial
\tilde{\boldsymbol{p}}}\right\lvert_{\hat{\lambda}_{\rm{max}},
\hat{\boldsymbol{p}}}.
\end{equation}
\begin{equation} \frac{{\rm d}
f_{\rm{ball}}}{{\rm d} \tilde{\boldsymbol{p}}} =\left.
\frac{\partial f_{\rm{ball}}}{\partial
\hat{\lambda}_{\rm{max}}}\right\lvert_{\tilde{\boldsymbol{p}},
\hat{\boldsymbol{p}}}\frac{\partial
\hat{\lambda}_{\rm{max}}}{\partial
\tilde{\boldsymbol{p}}}+
\left.\frac{\partial f_{\rm{ball}}}{\partial
\hat{\boldsymbol{p}}}\right\lvert_{\hat{\lambda}_{\rm{max}},
\tilde{\boldsymbol{p}}}\frac{\partial
\hat{\boldsymbol{p}}}{\partial
\tilde{\boldsymbol{p}}}
+ \left.\frac{\partial f_{\rm{ball}}}{\partial
\tilde{\boldsymbol{p}}}\right\lvert_{\hat{\lambda}_{\rm{max}},
\hat{\boldsymbol{p}}}.
\end{equation}
The most expensive term to calculate in (B7) is the gradient of the eigenvalue ![]() $\lambda$. To obtain that, we take the derivative of the operator
$\lambda$. To obtain that, we take the derivative of the operator ![]() $\mathcal {G}$ with respect to
$\mathcal {G}$ with respect to ![]() $\lambda$,
$\lambda$,
We also express ![]() $\hat {\lambda }$ around a point
$\hat {\lambda }$ around a point ![]() $\boldsymbol {p}_0 = (\tilde {\boldsymbol {p}}_0, \hat {\boldsymbol {p}}_0)$ in the state space as a Taylor series,
$\boldsymbol {p}_0 = (\tilde {\boldsymbol {p}}_0, \hat {\boldsymbol {p}}_0)$ in the state space as a Taylor series,
and assume that the optimiser takes a step size ![]() $|\delta \boldsymbol {p}|$ that is smaller than the radius of convergence of Taylor series (B9),
$|\delta \boldsymbol {p}|$ that is smaller than the radius of convergence of Taylor series (B9),
 \begin{equation} \left\lvert\frac{\partial}{{\partial \tilde{\boldsymbol{p}}} }\frac{\partial \hat{\lambda}}{\partial \tilde{\boldsymbol{p}}} \boldsymbol{:} \delta \tilde{\boldsymbol{p}} \delta \tilde{\boldsymbol{p}} \right\rvert \ll \left\lvert \frac{\partial \hat{\lambda}}{\partial \tilde{\boldsymbol{p}}} \boldsymbol{\cdot} \delta \tilde{\boldsymbol{p}} \right\rvert,\quad \left \lvert\frac{\partial}{{\partial \hat{\boldsymbol{p}}} }\frac{\partial \hat{\lambda}}{\partial \hat{\boldsymbol{p}}} \boldsymbol{:} \delta \hat{\boldsymbol{p}} \delta \hat{\boldsymbol{p}} \right\rvert \ll \left\lvert \frac{\partial \hat{\lambda}}{\partial \hat{\boldsymbol{p}}} \boldsymbol{\cdot} \delta \hat{\boldsymbol{p}} \right\rvert. \end{equation}
\begin{equation} \left\lvert\frac{\partial}{{\partial \tilde{\boldsymbol{p}}} }\frac{\partial \hat{\lambda}}{\partial \tilde{\boldsymbol{p}}} \boldsymbol{:} \delta \tilde{\boldsymbol{p}} \delta \tilde{\boldsymbol{p}} \right\rvert \ll \left\lvert \frac{\partial \hat{\lambda}}{\partial \tilde{\boldsymbol{p}}} \boldsymbol{\cdot} \delta \tilde{\boldsymbol{p}} \right\rvert,\quad \left \lvert\frac{\partial}{{\partial \hat{\boldsymbol{p}}} }\frac{\partial \hat{\lambda}}{\partial \hat{\boldsymbol{p}}} \boldsymbol{:} \delta \hat{\boldsymbol{p}} \delta \hat{\boldsymbol{p}} \right\rvert \ll \left\lvert \frac{\partial \hat{\lambda}}{\partial \hat{\boldsymbol{p}}} \boldsymbol{\cdot} \delta \hat{\boldsymbol{p}} \right\rvert. \end{equation}
Next, we use the fact that ![]() $\partial \hat {\lambda }/\partial \hat {\boldsymbol {p}} = 0$ at
$\partial \hat {\lambda }/\partial \hat {\boldsymbol {p}} = 0$ at ![]() $\hat {\lambda } = \hat {\lambda }_{\mathrm {max}}$, and that our choice of
$\hat {\lambda } = \hat {\lambda }_{\mathrm {max}}$, and that our choice of ![]() $f_\textrm {ball}$ only explicitly depends on
$f_\textrm {ball}$ only explicitly depends on ![]() $\hat {\lambda }_\textrm {max}$. Using the explicit form of the linear operator from (3.1), we multiply (B8) by
$\hat {\lambda }_\textrm {max}$. Using the explicit form of the linear operator from (3.1), we multiply (B8) by ![]() $X^{*}$ and integrate throughout the domain, to rewrite (B7) as
$X^{*}$ and integrate throughout the domain, to rewrite (B7) as
 \begin{equation} \frac{{\rm d} f_{\rm{ball}}}{{\rm d}\boldsymbol{p}} = \sum_{j=1}^{\rm{ns}} \mathrm{ReLU}^{\prime}(\hat{\lambda}_{\mathrm{max},j})\frac{\int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta \left(\dfrac{\partial {c}}{\partial \boldsymbol{p}} \lvert \hat{X}\rvert^2 - \dfrac{\partial g}{\partial \boldsymbol{p}} \left\lvert \dfrac{{\rm d}\hat{X}}{{\rm d}\theta}\right\rvert^2 - \hat{\lambda} \dfrac{\partial {f}}{\partial \boldsymbol{p}} \lvert \hat{X}\rvert^2 \right)}{\int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta\, {f}\lvert \hat{X}\rvert^2}, \end{equation}
\begin{equation} \frac{{\rm d} f_{\rm{ball}}}{{\rm d}\boldsymbol{p}} = \sum_{j=1}^{\rm{ns}} \mathrm{ReLU}^{\prime}(\hat{\lambda}_{\mathrm{max},j})\frac{\int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta \left(\dfrac{\partial {c}}{\partial \boldsymbol{p}} \lvert \hat{X}\rvert^2 - \dfrac{\partial g}{\partial \boldsymbol{p}} \left\lvert \dfrac{{\rm d}\hat{X}}{{\rm d}\theta}\right\rvert^2 - \hat{\lambda} \dfrac{\partial {f}}{\partial \boldsymbol{p}} \lvert \hat{X}\rvert^2 \right)}{\int_{-\theta_{b}}^{\theta_{b}} \,{\rm d}\theta\, {f}\lvert \hat{X}\rvert^2}, \end{equation}
where ![]() $\boldsymbol {p} = (\tilde {\boldsymbol {p}}, \hat {\boldsymbol {p}})$ is the union of all the parameters of the problem and
$\boldsymbol {p} = (\tilde {\boldsymbol {p}}, \hat {\boldsymbol {p}})$ is the union of all the parameters of the problem and ![]() $\mathrm {ReLU}^{\prime }$Footnote 7 is the derivative of the
$\mathrm {ReLU}^{\prime }$Footnote 7 is the derivative of the ![]() $\mathrm {ReLU}$ operator such that
$\mathrm {ReLU}$ operator such that
 \begin{equation} \mathrm{ReLU}^{\prime}(x)= \begin{cases} 0, & \text{if } x < 0,\\ 1, & x> 0. \end{cases} \end{equation}
\begin{equation} \mathrm{ReLU}^{\prime}(x)= \begin{cases} 0, & \text{if } x < 0,\\ 1, & x> 0. \end{cases} \end{equation}
Calculating the derivative of the geometric coefficients ![]() ${g}$,
${g}$, ![]() ${c}$ and
${c}$ and ![]() ${f}$ with respect to the equilibrium parameter vector
${f}$ with respect to the equilibrium parameter vector ![]() $\tilde {\boldsymbol {p}}$ is not straightforward in VMEC and may lack the requisite accuracy for an adjoint method to work. However, an equilibrium solver such as DESC (Dudt & Kolemen Reference Dudt and Kolemen2020; Conlin et al. Reference Conlin, Dudt, Panici and Kolemen2022; Panici et al. Reference Panici, Conlin, Dudt and Kolemen2022) that is designed to calculate these gradients along with the geometric coefficients accurately may enable us to utilise the full potential of this adjoint-based method. Since the speed up obtained with an adjoint method is linearly proportional to the length of the vector
$\tilde {\boldsymbol {p}}$ is not straightforward in VMEC and may lack the requisite accuracy for an adjoint method to work. However, an equilibrium solver such as DESC (Dudt & Kolemen Reference Dudt and Kolemen2020; Conlin et al. Reference Conlin, Dudt, Panici and Kolemen2022; Panici et al. Reference Panici, Conlin, Dudt and Kolemen2022) that is designed to calculate these gradients along with the geometric coefficients accurately may enable us to utilise the full potential of this adjoint-based method. Since the speed up obtained with an adjoint method is linearly proportional to the length of the vector ![]() $\tilde {\boldsymbol {p}}$, using (B12) we can, in principle, speed up the calculation of
$\tilde {\boldsymbol {p}}$, using (B12) we can, in principle, speed up the calculation of ![]() $d f_\textrm {ball}/\textrm {d}\tilde {\boldsymbol {p}}$ by an order of magnitude for 2D axisymmetric equilibria and by two orders or magnitude for 3D equilibria.
$d f_\textrm {ball}/\textrm {d}\tilde {\boldsymbol {p}}$ by an order of magnitude for 2D axisymmetric equilibria and by two orders or magnitude for 3D equilibria.
B.2. Extending our adjoint technique to low- $n$, ideal MHD solvers
$n$, ideal MHD solvers
Note that this process can be applied to any ideal MHD eigenvalue solver. For fluctuations that are not confined to a flux surface, one can solve for a fluctuation of the form
where ![]() $X = \{X_{\psi }, X_{\alpha }\}$ are components of fluctuation
$X = \{X_{\psi }, X_{\alpha }\}$ are components of fluctuation ![]() $X$ perpendicular to the equilibrium magnetic field line, and
$X$ perpendicular to the equilibrium magnetic field line, and ![]() $m$ and
$m$ and ![]() $n$ are the poloidal and toroidal mode numbers, respectively. We solve for
$n$ are the poloidal and toroidal mode numbers, respectively. We solve for ![]() $\hat {X}(\psi )$, using codes such as
$\hat {X}(\psi )$, using codes such as ![]() $\texttt {ELITE}$ and
$\texttt {ELITE}$ and ![]() $\texttt {GATO}$ (Bernard, Helton & Moore Reference Bernard, Helton and Moore1981) for axisymmetric equilibria or
$\texttt {GATO}$ (Bernard, Helton & Moore Reference Bernard, Helton and Moore1981) for axisymmetric equilibria or ![]() $\texttt {TERPSICHORE}$ (Anderson et al. Reference Anderson, Cooper, Gruber, Merazzi and Schwenn1990),
$\texttt {TERPSICHORE}$ (Anderson et al. Reference Anderson, Cooper, Gruber, Merazzi and Schwenn1990), ![]() $\texttt {CAS-3D}$ (Schwab Reference Schwab1993) for 3D equilibria. For
$\texttt {CAS-3D}$ (Schwab Reference Schwab1993) for 3D equilibria. For ![]() $\texttt {GATO}$,
$\texttt {GATO}$, ![]() $\texttt {TERPSICHORE}$, and
$\texttt {TERPSICHORE}$, and ![]() $\texttt {CAS-3D}$, the ideal MHD energy principle is used to solve the matrix equation
$\texttt {CAS-3D}$, the ideal MHD energy principle is used to solve the matrix equation
where ![]() $\mathcal {A}$ and
$\mathcal {A}$ and ![]() $\mathcal {B}$ are real symmetric matrices. Currently, solving such an equation using these codes takes at least a few minutes. For such a problem, we can repeat the process explained at the beginning of this appendix to obtain the gradient,
$\mathcal {B}$ are real symmetric matrices. Currently, solving such an equation using these codes takes at least a few minutes. For such a problem, we can repeat the process explained at the beginning of this appendix to obtain the gradient,
for all modes. Equation (B16) is similar to the Hellman–Feynman theorem (Hellmann Reference Hellmann1933; Feynman Reference Feynman1939). For axisymmetric equilibria, combining gradient information with fast equilibrium solvers such as ![]() $\texttt {EFIT}$ (Lao et al. Reference Lao, John, Stambaugh, Kellman and Pfeiffer1985) can help mitigate real-time disruption. One could also couple this adjoint approach with an optimiser to find low-
$\texttt {EFIT}$ (Lao et al. Reference Lao, John, Stambaugh, Kellman and Pfeiffer1985) can help mitigate real-time disruption. One could also couple this adjoint approach with an optimiser to find low-![]() $n$, ideal MHD stable equilibria.
$n$, ideal MHD stable equilibria.