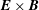1 Introduction
Sheared flows in plasmas are ubiquitous and their effect on plasma instabilities and turbulence can be one of either suppression or enhancement. Sheared flows are often stabilizing when the local shearing rate is comparable to the linear growth rate of an unstable mode, and can nonlinearly suppress turbulence and transport by decorrelation of turbulent eddies (Burrell Reference Burrell1997; Terry Reference Terry2000). In this paper, we focus on a competing effect: sheared flows also provide a source of free energy for instabilities such as the Kelvin–Helmholtz (KH) mode.
The study of velocity shear instabilities in plasmas has a long history dating back many decades, going up to the present, and encompassing both space and fusion applications. The cited papers which follow are but a few examples of the rich literature on this topic. Magnetized plasmas generally have anisotropic flows across
![]() $(\boldsymbol{v}_{\bot })$
and along
$(\boldsymbol{v}_{\bot })$
and along
![]() $(\boldsymbol{v}_{\Vert })$
the magnetic field, and these flows can have both perpendicular
$(\boldsymbol{v}_{\Vert })$
the magnetic field, and these flows can have both perpendicular
![]() $(\boldsymbol{{\rm\nabla}}_{\bot })$
and parallel
$(\boldsymbol{{\rm\nabla}}_{\bot })$
and parallel
![]() $(\boldsymbol{{\rm\nabla}}_{\Vert })$
gradients. The resulting instabilities broadly separate into classes depending on whether the free energy source is from the parallel velocity shear
$(\boldsymbol{{\rm\nabla}}_{\Vert })$
gradients. The resulting instabilities broadly separate into classes depending on whether the free energy source is from the parallel velocity shear
![]() $\boldsymbol{{\rm\nabla}}_{\bot }\boldsymbol{v}_{\Vert }$
(D’Angelo Reference D’Angelo1965; Catto, Rosenbluth & Liu Reference Catto, Rosenbluth and Liu1973; Garbet et al.
Reference Garbet, Fenzi, Capes, Devynck and Antar1999; Wang et al.
Reference Wang, Ethier, Ren, Kaye, Chen, Startsev, Lu and Li2015), the parallel shear of the perpendicular flows
$\boldsymbol{{\rm\nabla}}_{\bot }\boldsymbol{v}_{\Vert }$
(D’Angelo Reference D’Angelo1965; Catto, Rosenbluth & Liu Reference Catto, Rosenbluth and Liu1973; Garbet et al.
Reference Garbet, Fenzi, Capes, Devynck and Antar1999; Wang et al.
Reference Wang, Ethier, Ren, Kaye, Chen, Startsev, Lu and Li2015), the parallel shear of the perpendicular flows
![]() $\boldsymbol{{\rm\nabla}}_{\Vert }\boldsymbol{v}_{\bot }$
(Lee, Catto & Aamodt Reference Lee, Catto and Aamodt1982; Tsidulko, Berk & Cohen Reference Tsidulko, Berk and Cohen1994) or the perpendicular ‘transverse’ shear of the perpendicular flows
$\boldsymbol{{\rm\nabla}}_{\Vert }\boldsymbol{v}_{\bot }$
(Lee, Catto & Aamodt Reference Lee, Catto and Aamodt1982; Tsidulko, Berk & Cohen Reference Tsidulko, Berk and Cohen1994) or the perpendicular ‘transverse’ shear of the perpendicular flows
![]() $\boldsymbol{b}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\bot }\times \boldsymbol{v}_{\bot }$
(Perkins & Jassby Reference Perkins and Jassby1971; Miura & Pritchett Reference Miura and Pritchett1982; Horton, Tajima & Kamimura Reference Horton, Tajima and Kamimura1987; Pritchett Reference Pritchett1987; Vranješ & Tanaka Reference Vranješ and Tanaka2002; Rogers & Dorland Reference Rogers and Dorland2005; Popovich et al.
Reference Popovich, Umansky, Carter and Friedman2010; Xi et al.
Reference Xi, Xu, Wang and Xia2012; Fisher et al.
Reference Fisher, Rogers, Rossi and Guice2015). In the present paper we will be concerned only with the latter, and by KH we will mean the transverse KH instability. In tokamak plasmas, also the primary concern of this paper, this typically means the KH mode that is driven by the shear
$\boldsymbol{b}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{\bot }\times \boldsymbol{v}_{\bot }$
(Perkins & Jassby Reference Perkins and Jassby1971; Miura & Pritchett Reference Miura and Pritchett1982; Horton, Tajima & Kamimura Reference Horton, Tajima and Kamimura1987; Pritchett Reference Pritchett1987; Vranješ & Tanaka Reference Vranješ and Tanaka2002; Rogers & Dorland Reference Rogers and Dorland2005; Popovich et al.
Reference Popovich, Umansky, Carter and Friedman2010; Xi et al.
Reference Xi, Xu, Wang and Xia2012; Fisher et al.
Reference Fisher, Rogers, Rossi and Guice2015). In the present paper we will be concerned only with the latter, and by KH we will mean the transverse KH instability. In tokamak plasmas, also the primary concern of this paper, this typically means the KH mode that is driven by the shear
![]() $\text{d}v_{y}/\text{d}x$
where (
$\text{d}v_{y}/\text{d}x$
where (
![]() $x,y,z$
) describe approximately the radial, binormal (in tokamak terminology approximately poloidal) and parallel directions to the magnetic field. In the material which follows we will consider KH instability models in both this simple slab geometry and in fully toroidal divertor geometry relevant to tokamak edge and scrape-off layer plasmas.
$x,y,z$
) describe approximately the radial, binormal (in tokamak terminology approximately poloidal) and parallel directions to the magnetic field. In the material which follows we will consider KH instability models in both this simple slab geometry and in fully toroidal divertor geometry relevant to tokamak edge and scrape-off layer plasmas.
One motivation for studying the KH mode is its possible role in determining saturation levels for other unstable modes (Itoh et al.
Reference Itoh, Itoh, Diamond, Hahm, Fujisawa, Tynan, Yagi and Nagashima2006; Ricci & Rogers Reference Ricci and Rogers2013; Goto et al.
Reference Goto, Miura, Ito, Sato and Hatori2015). Reynolds stress arising from a primary instability, e.g. a curvature-driven resistive ballooning mode as in Guzdar et al. (Reference Guzdar, Drake, McCarthy, Hassam and Liu1993), and references therein, acts as a source for both zonal (oscillating) and mean (time averaged) flows. When shear in the resulting flows becomes sufficiently large,
![]() $\text{d}v_{y}/\text{d}x\sim {\it\gamma}$
, i.e. comparable to the primary instability growth rate
$\text{d}v_{y}/\text{d}x\sim {\it\gamma}$
, i.e. comparable to the primary instability growth rate
![]() ${\it\gamma}$
, nonlinear saturation may occur. On the other hand, if the resulting sheared flows are mitigated or destroyed by secondary KH instability, the primary mode may continue to grow. Understanding the conditions for KH instability is thus important for determining the amplitude scaling of saturated turbulence.
${\it\gamma}$
, nonlinear saturation may occur. On the other hand, if the resulting sheared flows are mitigated or destroyed by secondary KH instability, the primary mode may continue to grow. Understanding the conditions for KH instability is thus important for determining the amplitude scaling of saturated turbulence.
An application of particular present day interest for fusion research is the resulting scaling of the scrape-off layer (SOL) heat flux width implied by turbulent cross-field transport (Myra, D’Ippolito & Russell Reference Myra, D’Ippolito and Russell2015). (The SOL is the region of open field lines just outside the confined plasma. In a tokamak, the heat from the confined core plasma transports across the separatrix or last closed flux surface, into the SOL where it is ultimately deposited on material surfaces.) It is worth noting that edge- and near-SOL plasmas can have very short perpendicular gradient scale lengths, of the order of a few mm to a few cm, in both the plasma pressure profiles and the drift velocities, making for potentially strong instability driving terms.
In spite of the considerable literature on the transverse KH instability in magnetized plasmas, reviewed briefly in the following paragraphs, significant questions remain to be addressed clearly even in the linear theory. Because the KH instability cannot be obtained from a local dispersion relation, it is usually treated numerically, and this has hampered the development of simple criteria for stability boundaries, particularly when density gradients, ion diamagnetic effects and parallel currents are present simultaneously. Finally, to the best of our knowledge, there has been no attempt to date to examine the KH instability near the separatrix and in the SOL in a realistic toroidal geometry. Both of these topics are addressed in the present paper.
Although the KH mode does not obey a local dispersion relation, various models employing specialized velocity profiles have been employed to obtain analytical or semi-analytical results, including ‘sharp boundary’ (discontinuous) (Pritchett Reference Pritchett1987), piecewise linear (Horton et al. Reference Horton, Tajima and Kamimura1987) and tanh-type (Vranješ & Tanaka Reference Vranješ and Tanaka2002) velocity profiles. While many of the early papers considered the basic KH instability with velocity gradients in an otherwise minimal plasma model, later works also included the stabilizing effect of Alfvén parallel currents, i.e. magnetic line bending energy (Miura & Pritchett Reference Miura and Pritchett1982; Rogers & Dorland Reference Rogers and Dorland2005) and ion diamagnetic drifts (Vranješ & Tanaka Reference Vranješ and Tanaka2002; Rogers & Dorland Reference Rogers and Dorland2005). Although some of the literature relevant to inertial confinement fusion considers KH instability in the presence of a density gradient (Wang et al. Reference Wang, Xue, Ye and Li2009), the simultaneous treatment of parallel currents, velocity, density and ion pressure gradients necessary to understand magnetic-fusion-relevant plasmas has, to the best of our knowledge, only been attempted in numerical studies (Goto et al. Reference Goto, Miura, Ito, Sato and Hatori2015).
The key known results from previous work can be summarized as follows. The basic KH mode is unstable over a range of perpendicular wavenumbers
![]() $k_{y}$
directed along the flow
$k_{y}$
directed along the flow
![]() $v_{y}$
, extending from
$v_{y}$
, extending from
![]() $k_{y}=0$
to a maximum cutoff wavenumber
$k_{y}=0$
to a maximum cutoff wavenumber
![]() $k_{max}\sim 1/L_{v}$
where
$k_{max}\sim 1/L_{v}$
where
![]() $L_{v}$
is the scale length of the velocity profile,
$L_{v}$
is the scale length of the velocity profile,
![]() $L_{v}^{-1}\sim \text{d}\ln (v_{y})/\text{d}x$
. The KH growth rate is maximized at
$L_{v}^{-1}\sim \text{d}\ln (v_{y})/\text{d}x$
. The KH growth rate is maximized at
![]() $k_{y}L_{v}\sim 0.5$
and the maximum growth rate is of order
$k_{y}L_{v}\sim 0.5$
and the maximum growth rate is of order
![]() ${\it\gamma}_{max}\sim 0.2v_{y,max}^{\prime }$
where
${\it\gamma}_{max}\sim 0.2v_{y,max}^{\prime }$
where
![]() $v_{y,max}^{\prime }$
is the maximum shearing rate of the profile and here
$v_{y,max}^{\prime }$
is the maximum shearing rate of the profile and here
![]() $^{\prime }$
denotes
$^{\prime }$
denotes
![]() $\text{d}/\text{d}x$
. The function
$\text{d}/\text{d}x$
. The function
![]() ${\it\gamma}(k_{y})$
has a characteristic inverted-parabola shape as illustrated in figure 1. In the limit
${\it\gamma}(k_{y})$
has a characteristic inverted-parabola shape as illustrated in figure 1. In the limit
![]() $k_{y}L_{v}\ll 1$
, the growth rate scales like
$k_{y}L_{v}\ll 1$
, the growth rate scales like
![]() ${\it\gamma}\sim Ck_{y}L_{v}{\it\gamma}_{max}$
where
${\it\gamma}\sim Ck_{y}L_{v}{\it\gamma}_{max}$
where
![]() $C$
is an order unity constant.
$C$
is an order unity constant.

Figure 1. Computed growth rate (solid) and real part of the frequency (dashed) for the KH mode using a diffuse radial profile model (Popovich et al. Reference Popovich, Umansky, Carter and Friedman2010) and sample parameters from the LAPD experiment. Figure reproduced from Phys. Plasmas 17, 102107,1-11 (2010).
The Alfvén parallel current stabilizes the KH mode when, in order of magnitude,
![]() ${\it\omega}_{a}>{\it\gamma}_{max}$
where
${\it\omega}_{a}>{\it\gamma}_{max}$
where
![]() ${\it\omega}_{a}=k_{\Vert }v_{a}$
. Here,
${\it\omega}_{a}=k_{\Vert }v_{a}$
. Here,
![]() $k_{\Vert }$
is the parallel wavenumber and
$k_{\Vert }$
is the parallel wavenumber and
![]() $v_{a}=B/(4{\rm\pi}nm_{i})^{1/2}$
is the Alfvén velocity. Tokamak plasmas have magnetic shear (i.e. variation, from one flux surface to the next of the pitch angle of the magnetic field with respect to the toroidal direction). Magnetic shear imposes a minimum effective
$v_{a}=B/(4{\rm\pi}nm_{i})^{1/2}$
is the Alfvén velocity. Tokamak plasmas have magnetic shear (i.e. variation, from one flux surface to the next of the pitch angle of the magnetic field with respect to the toroidal direction). Magnetic shear imposes a minimum effective
![]() $k_{\Vert }$
on the perturbation: the fixed twist of the mode and the shear of the magnetic field prevent the mode from staying aligned from one flux surface to the next. Thus KH stability can also be brought about by magnetic shear effects.
$k_{\Vert }$
on the perturbation: the fixed twist of the mode and the shear of the magnetic field prevent the mode from staying aligned from one flux surface to the next. Thus KH stability can also be brought about by magnetic shear effects.
Ion diamagnetic flows
![]() $v_{di}\sim v_{ti}{\it\rho}_{i}/L_{pi}$
become important when
$v_{di}\sim v_{ti}{\it\rho}_{i}/L_{pi}$
become important when
![]() $v_{di}\sim v_{E}$
where the KH instability is driven by the gradient in the
$v_{di}\sim v_{E}$
where the KH instability is driven by the gradient in the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
velocity
$\boldsymbol{E}\times \boldsymbol{B}$
velocity
![]() $\boldsymbol{v}_{E}=\boldsymbol{E}\times \boldsymbol{B}c/B^{2}$
and
$\boldsymbol{v}_{E}=\boldsymbol{E}\times \boldsymbol{B}c/B^{2}$
and
![]() $\boldsymbol{E}$
and
$\boldsymbol{E}$
and
![]() $\boldsymbol{B}$
are the equilibrium electric and magnetic fields. Here
$\boldsymbol{B}$
are the equilibrium electric and magnetic fields. Here
![]() $v_{ti}$
is the ion thermal velocity,
$v_{ti}$
is the ion thermal velocity,
![]() ${\it\rho}_{i}$
is the ion Larmor radius,
${\it\rho}_{i}$
is the ion Larmor radius,
![]() $L_{pi}$
is the gradient scale length of the ion pressure and the relevant components of
$L_{pi}$
is the gradient scale length of the ion pressure and the relevant components of
![]() $v_{di}$
and
$v_{di}$
and
![]() $v_{E}$
are in the
$v_{E}$
are in the
![]() $y$
direction. More precisely, since
$y$
direction. More precisely, since
![]() $v_{E}$
is frame dependent, the condition is
$v_{E}$
is frame dependent, the condition is
![]() $v_{di}\sim {\rm\Delta}v_{E}$
where
$v_{di}\sim {\rm\Delta}v_{E}$
where
![]() ${\rm\Delta}v_{E}$
is the net change in
${\rm\Delta}v_{E}$
is the net change in
![]() $v_{E}(x)$
across a characteristic distance in
$v_{E}(x)$
across a characteristic distance in
![]() $x$
of order
$x$
of order
![]() $L_{v}$
. Density gradients usually reduce the growth rate of the KH mode, but cannot completely stabilize it.
$L_{v}$
. Density gradients usually reduce the growth rate of the KH mode, but cannot completely stabilize it.
The plan of our paper is as follows. In § 2 a simple analytical model of the KH mode is presented in the asymptotic limit
![]() $k_{y}L_{v}\ll 1$
, which is equivalent to a sharp boundary model. The analytic model treats sheared
$k_{y}L_{v}\ll 1$
, which is equivalent to a sharp boundary model. The analytic model treats sheared
![]() $\boldsymbol{E}\times \boldsymbol{B}$
flows, ion diamagnetism, density gradients and parallel currents in a slab geometry, enabling a unified summary that encompasses and extends well-known results. The model employs a warm ion treatment including ion gyro-viscous terms that are consistent with the drift ordered, fluid model result derived by Simakov & Catto (Reference Simakov and Catto2003) and used in the BOUT (Umansky et al.
Reference Umansky, Xu, Dudson, LoDestro and Myra2009) and SOLT (Russell et al.
Reference Russell, D’Ippolito, Myra, Canik, Gray and Zweben2015) codes. These somewhat complicated additional terms are the same order as the usual ion diamagnetic drift term and influence the KH stability boundary. To the best of our knowledge, they have not previously been treated in any analytical KH model and are also omitted in some numerical studies. Remarkably, a simple, analytical dispersion relation is still possible in the
$\boldsymbol{E}\times \boldsymbol{B}$
flows, ion diamagnetism, density gradients and parallel currents in a slab geometry, enabling a unified summary that encompasses and extends well-known results. The model employs a warm ion treatment including ion gyro-viscous terms that are consistent with the drift ordered, fluid model result derived by Simakov & Catto (Reference Simakov and Catto2003) and used in the BOUT (Umansky et al.
Reference Umansky, Xu, Dudson, LoDestro and Myra2009) and SOLT (Russell et al.
Reference Russell, D’Ippolito, Myra, Canik, Gray and Zweben2015) codes. These somewhat complicated additional terms are the same order as the usual ion diamagnetic drift term and influence the KH stability boundary. To the best of our knowledge, they have not previously been treated in any analytical KH model and are also omitted in some numerical studies. Remarkably, a simple, analytical dispersion relation is still possible in the
![]() $k_{y}L_{v}\ll 1$
limit.
$k_{y}L_{v}\ll 1$
limit.
Having addressed the effects of ion diamagnetism, density gradients, parallel currents and their mutual interactions in a simple geometry, in § 3 the effect of realistic toroidal geometry is explored numerically using the 2DX eigenvalue code (Baver, Myra & Umansky Reference Baver, Myra and Umansky2011) for KH modes both inside and outside the separatrix. For this portion of the study, a minimal cold ion KH model is employed. An invariant scaling analysis is shown to reduce the parameter space and isolate the main dependencies on wavenumber, Alfvén parallel current, electron skin depth and collisionality. It is shown for a sample spherical torus magnetic geometry that the KH mode is more unstable in the near separatrix and SOL than in the closed surface region.
In § 4 a method for qualitatively including the stabilizing effect of parallel Alfvén currents on the KH mode in 2-D reduced model nonlinear simulations is presented. Finally our conclusions are given in § 5.
As mentioned in the preceding, various limitations apply separately to the different sections of the paper: the use of slab geometry in § 2 and the use of a cold ion model in §§ 3 and 4. The goal of this approach is to highlight individual effects in an attempt to gain insight, rather than to include all important effects simultaneously. The latter approach would be required, for example, for quantitative modelling of an experimental discharge.
2 Analytical model of KH mode
In this section an analytical theory of the KH mode including warm ion effects is considered in a slab geometry. The slab geometry is a significant limitation for tokamak applications because of magnetic shear, discussed in § 3, and the implications of coupling of perpendicular and parallel flows in a toroidal geometry. Nevertheless, the slab model, being analytically tractable, provides some useful insights.
2.1 Radial eigenvalue equation
The basic equations of the warm ion fluid model considered in this section are given by charge conservation (vorticity), and advection for the density and ion pressure.
Here and in the following we employ Bohm-normalized variables, i.e. length and time scales are normalized to
![]() ${\it\rho}_{s}=c_{s}/{\it\Omega}_{i}$
and
${\it\rho}_{s}=c_{s}/{\it\Omega}_{i}$
and
![]() $1/{\it\Omega}_{i}$
, respectively, the electrostatic potential is normalized to
$1/{\it\Omega}_{i}$
, respectively, the electrostatic potential is normalized to
![]() $e/T_{e0}$
and the density and temperature are normalized to arbitrary values
$e/T_{e0}$
and the density and temperature are normalized to arbitrary values
![]() $n_{0}$
and
$n_{0}$
and
![]() $T_{e0}$
. The generalized plasma vorticity (including finite ion pressure effects) is given by
$T_{e0}$
. The generalized plasma vorticity (including finite ion pressure effects) is given by
![]() $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{f}$
and in (2.1) the last term on the left-hand side employs Cartesian tensor notation with implicit sums on repeated indices and
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{f}$
and in (2.1) the last term on the left-hand side employs Cartesian tensor notation with implicit sums on repeated indices and
![]() $i,j$
taking the values
$i,j$
taking the values
![]() $x,y$
, i.e. the coordinates perpendicular to the magnetic field
$x,y$
, i.e. the coordinates perpendicular to the magnetic field
![]() $\boldsymbol{B}=\boldsymbol{b}B$
. It is shown in appendix A that (2.1) is equivalent to the fluid vorticity equation used in the BOUT and SOLT codes which are consistent with the (Simakov & Catto Reference Simakov and Catto2003) result for the gyro-viscous terms.
$\boldsymbol{B}=\boldsymbol{b}B$
. It is shown in appendix A that (2.1) is equivalent to the fluid vorticity equation used in the BOUT and SOLT codes which are consistent with the (Simakov & Catto Reference Simakov and Catto2003) result for the gyro-viscous terms.
The linearization of (2.1)–(2.4) with modes proportional to
![]() $\exp (\text{i}k_{y}y-\text{i}{\it\omega}t)$
yields
$\exp (\text{i}k_{y}y-\text{i}{\it\omega}t)$
yields
We have assumed a slab equilibrium where
![]() $n$
,
$n$
,
![]() $p_{i}$
,
$p_{i}$
,
![]() ${\it\Phi}$
and hence
${\it\Phi}$
and hence
![]() $v_{y}$
are functions of
$v_{y}$
are functions of
![]() $x$
alone. As a result
$x$
alone. As a result
![]() $\boldsymbol{v}=\boldsymbol{e}_{y}v_{y}$
and
$\boldsymbol{v}=\boldsymbol{e}_{y}v_{y}$
and
![]() $\boldsymbol{f}=\boldsymbol{e}_{x}f_{x}$
with
$\boldsymbol{f}=\boldsymbol{e}_{x}f_{x}$
with
![]() $v_{y}=\partial _{x}{\it\Phi}={\it\Phi}^{\prime }$
and
$v_{y}=\partial _{x}{\it\Phi}={\it\Phi}^{\prime }$
and
![]() $f_{x}=nv_{y}+p_{i}^{\prime }$
. After a small manipulation the vorticity equation takes the form
$f_{x}=nv_{y}+p_{i}^{\prime }$
. After a small manipulation the vorticity equation takes the form
We can write
![]() $-k_{y}v_{y}^{\prime }=\partial _{x}\tilde{{\it\omega}}$
which allows combining of the corresponding term with the
$-k_{y}v_{y}^{\prime }=\partial _{x}\tilde{{\it\omega}}$
which allows combining of the corresponding term with the
![]() $\tilde{{\it\omega}}$
term as follows
$\tilde{{\it\omega}}$
term as follows
On substitution for
![]() ${\it\delta}n$
and
${\it\delta}n$
and
![]() ${\it\delta}p_{i}$
the preceding equation becomes an explicit second-order radial eigenvalue equation describing the KH mode in the presence of density and ion pressure profiles. The driving term is the gradient in the equilibrium vorticity,
${\it\delta}p_{i}$
the preceding equation becomes an explicit second-order radial eigenvalue equation describing the KH mode in the presence of density and ion pressure profiles. The driving term is the gradient in the equilibrium vorticity,
![]() $f_{x}^{\prime \prime }$
contained in the second to last term. It is remarkable that, after some straightforward but tedious algebraic manipulations, this radial eigenvalue equation takes a rather simple form:
$f_{x}^{\prime \prime }$
contained in the second to last term. It is remarkable that, after some straightforward but tedious algebraic manipulations, this radial eigenvalue equation takes a rather simple form:
where
It is worth noting that the simple (and as we shall see, integrable) form expressed by (2.11) is only made possible by the inclusion of the gyro-viscous terms contained in
![]() $(\partial _{j}v_{i})(\partial _{i}\,f_{j})$
.
$(\partial _{j}v_{i})(\partial _{i}\,f_{j})$
.
2.2 Sharp boundary model
To make further analytical progress, we specialize to the sharp boundary model where profiles of
![]() $v_{y}(x)$
,
$v_{y}(x)$
,
![]() $n(x)$
, and
$n(x)$
, and
![]() $p_{i}^{\prime }(x)$
(hence
$p_{i}^{\prime }(x)$
(hence
![]() $f_{x}$
and
$f_{x}$
and
![]() $A$
) are flat in the ‘left’ and ‘right’ regions labelled ‘1’ and ‘2’, respectively, and take a discontinuous jump at the junction between these regions. The sharp boundary limit gives solutions in the asymptotic limit
$A$
) are flat in the ‘left’ and ‘right’ regions labelled ‘1’ and ‘2’, respectively, and take a discontinuous jump at the junction between these regions. The sharp boundary limit gives solutions in the asymptotic limit
![]() $k_{y}L_{v}\ll 1$
where
$k_{y}L_{v}\ll 1$
where
![]() $L_{v}$
is the gradient scale length of the velocity profile, i.e. the width of the velocity transition layer where the jumps take place. Extrapolation of the sharp boundary results to
$L_{v}$
is the gradient scale length of the velocity profile, i.e. the width of the velocity transition layer where the jumps take place. Extrapolation of the sharp boundary results to
![]() $k_{y}L_{v}\sim 0.5$
gives a rough estimate of the maximum growth, optimized over
$k_{y}L_{v}\sim 0.5$
gives a rough estimate of the maximum growth, optimized over
![]() $k_{y}$
, of the KH mode. In the local limit
$k_{y}$
, of the KH mode. In the local limit
![]() $k_{y}L_{v}\gg 1$
the KH mode is stable because of the instability cutoff at
$k_{y}L_{v}\gg 1$
the KH mode is stable because of the instability cutoff at
![]() $k_{max}L_{v}\sim 1$
. These latter points will also be demonstrated in the numerical work of § 3.
$k_{max}L_{v}\sim 1$
. These latter points will also be demonstrated in the numerical work of § 3.
The first integral of (2.11) for
![]() $x\leqslant x_{2}$
is
$x\leqslant x_{2}$
is
Here the integral on the right-hand side is across the layer of width
![]() $L_{v}$
separating the two regions. In the sharp boundary asymptotic limit, this layer width shrinks to zero. Since the integrand itself remains finite, the integral evaluates to zero asymptotically. Evaluating (2.13) at
$L_{v}$
separating the two regions. In the sharp boundary asymptotic limit, this layer width shrinks to zero. Since the integrand itself remains finite, the integral evaluates to zero asymptotically. Evaluating (2.13) at
![]() $x=x_{2}$
shows that the left-hand side must be the same in the two regions. Since
$x=x_{2}$
shows that the left-hand side must be the same in the two regions. Since
![]() $\tilde{{\it\omega}}$
is constant in any given region, we have from (2.13)
$\tilde{{\it\omega}}$
is constant in any given region, we have from (2.13)
Equation (2.13) can also be expressed as
where
![]() $C$
is a constant. Since
$C$
is a constant. Since
![]() $\tilde{{\it\omega}}A$
is finite though discontinuous,
$\tilde{{\it\omega}}A$
is finite though discontinuous,
![]() ${\it\delta}{\it\Phi}/\tilde{{\it\omega}}$
must be continuous across the junction (as with the first integral, the integration of
${\it\delta}{\it\Phi}/\tilde{{\it\omega}}$
must be continuous across the junction (as with the first integral, the integration of
![]() $C/\tilde{{\it\omega}}A$
vanishes asymptotically)
$C/\tilde{{\it\omega}}A$
vanishes asymptotically)
Combining (2.14) and (2.16) yields the jump condition on the logarithmic derivative
The next step is to solve (2.11) in regions 1 and 2 to obtain the logarithmic derivatives on the two sides and do the matching. Since
![]() $\tilde{{\it\omega}}$
and
$\tilde{{\it\omega}}$
and
![]() $A$
are constants within each region the solutions are exponential and the branches that decay at infinity are
$A$
are constants within each region the solutions are exponential and the branches that decay at infinity are
or on employing the definition of
![]() $A$
$A$
This is the primary result of the analytic model. By choice of frame, we can take
![]() $v_{y1}=V/2$
,
$v_{y1}=V/2$
,
![]() $v_{y2}=-V/2$
where
$v_{y2}=-V/2$
where
![]() $V$
is the total jump in velocity across the layer. Then, normalizing
$V$
is the total jump in velocity across the layer. Then, normalizing
![]() ${\it\omega}$
to
${\it\omega}$
to
![]() $k_{y}V$
and defining
$k_{y}V$
and defining
Note that
![]() ${\it\tau}$
is just the ratio of the ion diamagnetic velocity to the total jump in
${\it\tau}$
is just the ratio of the ion diamagnetic velocity to the total jump in
![]() $\boldsymbol{E}\times \boldsymbol{B}$
velocity and
$\boldsymbol{E}\times \boldsymbol{B}$
velocity and
![]() ${\it\beta}$
is proportional to the strength of the Alfvén parallel current.
${\it\beta}$
is proportional to the strength of the Alfvén parallel current.
2.3 Sharp boundary model results
We first consider the effects of a density gradient, ion diamagnetism and Alfvén parallel current separately. For a pure density gradient (
![]() ${\it\tau}={\it\beta}=0$
), (2.24) reduces to
${\it\tau}={\it\beta}=0$
), (2.24) reduces to
where
![]() $-1<{\it\Delta}<1$
is given by
$-1<{\it\Delta}<1$
is given by
i.e.
![]() $n_{1}=1-{\it\Delta}$
and
$n_{1}=1-{\it\Delta}$
and
![]() $n_{2}=1+{\it\Delta}$
so that
$n_{2}=1+{\it\Delta}$
so that
![]() ${\it\Delta}$
is proportional to the density gradient,
${\it\Delta}$
is proportional to the density gradient,
![]() $\text{d}n/\text{d}x\sim n{\it\Delta}/L$
where
$\text{d}n/\text{d}x\sim n{\it\Delta}/L$
where
![]() $2L$
is the scale length over which
$2L$
is the scale length over which
![]() $n$
transitions from
$n$
transitions from
![]() $n_{1}$
to
$n_{1}$
to
![]() $n_{2}$
. The solution is
$n_{2}$
. The solution is
The growth rate of (2.27) is maximized for
![]() ${\it\Delta}=0$
. Thus any density gradient (in either direction) reduces the growth rate of the KH mode in this limit. Similar results were obtained by Wang et al. (Reference Wang, Xue, Ye and Li2009). Physically it is clear that for
${\it\Delta}=0$
. Thus any density gradient (in either direction) reduces the growth rate of the KH mode in this limit. Similar results were obtained by Wang et al. (Reference Wang, Xue, Ye and Li2009). Physically it is clear that for
![]() $|{\it\Delta}|=1$
, i.e. vanishing
$|{\it\Delta}|=1$
, i.e. vanishing
![]() $n_{1}$
or
$n_{1}$
or
![]() $n_{2}$
, there is no inertial weighting of vorticity on one side of the velocity jump, hence there is no KH instability.
$n_{2}$
, there is no inertial weighting of vorticity on one side of the velocity jump, hence there is no KH instability.
Next, with
![]() ${\it\Delta}={\it\beta}=0$
, (2.24) gives the effect of ion diamagnetism as
${\it\Delta}={\it\beta}=0$
, (2.24) gives the effect of ion diamagnetism as
If
![]() ${\it\tau}_{1}={\it\tau}_{2}\equiv {\it\tau}$
the result is
${\it\tau}_{1}={\it\tau}_{2}\equiv {\it\tau}$
the result is
which gives stability for either sign of
![]() ${\it\tau}$
when
${\it\tau}$
when
![]() $|{\it\tau}|>1$
. This result is consistent with Rogers & Dorland (Reference Rogers and Dorland2005) who show (in the present notation) that
$|{\it\tau}|>1$
. This result is consistent with Rogers & Dorland (Reference Rogers and Dorland2005) who show (in the present notation) that
![]() ${\it\tau}<-1$
guarantees stability (or equivalently that
${\it\tau}<-1$
guarantees stability (or equivalently that
![]() ${\it\tau}>-1$
is a necessary condition for instability). The real part of
${\it\tau}>-1$
is a necessary condition for instability). The real part of
![]() ${\it\omega}$
is shifted by the ion diamagnetic drift as expected.
${\it\omega}$
is shifted by the ion diamagnetic drift as expected.
Since
![]() ${\it\tau}\propto p_{i}^{\prime }$
considering
${\it\tau}\propto p_{i}^{\prime }$
considering
![]() ${\it\tau}_{1}\neq {\it\tau}_{2}$
describes the effects of
${\it\tau}_{1}\neq {\it\tau}_{2}$
describes the effects of
![]() $p_{i}^{\prime \prime }$
. The stability condition from (2.28) is
$p_{i}^{\prime \prime }$
. The stability condition from (2.28) is
Stability is attained at smaller values of the mean diamagnetic parameter
![]() $({\it\tau}_{1}+{\it\tau}_{2})/2$
when
$({\it\tau}_{1}+{\it\tau}_{2})/2$
when
![]() ${\it\tau}_{1}<{\it\tau}_{2}$
. To express this result in a more physical way, it is simplest to consider
${\it\tau}_{1}<{\it\tau}_{2}$
. To express this result in a more physical way, it is simplest to consider
![]() $V>0$
, i.e.
$V>0$
, i.e.
![]() $\partial _{x}v_{E}<0$
. Then
$\partial _{x}v_{E}<0$
. Then
![]() ${\it\tau}_{1}<{\it\tau}_{2}$
implies
${\it\tau}_{1}<{\it\tau}_{2}$
implies
![]() $\partial _{x}v_{di}>0$
. This case reduces the shear of the net flow,
$\partial _{x}v_{di}>0$
. This case reduces the shear of the net flow,
![]() $\partial _{x}(v_{E}+v_{di})$
.
$\partial _{x}(v_{E}+v_{di})$
.
Retaining
![]() ${\it\beta}$
with
${\it\beta}$
with
![]() ${\it\Delta}={\it\tau}=0$
yields
${\it\Delta}={\it\tau}=0$
yields
or
which shows that the Alfvén parallel current stabilizes the KH mode for
![]() ${\it\beta}^{2}>1/2$
. Since
${\it\beta}^{2}>1/2$
. Since
![]() ${\it\beta}$
has an explicit
${\it\beta}$
has an explicit
![]() $1/k_{y}^{2}$
dependence, this result implies that there is a threshold
$1/k_{y}^{2}$
dependence, this result implies that there is a threshold
![]() $k_{y}$
below which KH modes are absolutely stable. This will be confirmed in the numerical results of § 3. Note that
$k_{y}$
below which KH modes are absolutely stable. This will be confirmed in the numerical results of § 3. Note that
![]() ${\it\beta}\propto k_{\Vert }$
so that magnetic shear, which naturally provides a finite
${\it\beta}\propto k_{\Vert }$
so that magnetic shear, which naturally provides a finite
![]() $k_{\Vert }$
for these radially extended modes, enhances the stabilization effect (Rogers & Dorland Reference Rogers and Dorland2005).
$k_{\Vert }$
for these radially extended modes, enhances the stabilization effect (Rogers & Dorland Reference Rogers and Dorland2005).
Finally, we can consider the combined effects of a density gradient, ion diamagnetism and the Alfvén parallel current. The condition for stability is
where for simplicity
![]() ${\it\tau}_{1}={\it\tau}_{2}\equiv {\it\tau}$
. Notice that when
${\it\tau}_{1}={\it\tau}_{2}\equiv {\it\tau}$
. Notice that when
![]() ${\it\tau}={\it\Delta}$
their effects cancel, thus the density gradient counteracts part of the ion pressure gradient. Qualitatively it is as if the net result is more sensitive to the ion temperature gradient part of
${\it\tau}={\it\Delta}$
their effects cancel, thus the density gradient counteracts part of the ion pressure gradient. Qualitatively it is as if the net result is more sensitive to the ion temperature gradient part of
![]() $p_{i}^{\prime }$
. A more rigorous general statement is not possible because in the sharp boundary model the density and ion pressure gradients do not enter in the same way. In fact, although
$p_{i}^{\prime }$
. A more rigorous general statement is not possible because in the sharp boundary model the density and ion pressure gradients do not enter in the same way. In fact, although
![]() ${\it\tau}$
describes ion diamagnetic effects,
${\it\tau}$
describes ion diamagnetic effects,
![]() ${\it\Delta}$
may be best associated with the inertial weighting of the vorticity rather than a density gradient drift. Further investigation of this point would require a diffuse profile model. A marginal stability diagram is shown in figure 2.
${\it\Delta}$
may be best associated with the inertial weighting of the vorticity rather than a density gradient drift. Further investigation of this point would require a diffuse profile model. A marginal stability diagram is shown in figure 2.

Figure 2. Marginal stability diagram for the dispersion relation of (2.24) with
![]() ${\it\tau}_{1}={\it\tau}_{2}\equiv {\it\tau}$
. Note that in the presence of a density gradient, the effect of an ion pressure gradient depends on its sign.
${\it\tau}_{1}={\it\tau}_{2}\equiv {\it\tau}$
. Note that in the presence of a density gradient, the effect of an ion pressure gradient depends on its sign.
3 The KH mode in realistic toroidal geometry
While useful for illustrating the effects of a density gradient, ion diamagnetism and the Alfvén parallel current on the KH mode, the analytic model cannot directly account for the effects of magnetic shear or realistic toroidal geometry. For this we turn to numerical modelling using the 2DX eigenvalue code (Baver et al. Reference Baver, Myra and Umansky2011) together with a minimal (cold ion) physics model for the KH mode. Our goal is again physical insight rather than comprehensive modelling that includes all effects simultaneously. Comprehensive tokamak gyro-kinetic models, at least for the closed flux surface regions, have been discussed previously (Rogers & Dorland Reference Rogers and Dorland2005; Wang et al. Reference Wang, Ethier, Ren, Kaye, Chen, Startsev, Lu and Li2015).
The 2DX code solves linearized eigenvalue problems in the
![]() $R$
–
$R$
–
![]() $Z$
plane for each toroidal mode number
$Z$
plane for each toroidal mode number
![]() $n$
. It takes as input experimental magnetic divertor geometry for the edge and SOL and implements toroidal periodicity on both the open and closed flux surfaces while allowing separatrix spanning modes. 2DX has a specialized equation parser to input the physics model and associated plasma profiles. Use of a sparse matrix package enables high resolution. More details and some code benchmark cases are given by Baver et al. (Reference Baver, Myra and Umansky2011).
$n$
. It takes as input experimental magnetic divertor geometry for the edge and SOL and implements toroidal periodicity on both the open and closed flux surfaces while allowing separatrix spanning modes. 2DX has a specialized equation parser to input the physics model and associated plasma profiles. Use of a sparse matrix package enables high resolution. More details and some code benchmark cases are given by Baver et al. (Reference Baver, Myra and Umansky2011).
Typically a field line following coordinate system is employed in 2DX. The mode is described as
where (
![]() ${\it\psi}$
,
${\it\psi}$
,
![]() ${\it\theta}$
,
${\it\theta}$
,
![]() ${\it\zeta}$
) are respectively the poloidal magnetic flux ‘radial’ variable, a poloidal angle variable and the toroidal angle;
${\it\zeta}$
) are respectively the poloidal magnetic flux ‘radial’ variable, a poloidal angle variable and the toroidal angle;
![]() $n_{{\it\zeta}}$
is the toroidal mode number and
$n_{{\it\zeta}}$
is the toroidal mode number and
![]() ${\it\nu}$
is the local magnetic shear. By extracting the eikonal function as shown in (3.1), is it only necessary to carry out a numerical solution for the slowly varying envelope function
${\it\nu}$
is the local magnetic shear. By extracting the eikonal function as shown in (3.1), is it only necessary to carry out a numerical solution for the slowly varying envelope function
![]() ${\it\delta}{\it\phi}$
. The exponential containing the eikonal piece may be used to define a local
${\it\delta}{\it\phi}$
. The exponential containing the eikonal piece may be used to define a local
![]() $\boldsymbol{k}_{\bot }({\it\psi},{\it\theta})$
given
$\boldsymbol{k}_{\bot }({\it\psi},{\it\theta})$
given
![]() $n_{{\it\zeta}}$
and the magnetic geometry; however, no eikonal approximation is involved since the residual eigenmode structure is contained in
$n_{{\it\zeta}}$
and the magnetic geometry; however, no eikonal approximation is involved since the residual eigenmode structure is contained in
![]() ${\it\delta}{\it\phi}$
. The so-called ballooning angle
${\it\delta}{\it\phi}$
. The so-called ballooning angle
![]() ${\it\theta}_{0}$
is usually taken to be at the outboard midplane.
${\it\theta}_{0}$
is usually taken to be at the outboard midplane.
For the purposes of this section we employ a minimal physics model, which neglects ion pressure and employs constant density and electron pressure, to eliminate curvature-driven modes and allow focus on the effects of parallel currents and geometry on the KH mode. The model retains parallel collisional and electron skin effects. The linearized model equations for the perturbed vorticity
![]() ${\it\delta}{\it\varpi}$
, pressure
${\it\delta}{\it\varpi}$
, pressure
![]() ${\it\delta}p$
and parallel vector potential
${\it\delta}p$
and parallel vector potential
![]() ${\it\delta}A$
are
${\it\delta}A$
are
To most efficiently present the numerical results it is useful first to carry out an invariant scaling analysis (Connor & Taylor Reference Connor and Taylor1984) of (3.2) and (3.3) in an effort to reduce the parameter space to a minimal set of dimensionless combinations. For the purpose of this scaling analysis alone, one may combine the equations into a single heuristic equation by eliminating
![]() ${\it\delta}A$
. Employing the notation
${\it\delta}A$
. Employing the notation
![]() $1/L$
for
$1/L$
for
![]() $\boldsymbol{{\rm\nabla}}_{\bot }$
acting on equilibrium quantities and
$\boldsymbol{{\rm\nabla}}_{\bot }$
acting on equilibrium quantities and
![]() $k_{\bot }$
for
$k_{\bot }$
for
![]() $\boldsymbol{{\rm\nabla}}_{\bot }$
acting on perturbed quantities we find that the scaling is determined by
$\boldsymbol{{\rm\nabla}}_{\bot }$
acting on perturbed quantities we find that the scaling is determined by
where the
![]() $\boldsymbol{b}\times$
is irrelevant for the scaling argument. Here we have introduced
$\boldsymbol{b}\times$
is irrelevant for the scaling argument. Here we have introduced
![]() ${\it\omega}_{a}=B{\it\mu}^{1/2}{\it\delta}_{e}/(n^{1/2}R)\equiv v_{a}/R$
where for the purpose of scaling, we can set
${\it\omega}_{a}=B{\it\mu}^{1/2}{\it\delta}_{e}/(n^{1/2}R)\equiv v_{a}/R$
where for the purpose of scaling, we can set
![]() $k_{\Vert }=1/R$
.
$k_{\Vert }=1/R$
.
Ab initio there are six input parameters
The formal procedure is to postulate a transformation of the form
![]() ${\it\gamma}\rightarrow {\it\lambda}{\it\gamma}$
,
${\it\gamma}\rightarrow {\it\lambda}{\it\gamma}$
,
![]() $k_{\bot }\rightarrow {\it\lambda}^{a}k_{\bot },v\rightarrow {\it\lambda}^{b}v$
,
$k_{\bot }\rightarrow {\it\lambda}^{a}k_{\bot },v\rightarrow {\it\lambda}^{b}v$
,
![]() $L\rightarrow {\it\lambda}^{c}L$
,
$L\rightarrow {\it\lambda}^{c}L$
,
![]() ${\it\omega}_{a}^{2}\rightarrow {\it\lambda}^{d}{\it\omega}_{a}^{2}$
,
${\it\omega}_{a}^{2}\rightarrow {\it\lambda}^{d}{\it\omega}_{a}^{2}$
,
![]() ${\it\delta}_{e}^{2}\rightarrow {\it\lambda}^{e}{\it\delta}_{e}^{2}$
,
${\it\delta}_{e}^{2}\rightarrow {\it\lambda}^{e}{\it\delta}_{e}^{2}$
,
![]() ${\it\nu}_{e}\rightarrow {\it\lambda}^{f}{\it\nu}_{e}$
and look for a solution (
${\it\nu}_{e}\rightarrow {\it\lambda}^{f}{\it\nu}_{e}$
and look for a solution (
![]() $a,b,c,d,e,f$
) that leaves the original equations, equivalently (3.4) invariant: all powers of
$a,b,c,d,e,f$
) that leaves the original equations, equivalently (3.4) invariant: all powers of
![]() ${\it\lambda}$
should collect up and cancel out. The resulting equations are
${\it\lambda}$
should collect up and cancel out. The resulting equations are
![]() $a+b=1$
,
$a+b=1$
,
![]() $1+2a=a-2c+b$
,
$1+2a=a-2c+b$
,
![]() $1+2a=e+2a-1$
,
$1+2a=e+2a-1$
,
![]() $2a+f=0$
and
$2a+f=0$
and
![]() $g=1$
which have as the solution
$g=1$
which have as the solution
![]() $b=1-a$
,
$b=1-a$
,
![]() $c=-a$
,
$c=-a$
,
![]() $e=2$
,
$e=2$
,
![]() $f=-2a$
and
$f=-2a$
and
![]() $g=1$
with one free parameter
$g=1$
with one free parameter
![]() $a$
. There are two independent invariant transformations given by
$a$
. There are two independent invariant transformations given by
![]() $a=0,1$
.
$a=0,1$
.
This reduces the original six input parameters to four invariant combinations which may be taken as
with
![]() $F$
a function to be determined numerically. These four invariant combinations completely characterize the KH mode aside from the geometry, which includes the magnetic flux geometry of the torus and the profile of the equilibrium electrostatic potential
$F$
a function to be determined numerically. These four invariant combinations completely characterize the KH mode aside from the geometry, which includes the magnetic flux geometry of the torus and the profile of the equilibrium electrostatic potential
![]() ${\it\Phi}({\it\psi})$
. We take the latter to be a flux function given by
${\it\Phi}({\it\psi})$
. We take the latter to be a flux function given by
where
![]() ${\it\Phi}_{1}^{\prime },{\it\Phi}_{2}^{\prime },{\it\psi}_{{\it\Phi}0},{\it\psi}_{w}$
are constants that specify the velocity
${\it\Phi}_{1}^{\prime },{\it\Phi}_{2}^{\prime },{\it\psi}_{{\it\Phi}0},{\it\psi}_{w}$
are constants that specify the velocity
![]() $v$
, scale length
$v$
, scale length
![]() $L$
and location of the shear layer relative to the separatrix. The invariant parameters are defined with
$L$
and location of the shear layer relative to the separatrix. The invariant parameters are defined with
![]() $v$
as the total jump in
$v$
as the total jump in
![]() $\boldsymbol{E}\times \boldsymbol{B}$
velocity implied by (3.7) and the scale length given as
$\boldsymbol{E}\times \boldsymbol{B}$
velocity implied by (3.7) and the scale length given as
![]() $L={\it\psi}_{w}/(RB_{p})$
where
$L={\it\psi}_{w}/(RB_{p})$
where
![]() $R$
is the major radius of the torus and
$R$
is the major radius of the torus and
![]() $B_{p}$
is the local poloidal magnetic field.
$B_{p}$
is the local poloidal magnetic field.

Figure 3. (a) Flux surface geometry showing the computational grid at reduced resolution for purposes of illustration; (b) typical KH eigenmode structure of
![]() $|{\it\delta}{\it\Phi}|$
showing localization to the outboard midplane and a double peak.
$|{\it\delta}{\it\Phi}|$
showing localization to the outboard midplane and a double peak.
Figure 3 illustrates the NSTX (Ono et al.
Reference Ono, Kaye, Peng, Barnes, Blanchard, Carter, Chrzanowski, Dudek, Ewig and Gates2000) flux surface geometry used for this study and the spatial structure of a typical KH eigenmode on the computation mesh. Parameters for this case are
![]() ${\it\omega}_{a}L/v=0.108$
,
${\it\omega}_{a}L/v=0.108$
,
![]() ${\it\delta}_{e}/L=0.24$
,
${\it\delta}_{e}/L=0.24$
,
![]() ${\it\nu}_{e}L/v=0.36$
and
${\it\nu}_{e}L/v=0.36$
and
![]() $n_{{\it\zeta}}=100$
which implies
$n_{{\it\zeta}}=100$
which implies
![]() $k_{b}L=0.40$
. Here
$k_{b}L=0.40$
. Here
![]() $k_{b}$
is the binormal component of
$k_{b}$
is the binormal component of
![]() $\boldsymbol{k}_{\bot }$
at the outboard midplane, which is also
$\boldsymbol{k}_{\bot }$
at the outboard midplane, which is also
![]() $|k_{\bot }|$
at that location. Note that the mode strongly balloons near the outboard midplane of the torus. At first this may seem surprising since, unlike curvature-driven ballooning modes, the free energy from (3.7) is not obviously localized to this region. The localization results from the weighting provided by the
$|k_{\bot }|$
at that location. Note that the mode strongly balloons near the outboard midplane of the torus. At first this may seem surprising since, unlike curvature-driven ballooning modes, the free energy from (3.7) is not obviously localized to this region. The localization results from the weighting provided by the
![]() $RB_{p}$
Jacobian factors in the equilibrium vorticity gradient
$RB_{p}$
Jacobian factors in the equilibrium vorticity gradient
The
![]() $R$
factor weights the outboard side of the torus relative to the inboard side and the
$R$
factor weights the outboard side of the torus relative to the inboard side and the
![]() $B_{p}$
factor weights the midplane relative to the upper (virtual) and lower X-points. To understand this in a more physical way, consider the equilibrium electric field between two adjacent flux surfaces,
$B_{p}$
factor weights the midplane relative to the upper (virtual) and lower X-points. To understand this in a more physical way, consider the equilibrium electric field between two adjacent flux surfaces,
![]() $E_{{\it\theta}}=-{\rm\Delta}{\it\Phi}/{\rm\Delta}r$
where
$E_{{\it\theta}}=-{\rm\Delta}{\it\Phi}/{\rm\Delta}r$
where
![]() ${\rm\Delta}r={\rm\Delta}{\it\psi}/RB_{p}$
is the local flux surface spacing. Because the flux surface spacing is smallest at the outboard midplane (see figure 3
a) the
${\rm\Delta}r={\rm\Delta}{\it\psi}/RB_{p}$
is the local flux surface spacing. Because the flux surface spacing is smallest at the outboard midplane (see figure 3
a) the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
drift velocity from
$\boldsymbol{E}\times \boldsymbol{B}$
drift velocity from
![]() $E_{{\it\theta}}$
, its shear, and hence the instability drive for the KH mode is largest there. This effect, while present for all tokamaks, is accentuated in the high-plasma-beta spherical torus geometry.
$E_{{\it\theta}}$
, its shear, and hence the instability drive for the KH mode is largest there. This effect, while present for all tokamaks, is accentuated in the high-plasma-beta spherical torus geometry.
The eigenmode illustrated in the right panel of figure 3 shows a double peaked structure for
![]() $|{\it\delta}{\it\Phi}|$
. Further investigation reveals that the maxima of
$|{\it\delta}{\it\Phi}|$
. Further investigation reveals that the maxima of
![]() $\text{Re}({\it\Phi})$
and
$\text{Re}({\it\Phi})$
and
![]() $\text{Im}({\it\Phi})$
are shifted spatially with respect to each other as a result of an outward propagating radial phase velocity for the unstable modes. The structure shown in figure 3 is typical of all the results summarized in the following.
$\text{Im}({\it\Phi})$
are shifted spatially with respect to each other as a result of an outward propagating radial phase velocity for the unstable modes. The structure shown in figure 3 is typical of all the results summarized in the following.
Table 1. Parameters employed for the cases shown in figure 4.

a
![]() ${\it\omega}_{a}L^{2}/(v{\it\delta}_{e})=0.073$
.
${\it\omega}_{a}L^{2}/(v{\it\delta}_{e})=0.073$
.
Figure 4 illustrates the dependence of the KH growth rate on wavenumber for a few different combinations of dimensionless parameters (see table 1). The case labelled ‘base (EM Alfvén)’ shows the unstable spectrum with all effects: electromagnetic (EM) parallel Alfvén current, collisionality and electron skin. Note that there is both a lower and an upper limit on
![]() $k_{b}L$
for instability. The upper limit is essentially that of the classical KH mode, to be discussed next; the lower limit is as expected from the analysis of § 2, (2.23) and (2.32) which show that the stabilizing effects of the EM parallel current are relatively stronger for small perpendicular wavenumbers.
$k_{b}L$
for instability. The upper limit is essentially that of the classical KH mode, to be discussed next; the lower limit is as expected from the analysis of § 2, (2.23) and (2.32) which show that the stabilizing effects of the EM parallel current are relatively stronger for small perpendicular wavenumbers.
The strong stabilizing effect of the parallel Alfvén current is illustrated by comparison of the base case with the electrostatic (ES) curve labelled ‘classical ES KH’. In this case, we have
![]() ${\it\omega}_{a}=0$
, and
${\it\omega}_{a}=0$
, and
![]() ${\it\delta}_{e}$
and
${\it\delta}_{e}$
and
![]() ${\it\nu}_{e}$
become irrelevant. This spectrum shows the inverted-parabolic growth rate dependence that is characteristic of the pure KH mode (see figure 1 and its discussion). In this case the corresponding fastest-growing eigenmodes have a delta-function character in their
${\it\nu}_{e}$
become irrelevant. This spectrum shows the inverted-parabolic growth rate dependence that is characteristic of the pure KH mode (see figure 1 and its discussion). In this case the corresponding fastest-growing eigenmodes have a delta-function character in their
![]() ${\it\theta}$
-variation along the field line: there is no line-bending energy cost when
${\it\theta}$
-variation along the field line: there is no line-bending energy cost when
![]() ${\it\omega}_{a}=0$
. The dashed line in figure 4 labelled ‘
${\it\omega}_{a}=0$
. The dashed line in figure 4 labelled ‘
![]() $k_{b}L\ll 1$
analytic’ is the asymptotic result from the sharp boundary model of § 2 applied to this case. Agreement for sufficiently small
$k_{b}L\ll 1$
analytic’ is the asymptotic result from the sharp boundary model of § 2 applied to this case. Agreement for sufficiently small
![]() $k_{b}L$
is good and provides a check on the numerical work.
$k_{b}L$
is good and provides a check on the numerical work.
The curve labelled ‘ES limit’ shows the result when the parameter
![]() ${\it\delta}_{e}/L$
is asymptotically large. Referring to (3.5), and noting that
${\it\delta}_{e}/L$
is asymptotically large. Referring to (3.5), and noting that
![]() ${\it\omega}_{a}\propto {\it\delta}_{e}$
, in this limit the Alfvén parameter that remains is
${\it\omega}_{a}\propto {\it\delta}_{e}$
, in this limit the Alfvén parameter that remains is
![]() ${\it\omega}_{a}L^{2}/(v{\it\delta}_{e})=L^{2}{\it\Omega}_{i}{\it\mu}^{1/2}/(Rv)$
where
${\it\omega}_{a}L^{2}/(v{\it\delta}_{e})=L^{2}{\it\Omega}_{i}{\it\mu}^{1/2}/(Rv)$
where
![]() ${\it\Omega}_{i}=eB/(m_{i}c)$
(see table 1). This is an electrostatic limit, but one that retains parallel currents. These ES parallel currents are also stabilizing relative to the
${\it\Omega}_{i}=eB/(m_{i}c)$
(see table 1). This is an electrostatic limit, but one that retains parallel currents. These ES parallel currents are also stabilizing relative to the
![]() ${\it\omega}_{a}=0$
case. Finally, the curve labelled ‘half
${\it\omega}_{a}=0$
case. Finally, the curve labelled ‘half
![]() ${\it\nu}_{e}$
’ shows that collisionality did not play a strong role in our base case and that reducing
${\it\nu}_{e}$
’ shows that collisionality did not play a strong role in our base case and that reducing
![]() ${\it\nu}_{e}$
tends to increase the growth rates of the higher
${\it\nu}_{e}$
tends to increase the growth rates of the higher
![]() $k_{b}$
modes. None of the preceding parameter variations have much effect on the spectral cutoff at high
$k_{b}$
modes. None of the preceding parameter variations have much effect on the spectral cutoff at high
![]() $k$
. These cases confirm the stabilizing effect of both EM and ES perturbed parallel currents on the KH mode.
$k$
. These cases confirm the stabilizing effect of both EM and ES perturbed parallel currents on the KH mode.
The cases shown in figure 4 highlight the main effects of the invariant dimensionless parameter combinations. It remains to assess the role of magnetic geometry, in particular in the vicinity of the separatrix, including both closed and open field line regions. To explore this, figure 5 shows the results of a study in which the location of the sheared flow layer, parametrized by
![]() ${\it\psi}_{{\it\Phi}0}$
is varied with respect to the separatrix. Negative (positive) shifts indicate cases where
${\it\psi}_{{\it\Phi}0}$
is varied with respect to the separatrix. Negative (positive) shifts indicate cases where
![]() ${\it\psi}_{{\it\Phi}0}$
is located in the closed (open) flux surface region. All other parameters are held fixed. It is seen that the KH mode is more unstable at, and just outside of, the separatrix compared with inside the closed surface region. The reason appears to be related to the distribution of magnetic shear.
${\it\psi}_{{\it\Phi}0}$
is located in the closed (open) flux surface region. All other parameters are held fixed. It is seen that the KH mode is more unstable at, and just outside of, the separatrix compared with inside the closed surface region. The reason appears to be related to the distribution of magnetic shear.

Figure 5. Dependence of the KH spectrum growth rate on location of the velocity shear layer relative to the separatrix. Negative (positive) shifts indicate cases where the sheared flow layer is located in the closed (open) flux surface region.
Figure 6 shows the variation of the integrated magnetic shear
![]() $k_{{\it\psi}}\propto \int _{{\it\theta}_{0}}^{{\it\theta}}\text{d}{\it\theta}\partial {\it\nu}/\partial {\it\psi}$
along the field line at the flux surface of strongest velocity shear for the four cases considered in figure 5. The most unstable modes have reduced magnetic shear in the midplane region and stronger shear near the X-points, especially the lower (dominant) X-point near
$k_{{\it\psi}}\propto \int _{{\it\theta}_{0}}^{{\it\theta}}\text{d}{\it\theta}\partial {\it\nu}/\partial {\it\psi}$
along the field line at the flux surface of strongest velocity shear for the four cases considered in figure 5. The most unstable modes have reduced magnetic shear in the midplane region and stronger shear near the X-points, especially the lower (dominant) X-point near
![]() ${\it\theta}=2{\rm\pi}$
. The important role of the poloidal distribution of local magnetic shear in shaped plasmas has been noted previously in a variety of contexts (Myra et al.
Reference Myra, D’Ippolito, Xu and Cohen2000; Sugiyama & Strauss Reference Sugiyama and Strauss2010; Xu et al.
Reference Xu, Dudson, Snyder, Umansky, Wilson and Casper2011).
${\it\theta}=2{\rm\pi}$
. The important role of the poloidal distribution of local magnetic shear in shaped plasmas has been noted previously in a variety of contexts (Myra et al.
Reference Myra, D’Ippolito, Xu and Cohen2000; Sugiyama & Strauss Reference Sugiyama and Strauss2010; Xu et al.
Reference Xu, Dudson, Snyder, Umansky, Wilson and Casper2011).

Figure 6. Distribution of integrated magnetic shear along a field line. The cases and colour scheme correspond to those of figure 5. The low-field-side region corresponds to
![]() ${\rm\pi}<{\it\theta}<2{\rm\pi}$
with the upper X-point at
${\rm\pi}<{\it\theta}<2{\rm\pi}$
with the upper X-point at
![]() ${\rm\pi}$
and the lower dominant X-point at
${\rm\pi}$
and the lower dominant X-point at
![]() $2{\rm\pi}$
.
$2{\rm\pi}$
.
4 Reduced modelling equations
The final topic considered in this paper is that of constructing reduced 2-D modelling equations that are at least qualitatively faithful to the physics of the KH mode discussed in this paper. In a 2-D interchange model, which simulates dynamics in the plane perpendicular to
![]() $\boldsymbol{B}$
, such as employed in the SOLT (Scrape-Off Layer Turbulence) code (Russell et al.
Reference Russell, D’Ippolito, Myra, Canik, Gray and Zweben2015), the transverse KH mode may easily be unstable. Strong
$\boldsymbol{B}$
, such as employed in the SOLT (Scrape-Off Layer Turbulence) code (Russell et al.
Reference Russell, D’Ippolito, Myra, Canik, Gray and Zweben2015), the transverse KH mode may easily be unstable. Strong
![]() $\boldsymbol{E}\times \boldsymbol{B}$
velocity shear layers can arise from Reynolds-driven flows and steep ion pressure profiles. It is desirable to account for the stabilizing effects of parallel current and magnetic shear in these types of nonlinear 2-D interchange models. To explore this possibility, we again revert to a cold ion model for simplicity of presentation. This is motivated by noting that the parallel current and warm ion terms in the model of § 2 are not intertwined.
$\boldsymbol{E}\times \boldsymbol{B}$
velocity shear layers can arise from Reynolds-driven flows and steep ion pressure profiles. It is desirable to account for the stabilizing effects of parallel current and magnetic shear in these types of nonlinear 2-D interchange models. To explore this possibility, we again revert to a cold ion model for simplicity of presentation. This is motivated by noting that the parallel current and warm ion terms in the model of § 2 are not intertwined.
The most important physics may be captured by adding the electromagnetic terms for
![]() $J_{\Vert }$
by combining Ampere’s law
$J_{\Vert }$
by combining Ampere’s law
![]() $J_{\Vert }=-(c/4{\rm\pi}){\rm\nabla}_{\bot }^{2}A_{\Vert }$
and the resistive Ohm’s law
$J_{\Vert }=-(c/4{\rm\pi}){\rm\nabla}_{\bot }^{2}A_{\Vert }$
and the resistive Ohm’s law
![]() $E_{\Vert }=-\boldsymbol{{\rm\nabla}}_{\Vert }{\it\Phi}-(1/c)\partial A_{\Vert }/\partial t={\it\eta}_{\Vert }J_{\Vert }$
to obtain (in dimensional Gaussian units)
$E_{\Vert }=-\boldsymbol{{\rm\nabla}}_{\Vert }{\it\Phi}-(1/c)\partial A_{\Vert }/\partial t={\it\eta}_{\Vert }J_{\Vert }$
to obtain (in dimensional Gaussian units)
The vorticity equation in the 2-D model, (2.1), requires a closure equation for
![]() $\boldsymbol{{\rm\nabla}}_{\Vert }J_{\Vert }$
(Krasheninnikov, D’Ippolito & Myra Reference Krasheninnikov, D’Ippolito and Myra2008; D’Ippolito, Myra & Zweben Reference D’Ippolito, Myra and Zweben2011). One such closure is the high-beta blob closure original proposed by Krasheninnikov, Ryutov & Yu (Reference Krasheninnikov, Ryutov and Yu2004),
$\boldsymbol{{\rm\nabla}}_{\Vert }J_{\Vert }$
(Krasheninnikov, D’Ippolito & Myra Reference Krasheninnikov, D’Ippolito and Myra2008; D’Ippolito, Myra & Zweben Reference D’Ippolito, Myra and Zweben2011). One such closure is the high-beta blob closure original proposed by Krasheninnikov, Ryutov & Yu (Reference Krasheninnikov, Ryutov and Yu2004),
This can be obtained heuristically from (4.1) by postulating outgoing Alfvén waves so that
![]() $\partial /\partial t\rightarrow -\text{i}{\it\omega}=-\text{i}k_{\Vert }v_{a}$
, and on the right-hand side of (4.1)
$\partial /\partial t\rightarrow -\text{i}{\it\omega}=-\text{i}k_{\Vert }v_{a}$
, and on the right-hand side of (4.1)
![]() $\boldsymbol{{\rm\nabla}}_{\Vert }\rightarrow \text{i}k_{\Vert }$
. Dropping the
$\boldsymbol{{\rm\nabla}}_{\Vert }\rightarrow \text{i}k_{\Vert }$
. Dropping the
![]() ${\it\eta}_{\Vert }$
term and estimating the
${\it\eta}_{\Vert }$
term and estimating the
![]() $\boldsymbol{{\rm\nabla}}_{\Vert }$
operator in the left-hand side of (4.2) as the inverse parallel half-length of a blob filament,
$\boldsymbol{{\rm\nabla}}_{\Vert }$
operator in the left-hand side of (4.2) as the inverse parallel half-length of a blob filament,
![]() $L_{\Vert }/2$
, one arrives at the right-hand side of (4.2). This closure implies dissipation: vorticity is lost by the outgoing parallel Alfvén wave as the field line bulges out and bends as a result of the blob filament’s midplane motion. It can easily be shown that the corresponding linear dispersion relation including an interchange driving term is
$L_{\Vert }/2$
, one arrives at the right-hand side of (4.2). This closure implies dissipation: vorticity is lost by the outgoing parallel Alfvén wave as the field line bulges out and bends as a result of the blob filament’s midplane motion. It can easily be shown that the corresponding linear dispersion relation including an interchange driving term is
where
![]() ${\it\omega}_{a}=2v_{a}/L_{\Vert }$
and
${\it\omega}_{a}=2v_{a}/L_{\Vert }$
and
![]() ${\it\gamma}_{mhd}=c_{s}/(RL_{p})^{1/2}$
. Evidently (4.3) does not contain the Alfvén physics in (2.21) necessary to stabilize interchange or KH modes: a term proportional to
${\it\gamma}_{mhd}=c_{s}/(RL_{p})^{1/2}$
. Evidently (4.3) does not contain the Alfvén physics in (2.21) necessary to stabilize interchange or KH modes: a term proportional to
![]() ${\it\omega}_{a}^{2}$
is required.
${\it\omega}_{a}^{2}$
is required.
An alternative closure describing this physics is instead given by treating the time dynamics of (4.1) directly. A vorticity-Alfvén model which accomplishes this is given by
This model contains the necessary physics to stabilize interchange and KH modes by including the Alfvén wave line-bending energy.
For application in codes such as SOLT, it is useful to have a unified closure which automatically includes limiting cases as dictated by (dynamically evolving) plasma parameters. The EM Alfvén induction through
![]() $A_{\Vert }$
provides a channel for charge loss that is separate from (and effectively in parallel with) electrostatic charge loss to the sheath. As such, it is reasonable to add the parallel current closures. Let us postulate a combined closure and then discuss its justification:
$A_{\Vert }$
provides a channel for charge loss that is separate from (and effectively in parallel with) electrostatic charge loss to the sheath. As such, it is reasonable to add the parallel current closures. Let us postulate a combined closure and then discuss its justification:
where
![]() ${\it\omega}_{sh}=c_{s}/(k_{\bot }^{2}{\it\rho}_{s}^{2}L_{\Vert })$
is the sheath current term. It should be emphasized that this is a heuristic closure based on patching together asymptotic limits as discussed next.
${\it\omega}_{sh}=c_{s}/(k_{\bot }^{2}{\it\rho}_{s}^{2}L_{\Vert })$
is the sheath current term. It should be emphasized that this is a heuristic closure based on patching together asymptotic limits as discussed next.
It is clear that the
![]() ${\it\omega}_{a}=0$
limit of (4.8) and (4.9) recovers the previous electrostatic model. In the limit of small but finite
${\it\omega}_{a}=0$
limit of (4.8) and (4.9) recovers the previous electrostatic model. In the limit of small but finite
![]() ${\it\omega}_{a}\ll {\it\omega}$
(and for simplicity
${\it\omega}_{a}\ll {\it\omega}$
(and for simplicity
![]() ${\it\omega}_{sh}\ll {\it\omega}_{a}$
) there is no time for Alfvén physics to ‘equilibrate’ along field lines and as a result one gets line bending and dissipation from outgoing Alfvén waves. This is the high-beta blob regime of (4.3). Note that in this regime the inertial term dominates the Alfvén terms unless additional physics is present. X-point dissipation can provide the needed additional physics and allow the
${\it\omega}_{sh}\ll {\it\omega}_{a}$
) there is no time for Alfvén physics to ‘equilibrate’ along field lines and as a result one gets line bending and dissipation from outgoing Alfvén waves. This is the high-beta blob regime of (4.3). Note that in this regime the inertial term dominates the Alfvén terms unless additional physics is present. X-point dissipation can provide the needed additional physics and allow the
![]() $\text{i}{\it\omega}{\it\omega}_{a}$
term to directly balance the
$\text{i}{\it\omega}{\it\omega}_{a}$
term to directly balance the
![]() ${\it\gamma}_{mhd}^{2}$
interchange drive term (Myra & D’Ippolito Reference Myra and D’Ippolito2005).
${\it\gamma}_{mhd}^{2}$
interchange drive term (Myra & D’Ippolito Reference Myra and D’Ippolito2005).
In the limit
![]() ${\it\omega}_{a}\geqslant {\it\omega}$
Alfvén waves are no longer purely outgoing, rather there is time for them to sense the entire field line. In the absence of downstream dissipation they are reflected and result in Alfvén propagation in both directions, as in (4.6). Interchange and KH modes can be stabilized by the line-bending physics in this limit when
${\it\omega}_{a}\geqslant {\it\omega}$
Alfvén waves are no longer purely outgoing, rather there is time for them to sense the entire field line. In the absence of downstream dissipation they are reflected and result in Alfvén propagation in both directions, as in (4.6). Interchange and KH modes can be stabilized by the line-bending physics in this limit when
![]() ${\it\omega}_{a}>{\it\gamma}_{mhd}$
or
${\it\omega}_{a}>{\it\gamma}_{mhd}$
or
![]() ${\it\omega}_{a}>{\it\gamma}_{kh,max}\sim 0.2v_{y}^{\prime }$
, respectively.
${\it\omega}_{a}>{\it\gamma}_{kh,max}\sim 0.2v_{y}^{\prime }$
, respectively.
If the Alfvén parameter is in a particular range, then the model can describe a situation where the KH mode is stable, but curvature-driven interchange modes are unstable, viz.
Finally, these arguments, and the proposed model, can be used to estimate blob velocities in the various regimes using the dispersion relation in (4.9) with the blob velocity given by
where
![]() ${\it\delta}_{b}$
is the blob scale size in the poloidal direction.
${\it\delta}_{b}$
is the blob scale size in the poloidal direction.
5 Summary and conclusions
In § 2 of this paper we developed a unified analytical model for transverse KH modes in slab geometry including several physical ingredients: ion diamagnetism (including ion gyro-viscous terms), density gradients and parallel Alfvén currents. An exact, arbitrary wavenumber radial eigenvalue equation, following from (2.1)–(2.3), is given in (2.11) for this slab geometry case. The main result of the long-wavelength limit of the calculation is to be found in (2.21) or equivalently its normalized form (2.24). Taken one at a time, all the examined mechanisms have a stabilizing effect. Density gradients of either direction relative to the velocity shear reduce the growth rate of the KH mode, as shown in (2.27). Ion diamagnetism completely stabilizes the KH mode when it is sufficiently large, typically
![]() $|{\it\tau}|>1$
where
$|{\it\tau}|>1$
where
![]() ${\it\tau}\sim v_{di}/(v^{\prime }L_{v})$
, where
${\it\tau}\sim v_{di}/(v^{\prime }L_{v})$
, where
![]() $v_{di}$
is the diamagnetic drift velocity,
$v_{di}$
is the diamagnetic drift velocity,
![]() $v^{\prime }$
is the shearing rate of the
$v^{\prime }$
is the shearing rate of the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
velocity and
$\boldsymbol{E}\times \boldsymbol{B}$
velocity and
![]() $L_{v}$
is the width of the velocity shear layer. More precise conditions are discussed in connection with (2.29) and (2.30). Furthermore, when there is shear in the diamagnetic velocity, the case where the net velocity shear (ion diamagnetic plus
$L_{v}$
is the width of the velocity shear layer. More precise conditions are discussed in connection with (2.29) and (2.30). Furthermore, when there is shear in the diamagnetic velocity, the case where the net velocity shear (ion diamagnetic plus
![]() $\boldsymbol{E}\times \boldsymbol{B}$
) is minimized tends to be the most stable. Alfvén parallel currents completely stabilize the KH mode when
$\boldsymbol{E}\times \boldsymbol{B}$
) is minimized tends to be the most stable. Alfvén parallel currents completely stabilize the KH mode when
![]() $2{\it\omega}_{a}>k_{y}V$
where
$2{\it\omega}_{a}>k_{y}V$
where
![]() ${\it\omega}_{a}=k_{\Vert }v_{a}$
and
${\it\omega}_{a}=k_{\Vert }v_{a}$
and
![]() $V\sim v^{\prime }L_{v}$
, as shown in (2.32). When both density and ion pressure gradients coexist, as is usually the case in practice, the density gradient partly counteracts the ion pressure gradient, as discussed following (2.33).
$V\sim v^{\prime }L_{v}$
, as shown in (2.32). When both density and ion pressure gradients coexist, as is usually the case in practice, the density gradient partly counteracts the ion pressure gradient, as discussed following (2.33).
In the process of carrying out this work, we have also identified a new compact form for the ion gyro-viscous terms, as shown in appendix A. This form may prove convenient for future analytical and numerical studies. An arbitrary toroidal magnetic geometry generalization, not presented here, would also be useful.
Numerical results for the KH instability were considered in § 3 using a minimal physics model with cold ions and constant density, but realistic toroidal geometry. In general, KH modes in a torus balloon strongly to the outboard midplane side owing to the
![]() $RB_{p}$
weighting of the vorticity gradient when the equilibrium
$RB_{p}$
weighting of the vorticity gradient when the equilibrium
![]() ${\it\Phi}$
is a flux function, essentially a flux surface spacing effect. It was confirmed, for a typical spherical torus flux surface shape that magnetic geometry effects including magnetic shear and perturbed parallel currents have a strong stabilizing effect on the KH mode when
${\it\Phi}$
is a flux function, essentially a flux surface spacing effect. It was confirmed, for a typical spherical torus flux surface shape that magnetic geometry effects including magnetic shear and perturbed parallel currents have a strong stabilizing effect on the KH mode when
![]() $v_{a}L_{v}/(vR)\sim v_{a}/(v^{\prime }R)>1$
where
$v_{a}L_{v}/(vR)\sim v_{a}/(v^{\prime }R)>1$
where
![]() $v\sim v^{\prime }L_{v}$
is again the total jump in
$v\sim v^{\prime }L_{v}$
is again the total jump in
![]() $\boldsymbol{E}\times \boldsymbol{B}$
velocity across the shear layer. In addition to the usual KH instability cutoff at high
$\boldsymbol{E}\times \boldsymbol{B}$
velocity across the shear layer. In addition to the usual KH instability cutoff at high
![]() $k$
, electromagnetic Alfvén physics leads to a low-
$k$
, electromagnetic Alfvén physics leads to a low-
![]() $k$
limit for stability that is understood from the analytic model. Electrostatic limits for the parallel current were also found to be stabilizing, but without the low-
$k$
limit for stability that is understood from the analytic model. Electrostatic limits for the parallel current were also found to be stabilizing, but without the low-
![]() $k$
cutoff. The distribution of magnetic shear along the field lines was found to increase KH growth rates for situations when the shear layer is close to the separatrix or in the near SOL, as shown in figures 5 and 6.
$k$
cutoff. The distribution of magnetic shear along the field lines was found to increase KH growth rates for situations when the shear layer is close to the separatrix or in the near SOL, as shown in figures 5 and 6.
Finally, a set of equations with a parallel current closure, suitable for implementation in 2-D reduced modelling codes, was developed. Its relationship to the high-beta blob closure was discussed and it was shown that the main stabilizing effects of Alfvén parallel currents on interchange and KH modes could be captured by the reduced model.
The Kelvin–Helmholtz instability continues to be a fascinating topic in the dynamical evolution of plasmas. It will be important for tokamak plasma physics to continue the effort to understand its role in turbulence saturation physics and in the stability of edge and near SOL plasmas where gradient scale lengths can be extremely short. In particular, KH-driven turbulent transport and spreading of the narrow SOL heat flux channel would be very favourable to fusion.
Acknowledgement
This material is based upon work supported by the US Department of Energy Office of Science, Office of Fusion Energy Sciences under Award number DE-FG02-97ER54392.
Appendix A. Ion pressure contribution to the vorticity equation
In this appendix, we demonstrate the equivalence of three forms of the vorticity equation including ion pressure and ion gyro-viscosity. Finally, a compact derivation and physical interpretation of one of the forms is reviewed. This appendix employs Bohm-normalized units, as does the main text.
The starting point is (76) of Simakov & Catto (Reference Simakov and Catto2003). Taking the limit of a straight constant
![]() $B$
-field, neglecting parallel flow, parallel gradients and the parallel viscous stress, the vorticity equation given therein may be easily cast into the form
$B$
-field, neglecting parallel flow, parallel gradients and the parallel viscous stress, the vorticity equation given therein may be easily cast into the form
where
![]() ${\it\varpi}=\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{f}=\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(n\boldsymbol{{\rm\nabla}}{\it\Phi}+\boldsymbol{{\rm\nabla}}p_{i})$
, and as in the main text,
${\it\varpi}=\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{f}=\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(n\boldsymbol{{\rm\nabla}}{\it\Phi}+\boldsymbol{{\rm\nabla}}p_{i})$
, and as in the main text,
![]() $\boldsymbol{v}=\boldsymbol{b}\times \boldsymbol{{\rm\nabla}}{\it\Phi}$
. Here
$\boldsymbol{v}=\boldsymbol{b}\times \boldsymbol{{\rm\nabla}}{\it\Phi}$
. Here
and
![]() $n\boldsymbol{v}_{di}=\boldsymbol{b}\times \boldsymbol{{\rm\nabla}}p_{i}$
. Here, and henceforth in this appendix, the operator
$n\boldsymbol{v}_{di}=\boldsymbol{b}\times \boldsymbol{{\rm\nabla}}p_{i}$
. Here, and henceforth in this appendix, the operator
![]() $\boldsymbol{{\rm\nabla}}$
implies
$\boldsymbol{{\rm\nabla}}$
implies
![]() $\boldsymbol{{\rm\nabla}}_{\bot }$
because we focus on the perpendicular gyro-viscous ion physics. In obtaining (A 2) we have employed
$\boldsymbol{{\rm\nabla}}_{\bot }$
because we focus on the perpendicular gyro-viscous ion physics. In obtaining (A 2) we have employed
![]() $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(\boldsymbol{v}{\it\varpi})=\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\varpi}$
. The fact that
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(\boldsymbol{v}{\it\varpi})=\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\varpi}$
. The fact that
![]() $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0$
is used frequently throughout the appendix to move
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0$
is used frequently throughout the appendix to move
![]() $\boldsymbol{v}$
in and outside of the divergence operator.
$\boldsymbol{v}$
in and outside of the divergence operator.
In the following we derive two other equivalent forms for
![]() ${\it\Theta}$
${\it\Theta}$
and
where
![]() $\boldsymbol{f}=n\boldsymbol{{\rm\nabla}}{\it\Phi}+\boldsymbol{{\rm\nabla}}p_{i}$
and the final form of (A 4) employs Cartesian tensor notation with implicit sums on repeated indices. Thus our double-dot convention for index summation is
$\boldsymbol{f}=n\boldsymbol{{\rm\nabla}}{\it\Phi}+\boldsymbol{{\rm\nabla}}p_{i}$
and the final form of (A 4) employs Cartesian tensor notation with implicit sums on repeated indices. Thus our double-dot convention for index summation is
and the dyad operator convention is that
![]() $\boldsymbol{{\rm\nabla}}$
only operates on the quantity to its immediate right. Equation (A 3) is the form given in Umansky et al. (Reference Umansky, Xu, Dudson, LoDestro and Myra2009) and Russell et al. (Reference Russell, D’Ippolito, Myra, Canik, Gray and Zweben2015) while (A 4) is the form used in (2.1).
$\boldsymbol{{\rm\nabla}}$
only operates on the quantity to its immediate right. Equation (A 3) is the form given in Umansky et al. (Reference Umansky, Xu, Dudson, LoDestro and Myra2009) and Russell et al. (Reference Russell, D’Ippolito, Myra, Canik, Gray and Zweben2015) while (A 4) is the form used in (2.1).
From (A 2) we first derive (A 3). Expanding
![]() $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }({\it\varpi}\boldsymbol{v})=\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}(n{\rm\nabla}^{2}{\it\Phi}+\boldsymbol{{\rm\nabla}}n\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\Phi})+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\rm\nabla}^{2}p_{i}$
and starting with the terms that don’t contain
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }({\it\varpi}\boldsymbol{v})=\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}(n{\rm\nabla}^{2}{\it\Phi}+\boldsymbol{{\rm\nabla}}n\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\Phi})+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\rm\nabla}^{2}p_{i}$
and starting with the terms that don’t contain
![]() $p_{i}$
there is a cancellation involving two
$p_{i}$
there is a cancellation involving two
![]() $n{\rm\nabla}^{2}{\it\Phi}$
terms leaving
$n{\rm\nabla}^{2}{\it\Phi}$
terms leaving
Noting that
and applying the vector identity for
![]() $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(\boldsymbol{A}\times \boldsymbol{B})$
to (A 6) one obtains
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(\boldsymbol{A}\times \boldsymbol{B})$
to (A 6) one obtains
Next for the terms involving
![]() $p_{i}$
we have from (A 2) the contribution
$p_{i}$
we have from (A 2) the contribution
Noting that
![]() $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(n\boldsymbol{v}_{di})=0$
and also pulling
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }(n\boldsymbol{v}_{di})=0$
and also pulling
![]() $\boldsymbol{v}$
through the divergence yields
$\boldsymbol{v}$
through the divergence yields
Combining to get
![]() ${\it\Theta}={\it\Theta}^{(1)}+{\it\Theta}^{(2)}$
proves the equivalence of (A 2) and (A 3).
${\it\Theta}={\it\Theta}^{(1)}+{\it\Theta}^{(2)}$
proves the equivalence of (A 2) and (A 3).
To show that (A 3) and (A 4) are equivalent we again begin with the terms that are independent of
![]() $p_{i}$
. Equation (A 4) has the term
$p_{i}$
. Equation (A 4) has the term
Applying the dyad identities
![]() $\boldsymbol{A}\boldsymbol{b}\times \boldsymbol{B}\boldsymbol{ : }\boldsymbol{C}\boldsymbol{D}=-\boldsymbol{A}\boldsymbol{B}\boldsymbol{ : }\boldsymbol{b}\times \boldsymbol{C}\boldsymbol{D}$
and
$\boldsymbol{A}\boldsymbol{b}\times \boldsymbol{B}\boldsymbol{ : }\boldsymbol{C}\boldsymbol{D}=-\boldsymbol{A}\boldsymbol{B}\boldsymbol{ : }\boldsymbol{b}\times \boldsymbol{C}\boldsymbol{D}$
and
![]() $\boldsymbol{A}\boldsymbol{B}\boldsymbol{ : }\boldsymbol{C}\boldsymbol{D}=\boldsymbol{D}\boldsymbol{C}\boldsymbol{ : }\boldsymbol{B}\boldsymbol{A}$
to the first term on the right-hand side of (A 11) we have,
$\boldsymbol{A}\boldsymbol{B}\boldsymbol{ : }\boldsymbol{C}\boldsymbol{D}=\boldsymbol{D}\boldsymbol{C}\boldsymbol{ : }\boldsymbol{B}\boldsymbol{A}$
to the first term on the right-hand side of (A 11) we have,
![]() $\boldsymbol{{\rm\nabla}}(\boldsymbol{b}\times \boldsymbol{{\rm\nabla}}{\it\Phi})\boldsymbol{ : }\boldsymbol{{\rm\nabla}}\boldsymbol{{\rm\nabla}}{\it\Phi}=-\boldsymbol{{\rm\nabla}}\boldsymbol{{\rm\nabla}}{\it\Phi}\boldsymbol{ : }(\boldsymbol{b}\times \boldsymbol{{\rm\nabla}})\boldsymbol{{\rm\nabla}}{\it\Phi}=-\boldsymbol{{\rm\nabla}}(\boldsymbol{b}\times \boldsymbol{{\rm\nabla}}{\it\Phi})\boldsymbol{ : }\boldsymbol{{\rm\nabla}}\boldsymbol{{\rm\nabla}}{\it\Phi}$
, i.e. this term equals its negative and hence vanishes. For the second term we have
$\boldsymbol{{\rm\nabla}}(\boldsymbol{b}\times \boldsymbol{{\rm\nabla}}{\it\Phi})\boldsymbol{ : }\boldsymbol{{\rm\nabla}}\boldsymbol{{\rm\nabla}}{\it\Phi}=-\boldsymbol{{\rm\nabla}}\boldsymbol{{\rm\nabla}}{\it\Phi}\boldsymbol{ : }(\boldsymbol{b}\times \boldsymbol{{\rm\nabla}})\boldsymbol{{\rm\nabla}}{\it\Phi}=-\boldsymbol{{\rm\nabla}}(\boldsymbol{b}\times \boldsymbol{{\rm\nabla}}{\it\Phi})\boldsymbol{ : }\boldsymbol{{\rm\nabla}}\boldsymbol{{\rm\nabla}}{\it\Phi}$
, i.e. this term equals its negative and hence vanishes. For the second term we have
Using
![]() $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0$
, it is not difficult to show that
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0$
, it is not difficult to show that
(An inelegant proof is easily obtained by writing out the components in Cartesian coordinates.) Applying this to (A 12) and employing the result in (A 11) yields the desired result
For the ion pressure terms, it is easiest to start with the terms given in (A 3) and work towards (A 4).
Consider first
A cancellation then occurs in (A 15) which becomes
Employing
![]() ${\rm\nabla}^{2}\boldsymbol{v}=\boldsymbol{b}\times \boldsymbol{{\rm\nabla}}{\rm\nabla}^{2}{\it\Phi}$
one finds immediately that the first and last terms in (A 17) cancel leaving
${\rm\nabla}^{2}\boldsymbol{v}=\boldsymbol{b}\times \boldsymbol{{\rm\nabla}}{\rm\nabla}^{2}{\it\Phi}$
one finds immediately that the first and last terms in (A 17) cancel leaving
which is the desired result. This completes the proof of the equivalence of (A 2)–(A 4).
Finally, the derivation of the ion pressure contributions to the vorticity equation is reviewed from the point of view of the vector ion momentum equation. We make the ansatz that the ion pressure contributions are contained in the terms
where
![]() $\boldsymbol{g}=n\boldsymbol{u}$
and
$\boldsymbol{g}=n\boldsymbol{u}$
and
![]() $\boldsymbol{u}=\boldsymbol{v}+\boldsymbol{v}_{di}$
is the total fluid velocity. The vorticity equation can be derived by applying
$\boldsymbol{u}=\boldsymbol{v}+\boldsymbol{v}_{di}$
is the total fluid velocity. The vorticity equation can be derived by applying
![]() $\boldsymbol{b}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times$
to (A 19). It is useful to note the vector identity for any vector
$\boldsymbol{b}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times$
to (A 19). It is useful to note the vector identity for any vector
![]() $\boldsymbol{A}$
(again with
$\boldsymbol{A}$
(again with
![]() $\boldsymbol{b}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{A}=0$
or
$\boldsymbol{b}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{A}=0$
or
![]() $\boldsymbol{{\rm\nabla}}=\boldsymbol{{\rm\nabla}}_{\bot }$
)
$\boldsymbol{{\rm\nabla}}=\boldsymbol{{\rm\nabla}}_{\bot }$
)
Employing
![]() $\boldsymbol{g}=\boldsymbol{b}\times \boldsymbol{f}$
and using the preceding identity one finds
$\boldsymbol{g}=\boldsymbol{b}\times \boldsymbol{f}$
and using the preceding identity one finds
For the divergence term in (A 19) we apply the same identity with
![]() $\boldsymbol{A}=(\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})\boldsymbol{f}$
. This yields
$\boldsymbol{A}=(\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}})\boldsymbol{f}$
. This yields
Collecting terms we have the vorticity equation in the form of (A 1) and (A 4). This compact derivation recovers the well-known gyro-viscous cancellation: the net effect is that the total fluid momentum
![]() $\boldsymbol{g}$
in (A 19) is only advected by
$\boldsymbol{g}$
in (A 19) is only advected by
![]() $\boldsymbol{v}$
, the
$\boldsymbol{v}$
, the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
part of the total fluid velocity. This is the entire physical content of the complicated terms in (A 2), (A 3) or (A 4).
$\boldsymbol{E}\times \boldsymbol{B}$
part of the total fluid velocity. This is the entire physical content of the complicated terms in (A 2), (A 3) or (A 4).