Hostname: page-component-76fb5796d-vvkck Total loading time: 0 Render date: 2024-04-27T01:22:06.942Z Has data issue: false hasContentIssue false
  • English
  • Français

Are planetary dynamos driven by helical waves?

Part of: 50 years of Mean Field Electrodynamics

Published online by Cambridge University Press:  01 June 2018

P. A. Davidson  and
A. Ranjan
P. A. Davidson*
Affiliation:
Department of Engineering, University of Cambridge, CB21PZ, UK
A. Ranjan
Affiliation:
Department of Engineering, University of Cambridge, CB21PZ, UK
*
†Email address for correspondence: pad3@eng.cam.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

In most numerical simulations of the Earth’s core the dynamo is located outside the tangent cylinder and, in a zero-order sense, takes the form of a classical 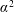$\unicode[STIX]{x1D6FC}^{2}$ dynamo. Such a dynamo usually requires a distribution of helicity, 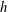$h$, which is asymmetric about the equator and in the simulations it is observed that, outside the tangent cylinder, the helicity is predominantly negative in the north and positive in the south. If we are to extrapolate the results of these simulations to the planets, we must understand how this asymmetry in helicity is established and ask if the same mechanism is likely to operate in a planet. In some of the early numerical dynamos, which were too viscous by a factor of at least 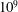$10^{9}$, as measured by the Ekman number, the asymmetric helicity distribution was attributed to Ekman pumping. However, Ekman pumping plays much less of a role in more recent, and less viscous, numerical dynamos, and almost certainly plays no significant role in the core of a planet. So the question remains: what establishes the asymmetric helicity distribution in the simulations and is this mechanism likely to carry over to planetary cores? In this paper we review the evidence that planetary dynamos, and their numerical analogues, might be maintained by helical waves, especially inertial waves, excited in and around the equatorial regions. This cartoon arises from the observation that there tends to be a statistical bias in the buoyancy flux towards the equatorial regions, and so waves are preferentially excited there. Moreover, upward (downward) propagating inertial waves carry negative (positive) helicity, which leads naturally to a segregation in 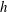$h$.

Keywords

astrophysical plasmas
Type
Review
Information
Journal of Plasma Physics , Volume 84 , Issue 3 , June 2018 , 735840304
Copyright
© Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bardsley, O. P. & Davidson, P. A. 2016 Inertial-Alfven waves as columnar helices in planetary cores. J. Fluid Mech. (Rapids) 805.Google Scholar
Bardsley, O. P. & Davidson, P. A. 2017 The dispersion of magnetic-Coriolis waves in planetary cores. Geophys. J. Intl 210 (1), 18–26.Google Scholar
Bin Baqui, Y. & Davidson, P. A. 2015 A phenomenological theory of rotating turbulence. Phys. Fluids 27 (2), 025107.Google Scholar
Christensen, U. R. 2010 Dynamo scaling laws and application to the planets. Space Sci. Rev. 152, 565–590.CrossRefGoogle Scholar
Christensen, U. R. 2011 Geodynamo models: tools for understanding properties of Earth’s magnetic field. Phys. Earth Planet. Inter. 187, 157–169.CrossRefGoogle Scholar
Christensen, U. R. & Aubert, J. 2006 Scaling properties of convection-driven dynamos in rotating spherical shells and applications to planetary magnetic fields. Geophys. J. Intl 166, 97–114.CrossRefGoogle Scholar
Christensen, U. R., Holzwarth, V. & Reiners, A. 2009 Energy flux determines magnetic field strength of planets and stars. Nature 457, 167–169.Google Scholar
Christensen, U. R. & Wicht, J. 2007 Numerical dynamo simulations. In Treatise on Geophysics (ed. Olson, P.). Elsevier.Google Scholar
Cowling, T. G. 1957 Magnetohydrodynamics. Interscience Publishers.Google Scholar
Davidson, P. A. 2013a Turbulence in Rotating, Stratified and Electrically Conducting Fluids. Cambridge University Press.Google Scholar
Davidson, P. A. 2013b Scaling laws of planetary dynamos. Geophys. J. Intl 195 (1), 67–74.CrossRefGoogle Scholar
Davidson, P. A. 2014 The dynamics and scaling laws of planetary dynamos driven by inertial waves. Geophys. J. Intl 198 (3), 1832–1847.Google Scholar
Davidson, P. A. 2016 Dynamos driven by helical waves: scaling laws for numerical dynamos and for the planets. Geophys. J. Intl 207 (2), 680–690.CrossRefGoogle Scholar
Davidson, P. A. 2017 An Introduction to Magnetohydrodynamics, 2nd edn. Cambridge University Press.Google Scholar
Davidson, P. A. & Ranjan, A. 2015 Planetary dynamos driven by helical waves: Part 2. Geophys. J. Intl 202, 1646–1662.CrossRefGoogle Scholar
Davidson, P. A. & Ranjan, A. 2018 On the spatial segregation of helicity by inertial waves in dynamo simulations and planetary cores. J. Fluid Mech. (to appear).Google Scholar
Davidson, P. A., Staplehurst, P. J. & Dalziel, S. B. 2006 On the evolution of eddies in a rapidly rotating system. J. Fluid Mech. 557, 135–144.Google Scholar
Dickenson, S. C. & Long, R. R. 1983 Oscillating-grid turbulence including effects of rotation. J. Fluid Mech. 126, 315–333.Google Scholar
Glatzmaier, G. A. & Olson, P. 1993 Highly supercritical thermal convection in a rotating spherical shell: centrifugal vs. radial gravity. Geophys. Astrophys. Fluid Dyn. 70 (1–4), 113–136.Google Scholar
Greenspan, H. P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Gubbins, D. 2001 The Rayleigh number for convection in the Earth’s core. Phys. Earth Planet. Inter. 128, 3–12.Google Scholar
Hopfinger, E. J., Browand, F. K. & Gagne, Y. 1982 Turbulence and waves in a rotating tank. J. Fluid Mech. 125, 505–534.Google Scholar
Ibbetson, A. & Tritton, D. J. 1975 Experiments on turbulence in a rotating fluid. J. Fluid Mech. 68 (4), 639–672.Google Scholar
Jones, C. A. 2011 Planetary magnetic fields and fluid dynamos. Annu. Rev. Fluid Mech. 43, 583–614.Google Scholar
King, E. M. & Buffett, B. A. 2013 Flow speeds and length scales in geodynamo models: the role of viscosity. Earth Planet. Sci. Lett. 371–372, 156–162.CrossRefGoogle Scholar
Kono, M., Sakuraba, A. & Ishida, M. 2000 Dynamo simulation and palaeosecular variation models. Phil. Trans. R. Soc. Lond. A 358, 1123–1139.CrossRefGoogle Scholar
Loper, D. E. 2001 On the structure of a Taylor column driven by a buoyant parcel in an unbounded rotating fluid. J. Fluid Mech. 427, 131–165.Google Scholar
Maxworthy, T. 1970 The flow generated by a sphere moving along the axis of a rotating, viscous fluid. J. Fluid Mech. 40 (3), 453–479.CrossRefGoogle Scholar
Moffatt, H. K. 1970 Dynamo action associated with random inertial waves in a rotating conducting fluid. J. Fluid Mech. 44 (4), 705–720.CrossRefGoogle Scholar
Moffatt, H. K. 1978 Magnetic Field Generation in Electrically Conducting Fluids. Cambridge University Press.Google Scholar
Morize, C. & Moisy, F. 2006 Energy decay of rotating turbulence with confinement effects. Phys. Fluids 18, 065107.Google Scholar
Morize, C., Moisy, F. & Rabaud, M. 2005 Decaying grid-generated turbulence in a rotating tank. Phys. Fluids 17, 095105.Google Scholar
Olson, P. 1981 A simple physical model for the terrestrial dynamo. J. Geophys. Res. 86, 10875.Google Scholar
Olson, P., Christensen, U. R. & Glatzmaier, G. A. 1999 Numerical modelling of the geodynamo: mechanisms of field generation and equilibration. J. Geophys. Res. 104 (B5), 10383.Google Scholar
Parker, E. N. 1955 Hydromagnetic dynamo models. Astrophys. J. 122, 293–314.Google Scholar
Pouquet, A. & Mininni, P. D. 2012 The interplay between helicity and rotation in turbulence: implications for scaling laws and small-scale dynamics. Phil. Trans. R. Soc. A 368, 1635–1662.Google Scholar
Ranjan, A. & Davidson, P. A. 2014 Evolution of a turbulent cloud under rotation. J. Fluid Mech. 756, 488–509.CrossRefGoogle Scholar
Ranjan, A., Davidson, P. A., Christensen, U. R. & Wicht, J. 2018 Internally-driven inertial waves in geodynamo simulations. Geophys. J. Intl 213 (2), 1281–1295.Google Scholar
Roberts, P. H. & King, E. M. 2013 On the genesis of the Earth’s magnetism. Rep. Prog. Phys. 76 (9), 096801.Google Scholar
Read, P. L. et al. 2015 Global energy budgets and ‘Trenberth diagrams’ for the climates of terrestrial and gas giant planets. Q. J. R. Meteorol. Soc. 142, 703–720.Google Scholar
Sakuraba, A. & Roberts, P. H. 2009 Generation of a strong magnetic field using uniform heat flux at the surface of the core. Nat. Geosci. 2, 802–805.Google Scholar
Sakuraba, A. & Roberts, P. H. 2011 On thermal driving of the geodynamo. In The Earth’s Magnetic Interior, pp. 117–129. Springer.CrossRefGoogle Scholar
Schaeffer, N., Jault, D., Nataf, H.-C. & Fournier, A. 2017 Turbulent geodynamo simulations: a leap towards Earth’s core. Geophys. J. Intl 211, 1–29.Google Scholar
Sheyko, A.2014 Numerical investigations of rotating MHD in a spherical shell. PhD thesis, ETH-Zurich.Google Scholar
Sreenivasan, B. & Davidson, P. A. 2008 On the formation of cyclones and anticyclones in a rotating fluid. Phys. Fluids 20 (8), 085104.Google Scholar
Staplehurst, P. J., Davidson, P. A. & Dalziel, S. B. 2008 J. Fluid Mech. 598, 81–105.CrossRefGoogle Scholar
Steenbeck, M., Krause, F. & Radler, K.-H. 1966 A calculation of the mean electromotive force in an electrically conducting fluid in turbulent motion, under the influence of Coriolis forces. Z. Naturforsch. 21a, 369–376.Google Scholar
Stellmach, S. & Hansen, U. 2004 Cartesian convection driven dynamos at low Ekman number. Phys. Rev. E 70 (5), 056312.Google Scholar
Thiele, M. & Muller, W.-C. 2009 Structure and decay of rotating homogeneous turbulence. J. Fluid Mech. 637, 425–442.Google Scholar
Wang, Y.-X., Lu, X.-Y. & Zhuang, L.-X. 2004 Numerical analysis of the rotating viscous flow approaching a solid sphere. Intl J. Numer. Methods Fluids 44, 905–925.CrossRefGoogle Scholar
Wigeland, R. A. & Nagib, H. M. 1978 Grid generated turbulence with and without rotation about the streamwise direction. IIT Fluid Heat Transfer Rep. R. 78-1.Google Scholar
Yadav, R. K., Gastine, T. & Christensen, U. R. 2013 Scaling laws in spherical shell dynamos with free-slip boundaries. Icarus 225, 184.Google Scholar