Hostname: page-component-7dd5485656-wjfd9 Total loading time: 0 Render date: 2025-10-31T03:17:38.108Z Has data issue: false hasContentIssue false
  • English
  • Français

Counter differential rigid-rotation equilibrium of electrically non-neutral two-fluid plasma with finite pressure

Published online by Cambridge University Press:  31 August 2021

Y. Nakajima Open the ORCID record for Y. Nakajima [Opens in a new window] ,
H. Himura Open the ORCID record for H. Himura [Opens in a new window]  and
A. Sanpei
Y. Nakajima*
Affiliation:
Department of Electronics, Kyoto Institute of Technology, Matsugasaki, Sakyo Ward, Kyoto 606-8585, Japan
H. Himura*
Affiliation:
Department of Electronics, Kyoto Institute of Technology, Matsugasaki, Sakyo Ward, Kyoto 606-8585, Japan
A. Sanpei
Affiliation:
Department of Electronics, Kyoto Institute of Technology, Matsugasaki, Sakyo Ward, Kyoto 606-8585, Japan
*
†Email addresses for correspondence: m0621027@edu.kit.ac.jp, himura@kit.ac.jp
†Email addresses for correspondence: m0621027@edu.kit.ac.jp, himura@kit.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

We derive the two-dimensional counter-differential rotation equilibria of two-component plasmas, composed of both ion and electron ($e^-$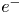) clouds with finite temperatures, for the first time. In the equilibrium found in this study, as the density of the $e^{-}$ 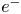cloud is always larger than that of the ion cloud, the entire system is a type of non-neutral plasma. Consequently, a bell-shaped negative potential well is formed in the two-component plasma. The self-electric field is also non-uniform along the $r$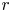-axis. Moreover, the radii of the ion and $e^{-}$ 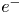plasmas are different. Nonetheless, the pure ion as well as $e^{-}$ 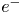plasmas exhibit corresponding rigid rotations around the plasma axis with different fluid velocities, as in a two-fluid plasma. Furthermore, the $e^{-}$ plasma rotates in the same direction as that of $\boldsymbol {E \times B}$, whereas the ion plasma counter-rotates overall. This counter-rotation is attributed to the contribution of the diamagnetic drift of the ion plasma because of its finite pressure.

Keywords

strongly coupled plasmasplasma dynamicsplasma confinement

Information

Type
Research Article
Information
Journal of Plasma Physics , Volume 87 , Issue 4 , August 2021 , 905870415
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

Akaike, K. & Himura, H. 2018 Studies of ion leakage from a penning trap induced by potential barrier closure. Phys. Plasmas 25 (12), 122108.CrossRefGoogle Scholar
Akaike, K. & Himura, H. 2019 A method for avoiding following ion leakage from a penning trap. Plasma Fusion Res. 14, 4401149–4401149.CrossRefGoogle Scholar
Balbus, S.A., Bonart, J., Latter, H.N. & Weiss, N.O. 2009 Differential rotation and convection in the Sun. Mon. Not. R. Astron. Soc. 400 (1), 176–182.CrossRefGoogle Scholar
Bellan, P.M. 2008 Fundamentals of Plasma Physics. Cambridge University Press.Google Scholar
Berkery, J.W., Pedersen, T.S., Kremer, J.P., Marksteiner, Q.R., Lefrancois, R.G., Hahn, M.S. & Brenner, P.W. 2007 Confinement of pure electron plasmas in the Columbia non-neutral torus. Phys. Plasmas 14 (6), 062503.CrossRefGoogle Scholar
Bollinger, J.J., Wineland, D.J. & Dubin, D.H. E. 1994 Non-neutral ion plasmas and crystals, laser cooling, and atomic clocks. Phys. Plasmas 1 (5), 1403–1414.CrossRefGoogle Scholar
Danielson, J.R., Dubin, D.H.E., Greaves, R.G. & Surko, C.M. 2015 Plasma and trap-based techniques for science with positrons. Rev. Mod. Phys. 87 (1), 247.CrossRefGoogle Scholar
Davidson, R.C. 2001 Physics of Nonneutral Plasmas. World Scientific Publishing Company.CrossRefGoogle Scholar
Davidson, R.C., Chan, H.-W., Chen, C. & Lund, S. 1991 Equilibrium and stability properties of intense non-neutral electron flow. Rev. Mod. Phys. 63 (2), 341.CrossRefGoogle Scholar
Davidson, R.C. & Krall, N.A. 1969 Vlasov description of an electron gas in a magnetic field. Phys. Rev. Lett. 22 (16), 833.CrossRefGoogle Scholar
Davidson, R.C. & Uhm, H.-S. 1978 Influence of finite ion larmor radius effects on the ion resonance instability in a nonneutral plasma column. Phys. Fluids 21 (1), 60–71.CrossRefGoogle Scholar
De Jonghe, J. & Keppens, R. 2020 A two-fluid analysis of waves in a warm ion–electron plasma. Phys. Plasmas 27 (12), 122107.CrossRefGoogle Scholar
Dimonte, G. 1981 Ion Langmuir waves in a nonneutral plasma. Phys. Rev. Lett. 46 (1), 26.CrossRefGoogle Scholar
Dubin, D.H.E. 2020 Normal modes, rotational inertia, and thermal fluctuations of trapped ion crystals. Phys. Plasmas 27 (10), 102107.CrossRefGoogle Scholar
Espinoza-Lozano, B.F.I., Calderón, F.A. & Velazquez, L. 2020 A pure non-neutral plasma under an external harmonic field: equilibrium thermodynamics and chaos. J. Stat. Mech. Theory Exp. 2020 (4), 043205.CrossRefGoogle Scholar
Fajans, J. & Surko, C.M. 2020 Plasma and trap-based techniques for science with antimatter. Phys. Plasmas 27 (3), 030601.CrossRefGoogle Scholar
Gilbert, S.J., Dubin, D.H.E., Greaves, R.G. & Surko, C.M. 2001 An electron–positron beam–plasma instability. Phys. Plasmas 8 (11), 4982–4994.CrossRefGoogle Scholar
Higaki, H., Kaga, C., Fukushima, K., Okamoto, H., Nagata, Y., Kanai, Y. & Yamazaki, Y. 2017 Simultaneous confinement of low-energy electrons and positrons in a compact magnetic mirror trap. New J. Phys. 19 (2), 023016.CrossRefGoogle Scholar
Himura, H. 2016 BX-U linear trap for one-way production and confinement of Li+ and e- plasmas. Nucl. Instrum. Meth. Phys. Res. B 811, 100–107.CrossRefGoogle Scholar
Himura, H., Nakamura, K., Masamune, S., Isobe, M. & Shimizu, A. 2010 Outward electron orbit extending to inward part of closed helical magnetic surfaces surrounded by shifted negative space potential. Phys. Plasmas 17 (3), 032507.CrossRefGoogle Scholar
Himura, H., Wakabayashi, H., Yamamoto, Y., Isobe, M., Okamura, S., Matsuoka, K., Sanpei, A. & Masamune, S. 2007 Experimental verification of nonconstant potential and density on magnetic surfaces of helical nonneutral plasmas. Phys. Plasmas 14 (2), 022507.CrossRefGoogle Scholar
Ishida, A., Steinhauer, L.C. & Peng, Y.-K. M. 2010 Two-fluid low-collisionality equilibrium model and application to spherical torus plasmas. Phys. Plasmas 17 (12), 122507.CrossRefGoogle Scholar
Ito, A. & Nakajima, N. 2021 Two-fluid and finite Larmor radius effects on high-beta tokamak equilibria with flow in reduced magnetohydrodynamics. Phys. Scr. 96 (3), 035602.CrossRefGoogle Scholar
Kabantsev, A.A., Chim, C.Y., O'Neil, T.M. & Driscoll, C.F. 2014 Diocotron and Kelvin mode damping from a flux through the critical layer. Phys. Rev. Lett. 112 (11), 115003.CrossRefGoogle ScholarPubMed
Kabantsev, A.A., Driscoll, C.F., Hilsabeck, T.J., O'Neil, T.M. & Yu, J.H. 2001 Trapped-particle asymmetry modes in single-species plasmas. Phys. Rev. Lett. 87 (22), 225002.CrossRefGoogle ScholarPubMed
Kanki, T. & Nagata, M. 2019 Computation of two-fluid flowing equilibrium of spherical torus plasma using multi-grid method. Intl J. Appl. Electromagn. Mech. 59 (2), 439–446.CrossRefGoogle Scholar
Kato, T., Himura, H., Sowa, S. & Sanpei, A. 2019 Controlling the diameter of a pure electron plasma to produce an exact two-fluid plasma state in a nested trap. Plasma Fusion Res. 14, 1201039–1201039.CrossRefGoogle Scholar
Khamaru, S., Ganesh, R. & Sengupta, M. 2021 A novel quiescent quasi-steady state of a toroidal electron plasma. Phys. Plasmas 28 (4), 042101.CrossRefGoogle Scholar
Levy, R.H., Daugherty, J.D. & Buneman, O. 1969 Ion resonance instability in grossly nonneutral plasmas. Phys. Fluids 12 (12), 2616–2629.CrossRefGoogle Scholar
Malmberg, J.H. & Driscoll, C.F. 1980 Long-time containment of a pure electron plasma. Phys. Rev. Lett. 44 (10), 654.CrossRefGoogle Scholar
Marksteiner, Q.R., Pedersen, T.S., Berkery, J.W., Hahn, M.S., Mendez, J.M., de Gevigney, B.D. & Himura, H. 2008 Observations of an ion-driven instability in non-neutral plasmas confined on magnetic surfaces. Phys. Rev. Lett. 100 (6), 065002.CrossRefGoogle ScholarPubMed
Mironov, V.L. 2021 Self-consistent hydrodynamic two-fluid model of vortex plasma. Phys. Fluids 33 (3), 037116.CrossRefGoogle Scholar
Morel, B., Giust, R., Ardaneh, K. & Courvoisier, F. 2021 A solver based on pseudo-spectral analytical time-domain method for the two-fluid plasma model. Sci. Rep. 11 (1), 1–10.CrossRefGoogle ScholarPubMed
Pedersen, T.S. & Boozer, A.H. 2002 Confinement of nonneutral plasmas on magnetic surfaces. Phys. Rev. Lett. 88 (20), 205002.CrossRefGoogle ScholarPubMed
Romé, M., Maero, G., Panzeri, N. & Pozzoli, R. 2019 Selective excitation of Kelvin–Helmholtz modes with rotating electric fields. In European Physical Society Conference on Plasma Physics. European Physical Society.Google Scholar
Shumlak, U., Lilly, R., Reddell, N., Sousa, E. & Srinivasan, B. 2011 Advanced physics calculations using a multi-fluid plasma model. Comput. Phys. Commun. 182 (9), 1767–1770.CrossRefGoogle Scholar
Stoneking, M.R., Pedersen, T.S., Helander, P., Chen, H., Hergenhahn, U., Stenson, E.V., Fiksel, G., von der Linden, J., Saitoh, H., Surko, C.M., et al. 2020 A new frontier in laboratory physics: magnetized electron–positron plasmas. J. Plasma Phys. 86 (6), 1–26.CrossRefGoogle Scholar
Viray, M.A., Miller, S.A. & Raithel, G. 2020 Coulomb expansion of a cold non-neutral rubidium plasma. Phys. Rev. A 102 (3), 033303.CrossRefGoogle Scholar
Yamada, S., Himura, H., Kato, T., Okada, S., Sanpei, A. & Masamune, S. 2018 Two-dimensional macroscopic shapes of lithium ion and electron plasmas after elapse of two-fluid plasma state. In AIP Conference Proceedings, vol. 1928, p. 020016. AIP Publishing LLC.CrossRefGoogle Scholar
Yoshida, Z., Saitoh, H., Yano, Y., Mikami, H., Kasaoka, N., Sakamoto, W., Morikawa, J., Furukawa, M. & Mahajan, S.M. 2012 Self-organized confinement by magnetic dipole: recent results from RT-1 and theoretical modeling. Plasma Phys. Control. Fusion 55 (1), 014018.CrossRefGoogle Scholar
Zhang, F., Poedts, S., Lani, A., Kuźma, B. & Murawski, K. 2021 Two-fluid modeling of acoustic wave propagation in gravitationally stratified isothermal media. Astrophys. J. 911 (2), 119.CrossRefGoogle Scholar
Zhu, B., Francisquez, M. & Rogers, B.N. 2017 Global 3D two-fluid simulations of the tokamak edge region: turbulence, transport, profile evolution, and spontaneous $E \times B$ rotation. Phys. Plasmas 24 (5), 055903.CrossRefGoogle Scholar