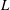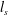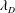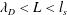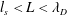1 Introduction
The large mass imbalance between ions and electrons – and the resulting separation of the two types of particles’ length and time scales – is a cornerstone of the physics of traditional plasmas (e.g. Chen Reference Chen1984; Bellan Reference Bellan2006). There are ‘fast’ phenomena that involve electron oscillation (with the ions stationary) and ‘slow’ phenomena that involve ion oscillation (with the electrons reaching equilibrium ‘instantly’ – i.e. on much faster time scales than the motion being considered). In the governing equations, terms with the ratio
![]() $m_{e}/m_{i}$
(electron mass divided by the ion mass) are frequently discarded. Plasma mass density and centre-of-mass velocity are approximated by the ion mass density and centre-of-mass velocity. Intraspecies temperature equilibration is impeded, because, unlike a collision between two equal mass particles (which may transfer up to 100 per cent of one particle’s energy to the other), a collision between particles with a large mass difference transfers comparatively little energy. These are just a few basic examples. More complex plasma phenomena are in turn built on the foundations of mass asymmetry.
$m_{e}/m_{i}$
(electron mass divided by the ion mass) are frequently discarded. Plasma mass density and centre-of-mass velocity are approximated by the ion mass density and centre-of-mass velocity. Intraspecies temperature equilibration is impeded, because, unlike a collision between two equal mass particles (which may transfer up to 100 per cent of one particle’s energy to the other), a collision between particles with a large mass difference transfers comparatively little energy. These are just a few basic examples. More complex plasma phenomena are in turn built on the foundations of mass asymmetry.
Therefore, the concept of a ‘pair plasma’, comprising particles with opposite charge but equal mass, requires all of plasma physics to be revisited from the ground up. Sometimes the end result of the rederivation is no more than an extra factor of 2, as a term that was once negligible compared to its neighbour is now equally important. If, on the other hand, those two terms have opposite signs, they now cancel, fundamentally changing the result. Behaviour can go from linear to nonlinear, be dominated by a different aspect of the physics or disappear entirely. Hundreds of papers have been written on the topic, employing a variety of different theoretical treatments – relativistic and non-relativistic; kinetic and multi-fluid; linear and nonlinear (see, for example, Tsytovich & Wharton Reference Tsytovich and Wharton1978; Stewart & Laing Reference Stewart and Laing1992; Iwamoto Reference Iwamoto1993; Berezhiani & Mahajan Reference Berezhiani and Mahajan1994; Blackman & Field Reference Blackman and Field1994; Zank & Greaves Reference Zank and Greaves1995; Verheest & Lakhina Reference Verheest and Lakhina1996; Mahmood, Mushtaq & Saleem Reference Mahmood, Mushtaq and Saleem2003; Bessho & Bhattacharjee Reference Bessho and Bhattacharjee2005; Gary & Karimabadi Reference Gary and Karimabadi2009; Lopez et al. Reference Lopez, Asenjo, Munoz and Valdivia2012; Helander Reference Helander2014; Liu et al. Reference Liu, Guo, Daughton, Li and Hesse2015; Edwards, Fisch & Mikhailova Reference Edwards, Fisch and Mikhailova2016, just to name a small but diverse selection).
Naturally, interest in creating a pair plasma in the laboratory goes as far back as the first theoretical conceptions of such a thing (Tsytovich & Wharton Reference Tsytovich and Wharton1978). However, this is a significant experimental challenge. It is also one that different researchers around the world approach in a variety of different ways. Progress to date can be summarized as follows:
Pure positron plasma
![]() $+$
electron beam. Two-stream instability seen in a charge neutral system. Electron Debye length exceeded the electron beam diameter (
$+$
electron beam. Two-stream instability seen in a charge neutral system. Electron Debye length exceeded the electron beam diameter (
![]() $\unicode[STIX]{x1D706}_{De}>d_{e}$
) (Greaves & Surko Reference Greaves and Surko1995).
$\unicode[STIX]{x1D706}_{De}>d_{e}$
) (Greaves & Surko Reference Greaves and Surko1995).
Laser-driven, relativistic positron/electron beams. Charge neutrality approached asymptotically, but effectively achieved. Plasma skin depth of the order of or slightly smaller than the beam diameter (
![]() $l_{s}<d$
); simulations predict such a system will exhibit some collective behaviour (Wilks et al.
Reference Wilks, Chen, Liang, Patel, Price, Remington, Shepherd, Tabak and Kruer2005; Chen et al.
Reference Chen, Fiuza, Link, Hazi, Hill, Hoarty, James, Kerr, Meyerhofer and Myatt2015; Liang et al.
Reference Liang, Clarke, Henderson, Fu, Lo, Taylor, Chaguine, Zhou, Hua and Cen2015; Sarri et al.
Reference Sarri, Poder, Cole, Schumaker, Di Piazza, Reville, Dzelzainis, Doria, Gizzi and Grittani2015).
$l_{s}<d$
); simulations predict such a system will exhibit some collective behaviour (Wilks et al.
Reference Wilks, Chen, Liang, Patel, Price, Remington, Shepherd, Tabak and Kruer2005; Chen et al.
Reference Chen, Fiuza, Link, Hazi, Hill, Hoarty, James, Kerr, Meyerhofer and Myatt2015; Liang et al.
Reference Liang, Clarke, Henderson, Fu, Lo, Taylor, Chaguine, Zhou, Hua and Cen2015; Sarri et al.
Reference Sarri, Poder, Cole, Schumaker, Di Piazza, Reville, Dzelzainis, Doria, Gizzi and Grittani2015).
Carbon fullerene pair plasmas. Many Debye lengths achieved. Electrostatic modes investigated. Gyroradius
![]() ${\approx}$
plasma radius (Oohara & Hatakeyama Reference Oohara and Hatakeyama2003; Oohara, Date & Hatakeyama Reference Oohara, Date and Hatakeyama2005; Kono, Vranjes & Batool Reference Kono, Vranjes and Batool2014).
${\approx}$
plasma radius (Oohara & Hatakeyama Reference Oohara and Hatakeyama2003; Oohara, Date & Hatakeyama Reference Oohara, Date and Hatakeyama2005; Kono, Vranjes & Batool Reference Kono, Vranjes and Batool2014).
Low-temperature electrons/positrons in a dipole magnetic field. Only single-species experiments to date (i.e. highly non-neutral). Many Debye lengths achieved with electrons but not yet with positrons. Target is ten Debye lengths for both species in the same system (Saitoh et al. Reference Saitoh, Yoshida, Morikawa, Yano, Hayashi, Mizushima, Kawai, Kobayashi and Mikami2010, Reference Saitoh, Stanja, Stenson, Hergenhahn, Niemann, Pedersen, Stoneking, Piochacz and Hugenschmidt2015; Pedersen et al. Reference Pedersen, Danielson, Hugenschmidt, Marx, Sarasola, Schauer, Schweikhard, Surko and Winkler2012; Stenson et al. Reference Stenson, Saitoh, Stanja, Niemann, Hergenhahn, Pedersen, Marx, Schweikhard, Danielson and Surko2015).
As may be gathered from the above overview, different experimental groups have tended to focus on one of two different parameters as their figure of merit (typically preferring the smaller of the two): plasma skin depth
![]() $l_{s}$
or Debye length
$l_{s}$
or Debye length
![]() $\unicode[STIX]{x1D706}_{D}$
. While the Debye length is often used in textbooks as part of the definition of a plasma, it is also true that traditional laboratory plasmas have very small plasma skin depths, a feature that cannot be taken for granted in very low-density systems.
$\unicode[STIX]{x1D706}_{D}$
. While the Debye length is often used in textbooks as part of the definition of a plasma, it is also true that traditional laboratory plasmas have very small plasma skin depths, a feature that cannot be taken for granted in very low-density systems.
In this paper, we review the physical relevance of each parameter. We discuss how small Debye length does not guarantee small plasma skin depth for plasmas that are thermally non-relativistic, while Debye length can equal or modestly exceed plasma skin depth for plasmas that are thermally relativistic. We note that certain collective interactions can occur before either multiple plasma skin depths or multiple Debye lengths are reached, and we consider the topic of experimental observables for different regimes. While particularly relevant to ongoing pair plasma creation experiments, the transition from single-particle behaviour to collective, ‘plasma’ effects – and how that threshold depends on the phenomena of interest – applies to electron/ion systems as well, but it is often given only a cursory treatment in plasma physics texts and courses. Therefore we will keep the discussion as general as possible, addressing plasmas both with and without a large mass asymmetry and noting differences between the two as they come up.
2 Plasma skin depth and plasma frequency
The plasma skin depth is the depth in a collisionless plasma to which low-frequency electromagnetic radiation can penetrate (as defined by attenuation of the wave amplitude by a factor of
![]() $1/e$
).Footnote
1
Some representative values are listed in table 1. In a traditional plasma, the expression for plasma skin depth is given by
$1/e$
).Footnote
1
Some representative values are listed in table 1. In a traditional plasma, the expression for plasma skin depth is given by
![]() $l_{s}=c/\unicode[STIX]{x1D714}_{pe}$
, where
$l_{s}=c/\unicode[STIX]{x1D714}_{pe}$
, where
![]() $c$
is the speed of light in vacuum. The electron plasma frequency
$c$
is the speed of light in vacuum. The electron plasma frequency
![]() $\unicode[STIX]{x1D714}_{pe}$
is the characteristic frequency for oscillations of the electron density in the ‘cold electron’ limit (i.e. neglecting the effects of thermal motion); it is given by
$\unicode[STIX]{x1D714}_{pe}$
is the characteristic frequency for oscillations of the electron density in the ‘cold electron’ limit (i.e. neglecting the effects of thermal motion); it is given by
![]() $\unicode[STIX]{x1D714}_{pe}=\sqrt{n_{e}e^{2}/(\unicode[STIX]{x1D716}_{0}m_{e})}$
, where
$\unicode[STIX]{x1D714}_{pe}=\sqrt{n_{e}e^{2}/(\unicode[STIX]{x1D716}_{0}m_{e})}$
, where
![]() $n_{e}$
is the number density of the electrons,
$n_{e}$
is the number density of the electrons,
![]() $e$
is the elementary charge,
$e$
is the elementary charge,
![]() $\unicode[STIX]{x1D716}_{0}$
is the permittivity of free space and
$\unicode[STIX]{x1D716}_{0}$
is the permittivity of free space and
![]() $m_{e}$
is the electron mass.
$m_{e}$
is the electron mass.
For electron/positron pair plasmas, a factor of
![]() $\sqrt{2}$
appears, because positrons respond as quickly to density perturbations as electrons do; the picture of a displaced populations of electrons sloshing back and forth past approximately stationary ions does not apply. One option is to redefine
$\sqrt{2}$
appears, because positrons respond as quickly to density perturbations as electrons do; the picture of a displaced populations of electrons sloshing back and forth past approximately stationary ions does not apply. One option is to redefine
![]() $\unicode[STIX]{x1D714}_{pe}$
, replacing
$\unicode[STIX]{x1D714}_{pe}$
, replacing
![]() $m_{e}$
by
$m_{e}$
by
![]() $m_{e}/2$
; another is to leave the definition the same and modify the dispersion relations accordingly (keeping in mind that the definition no longer has the same physical meaning). A hybrid approach is often used in the literature: the definition of
$m_{e}/2$
; another is to leave the definition the same and modify the dispersion relations accordingly (keeping in mind that the definition no longer has the same physical meaning). A hybrid approach is often used in the literature: the definition of
![]() $\unicode[STIX]{x1D714}_{pe}$
is unchanged, but the term ‘plasma frequency’ is used for
$\unicode[STIX]{x1D714}_{pe}$
is unchanged, but the term ‘plasma frequency’ is used for
![]() $\sqrt{2}\unicode[STIX]{x1D714}_{pe}$
. We will use this approach as well, making a point to distinguish between the ‘electron plasma frequency’
$\sqrt{2}\unicode[STIX]{x1D714}_{pe}$
. We will use this approach as well, making a point to distinguish between the ‘electron plasma frequency’
![]() $\unicode[STIX]{x1D714}_{pe}$
and the ‘plasma frequency’
$\unicode[STIX]{x1D714}_{pe}$
and the ‘plasma frequency’
![]() $\unicode[STIX]{x1D714}_{p}$
that represents a fundamental frequency of the system and is given by
$\unicode[STIX]{x1D714}_{p}$
that represents a fundamental frequency of the system and is given by
This yields the expression for pair plasma skin depth
Table 1. Plasma skin depths (
![]() $l_{s}$
) for a range of electron densities (
$l_{s}$
) for a range of electron densities (
![]() $n_{e}$
), as well as the cutoff wavelength for transmission of incident EM waves (
$n_{e}$
), as well as the cutoff wavelength for transmission of incident EM waves (
![]() $\unicode[STIX]{x1D706}_{cutoff}=2\unicode[STIX]{x03C0}\,l_{s}$
), adapted from Attwood (Reference Attwood2009). Except where noted, a non-relativistic electron/ion plasma is assumed.
$\unicode[STIX]{x1D706}_{cutoff}=2\unicode[STIX]{x03C0}\,l_{s}$
), adapted from Attwood (Reference Attwood2009). Except where noted, a non-relativistic electron/ion plasma is assumed.

a As given by Liang et al. (Reference Liang, Clarke, Henderson, Fu, Lo, Taylor, Chaguine, Zhou, Hua and Cen2015) and Sarri et al. (Reference Sarri, Poder, Cole, Schumaker, Di Piazza, Reville, Dzelzainis, Doria, Gizzi and Grittani2015).
In traditional, electron/ion plasmas, the plasma frequency appears in the dispersion relation for all elementary plasma waves in which electrons are oscillating, and it is a cutoff for Langmuir waves, which have the dispersion relation
![]() $\unicode[STIX]{x1D714}^{2}=\unicode[STIX]{x1D714}_{pe}^{2}+3v_{Te}^{2}k^{2}$
, as well as for transverse electromagnetic waves (in unmagnetized plasma) and ordinary waves (in magnetized plasma), both of which have the dispersion relation
$\unicode[STIX]{x1D714}^{2}=\unicode[STIX]{x1D714}_{pe}^{2}+3v_{Te}^{2}k^{2}$
, as well as for transverse electromagnetic waves (in unmagnetized plasma) and ordinary waves (in magnetized plasma), both of which have the dispersion relation
![]() $\unicode[STIX]{x1D714}^{2}=\unicode[STIX]{x1D714}_{pe}^{2}+c^{2}k^{2}$
. (The frequency and wavenumber for an oscillating mode of the plasma are
$\unicode[STIX]{x1D714}^{2}=\unicode[STIX]{x1D714}_{pe}^{2}+c^{2}k^{2}$
. (The frequency and wavenumber for an oscillating mode of the plasma are
![]() $\unicode[STIX]{x1D714}$
and
$\unicode[STIX]{x1D714}$
and
![]() $k$
, and
$k$
, and
![]() $v_{Te}=\sqrt{\unicode[STIX]{x1D705}T_{e}/m_{e}}$
is the electron thermal velocity, where
$v_{Te}=\sqrt{\unicode[STIX]{x1D705}T_{e}/m_{e}}$
is the electron thermal velocity, where
![]() $\unicode[STIX]{x1D705}$
is Boltzmann’s constant and
$\unicode[STIX]{x1D705}$
is Boltzmann’s constant and
![]() $T_{e}$
is the electron temperature.) For example, light with
$T_{e}$
is the electron temperature.) For example, light with
![]() $\unicode[STIX]{x1D714}<\unicode[STIX]{x1D714}_{pe}$
will be fully reflected while light with
$\unicode[STIX]{x1D714}<\unicode[STIX]{x1D714}_{pe}$
will be fully reflected while light with
![]() $\unicode[STIX]{x1D714}>\unicode[STIX]{x1D714}_{pe}$
will be transmitted.
$\unicode[STIX]{x1D714}>\unicode[STIX]{x1D714}_{pe}$
will be transmitted.
In electron/positron pair plasmas, for the reasons outlined previously, the cutoff for Langmuir and light waves is
![]() $\sqrt{2}\unicode[STIX]{x1D714}_{pe}$
. The equations are given by
$\sqrt{2}\unicode[STIX]{x1D714}_{pe}$
. The equations are given by
and
respectively. (Additional differences include there being no distinction between
![]() $L$
and
$L$
and
![]() $R$
waves, acoustic waves being heavily Landau damped, the absence of whistler waves and much more (Tsytovich & Wharton Reference Tsytovich and Wharton1978; Stewart & Laing Reference Stewart and Laing1992; Iwamoto Reference Iwamoto1993; Zank & Greaves Reference Zank and Greaves1995).)
$R$
waves, acoustic waves being heavily Landau damped, the absence of whistler waves and much more (Tsytovich & Wharton Reference Tsytovich and Wharton1978; Stewart & Laing Reference Stewart and Laing1992; Iwamoto Reference Iwamoto1993; Zank & Greaves Reference Zank and Greaves1995).)
Frequency cutoffs are a valuable diagnostic tool in plasma physics, due to their dependence on conditions that one wants to measure (e.g. plasma density). The most basic version of this measurement is to ramp up the frequency of the transmitter until one detects a transmitted wave at the receiver on the far side of the plasma; (2.1) is used to calculate the peak electron density. A more sophisticated system involves sending in a wave with a frequency below the cutoff; looking at when and where it reflects back; calculating where in the plasma the reflection occurred; and repeating this for different frequencies to get a density profile. These techniques fail, however, if the length scale over which reflection occurs (e.g. the skin depth, in the case of light waves) is larger than the system size.
Finally, the plasma skin depth is also the characteristic length scale for the Weibel instability, in which an anisotropic velocity distribution results in current filamentation, leading to magnetic field generation and shock formation. Observation of the Weibel instability is a goal for laser-generated electron/positron experiments (e.g. Chen et al. Reference Chen, Fiuza, Link, Hazi, Hill, Hoarty, James, Kerr, Meyerhofer and Myatt2015).
3 Debye length and quasi-neutrality
The plasma Debye length
![]() $\unicode[STIX]{x1D706}_{D}$
is the characteristic distance over which electrostatic potentials are ‘screened out’ or attenuated by a redistribution of the charged particles. Some representative values are listed in table 2. In vacuum, the electrostatic potential of a particle with charge
$\unicode[STIX]{x1D706}_{D}$
is the characteristic distance over which electrostatic potentials are ‘screened out’ or attenuated by a redistribution of the charged particles. Some representative values are listed in table 2. In vacuum, the electrostatic potential of a particle with charge
![]() $Q$
(i.e. the Coulomb potential) falls off gradually, inversely proportional to the distance
$Q$
(i.e. the Coulomb potential) falls off gradually, inversely proportional to the distance
![]() $r$
from the particle:
$r$
from the particle:
By contrast, the potential due to a charged particle in a plasma falls off faster, as
where the Debye length is defined as
where the sum is over those charge species participating in the screening, and
where
![]() $\unicode[STIX]{x1D70E}$
identifies the charge species and
$\unicode[STIX]{x1D70E}$
identifies the charge species and
![]() $T_{\unicode[STIX]{x1D70E}}$
,
$T_{\unicode[STIX]{x1D70E}}$
,
![]() $n_{\unicode[STIX]{x1D70E}}$
and
$n_{\unicode[STIX]{x1D70E}}$
and
![]() $q_{\unicode[STIX]{x1D70E}}$
are the species temperature, equilibrium density (in the absence of the test charge
$q_{\unicode[STIX]{x1D70E}}$
are the species temperature, equilibrium density (in the absence of the test charge
![]() $Q$
) and charge, respectively. In traditional, electron/ion plasmas, it is often only electrons that participate in the screening (because ions move too slowly), so the ion term in (3.3) is dropped, and the Debye length is given by the electron term only:
$Q$
) and charge, respectively. In traditional, electron/ion plasmas, it is often only electrons that participate in the screening (because ions move too slowly), so the ion term in (3.3) is dropped, and the Debye length is given by the electron term only:
![]() $\unicode[STIX]{x1D706}_{D}=\sqrt{\unicode[STIX]{x1D716}_{0}\unicode[STIX]{x1D705}T_{e}/(n_{e}\text{e}^{2})}$
. In an electron/positron pair plasma, both species participate in the screening, so the Debye length is smaller by a factor of
$\unicode[STIX]{x1D706}_{D}=\sqrt{\unicode[STIX]{x1D716}_{0}\unicode[STIX]{x1D705}T_{e}/(n_{e}\text{e}^{2})}$
. In an electron/positron pair plasma, both species participate in the screening, so the Debye length is smaller by a factor of
![]() $\sqrt{2}$
(just like the plasma skin depth).
$\sqrt{2}$
(just like the plasma skin depth).
Table 2. Debye lengths for a diverse selection of plasma systems, adapted from Bellan (Reference Bellan2006). MCF and ICF stand for magnetic and inertial confinement fusion, respectively. Debye lengths for electron/ion plasmas assume that screening is dominated by electrons.

If the linear dimensions of a plasma are significantly larger than the Debye length, the system is quasi-neutral; non-neutral regions are at most a few times the size of the Debye length. This holds true regardless of whether the source of the potential perturbation is externally generated (like a probe inserted into the plasma, around which a sheath forms), forms spontaneously between regions of plasma with different characteristics (as is the case for double layers), or arises from random thermal fluctuations.
This last case can be shown by considering the (statistically highly unlikely) situation in which thermal fluctuations result in all the electrons in a spherical region of radius
![]() $r_{max}$
simultaneously moving outward with the precise distribution of velocities that results in them coming to rest (due to the electric field generated by the ions left behind) at the surface of that sphere. Thus, all of the initial electron kinetic energy
$r_{max}$
simultaneously moving outward with the precise distribution of velocities that results in them coming to rest (due to the electric field generated by the ions left behind) at the surface of that sphere. Thus, all of the initial electron kinetic energy
![]() $W_{kinetic}$
due to random thermal motions is converted into electrostatic potential energy
$W_{kinetic}$
due to random thermal motions is converted into electrostatic potential energy
![]() $W_{E}$
:
$W_{E}$
:
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle W_{kinetic}=W_{E}\\ \displaystyle \left(\frac{3}{2}n\unicode[STIX]{x1D705}T_{e}\right)\left(\frac{4}{3}\unicode[STIX]{x03C0}r_{max}^{3}\right)=\int _{0}^{r_{max}}\frac{\unicode[STIX]{x1D716}_{0}E_{r}^{2}}{2}4\unicode[STIX]{x03C0}r^{2}\,\text{d}r,\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle W_{kinetic}=W_{E}\\ \displaystyle \left(\frac{3}{2}n\unicode[STIX]{x1D705}T_{e}\right)\left(\frac{4}{3}\unicode[STIX]{x03C0}r_{max}^{3}\right)=\int _{0}^{r_{max}}\frac{\unicode[STIX]{x1D716}_{0}E_{r}^{2}}{2}4\unicode[STIX]{x03C0}r^{2}\,\text{d}r,\end{array}\right\} & & \displaystyle\end{eqnarray}$$
where
![]() $E_{r}(r)$
is the electric field at radius
$E_{r}(r)$
is the electric field at radius
![]() $r$
from the centre of the spherical region. Equation (3.6) gives
$r$
from the centre of the spherical region. Equation (3.6) gives
![]() $r_{max}\simeq 7\unicode[STIX]{x1D706}_{De}$
(Bellan Reference Bellan2006).
$r_{max}\simeq 7\unicode[STIX]{x1D706}_{De}$
(Bellan Reference Bellan2006).
Another way to understand this equating of the kinetic energy in a region of plasma to the energy in the electric field generated by a single-species plasma of the same size and density is as follows: self-generated, collective dynamics requires that the plasma can create electric fields that compete with – and dominate over – kinetic dynamics (i.e. single particle motion). If, in the upper limit of the hypothetical scenario described above, the potential energy that is generated is less than the kinetic energy of the particles, then this cloud cannot generate collective potentials that single particles care about.
In single-component plasmas (which cannot screen potentials with the same sign as that of the particles, since all the particles will move away from the source of the perturbation, leaving only vacuum behind), this relationship between plasma potential and kinetic energy provides the definition for the Debye length (Knoop, Madsen & Thompson Reference Knoop, Madsen and Thompson2016).
Beyond being part of the overall criteria for which ionized gas qualifies as a plasma and which does not, quasi-neutrality (and/or a small Debye length) is incorporated into many (but by no means all) of the equations that describe plasma physics phenomena, as it is a common starting point or simplifying assumption. This is particularly true of low-frequency phenomena; no less than the equation of motion that governs magnetohydrodynamics (MHD), for example, includes the assumption of quasi-neutrality. It also shows up in such places as the Fokker–Planck treatment of plasma collisions, the derivations of ion acoustic waves and their soliton counterparts and the theory of drift waves (Bellan Reference Bellan2006).
One example of particular interest for the magnetic fusion community is the physics of interchange modes, which play a major role in the dynamics of plasmas confined in inhomogeneous magnetic fields, especially in toroidal configurations such as magnetospheres or in magnetic confinement fusion devices. In many cases, interchange dynamics can be understood from the single-particle picture as arising from the fact that the magnetic drifts (
![]() $\unicode[STIX]{x1D735}B$
and curvature drift) are opposite in direction for the positive and negative species, as a result of which a polarization of the plasma appears. This creates an electric field that can overwhelm the magnetic drifts and leads to the plasma
$\unicode[STIX]{x1D735}B$
and curvature drift) are opposite in direction for the positive and negative species, as a result of which a polarization of the plasma appears. This creates an electric field that can overwhelm the magnetic drifts and leads to the plasma
![]() $E\times B$
drifting as a whole. However, since this electric field cannot be larger than what is produced by having the two species drift apart entirely (akin to the hypothetical scenario described previously), this large-scale motion can only occur in systems with a small Debye length compared to the plasma size and radius of curvature (Goldston & Rutherford Reference Goldston and Rutherford1995).
$E\times B$
drifting as a whole. However, since this electric field cannot be larger than what is produced by having the two species drift apart entirely (akin to the hypothetical scenario described previously), this large-scale motion can only occur in systems with a small Debye length compared to the plasma size and radius of curvature (Goldston & Rutherford Reference Goldston and Rutherford1995).
While all of the above phenomena have been mentioned in the context of their derivations for traditional, electron–ion plasmas, they typically also apply to the corresponding theory of pair plasmas, albeit often with different results. As mentioned previously, interspecies collisions in pair plasmas transfer momentum at the same rate as intraspecies collisions, and there is no low-frequency regime in which the heavier species’ behaviour determines the interesting physics while the lighter species is just ‘along for the ride’. Recent papers investigating the nature of the acoustic mode (Edwards et al. Reference Edwards, Fisch and Mikhailova2016) and magnetic confinement stability (Helander Reference Helander2014; Helander & Connor Reference Helander and Connor2016) have pointed out dramatic differences.
4 Relationships between
 $l_{s}$
and
$l_{s}$
and
 $\unicode[STIX]{x1D706}_{D}$
$\unicode[STIX]{x1D706}_{D}$
Both plasma skin depth and Debye length scale with
![]() $1/\sqrt{n_{e}}$
, but whereas skin depth depends only on density, Debye length depends on both density and temperature (figure 1). Combining (2.2) and (2.1) yields an expression for skin depth very similar to (3.5) for the Debye length, except the expression for
$1/\sqrt{n_{e}}$
, but whereas skin depth depends only on density, Debye length depends on both density and temperature (figure 1). Combining (2.2) and (2.1) yields an expression for skin depth very similar to (3.5) for the Debye length, except the expression for
![]() $l_{s}$
has
$l_{s}$
has
![]() $\sqrt{m_{e}c^{2}}$
in the numerator instead of
$\sqrt{m_{e}c^{2}}$
in the numerator instead of
![]() $\sqrt{\unicode[STIX]{x1D705}T_{e}}$
. Thus, which of the two length scales is smaller depends on the relationship between
$\sqrt{\unicode[STIX]{x1D705}T_{e}}$
. Thus, which of the two length scales is smaller depends on the relationship between
![]() $\unicode[STIX]{x1D705}T_{e}$
and
$\unicode[STIX]{x1D705}T_{e}$
and
![]() $m_{e}c^{2}$
:
$m_{e}c^{2}$
:

Figure 1. The ratio
![]() $l_{s}/\unicode[STIX]{x1D706}_{D}$
of the plasma skin depth to the Debye length depends on the plasma temperature. (a) Skin depth and Debye length both scale in inverse proportion to the square root of density. Examples are shown for three plasmas with different electron temperatures (
$l_{s}/\unicode[STIX]{x1D706}_{D}$
of the plasma skin depth to the Debye length depends on the plasma temperature. (a) Skin depth and Debye length both scale in inverse proportion to the square root of density. Examples are shown for three plasmas with different electron temperatures (
![]() $T_{e1}<T_{e2}<T_{e3}$
). Plasmas 1 and 2 are thermally non-relativistic. Plasma 3 is thermally relativistic and has a non-Maxwellian velocity distribution function, resulting in
$T_{e1}<T_{e2}<T_{e3}$
). Plasmas 1 and 2 are thermally non-relativistic. Plasma 3 is thermally relativistic and has a non-Maxwellian velocity distribution function, resulting in
![]() $\unicode[STIX]{x1D706}_{D}>l_{s}$
. (b) Debye length versus skin depth, both normalized to the system size, for plasmas of various temperatures (dotted lines). Changing the system size while keeping the density and temperature constant or changing the density while keeping the system size and temperature constant corresponds to moving along the appropriate isotherm (blue arrow). Increasing the temperature while keeping the density and system size constant increases only the Debye length for non-relativistic plasmas; for relativistic plasmas, the skin depth becomes temperature-dependent via the Lorentz factor (red arrows, with light red indicating an ultra-relativistic Maxwellian and dark red indicating a non-Maxwellian distribution). The standard textbook definition of a plasma is ‘many Debye lengths’ – e.g. 10 (green line).
$\unicode[STIX]{x1D706}_{D}>l_{s}$
. (b) Debye length versus skin depth, both normalized to the system size, for plasmas of various temperatures (dotted lines). Changing the system size while keeping the density and temperature constant or changing the density while keeping the system size and temperature constant corresponds to moving along the appropriate isotherm (blue arrow). Increasing the temperature while keeping the density and system size constant increases only the Debye length for non-relativistic plasmas; for relativistic plasmas, the skin depth becomes temperature-dependent via the Lorentz factor (red arrows, with light red indicating an ultra-relativistic Maxwellian and dark red indicating a non-Maxwellian distribution). The standard textbook definition of a plasma is ‘many Debye lengths’ – e.g. 10 (green line).
For plasmas that are thermally non-relativistic (
![]() $\unicode[STIX]{x1D705}T_{e}\ll m_{e}c^{2}=0.5$
MeV) and have a Maxwellian temperature distribution, as has been assumed up to this point, this ratio simplifies to
$\unicode[STIX]{x1D705}T_{e}\ll m_{e}c^{2}=0.5$
MeV) and have a Maxwellian temperature distribution, as has been assumed up to this point, this ratio simplifies to
![]() $c/v_{Te}$
, and the Debye length is smaller than the skin depth. For example, the ratio
$c/v_{Te}$
, and the Debye length is smaller than the skin depth. For example, the ratio
![]() $l_{s}/\unicode[STIX]{x1D706}_{D}$
is 23 for a 1 keV plasma and 715 for a 1 eV plasma.
$l_{s}/\unicode[STIX]{x1D706}_{D}$
is 23 for a 1 keV plasma and 715 for a 1 eV plasma.
For plasmas that are thermally relativistic (
![]() $\unicode[STIX]{x1D705}T_{e}\gtrsim m_{e}c^{2}$
), the skin depth is subject to a relativistic correction, with
$\unicode[STIX]{x1D705}T_{e}\gtrsim m_{e}c^{2}$
), the skin depth is subject to a relativistic correction, with
![]() $m_{e}\rightarrow \langle \unicode[STIX]{x1D6FE}\rangle \,m_{e}$
where
$m_{e}\rightarrow \langle \unicode[STIX]{x1D6FE}\rangle \,m_{e}$
where
![]() $\langle \unicode[STIX]{x1D6FE}\rangle$
is the average Lorentz factor, while the Debye length is not (Melrose Reference Melrose2008). For an ultra-relativistic Maxwellian velocity distribution,
$\langle \unicode[STIX]{x1D6FE}\rangle$
is the average Lorentz factor, while the Debye length is not (Melrose Reference Melrose2008). For an ultra-relativistic Maxwellian velocity distribution,
![]() $\langle \unicode[STIX]{x1D6FE}\rangle =3\unicode[STIX]{x1D705}T_{e}/(m_{e}c^{2})$
(Wei-Ke et al.
Reference Wei-Ke, Xi-Jun, Chun-Hua and Zhi-Yuan2005), so (4.1) simplifies to
$\langle \unicode[STIX]{x1D6FE}\rangle =3\unicode[STIX]{x1D705}T_{e}/(m_{e}c^{2})$
(Wei-Ke et al.
Reference Wei-Ke, Xi-Jun, Chun-Hua and Zhi-Yuan2005), so (4.1) simplifies to
![]() $l_{s}/\unicode[STIX]{x1D706}_{D}=\sqrt{3}$
. If a distribution is not Maxwellian, the expression for the Debye length (3.5) is modified; whether it is shorter or longer than the Maxwellian case depends on the distribution (Bryant Reference Bryant1996; Hansen, Reimann & Fajans Reference Hansen, Reimann and Fajans1996; Rubab & Murtaza Reference Rubab and Murtaza2006). In the relativistic limit, where the two length scales are comparable, this can lead to the Debye length equalling or modestly exceeding the skin depth.
$l_{s}/\unicode[STIX]{x1D706}_{D}=\sqrt{3}$
. If a distribution is not Maxwellian, the expression for the Debye length (3.5) is modified; whether it is shorter or longer than the Maxwellian case depends on the distribution (Bryant Reference Bryant1996; Hansen, Reimann & Fajans Reference Hansen, Reimann and Fajans1996; Rubab & Murtaza Reference Rubab and Murtaza2006). In the relativistic limit, where the two length scales are comparable, this can lead to the Debye length equalling or modestly exceeding the skin depth.
One can also rearrange (4.1) to emphasize that the inverse plasma frequency is the inertial time scale for the electrons:
Phenomena with time scales faster than the inverse of the plasma frequency will not necessarily maintain quasi-neutrality, because the electrons are far from force balance. Nevertheless, large areas of non-neutrality are not possible, since the plasma itself does not have sufficient energy to do this, as described in the previous section.
5 Magnetization
Magnetization of a plasma introduces additional length and time scales (corresponding to the period and radius of a charged particle’s cyclotron orbit in the magnetic field), in addition to introducing significant anisotropy (parallel versus perpendicular to the magnetic field). Waves in magnetized plasma are significantly different than those in unmagnetized plasma, with the exception of compressional (electrostatic) waves propagating parallel to the magnetic field. Many of the differences between pair plasmas and normal plasmas involve magnetized waves, including one that does not have an electron–ion plasma equivalent (Zank & Greaves Reference Zank and Greaves1995). In the high-frequency limit, this new wave propagates non-dispersively at the acoustic velocity, which in pair plasmas differs from the thermal velocity only by a factor of the adiabatic index
![]() $\unicode[STIX]{x1D6FE}$
, where
$\unicode[STIX]{x1D6FE}$
, where
![]() $\unicode[STIX]{x1D6FE}=1$
–3, depending on how far a process is from meeting the adiabatic criterion (Edwards et al.
Reference Edwards, Fisch and Mikhailova2016).
$\unicode[STIX]{x1D6FE}=1$
–3, depending on how far a process is from meeting the adiabatic criterion (Edwards et al.
Reference Edwards, Fisch and Mikhailova2016).
Nor are all magnetized plasmas alike. Strongly magnetized plasmas exhibit behaviour distinct from weakly magnetized plasmas. This is particularly well illustrated by the CMA (Clemmow–Mullaly–Allis) diagram (figure 2), which depicts the qualitatively different ‘cold’ plasma modes (i.e. those for which the dispersion relation is not temperature dependent) for different plasma densities (horizontal axis) and magnetic fields (vertical axis). A ‘frequency scan’ in a uniform plasma (i.e. with density and magnetic field fixed) corresponds to moving along a diagonal line; not all lines can access all types of plasma waves. Examining the CMA diagram also highlights the interesting physics available at higher frequencies, such as the cyclotron and hybrid frequencies.

Figure 2. CMA diagrams illustrate cutoffs, principle resonances, wave normal surfaces and other properties of the cold plasma dispersion relation for (a) electron–ion plasmas (from Bellan (Reference Bellan2006)) and (b) pair plasmas. As per the standard analysis (e.g. Stix Reference Stix1992), modes are plane waves in an infinite, homogeneous plasma;
![]() $\unicode[STIX]{x1D61A}$
,
$\unicode[STIX]{x1D61A}$
,
![]() $\unicode[STIX]{x1D617}$
and
$\unicode[STIX]{x1D617}$
and
![]() $\unicode[STIX]{x1D60B}$
(not shown) are elements of the dielectric tensor,
$\unicode[STIX]{x1D60B}$
(not shown) are elements of the dielectric tensor,
![]() $\unicode[STIX]{x1D619}=\unicode[STIX]{x1D61A}+\unicode[STIX]{x1D60B}$
, and
$\unicode[STIX]{x1D619}=\unicode[STIX]{x1D61A}+\unicode[STIX]{x1D60B}$
, and
![]() $\unicode[STIX]{x1D613}=\unicode[STIX]{x1D61A}-\unicode[STIX]{x1D60B}$
. Note that for pair plasmas, it is always the case that
$\unicode[STIX]{x1D613}=\unicode[STIX]{x1D61A}-\unicode[STIX]{x1D60B}$
. Note that for pair plasmas, it is always the case that
![]() $\unicode[STIX]{x1D619}=\unicode[STIX]{x1D613}=\unicode[STIX]{x1D61A}$
, so there is at most one mode for waves propagating parallel to the magnetic field; i.e. the two wave normal surfaces always coincide at
$\unicode[STIX]{x1D619}=\unicode[STIX]{x1D613}=\unicode[STIX]{x1D61A}$
, so there is at most one mode for waves propagating parallel to the magnetic field; i.e. the two wave normal surfaces always coincide at
![]() $\unicode[STIX]{x1D703}=0$
.
$\unicode[STIX]{x1D703}=0$
.
In terms of diagnostic accessibility, high-frequency waves ‘fit’ into low-density plasmas if the system size is significantly larger than the Larmor radius
![]() $r_{L}$
, which depends on temperature and magnetic field
$r_{L}$
, which depends on temperature and magnetic field
![]() $B$
as
$B$
as
where
![]() $\unicode[STIX]{x1D714}_{c}=eB/m$
is the cyclotron frequency. Cyclotron resonances are a valuable tool for controlling and diagnosing magnetized plasmas. In addition to the wave physics that can be identified from the CMA diagram, extending one’s sights to ‘warm’ plasma modes (e.g. Bernstein waves, which occur at multiples of the cyclotron frequency) further extends the options.
$\unicode[STIX]{x1D714}_{c}=eB/m$
is the cyclotron frequency. Cyclotron resonances are a valuable tool for controlling and diagnosing magnetized plasmas. In addition to the wave physics that can be identified from the CMA diagram, extending one’s sights to ‘warm’ plasma modes (e.g. Bernstein waves, which occur at multiples of the cyclotron frequency) further extends the options.
Finally, a magnetically confined pair plasma is an ideal environment for testing theories about turbulence, microinstabilities and anomalous transport (all of which are also ‘warm’ plasma effects). In traditional plasmas, these issues are very active areas of research, due to their importance for the ultimate success of fusion energy as well as for the understanding of space and astrophysical plasmas. Turbulence occurs on both ion and electron scales, and coupling between the two types of turbulence is essential for the understanding of magnetic fusion reactor heat loss (Howard et al. Reference Howard, Holland, White, Greenwald and Candy2016). In pair plasmas, not only is this large difference in length scales absent (unless there is a large difference in temperatures between the two species), but gyrokinetic theory predicts that pair plasmas will be stable to the modes that dominate in electron–ion plasmas (Helander Reference Helander2014; Helander & Connor Reference Helander and Connor2016). Being able to verify this prediction and, more generally, to study microstability in pair plasmas would provide an invaluable comparison for traditional plasmas and the tools used to describe/simulate them.
6 Threshold for collective interactions
The presence of collective phenomena does not necessarily mean that one has a plasma in the usual, textbook sense. As a trivial example, the electron gas in a solid experiences plasma oscillations; the plasma state is not required. Additionally, certain collective phenomena can also be observed in a group of charged particles before either multiple Debye lengths or multiple skin depths are achieved in one’s system.
This has long been observed by those who study non-neutral plasmas, which are typically very diffuse (i.e. have very long skin depths) and which not infrequently come into existence via a transition from ‘trapped charge particles’ to ‘plasma’. In pure electron experiments in the levitated dipole Ring-Trap 1, for example, a diocotron-like mode (a collective effect in non-neutral plasmas) was observed even when the Debye length was of the order of the system size or larger (Saitoh et al. Reference Saitoh, Yoshida, Morikawa, Yano, Hayashi, Mizushima, Kawai, Kobayashi and Mikami2010). Interestingly, the ‘rotating wall’ in a Penning trap works both for clouds of ‘trapped charged particles’ and for ‘plasmas’, but via different physical mechanisms (Anderegg, Hollmann & Driscoll Reference Anderegg, Hollmann and Driscoll1998; Greaves & Surko Reference Greaves and Surko2000; Danielson & Surko Reference Danielson and Surko2005).
A prominent example from quasi-neutral plasmas is the two-stream instability. Evidence for this instability, which grows much more quickly for pair plasmas than for electron–ion plasmas, was already seen in the electron beam/positron plasma system investigated by Greaves & Surko (Reference Greaves and Surko1995). Because the instability criterion is given by
![]() $0<ku_{0}/\unicode[STIX]{x1D714}_{pe}<\sqrt{2}$
, where
$0<ku_{0}/\unicode[STIX]{x1D714}_{pe}<\sqrt{2}$
, where
![]() $u_{0}$
is the relative velocity between two oppositely directed streams, smaller
$u_{0}$
is the relative velocity between two oppositely directed streams, smaller
![]() $\unicode[STIX]{x1D714}_{pe}$
(associated with a lower density and a longer skin depth) means that unstable modes simply occur at smaller
$\unicode[STIX]{x1D714}_{pe}$
(associated with a lower density and a longer skin depth) means that unstable modes simply occur at smaller
![]() $u_{0}$
, rather than requiring small
$u_{0}$
, rather than requiring small
![]() $k$
, large-wavelength behaviour that does not ‘fit’ in the system. Interestingly, the derivation for the instability criterion assumes quasi-neutrality, which, as described in the previous section, is not a given for small Debye length systems; in the case of these experiments, the Debye length for the positron plasma was smaller than the radius of the electron beam, but the Debye length for the electrons was not.
$k$
, large-wavelength behaviour that does not ‘fit’ in the system. Interestingly, the derivation for the instability criterion assumes quasi-neutrality, which, as described in the previous section, is not a given for small Debye length systems; in the case of these experiments, the Debye length for the positron plasma was smaller than the radius of the electron beam, but the Debye length for the electrons was not.
Since the two-stream instability is related to the Weibel instability, in that the initial velocity space anisotropy can be thought of as multiple counter-streaming beams (Fried Reference Fried1959), this raises the question of whether it might also be possible to observe evidence of the Weibel instability in pair plasmas at lower densities than are required to fit many skin depths into the system size.
Similarly, recent work has suggested that stimulated Brillouin scattering (a type of three wave coupling) could be used to diagnose pair plasmas (Edwards et al.
Reference Edwards, Fisch and Mikhailova2016). The waves in question are ‘low-frequency’ waves, but the coupling happens in the high-frequency, large wavenumber limit, and it occurs at phase matching conditions for the pump, seed and plasma waves, such as
![]() $\unicode[STIX]{x1D714}_{pump}=\unicode[STIX]{x1D714}_{seed}+\unicode[STIX]{x1D714}_{plasma}$
. Using higher pump and seed frequencies could potentially allow observation/exploitation of this phenomenon even in systems with large skin depths.
$\unicode[STIX]{x1D714}_{pump}=\unicode[STIX]{x1D714}_{seed}+\unicode[STIX]{x1D714}_{plasma}$
. Using higher pump and seed frequencies could potentially allow observation/exploitation of this phenomenon even in systems with large skin depths.
Also related to the density threshold for collective effects is the question of to what degree quasi-neutrality is a necessary condition, either on smaller scales or in the plasma as a whole. Experimental investigations of low-density, magnetically confined plasmas in a continuum ranging from pure electron plasmas to quasi-neutral electron–ion plasmas found that fluctuations are very different for different degrees of non-neutrality (Sarasola & Pedersen Reference Sarasola and Pedersen2012). Given that predictions for the microstability of electron–positron plasmas are very different from those for electron–ion plasmas, however, it would not be surprising if the relative importance of quasi-neutrality is also different in these systems.
For pair plasmas, simulations predict similar behaviour in electron/positron clouds that are non-neutral with a ratio of
![]() $55\,\%/45\,\%$
to clouds that are quasi-neutral (Sarri et al.
Reference Sarri, Poder, Cole, Schumaker, Di Piazza, Reville, Dzelzainis, Doria, Gizzi and Grittani2015). Magnetization is also a factor; theoretical investigations of different degrees of neutrality in pair plasmas indicate that even a small fraction of positrons in an electron-rich plasma can cause substantial modification to the properties of waves near the electron cyclotron resonance (Melrose Reference Melrose1997). To summarize, the importance of quasi-neutrality might well be different for pair plasma than it is for electron–ion plasmas, as well as being different for magnetized plasmas than it is for non-magnetized plasmas.
$55\,\%/45\,\%$
to clouds that are quasi-neutral (Sarri et al.
Reference Sarri, Poder, Cole, Schumaker, Di Piazza, Reville, Dzelzainis, Doria, Gizzi and Grittani2015). Magnetization is also a factor; theoretical investigations of different degrees of neutrality in pair plasmas indicate that even a small fraction of positrons in an electron-rich plasma can cause substantial modification to the properties of waves near the electron cyclotron resonance (Melrose Reference Melrose1997). To summarize, the importance of quasi-neutrality might well be different for pair plasma than it is for electron–ion plasmas, as well as being different for magnetized plasmas than it is for non-magnetized plasmas.
7 Summary
Motivated by the observation that different approaches to electron/positron pair plasma creation may result in a system with linear dimensions smaller than the plasma skin depth or the Debye length (or both), we have reviewed the physics associated with these two parameters. The Debye length being larger than the system implies that quasi-neutrality cannot be assumed (at least, not for anything smaller than the system in its entirety) and that the system cannot generate electrostatic potentials that can compete with thermal effects. The skin depth being larger than the system implies that some of the wave physics that would otherwise be interesting/useful (e.g. for reflectometry) are not accessible, and that any wave that fits in the system involves faster time scales than that involved in Debye shielding.
Neither multiple skin depths nor multiple Debye lengths, however, is strictly necessary for the observation of collective phenomena, as evidenced for example by experiments involving two-stream instabilities. The transition from ‘single particle’ behaviour to ‘collective’ behaviour, like the transition from ‘non-neutral’ to ‘quasi-neutral’ plasma, is far from being fully understood. What these transitions look like – whether they are gradual or sharp with respect to different parameters, to what extent different plasma parameters are more or less influential and so on – is a compelling topic of ongoing research.
Acknowledgements
The authors acknowledge valuable discussions with H. Saitoh and U. Hergenhahn. E.V.S. acknowledges funding from the Helmholtz Association.