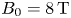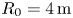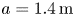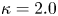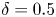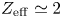1. Introduction
Fusion energy has the potential to provide nearly limitless greenhouse gas (GHG) emission-free energy without operational limitations arising from the time of day, ambient weather conditions or geographical location. As such, it could serve as an excellent partner for other zero-emission energy sources such as solar, wind and hydroelectric power, by reducing the amount of excess capacity, long-term grid-scale storage and demand curtailment required to ensure continuously available electricity, without the waste storage and licensing issues associated with fission energy. Thus, this partnership could deliver sustainable GHG-free energy at a lower cost and greater grid resiliency than a power grid which utilizes only variable energy sources (Clack et al. Reference Clack, Qvist, Apt, Bazilian, Brandt, Caldeira, Davis, Diakov, Handschy and Hines2017; Sepulveda et al. Reference Sepulveda, Jenkins, de Sisternes and Lester2018; Tynan & Abdulla Reference Tynan and Abdulla2020; Handley, Slesinski & Hsu Reference Handley, Slesinski and Hsu2021). However, fusion must be able to provide timely and economically attractive solutions if it is to play a meaningful role in decarbonization of the global energy system by mid-century, or contribute to near-term energy security and independence. Through recent strategic planning activities (APS-DPP Community Planning Process 2020; FESAC 2020) and National Academies of Science Engineering and Medicine (NASEM) studies (NASEM 2019, 2021), the US fusion community has embraced this challenge, stating in the opening of the 2021 ‘Powering the Future: Fusion & Plasmas’ report (FESAC 2020) that ‘Now is the time to move aggressively toward the deployment of fusion energy’. A common theme of these reports and studies is for the US fusion energy program to support the development, construction and operation of a fusion pilot plant on an aggressive time scale in partnership with private industry. As an example of these aggressive timeframes, the 2021 ‘Bringing Fusion to the U.S. Grid’ NASEM report's first recommendation is to ‘$\ldots$![]() produce net electricity in a fusion pilot plant in the United States in the 2035-2040 timeframe’, which is the same timeframe as when the long-awaited ITER experiment plans to begin deuterium-tritium operation (Bigot Reference Bigot2019).
produce net electricity in a fusion pilot plant in the United States in the 2035-2040 timeframe’, which is the same timeframe as when the long-awaited ITER experiment plans to begin deuterium-tritium operation (Bigot Reference Bigot2019).
While there are many possible definitions of the exact mission and requirements for a fusion pilot plant (FPP), the combination of advances in enabling technologies (Maingi et al. Reference Maingi, Lumsdaine, Allain, Chacon, Gourlay, Greenfield, Hughes, Humphreys, Izzo and McLean2019) such as high temperature superconductors and a rapidly changing energy marketplace has reinvigorated interest in the development of compact high-field FPP concepts, particularly tokamaks (which is the sole configuration considered in this paper). The 2019 NASEM report (NASEM 2019) defines a compact FPP as a ‘$\ldots$![]() pilot plant producing power similar to that expected in ITER but in a device much smaller in size and cost and employing design improvements that would allow net electricity production.’ Ideally, these compact approaches can integrate more easily into rapidly evolving energy grids, providing up to several hundreds of megawatts (MW) of baseload electric power from a facility with significantly reduced capital cost relative to larger fusion power plants (Najmabadi et al. Reference Najmabadi, Abdou, Bromberg, Brown, Chan, Chu, Dahlgren, El-Guebaly, Heitzenroeder and Henderson2006; Wan et al. Reference Wan, Ding, Qian, Li, Xiao and Xu2014; Kessel et al. Reference Kessel, Tillack, Najmabadi, Poli, Ghantous, Gorelenkov, Wang, Navaei, Toudeshki and Koehly2015; Kang et al. Reference Kang, Park, Jung, Kim, Wang, Lee, Na, Im, Na and Hwang2017; Tobita et al. Reference Tobita, Hiwatari, Sakamoto, Someya, Asakura, Utoh, Miyoshi, Tokunaga, Homma and Kakudate2019; Federici et al. Reference Federici, Holden, Baylard and Beaumont2021) targeting half a gigawatt or more electric power. However, the compact high-field path entails resolving physics and engineering issues such as large stresses on magnet coils and enormous edge exhaust fluxes which are even more daunting than what is faced in large lower-field concepts. Moreover, the solutions to these issues must be compatible with sustained high core plasma confinement and performance levels to produce sufficient amounts of fusion power from a relatively small volume. Even more stringent requirements on core performance and stability are required if truly steady-state non-inductive operation is required. To date, no device or concept has experimentally demonstrated the integration of a suitable edge heat exhaust mitigation strategy with sufficient sustained core confinement and stability at fusion-relevant parameters. It is therefore essential to resolve this integrated tokamak exhaust and performance (ITEP) gap (FESAC 2020) as soon as possible to assess the practical viability of compact high-field tokamaks as an FPP concept.
pilot plant producing power similar to that expected in ITER but in a device much smaller in size and cost and employing design improvements that would allow net electricity production.’ Ideally, these compact approaches can integrate more easily into rapidly evolving energy grids, providing up to several hundreds of megawatts (MW) of baseload electric power from a facility with significantly reduced capital cost relative to larger fusion power plants (Najmabadi et al. Reference Najmabadi, Abdou, Bromberg, Brown, Chan, Chu, Dahlgren, El-Guebaly, Heitzenroeder and Henderson2006; Wan et al. Reference Wan, Ding, Qian, Li, Xiao and Xu2014; Kessel et al. Reference Kessel, Tillack, Najmabadi, Poli, Ghantous, Gorelenkov, Wang, Navaei, Toudeshki and Koehly2015; Kang et al. Reference Kang, Park, Jung, Kim, Wang, Lee, Na, Im, Na and Hwang2017; Tobita et al. Reference Tobita, Hiwatari, Sakamoto, Someya, Asakura, Utoh, Miyoshi, Tokunaga, Homma and Kakudate2019; Federici et al. Reference Federici, Holden, Baylard and Beaumont2021) targeting half a gigawatt or more electric power. However, the compact high-field path entails resolving physics and engineering issues such as large stresses on magnet coils and enormous edge exhaust fluxes which are even more daunting than what is faced in large lower-field concepts. Moreover, the solutions to these issues must be compatible with sustained high core plasma confinement and performance levels to produce sufficient amounts of fusion power from a relatively small volume. Even more stringent requirements on core performance and stability are required if truly steady-state non-inductive operation is required. To date, no device or concept has experimentally demonstrated the integration of a suitable edge heat exhaust mitigation strategy with sufficient sustained core confinement and stability at fusion-relevant parameters. It is therefore essential to resolve this integrated tokamak exhaust and performance (ITEP) gap (FESAC 2020) as soon as possible to assess the practical viability of compact high-field tokamaks as an FPP concept.
One of the primary challenges for resolving the ITEP gap is in defining how big the gap is, given the wide range of potential FPP configurations and operating scenarios. For instance, it is vital to understand what mix of transport mechanisms will dominate in compact high-field tokamak FPPs, and whether they differ from current day experiments or what is expected in larger lower-field devices. Both core and edge transport must be well characterized to accurately predict and efficiently optimize reactor designs which can meet both the performance and exhaust requirements within engineering and economic constraints. It is also important to assess how accurate we believe current predictive models are when extrapolating to the compact high field FPP scenario parameters. Estimates of various FPP parameters and metrics (such as fusion energy gain, wall neutron loading or divertor heat flux width) can be made using combinations of systems codes (Dragojlovic et al. Reference Dragojlovic, Rene Raffray, Najmabadi, Kessel, Waganer, El-Guebaly and Bromberg2010; Stambaugh et al. Reference Stambaugh, Chan, Garofalo, Sawan, Humphreys, Lao, Leuer, Petrie, Prater and Snyder2011; Kessel et al. Reference Kessel, Tillack, Najmabadi, Poli, Ghantous, Gorelenkov, Wang, Navaei, Toudeshki and Koehly2015; Kovari et al. Reference Kovari, Fox, Harrington, Kembleton, Knight, Lux and Morris2016; Menard et al. Reference Menard, Brown, El-Guebaly, Boyer, Canik, Colling, Raman, Wang, Zhai and Buxton2016; Coleman & McIntosh Reference Coleman and McIntosh2019; Morris et al. Reference Morris, Coleman, Kahn, Muldrew, Pearce, Short, Cook, Desai, Humphrey and Kovari2021) and scaling laws for properties like global energy confinement (ITER Physics Expert Group on Confinement et al. 1999; Petty Reference Petty2008) or proximity to the Greenwald density limit (Greenwald Reference Greenwald2002). However, many (if not all) of these scaling laws are empirically derived from collections of limited experimental data, and their extrapolation to future burning plasmas with significantly different parameters, actuators and operating scenarios is inherently fraught with large uncertainty. Moreover, in some studies, parameters such as $H_{98(y,2)}$![]() (the ratio of the global energy confinement time to the value predicted by the $\tau _{98(y,2)}$
(the ratio of the global energy confinement time to the value predicted by the $\tau _{98(y,2)}$![]() scaling law ITER Physics Expert Group on Confinement et al. 1999) are effectively treated as free parameters to be varied or optimized upon, without specifying if or how these variations could be done in a manner consistent with the constraints placed on available actuators and engineering tolerances in the rest of the study. In fact, work by Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) has demonstrated that plasmas with the same size, confinement factor, density peaking and other typically used metrics can exhibit significantly different amounts of fusion gain. Given that the level of confinement achieved is typically one of the most impactful parameters on overall reactor cost (Wade & Leuer Reference Wade and Leuer2020), more sophisticated modelling is clearly needed to scope out potential FPP facilities and scenarios at a higher degree of fidelity and detail for the rapid development and deployment of fusion energy to be successful. While there are many aspects to resolving the ITEP challenge, one component that is relatively tractable to study with existing higher-fidelity modelling capabilities is examining what level of sustained performance can be achieved in a compact reactor using only the external actuators and edge exhaust solutions likely to be available in such a facility.
scaling law ITER Physics Expert Group on Confinement et al. 1999) are effectively treated as free parameters to be varied or optimized upon, without specifying if or how these variations could be done in a manner consistent with the constraints placed on available actuators and engineering tolerances in the rest of the study. In fact, work by Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) has demonstrated that plasmas with the same size, confinement factor, density peaking and other typically used metrics can exhibit significantly different amounts of fusion gain. Given that the level of confinement achieved is typically one of the most impactful parameters on overall reactor cost (Wade & Leuer Reference Wade and Leuer2020), more sophisticated modelling is clearly needed to scope out potential FPP facilities and scenarios at a higher degree of fidelity and detail for the rapid development and deployment of fusion energy to be successful. While there are many aspects to resolving the ITEP challenge, one component that is relatively tractable to study with existing higher-fidelity modelling capabilities is examining what level of sustained performance can be achieved in a compact reactor using only the external actuators and edge exhaust solutions likely to be available in such a facility.
Towards this end, we present in this paper the results of an integrated core plasma modelling (Poli Reference Poli2018) study undertaken with these issues in mind. Two compact high-field tokamak plasma core transport scenarios have been developed, corresponding to pulsed and fully steady-state operation. These predictions were made using the newly developed STEP integrated modelling capabilities (Meneghini et al. Reference Meneghini, Snoep, Lyons, McClenaghan, Imai, Grierson, Smith, Staebler, Snyder and Candy2020; Lyons et al. Reference Lyons, McClenaghan, Slendebroek, Meneghini, Neiser, Smith, Weisberg, Belli, Candy and Hanson2023) in the OMFIT workflow manager (Meneghini et al. Reference Meneghini, Smith, Lao, Izacard, Ren, Park, Candy, Wang, Luna and Izzo2015). In this study, we use the TGYRO transport solver (Candy et al. Reference Candy, Holland, Waltz, Fahey and Belli2009) to predict core density and temperature profiles, with NEO (Belli & Candy Reference Belli and Candy2008, Reference Belli and Candy2012) and TGLF (Staebler, Kinsey & Waltz Reference Staebler, Kinsey and Waltz2007; Staebler et al. Reference Staebler, Candy, Howard and Holland2016, Reference Staebler, Belli, Candy, Kinsey, Dudding and Patel2021) used to predict neoclassical and turbulent transport, respectively, and EPED (Snyder et al. Reference Snyder, Groebner, Leonard, Osborne and Wilson2009, Reference Snyder, Groebner, Hughes, Osborne, Beurskens, Leonard, Wilson and Xu2011) to provide pedestal boundary conditions. Our goal in developing these initial scenarios was to simply assemble self-consistent core plasma equilibria and transport solutions, using high fidelity but still practical predictive modelling capabilities. We refer to the scenarios as ‘use cases’ in this paper because we intend for them to provide the nominal parameters and starting points for more detailed core transport studies in the future, such as verification and benchmarking of different quasilinear and nonlinear turbulent transport models in a manner similar to how the CYCLONE base case parameters (Dimits et al. Reference Dimits, Bateman, Beer, Cohen, Dorland, Hammett, Kim, Kinsey, Kotschenreuther and Kritz2000) have been used. Therefore, we have not undertaken any sort of detailed optimization of the scenarios with regards to parameters such as aspect ratio, plasma current $I_p$![]() or recirculating power fraction. Instead, we use a combination of parameters and high-level assumptions consistent with previous compact tokamak modelling studies (Sorbom et al. Reference Sorbom, Ball, Palmer, Mangiarotti, Sierchio, Bonoli, Kasten, Sutherland, Barnard and Haakonsen2015; Menard et al. Reference Menard, Brown, El-Guebaly, Boyer, Canik, Colling, Raman, Wang, Zhai and Buxton2016; Buttery et al. Reference Buttery, Park, McClenaghan, Weisberg, Canik, Ferron, Garofalo, Holcomb, Leuer and Snyder2021) to constrain the conditions considered and performance required. Keeping with the well-established conventions of the fusion field, which require the regular creation of new acronyms for new scenarios and facilities, we christen the pulsed and steady-state use cases presented here UCR-P (use case reactor – pulsed) and UCR-SS (use case reactor – steady state). Alternatively, or additionally, the UC in these acronyms could be taken to represent (U)noptimized (C)ompact.
or recirculating power fraction. Instead, we use a combination of parameters and high-level assumptions consistent with previous compact tokamak modelling studies (Sorbom et al. Reference Sorbom, Ball, Palmer, Mangiarotti, Sierchio, Bonoli, Kasten, Sutherland, Barnard and Haakonsen2015; Menard et al. Reference Menard, Brown, El-Guebaly, Boyer, Canik, Colling, Raman, Wang, Zhai and Buxton2016; Buttery et al. Reference Buttery, Park, McClenaghan, Weisberg, Canik, Ferron, Garofalo, Holcomb, Leuer and Snyder2021) to constrain the conditions considered and performance required. Keeping with the well-established conventions of the fusion field, which require the regular creation of new acronyms for new scenarios and facilities, we christen the pulsed and steady-state use cases presented here UCR-P (use case reactor – pulsed) and UCR-SS (use case reactor – steady state). Alternatively, or additionally, the UC in these acronyms could be taken to represent (U)noptimized (C)ompact.
The remainder of the paper is structured as follows. In § 2, the methodology and workflow used to create use cases are detailed. The key finding is that both the UCR-P and UCR-SS use cases can meet the goal of producing 200 MW or more net electric power while maintaining margin against disruption risk via edge safety factor $q_{95} \ge 5$![]() and pedestal density equal to ${\sim }80\,\%$
and pedestal density equal to ${\sim }80\,\%$![]() of the Greenwald density in a $B_0 = 8 \,\mathrm {T}$
of the Greenwald density in a $B_0 = 8 \,\mathrm {T}$![]() , $R_0 = 4 \,\mathrm {m}$
, $R_0 = 4 \,\mathrm {m}$![]() , $Z_{{\rm eff}} \sim 2$
, $Z_{{\rm eff}} \sim 2$![]() tokamak, depending upon the specific transport model used and assumptions made. Here, $q_{95}$
tokamak, depending upon the specific transport model used and assumptions made. Here, $q_{95}$![]() is the average safety factor evaluated on the flux surface enclosing 95 % of the poloidal magnetic flux. In particular, the original TGLF SAT0 saturation rule yields the most optimistic predictions for the default assumptions made, with the more recent SAT1 and SAT2 rules yielding increasingly pessimistic predictions at fixed input parameters such as field, current and impurity ion concentrations. The core transport of these plasmas is documented in § 3, with key similarities and differences between the use cases highlighted. We demonstrate that the sensitivity of the predicted performance to transport model choice arises from different levels of transport stiffness each model exhibits, combined with the fact that these scenarios have gyroBohm-normalized fluxes an order of magnitude larger than other high confinement (H-mode) burning and non-burning plasmas. In § 4, some broader implications for transport in a tokamak power plant are discussed, including a general picture of transport in reactor scenarios which can be used to characterize current and future plasmas, as well as guide future studies. Conclusions and next steps for future research are presented in § 5.
is the average safety factor evaluated on the flux surface enclosing 95 % of the poloidal magnetic flux. In particular, the original TGLF SAT0 saturation rule yields the most optimistic predictions for the default assumptions made, with the more recent SAT1 and SAT2 rules yielding increasingly pessimistic predictions at fixed input parameters such as field, current and impurity ion concentrations. The core transport of these plasmas is documented in § 3, with key similarities and differences between the use cases highlighted. We demonstrate that the sensitivity of the predicted performance to transport model choice arises from different levels of transport stiffness each model exhibits, combined with the fact that these scenarios have gyroBohm-normalized fluxes an order of magnitude larger than other high confinement (H-mode) burning and non-burning plasmas. In § 4, some broader implications for transport in a tokamak power plant are discussed, including a general picture of transport in reactor scenarios which can be used to characterize current and future plasmas, as well as guide future studies. Conclusions and next steps for future research are presented in § 5.
2. Methods
In this section, we detail the methodology used to develop the UCR-P and UCR-SS use cases, as well as the resulting equilibria and transport solutions. As alluded to in § 1, there is a wide range of possible mission scopes for an FPP and in what characteristics a commercial fusion power plant might have. Likewise, identifying the conditions needed to close the ITEP gap requires more quantitatively defining what level of plasma confinement is needed to meet the ‘sufficient sustained core confinement and stability at fusion-relevant parameters’ requirement. In this study, we choose to target compact high-field D-T plasma tokamak scenarios which would enable production of 200 MW or more net electric power as the practical measure of needed confinement and performance, in line with other recent compact tokamak studies. As the goal of this study is to investigate plasma physics rather than engineering or economical optimizations, a more physics-centred target such as production of 1 GW or more fusion power would be an equally valid and simpler choice. However, we choose the net electric power target to better incorporate the impact of auxiliary power needs and recirculating power fraction in guiding the design point. Regardless of the specific target chosen, the sheer range of possible choices regarding characteristics such as plasma shape, size, magnetic field, current, density and external actuator details makes the design (much less optimization) of a tokamak reactor quite daunting at first glance. However, there are also a wide range of engineering and plasma constraints which provide quite stringent limits on these choices, as described in e.g. the excellent review paper by Freidberg, Mangiarotti & Minervini (Reference Freidberg, Mangiarotti and Minervini2015). By combining these constraints with several additional assumptions detailed below, a straightforward path for determining many of the global scenario parameters emerges, which is laid out in § 2.1.
For these use cases to provide meaningful representations of a reactor plasma, production of significant fusion power is a necessary, but not sufficient, requirement. As identified by the ITEP gap, this production must also be sustained (i.e. the plasma must be stable on reactor operation time scales) and compatible with exhaust power handling. Moreover, engineering and recirculating power constraints limit what external plasma actuators are likely to be available in an economically attractive commercial reactor. We therefore identify three corresponding high-level constraints for the use case development choices.
(i) Stability. Beyond considering global limits of normalized plasma pressure $\beta _N = \beta /(I_p/aB)$
 , where $\beta = 2\mu _0nT/B^2$
, where $\beta = 2\mu _0nT/B^2$ , we will target plasmas with large edge safety factor and edge densities at least 20 % lower than the Greenwald density to reduce the likelihood of disruptions.
, we will target plasmas with large edge safety factor and edge densities at least 20 % lower than the Greenwald density to reduce the likelihood of disruptions.(ii) Exhaust power handling. The plasma is assumed to have a nearly constant $Z_{{\rm eff}} \sim 2$
 , and consists primarily of 85 % deuterium and tritium, 5 % thermal $\mathrm {He}^4$
, and consists primarily of 85 % deuterium and tritium, 5 % thermal $\mathrm {He}^4$ ash, and trace levels of argon and tungsten. Argon is assumed to be injected into the plasma edge to help provide a radiative mantle and reduce the divertor heat flux, while the tungsten arises from the inevitable plasma-wall interactions. Although modelling these edge physics and material interactions is well beyond the scope of this work, it is important to include their impacts (through dilution and radiation) on core plasma performance. The only deviation from constant $Z_{{\rm eff}}$
ash, and trace levels of argon and tungsten. Argon is assumed to be injected into the plasma edge to help provide a radiative mantle and reduce the divertor heat flux, while the tungsten arises from the inevitable plasma-wall interactions. Although modelling these edge physics and material interactions is well beyond the scope of this work, it is important to include their impacts (through dilution and radiation) on core plasma performance. The only deviation from constant $Z_{{\rm eff}}$ comes from inclusion of the energetic alpha particles (using a classical slowing down distribution), and corresponding reduction of the deuterium and tritium to maintain quasi-neutrality. All other impurities are assumed to have the same profile shape as the electron density.
comes from inclusion of the energetic alpha particles (using a classical slowing down distribution), and corresponding reduction of the deuterium and tritium to maintain quasi-neutrality. All other impurities are assumed to have the same profile shape as the electron density.(iii) External actuators. An extremely simplified model for specifying the auxiliary sources is used, which is intended to represent radiofrequency (RF) wave injection that provides only electron heating and current drive. Ion cyclotron radio frequency (ICRF) heating is not considered to simplify the modelling (i.e. no need for minority ion species or calculations of ion versus electron heating fractions). Neutral beam injection (NBI)-like sources that would also provide core particle fuelling, torque injection and direct ion heating are excluded, as well as any attempt to model core density fuelling via pellet injection.
We recognize that for each of these constraints, equally valid qualitatively and/or quantitatively different choices could be made, and emphasize that these choices are by no means the only possible selections. However, we believe they are representative of what previous studies have identified as acceptable given the many overlapping physics, engineering and economic constraints that must be accounted for, and so provide a suitable basis for guiding development of these use cases. Assessing how changes to these assumptions impact the predicted scenario parameters may be pursued in future studies. In particular, there is likely high potential for improved performance if sustained non-negligible rotation and/or core density peaking via NBI heating, pellet fuelling, externally driven resonant magnetic perturbations or other actuators can be obtained without unacceptable impacts to tritium breeding ratio, recirculating power and facility reliability. Thus, one may view the choice of only RF-like heating and current drive actuators as a simple but conservative one.
2.1. Determining the plasma shape, size, field and current
Building upon the constraints identified above, we now detail the sequence of considerations and choices made to more quantitatively define the global properties of the use cases. The approach here generally follows the logic and considerations described by Freidberg et al. (Reference Freidberg, Mangiarotti and Minervini2015) and Segal, Cerfon & Freidberg (Reference Segal, Cerfon and Freidberg2021), and we encourage the reader to examine those papers for additional details on how these various constraints and decisions interact. As above, the emphasis here was on selecting typical representative ‘round number’ values for various parameters, rather than any kind of careful optimization of the selections.
(i) Plasma size. We start by considering plasmas with major radius $R_0 = 4\,\mathrm {m}$
 and minor radius $a = 1.4\,\mathrm {m}$
and minor radius $a = 1.4\,\mathrm {m}$ , corresponding to an inverse aspect ratio $\epsilon = a/R_0 = 0.35$
, corresponding to an inverse aspect ratio $\epsilon = a/R_0 = 0.35$ . These values were chosen by seeking a reasonable trade-off between compactness (as defined in § 1) and the need for sufficient plasma volume to produce significant fusion power without exceeding wall neutron flux $\varGamma _{{\rm wall}}$
. These values were chosen by seeking a reasonable trade-off between compactness (as defined in § 1) and the need for sufficient plasma volume to produce significant fusion power without exceeding wall neutron flux $\varGamma _{{\rm wall}}$ limits, as well as providing enough inboard build space for a breeding blanket, shielding, toroidal field coils and solenoid.
limits, as well as providing enough inboard build space for a breeding blanket, shielding, toroidal field coils and solenoid.(ii) Plasma scenario and shape. We choose to focus on conventional H-mode operation for these use cases, as this is the operational scenario which has demonstrated the best sustained confinement to date, and for which the most complete modelling capabilities exist. Strongly shaped plasmas with large elongation and triangularity enable maximizing both the plasma volume and pedestal pressure at fixed radius and aspect ratio. However, engineering constraints on feedback coils (to maintain vertical stability) and shaping coils (to create the plasma triangularity and divertor field structure) limit their maximum values. Here, we choose to consider up-down symmetric plasmas with separatrix elongation $\kappa = 2$
 and triangularity $\delta = 0.5$
and triangularity $\delta = 0.5$ as reasonable ‘round number’ values representative of what was identified in the more careful and detailed previous system and design studies.
as reasonable ‘round number’ values representative of what was identified in the more careful and detailed previous system and design studies.(iii) Plasma field. Having determined the plasma size and shape, we choose an on-axis vacuum toroidal field $B_0 = 8\,\mathrm {T}$
 , which corresponds to a peak inboard on-coil field of $22\unicode{x2013}25\,\mathrm {T}$
, which corresponds to a peak inboard on-coil field of $22\unicode{x2013}25\,\mathrm {T}$ , depending on the specific inboard build choices. This on-coil field is quite large but consistent with recent assumptions on maximum acceptable structural forces on HTS coils (Sorbom et al. Reference Sorbom, Ball, Palmer, Mangiarotti, Sierchio, Bonoli, Kasten, Sutherland, Barnard and Haakonsen2015).
, depending on the specific inboard build choices. This on-coil field is quite large but consistent with recent assumptions on maximum acceptable structural forces on HTS coils (Sorbom et al. Reference Sorbom, Ball, Palmer, Mangiarotti, Sierchio, Bonoli, Kasten, Sutherland, Barnard and Haakonsen2015).(iv) Plasma current. Ensuring global stability next leads to constraints on plasma current and density. First, it is well known that the plasma must maintain a sufficiently large edge safety factor $q = r B_{\phi }/R B_{\theta }$
 to remain stable against external kink instabilities. While the exact value depends on the details of the plasma shape and internal current and pressure profiles, a practical rule is to target a value of $q_{95} > 3$
to remain stable against external kink instabilities. While the exact value depends on the details of the plasma shape and internal current and pressure profiles, a practical rule is to target a value of $q_{95} > 3$ , to be well above the hard limit of $q_{{\rm edge}} = 2$
, to be well above the hard limit of $q_{{\rm edge}} = 2$ . However, even above this limit, plasmas can disrupt, and evidence suggests that disruptivity decreases with larger edge safety factor at all values of normalized plasma pressure $\beta _N$
. However, even above this limit, plasmas can disrupt, and evidence suggests that disruptivity decreases with larger edge safety factor at all values of normalized plasma pressure $\beta _N$ (Gerhardt et al. Reference Gerhardt, Bell, Diallo, Gates, LeBlanc, Menard, Mueller, Sabbagh, Soukhanovskii and Tritz2013; Garofalo et al. Reference Garofalo, Abdou, Canik, Chan, Hyatt, Hill, Morley, Navratil, Sawan and Taylor2014). Given the potential for significant damage a disruption could inflict on the reactor vessel, we will target plasmas with $q_{95} \ge 5$
(Gerhardt et al. Reference Gerhardt, Bell, Diallo, Gates, LeBlanc, Menard, Mueller, Sabbagh, Soukhanovskii and Tritz2013; Garofalo et al. Reference Garofalo, Abdou, Canik, Chan, Hyatt, Hill, Morley, Navratil, Sawan and Taylor2014). Given the potential for significant damage a disruption could inflict on the reactor vessel, we will target plasmas with $q_{95} \ge 5$ to reduce the frequency and severity of potential current-driven disruptions and other global instabilities. Furthermore, as the divertor heat flux is expected to scale as $1/B_{\theta }$
to reduce the frequency and severity of potential current-driven disruptions and other global instabilities. Furthermore, as the divertor heat flux is expected to scale as $1/B_{\theta }$ (Eich et al. Reference Eich, Leonard, Pitts, Fundamenski, Goldston, Gray, Herrmann, Kirk, Kallenbach and Kardaun2013), targeting high edge safety factors corresponds to increased heat flux widths for fixed field and size, as well as possibly reduced edge localized mode (ELM) energy fractions due to the observed inverse collisionality dependence $\Delta W_{{\rm ELM}}/W_{{\rm ped}} \propto 1/\nu _e^*$
(Eich et al. Reference Eich, Leonard, Pitts, Fundamenski, Goldston, Gray, Herrmann, Kirk, Kallenbach and Kardaun2013), targeting high edge safety factors corresponds to increased heat flux widths for fixed field and size, as well as possibly reduced edge localized mode (ELM) energy fractions due to the observed inverse collisionality dependence $\Delta W_{{\rm ELM}}/W_{{\rm ped}} \propto 1/\nu _e^*$ (where $\nu _e^* =(R/r)^{3/2}qR\nu _e /v_{{\rm th},e}$
(where $\nu _e^* =(R/r)^{3/2}qR\nu _e /v_{{\rm th},e}$ ) (Loarte et al. Reference Loarte, Lipschultz, Kukushkin, Matthews, Stangeby, Asakura, Counsell, Federici, Kallenbach and Krieger2007). For the size, shape and magnetic field values determined above, this requirement translates to a plasma current $I_p$
) (Loarte et al. Reference Loarte, Lipschultz, Kukushkin, Matthews, Stangeby, Asakura, Counsell, Federici, Kallenbach and Krieger2007). For the size, shape and magnetic field values determined above, this requirement translates to a plasma current $I_p$ of 16 MA or lower. In this work, we therefore examine an inductive 16 MA use case (UCR-P), as well as a 12 MA steady-state use case (UCR-SS). The lower $I_p$
of 16 MA or lower. In this work, we therefore examine an inductive 16 MA use case (UCR-P), as well as a 12 MA steady-state use case (UCR-SS). The lower $I_p$ value is chosen for UCR-SS based on the need to minimize the expensive external current drive needed and maximize the bootstrap current fraction, as both favour lower current operation. These goals are balanced against the need for sufficient operating density (as described by the next constraint) and energy confinement time (which generally increases with current).
value is chosen for UCR-SS based on the need to minimize the expensive external current drive needed and maximize the bootstrap current fraction, as both favour lower current operation. These goals are balanced against the need for sufficient operating density (as described by the next constraint) and energy confinement time (which generally increases with current).(v) Plasma density. A second stability-driven constraint comes in the form of the Greenwald density $n_G = I_p/{\rm \pi} a^2$
 (Greenwald Reference Greenwald2002). Empirically, when the line-averaged density of plasmas approaches or exceeds this value, the plasma often suffers degraded confinement and/or disrupts. However, it is known that H-mode plasmas with peaked density profiles can significantly exceed this value (Maingi & Mahdavi Reference Maingi and Mahdavi2005), and recent experimental and theoretical studies suggest that the H-mode density limit may be more appropriately correlated with edge conditions such as collisionality or proximity to ideal stability bounds than the overall line-averaged density (Huber et al. Reference Huber, Bernert, Brezinsek, Chankin, Sergienko, Huber, Wiesen, Abreu, Beurskens and Boboc2017; Eich et al. Reference Eich, Goldston, Kallenbach, Sieglin and Sun2018; Singh & Diamond Reference Singh and Diamond2021; Sun et al. Reference Sun, Goldston, Huber, Xu, Flanagan, McDonald, de la Luna, Maslov, Harrison and Militello2021; Giacomin et al. Reference Giacomin, Pau, Ricci, Sauter and Eich2022). Based on these results, and consistent with some other recent compact reactor studies, we impose a constraint of pedestal density $n_{{\rm ped}} = 0.8 n_G$
(Greenwald Reference Greenwald2002). Empirically, when the line-averaged density of plasmas approaches or exceeds this value, the plasma often suffers degraded confinement and/or disrupts. However, it is known that H-mode plasmas with peaked density profiles can significantly exceed this value (Maingi & Mahdavi Reference Maingi and Mahdavi2005), and recent experimental and theoretical studies suggest that the H-mode density limit may be more appropriately correlated with edge conditions such as collisionality or proximity to ideal stability bounds than the overall line-averaged density (Huber et al. Reference Huber, Bernert, Brezinsek, Chankin, Sergienko, Huber, Wiesen, Abreu, Beurskens and Boboc2017; Eich et al. Reference Eich, Goldston, Kallenbach, Sieglin and Sun2018; Singh & Diamond Reference Singh and Diamond2021; Sun et al. Reference Sun, Goldston, Huber, Xu, Flanagan, McDonald, de la Luna, Maslov, Harrison and Militello2021; Giacomin et al. Reference Giacomin, Pau, Ricci, Sauter and Eich2022). Based on these results, and consistent with some other recent compact reactor studies, we impose a constraint of pedestal density $n_{{\rm ped}} = 0.8 n_G$ in our use cases, rather than on the overall line-average density.
in our use cases, rather than on the overall line-average density.(vi) Pedestal pressure. Finally, the choices above allow us to predict the pedestal pressure magnitude and structure via the EPED model, which has been extensively validated against current-day tokamaks. When combined with the imposed pedestal density constraint, this prediction of pedestal pressure is equivalent to a prediction of pedestal temperature (with the further assumption of equal ion and electron pedestal temperatures $T_{i,{\rm ped}} = T_{e,{\rm ped}}$
 ). However, it should also be emphasized that the extremely stiff core transport of burning plasmas (as will be demonstrated below) magnifies any uncertainties or errors in the assumed pedestal density and temperature levels. This sensitivity is particularly crucial, given that EPED predicts the maximum pedestal pressure for type-I ELMing discharges, based on a combination of peeling-ballooning (PBM) and kinetic ballooning mode stability (KBM) constraints. Unfortunately, if not mitigated, such ELMs would likely lead to unmanageable divertor heat fluxes in an actual reactor, raising the question as to how applicable the model is for this regime. It should be noted that EPED has demonstrated similar fidelity predicting pedestals of some ELM-free scenarios such as QH-mode as the type-I ELMing discharges (Snyder et al. Reference Snyder, Osborne, Burrell, Groebner, Leonard, Nazikian, Orlov, Schmitz, Wade and Wilson2012), suggesting that its use as a tool for investigating such scenarios is still a reasonable starting point. Additionally, at a practical level, the absence of equivalent predictive models for inherently ELM-free or mitigated ELM scenarios means that the MHD stability constraint approach is the only currently available validated means for predicting the relationship between global parameters such as shaping and field strength to the plasma in this region. Alternatively, the strong core transport stiffness means one can view the pedestal top temperatures used here as effective core boundary conditions as the minimal values that must be achieved by some manipulation of plasma shaping, edge fuelling or other actuators to produce the required fusion power and gain, independent of the near-edge or scrape-off layer plasma details. Clearly this assumption is a strong one, and developing capabilities to predict transport and near-edge profiles in ELM-free and/or ELM-mitigated regimes will be vital for identifying more robust reactor scenarios in the future that should be pursued urgently.
). However, it should also be emphasized that the extremely stiff core transport of burning plasmas (as will be demonstrated below) magnifies any uncertainties or errors in the assumed pedestal density and temperature levels. This sensitivity is particularly crucial, given that EPED predicts the maximum pedestal pressure for type-I ELMing discharges, based on a combination of peeling-ballooning (PBM) and kinetic ballooning mode stability (KBM) constraints. Unfortunately, if not mitigated, such ELMs would likely lead to unmanageable divertor heat fluxes in an actual reactor, raising the question as to how applicable the model is for this regime. It should be noted that EPED has demonstrated similar fidelity predicting pedestals of some ELM-free scenarios such as QH-mode as the type-I ELMing discharges (Snyder et al. Reference Snyder, Osborne, Burrell, Groebner, Leonard, Nazikian, Orlov, Schmitz, Wade and Wilson2012), suggesting that its use as a tool for investigating such scenarios is still a reasonable starting point. Additionally, at a practical level, the absence of equivalent predictive models for inherently ELM-free or mitigated ELM scenarios means that the MHD stability constraint approach is the only currently available validated means for predicting the relationship between global parameters such as shaping and field strength to the plasma in this region. Alternatively, the strong core transport stiffness means one can view the pedestal top temperatures used here as effective core boundary conditions as the minimal values that must be achieved by some manipulation of plasma shaping, edge fuelling or other actuators to produce the required fusion power and gain, independent of the near-edge or scrape-off layer plasma details. Clearly this assumption is a strong one, and developing capabilities to predict transport and near-edge profiles in ELM-free and/or ELM-mitigated regimes will be vital for identifying more robust reactor scenarios in the future that should be pursued urgently.
Given these choices, our task becomes identifying possible combinations of external actuators to generate plasmas with sufficient core confinement for the specified shape, field, total current and pedestal boundary conditions, while also being consistent with global pressure limits, the L–H power threshold, and considerations on actuator efficiency and recirculating power. Because this analysis does not include any detailed edge modelling or divertor design, we do not make any specific requirements on the divertor heat flux per se. However, it is briefly addressed further in § 3 in the discussion of L–H power thresholds and radiated power fractions. Finally, as above, we emphasize that these choices are by no means unique and almost certainly not ‘optimal’ with respect to any one criterion. Nonetheless, we believe they are likely representative of what considerations and trade-offs will be required for a compact reactor design that simultaneously respects physics, engineering and economic constraints.
2.2. STEP workflow
The integrated modelling workflow built in STEP illustrated in figure 1 is used to generate the use-case profiles and equilibria. Magnetohydrodynamic (MHD) stability of the use cases is assessed once a converged solution is obtained and is further discussed in § 2.3. The EPED pedestal pressure predictions generated at the end of the scenario constraint sequence in § 2.1 provide the initial conditions for these calculations. To predict the pedestal height and width, EPED must calculate the stability of various global magnetic equilibria constructed with model profiles, and these equilibria can also be used as starting conditions for integrated core transport modelling and stability analysis.

Figure 1. Schematic overview of STEP workflow used to generate the UCR-P and UCR-SS use cases.
The key features of the EPED predictions for both UCR-P and UCR-SS are shown in figure 2. For both use cases, EPED predicts total pedestal pressure to increase with pedestal density up to at least the Greenwald limit for each case (figure 2a), consistent with the pedestal in both cases being peeling rather than ballooning-limited (Snyder et al. Reference Snyder, Groebner, Leonard, Osborne and Wilson2009). However, the increase in pressure with density is weaker than linear, such that the predicted pedestal temperature decreases as the pedestal density increases (figure 2b). The strong sensitivity of pedestal temperature to changes in triangularity (at fixed density) is shown in figure 2(c), illustrating the motivation to use the strongest shaped plasma that engineering constraints can support. Finally, and perhaps most interestingly, the lack of predicted pedestal temperature to variations in $\beta _{N}$![]() for both cases (again at fixed pedestal density) is shown in figure 2(d). This result reflects the fact that while increasing normalized plasma pressure will increase the Shafranov shift and thereby help stabilize ballooning-limited pedestals, the current-gradient driven peeling modes are relatively insensitive to this physics (Snyder et al. Reference Snyder, Groebner, Hughes, Osborne, Beurskens, Leonard, Wilson and Xu2011). For this study, the more practical implication of this result is that the pedestal pressure can be kept as a fixed boundary condition during the core transport modelling (which will lead to changes in $\beta _{N}$
for both cases (again at fixed pedestal density) is shown in figure 2(d). This result reflects the fact that while increasing normalized plasma pressure will increase the Shafranov shift and thereby help stabilize ballooning-limited pedestals, the current-gradient driven peeling modes are relatively insensitive to this physics (Snyder et al. Reference Snyder, Groebner, Hughes, Osborne, Beurskens, Leonard, Wilson and Xu2011). For this study, the more practical implication of this result is that the pedestal pressure can be kept as a fixed boundary condition during the core transport modelling (which will lead to changes in $\beta _{N}$![]() as a self-consistent solution is found), rather than needing to continually update it self-consistently along with the core. Although this updating process is straightforward and has been used in previous studies (not all of which used OMFIT or STEP) (Meneghini et al. Reference Meneghini, Smith, Lao, Izacard, Ren, Park, Candy, Wang, Luna and Izzo2015, Reference Meneghini, Snoep, Lyons, McClenaghan, Imai, Grierson, Smith, Staebler, Snyder and Candy2020; Luda et al. Reference Luda, Angioni, Dunne, Fable, Kallenbach, Bonanomi, Schneider, Siccinio and Tardini2020), it does involve a non-trivial additional amount of computational time, which can significantly slow the overall workflow time to convergence. Therefore, unless otherwise noted, for the rest of this study, we take a fixed pedestal temperature $T_{i,{\rm ped}} = T_{e,{\rm ped}} = 3.5 \,\mathrm {keV}$
as a self-consistent solution is found), rather than needing to continually update it self-consistently along with the core. Although this updating process is straightforward and has been used in previous studies (not all of which used OMFIT or STEP) (Meneghini et al. Reference Meneghini, Smith, Lao, Izacard, Ren, Park, Candy, Wang, Luna and Izzo2015, Reference Meneghini, Snoep, Lyons, McClenaghan, Imai, Grierson, Smith, Staebler, Snyder and Candy2020; Luda et al. Reference Luda, Angioni, Dunne, Fable, Kallenbach, Bonanomi, Schneider, Siccinio and Tardini2020), it does involve a non-trivial additional amount of computational time, which can significantly slow the overall workflow time to convergence. Therefore, unless otherwise noted, for the rest of this study, we take a fixed pedestal temperature $T_{i,{\rm ped}} = T_{e,{\rm ped}} = 3.5 \,\mathrm {keV}$![]() for both cases, with corresponding fixed pedestal electron densities of $n_{e,{\rm ped}} = 1.5\times 10^{20} \,\mathrm {m}^{-3}$
for both cases, with corresponding fixed pedestal electron densities of $n_{e,{\rm ped}} = 1.5\times 10^{20} \,\mathrm {m}^{-3}$![]() (UCR-SS) or $2.0\times 10^{20} \,\mathrm {m}^{-3}$
(UCR-SS) or $2.0\times 10^{20} \,\mathrm {m}^{-3}$![]() (UCR-P), equivalent to $n_{e,{\rm ped}}/n_G \simeq 0.8$
(UCR-P), equivalent to $n_{e,{\rm ped}}/n_G \simeq 0.8$![]() . We note that these observations of pedestal dependence are also quite consistent with other burning plasmas predicted to have low collisionality pedestals and moderate shaping, including ITER (Snyder et al. Reference Snyder, Groebner, Hughes, Osborne, Beurskens, Leonard, Wilson and Xu2011) and SPARC (Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020, Reference Rodriguez-Fernandez, Creely, Greenwald, Brunner, Ballinger, Chrobak, Garnier, Granetz, Hartwig and Howard2022a).
. We note that these observations of pedestal dependence are also quite consistent with other burning plasmas predicted to have low collisionality pedestals and moderate shaping, including ITER (Snyder et al. Reference Snyder, Groebner, Hughes, Osborne, Beurskens, Leonard, Wilson and Xu2011) and SPARC (Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020, Reference Rodriguez-Fernandez, Creely, Greenwald, Brunner, Ballinger, Chrobak, Garnier, Granetz, Hartwig and Howard2022a).

Figure 2. EPED predictions of (a) pedestal pressure and (b–d) temperature as a function of (a,b) pedestal density, (c) triangularity $\delta$![]() and (d) normalized pressure $\beta _{N}$
and (d) normalized pressure $\beta _{N}$![]() in the $I_p = 16 \,\mathrm {MA}$
in the $I_p = 16 \,\mathrm {MA}$![]() inductive UCR-P use case ($\blacksquare$
inductive UCR-P use case ($\blacksquare$![]() , blue) and $I_p = 12 \,\mathrm {MA}$
, blue) and $I_p = 12 \,\mathrm {MA}$![]() steady-state UCR-SS scenario (
steady-state UCR-SS scenario (![]() , red).
, red).
Starting from the EPED calculations, the workflow then iterates between calculating a self-consistent Grad–Shafranov magnetic equilibrium solution for the specified fixed pressure and current profiles, and a transport solution that predicts plasma density and temperature profiles for a static magnetic equilibrium and external heating sources, as shown in figure 1. As such, it aims only to capture steady-state or time-averaged profiles, and does not attempt to examine dynamical time-dependent behaviour (including accessing the predicted states from initiation of the plasma discharge). The questions of plasma access and dynamic stability are highly challenging research topics in their own right and are beyond the scope of this study. Here, we only aim to identify potential targets for further study and refinement that might merit addressing of the dynamics in future work.
The determination of the magnetic equilibrium itself involves three steps, which are themselves consecutively iterated until a converged equilibrium is determined. The first step is to specify the external heating and current drive sources using the CHEF (current drive, heating and fuelling) OMFIT module. For this initial study, we specify Gaussian deposition profiles as a proxy of highly idealized RF heating sources, with an assumed current drive efficiency $\eta _{{\rm CD}} = n_{20} R I_{{\rm CD}}/P_{{\rm CD}} = 0.4$![]() , consistent with a number of previous studies (Freidberg et al. Reference Freidberg, Mangiarotti and Minervini2015; Sorbom et al. Reference Sorbom, Ball, Palmer, Mangiarotti, Sierchio, Bonoli, Kasten, Sutherland, Barnard and Haakonsen2015; Wade & Leuer Reference Wade and Leuer2020; Buttery et al. Reference Buttery, Park, McClenaghan, Weisberg, Canik, Ferron, Garofalo, Holcomb, Leuer and Snyder2021; Segal et al. Reference Segal, Cerfon and Freidberg2021) (with $n_{20}$
, consistent with a number of previous studies (Freidberg et al. Reference Freidberg, Mangiarotti and Minervini2015; Sorbom et al. Reference Sorbom, Ball, Palmer, Mangiarotti, Sierchio, Bonoli, Kasten, Sutherland, Barnard and Haakonsen2015; Wade & Leuer Reference Wade and Leuer2020; Buttery et al. Reference Buttery, Park, McClenaghan, Weisberg, Canik, Ferron, Garofalo, Holcomb, Leuer and Snyder2021; Segal et al. Reference Segal, Cerfon and Freidberg2021) (with $n_{20}$![]() the density in units of $10^{20} \,\mathrm {m}^{-3}$
the density in units of $10^{20} \,\mathrm {m}^{-3}$![]() ). While the UCR-P results are insensitive to the value chosen because no RF-driven current is assumed for that scenario (as it would be negligible relative to the Ohmic current), it should be noted that availability of some off-axis current drive capability in a UCR-P-like scenario is likely to be desirable for stabilization of tearing modes at the $q = 3/2$
). While the UCR-P results are insensitive to the value chosen because no RF-driven current is assumed for that scenario (as it would be negligible relative to the Ohmic current), it should be noted that availability of some off-axis current drive capability in a UCR-P-like scenario is likely to be desirable for stabilization of tearing modes at the $q = 3/2$![]() and $q = 2$
and $q = 2$![]() surfaces. The UCR-SS results are of course quite sensitive to the current drive modelling assumptions. In particular, obtaining the desired stable self-organized steady-state condition with a significant bootstrap fraction requires careful tailoring of the externally driven current profile and magnitude, which in turn impacts recirculating power and net electricity production. For the inductive scenarios, the ONETWO code (St John et al. Reference St John, Taylor, Lin-Liu and Turnbull1994) is then used to determine self-consistent Ohmic and bootstrap currents (using the Sauter model Sauter, Angioni & Lin-Liu Reference Sauter, Angioni and Lin-Liu1999, Reference Sauter, Angioni and Lin-Liu2002), as well as the classical fast alpha density profile. A similar procedure is used for the steady-state scenario, except that the drift-kinetic NEO code is used to calculate the bootstrap current instead of the ONETWO Sauter implementation, as the solution is highly dependent on the accuracy of this calculation. As will be shown below, for the scenario considered here, the two approaches give essentially equivalent predictions for the bootstrap current in the outer half of the plasma (including the pedestal), but NEO predicts a slightly lower bootstrap current at smaller radii. Finally, the CHEASE Grad–Shafranov solver (Lütjens, Bondeson & Sauter Reference Lütjens, Bondeson and Sauter1996) is run in a fixed-boundary mode to calculate an updated magnetic equilibrium given the updated pressure and current profiles generated by CHEF and ONETWO. This sequence is typically iterated 2–3 times until the resulting magnetic equilibrium is converged.
surfaces. The UCR-SS results are of course quite sensitive to the current drive modelling assumptions. In particular, obtaining the desired stable self-organized steady-state condition with a significant bootstrap fraction requires careful tailoring of the externally driven current profile and magnitude, which in turn impacts recirculating power and net electricity production. For the inductive scenarios, the ONETWO code (St John et al. Reference St John, Taylor, Lin-Liu and Turnbull1994) is then used to determine self-consistent Ohmic and bootstrap currents (using the Sauter model Sauter, Angioni & Lin-Liu Reference Sauter, Angioni and Lin-Liu1999, Reference Sauter, Angioni and Lin-Liu2002), as well as the classical fast alpha density profile. A similar procedure is used for the steady-state scenario, except that the drift-kinetic NEO code is used to calculate the bootstrap current instead of the ONETWO Sauter implementation, as the solution is highly dependent on the accuracy of this calculation. As will be shown below, for the scenario considered here, the two approaches give essentially equivalent predictions for the bootstrap current in the outer half of the plasma (including the pedestal), but NEO predicts a slightly lower bootstrap current at smaller radii. Finally, the CHEASE Grad–Shafranov solver (Lütjens, Bondeson & Sauter Reference Lütjens, Bondeson and Sauter1996) is run in a fixed-boundary mode to calculate an updated magnetic equilibrium given the updated pressure and current profiles generated by CHEF and ONETWO. This sequence is typically iterated 2–3 times until the resulting magnetic equilibrium is converged.
The new equilibrium, along with the kinetic profiles and auxiliary sources, is then used as an input to the TGYRO transport solver. Execution of TGYRO yields predictions of density and temperature profiles, assuming the magnetic equilibrium and external heating, fuelling and current drive sources are constant, by using the quasilinear TGLF model to predict turbulent fluxes and the NEO code to calculate neoclassical contributions. However, it will be shown in § 3 that neoclassical transport contributions are at best modest, and generally negligible, across the plasma core in both scenarios. Plasma rotation is assumed to be zero, consistent with no externally applied torque sources. As any plausible level of rotation in the plasma will almost certainly provide a net benefit through stabilization of turbulence and global instabilities, the neglect of possible ‘intrinsic’ rotation (Rice Reference Rice2016; Chrystal et al. Reference Chrystal, Grierson, Haskey, Sontag, Poli, Shafer and de Grassie2020) is a conservative assumption. TGYRO also self-consistently calculates internal heating sources such as fusion heating and radiative losses (cyclotron, bremsstrahlung and line radiation), as well as collisional energy exchange. Turbulent exchange processes (Manheimer, Ott & Tang Reference Manheimer, Ott and Tang1977; Hinton & Waltz Reference Hinton and Waltz2006; Zhao & Diamond Reference Zhao and Diamond2012; Candy Reference Candy2013) are predicted to be small by TGLF but are not included here as these predictions have not been well verified or validated. The TGYRO kinetic profile predictions can then be used to start another iteration of magnetic equilibrium refinement, and the process is continued until both equilibrium and profiles are converged. Achieving this convergence in the inductive UCR-P scenarios is relatively straightforward, as most of the current is Ohmically driven and not highly sensitive to small changes in kinetic profile values and gradients. However, in UCR-P, fully relaxed current profiles correspond to core safety factors well below unity. We therefore instead examine UCR-P solutions in which the core current density has been artificially diffused to obtain $q > 0.9$![]() everywhere (mimicking sawtooth relaxation), as well as ensuring only the bootstrap current contributes in the pedestal region. In contrast to UCR-P, achieving fully converged steady-state UCR-SS plasmas is significantly more challenging (both numerically and physics-wise), as there, the bootstrap current provides the majority of the total plasma current and is directly proportional to the local gradients. Moreover, the iterations and adjustments to the external current drive sources must continue until any Ohmic current has been eliminated in addition to fully converged profiles and equilibrium. In practice, given the discreteness of the TGYRO solver, stiffness of TGLF transport predictions and crudeness of the external current drive model used, the UCR-SS results were (somewhat arbitrarily) deemed sufficiently converged for their intended purpose when reasonably steady equilibria and profiles with less than 0.5 MA (out of 12 MA total) Ohmic current were obtained.
everywhere (mimicking sawtooth relaxation), as well as ensuring only the bootstrap current contributes in the pedestal region. In contrast to UCR-P, achieving fully converged steady-state UCR-SS plasmas is significantly more challenging (both numerically and physics-wise), as there, the bootstrap current provides the majority of the total plasma current and is directly proportional to the local gradients. Moreover, the iterations and adjustments to the external current drive sources must continue until any Ohmic current has been eliminated in addition to fully converged profiles and equilibrium. In practice, given the discreteness of the TGYRO solver, stiffness of TGLF transport predictions and crudeness of the external current drive model used, the UCR-SS results were (somewhat arbitrarily) deemed sufficiently converged for their intended purpose when reasonably steady equilibria and profiles with less than 0.5 MA (out of 12 MA total) Ohmic current were obtained.
Once a converged solution is obtained, the net electric power produced is determined using a workflow similar to what was used in previous reactor studies. Details of this calculation, including various assumed plant efficiencies, can be found in Appendix A. The key result of the analysis is that for the assumed efficiencies and power flow, the predicted net electric power production is calculated as
where $P_{{\rm aux}}$![]() is the amount of auxiliary heating power absorbed by the plasma and $Q_{{\rm fusion}} = P_{{\rm fusion}}/P_{{\rm aux}}$
is the amount of auxiliary heating power absorbed by the plasma and $Q_{{\rm fusion}} = P_{{\rm fusion}}/P_{{\rm aux}}$![]() the ratio of total fusion power produced to $P_{{\rm aux}}$
the ratio of total fusion power produced to $P_{{\rm aux}}$![]() . While not the focus of this paper, we emphasize that the two numerical coefficients of (2.1) are dominated by the assumed thermal efficiency of converting the thermal heat generated into electricity and the wall-plug efficiency of the auxiliary sources used, respectively. Although neither of these parameters is meaningfully dependent on plasma physics, even modest improvements to either can dramatically improve the overall economic attractiveness of a possible fusion power plant. It should also be noted that this calculation refers only to the power generated during the steady current flat-top phase of the UCR-P scenario, and does not take into account duty factor or pulse length impacts.
. While not the focus of this paper, we emphasize that the two numerical coefficients of (2.1) are dominated by the assumed thermal efficiency of converting the thermal heat generated into electricity and the wall-plug efficiency of the auxiliary sources used, respectively. Although neither of these parameters is meaningfully dependent on plasma physics, even modest improvements to either can dramatically improve the overall economic attractiveness of a possible fusion power plant. It should also be noted that this calculation refers only to the power generated during the steady current flat-top phase of the UCR-P scenario, and does not take into account duty factor or pulse length impacts.
2.3. Scenario results
For this analysis, the TGLF SAT1 saturation rule (Staebler et al. Reference Staebler, Candy, Howard and Holland2016) (with finite $\delta B_{\perp }$![]() fluctuations included) was used for predicting transport unless otherwise stated. The impact of different saturation rules and inclusion of magnetic fluctuations on the predicted transport is discussed further in §§ 3.2 and 3.3 below. Visualizations of the magnetic equilibria and pressure predicted by the process outlined above are shown in figure 3; note that the vessel first wall is included only for illustrative purposes and not used in any calculations. As might be expected, the steady-state scenario exhibits a significantly larger Shafranov shift of the magnetic axis and a corresponding elongation of the core magnetic surfaces relative to the inductive scenario.
fluctuations included) was used for predicting transport unless otherwise stated. The impact of different saturation rules and inclusion of magnetic fluctuations on the predicted transport is discussed further in §§ 3.2 and 3.3 below. Visualizations of the magnetic equilibria and pressure predicted by the process outlined above are shown in figure 3; note that the vessel first wall is included only for illustrative purposes and not used in any calculations. As might be expected, the steady-state scenario exhibits a significantly larger Shafranov shift of the magnetic axis and a corresponding elongation of the core magnetic surfaces relative to the inductive scenario.

Figure 3. (R,Z) pressure contours on closed magnetic surfaces in (a) UCR-P and (b) UCR-SS. The dashed lines indicated normalized poloidal flux contours of ${\psi _N = [0.2,0.4,0.6,0.8,0.95]}$![]() . The simplified vessel first wall is included only for illustrative purposes only and was not used in any calculations.
. The simplified vessel first wall is included only for illustrative purposes only and was not used in any calculations.
The corresponding density, temperature and safety factor profiles for both scenarios are shown in figure 4, and various associated parameters and metrics in table 1. The solid curves in figure 4 denote predictions with the density profile self-consistently evolved to predict zero net electron particle flux, while the dashed curves correspond to the results with peaked but fixed density profiles. The density profiles are prescribed to have a constant low but finite scale length in the central region of the plasma ($R/L_n \simeq 1$![]() ), chosen to give a level of peaking similar to the starting EPED model form predictions. These results are included to illustrate the sensitivity of the predictions to the choice of transport model physics, as recent studies by Howard et al. (Reference Howard, Rodriguez-Fernandez, Holland, Rice, Greenwald, Candy and Sciortino2021b) and Rodriguez-Fernandez, Howard & Candy (Reference Rodriguez-Fernandez, Howard and Candy2022b) have found that TGLF may underpredict density peaking relative to nonlinear gyrokinetic profile predictions made with CGYRO (Candy, Belli & Bravenec Reference Candy, Belli and Bravenec2016) in burning plasma conditions. In both use cases, the thermal impurity ions (He, Ar, W) are taken to have the same profile shape as the electron density, while the energetic alpha particles are assumed to have a fixed classical distribution calculated by ONETWO, and the thermal deuterium and tritium ions are required to be equal in magnitude with profiles determined via quasi-neutrality. The argon is assumed to be fully ionized, while the tungsten is treated as a single species with an effective charge $Z = 50$
), chosen to give a level of peaking similar to the starting EPED model form predictions. These results are included to illustrate the sensitivity of the predictions to the choice of transport model physics, as recent studies by Howard et al. (Reference Howard, Rodriguez-Fernandez, Holland, Rice, Greenwald, Candy and Sciortino2021b) and Rodriguez-Fernandez, Howard & Candy (Reference Rodriguez-Fernandez, Howard and Candy2022b) have found that TGLF may underpredict density peaking relative to nonlinear gyrokinetic profile predictions made with CGYRO (Candy, Belli & Bravenec Reference Candy, Belli and Bravenec2016) in burning plasma conditions. In both use cases, the thermal impurity ions (He, Ar, W) are taken to have the same profile shape as the electron density, while the energetic alpha particles are assumed to have a fixed classical distribution calculated by ONETWO, and the thermal deuterium and tritium ions are required to be equal in magnitude with profiles determined via quasi-neutrality. The argon is assumed to be fully ionized, while the tungsten is treated as a single species with an effective charge $Z = 50$![]() throughout the plasma and a concentration of $n_W/n_e = 1.5\times 10^{-5}$
throughout the plasma and a concentration of $n_W/n_e = 1.5\times 10^{-5}$![]() (as was assumed in the modelling of the SPARC PRD Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020; Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020). The assumed auxiliary electron heating and current drive profile is shown in figure 4(b), however, as noted above, no current is assumed to be driven in the UCR-P use case as it would be negligible relative to the inductive current. In the steady-state UCR-SS use case, the choice of $\eta _{{\rm CD}} = 0.4$
(as was assumed in the modelling of the SPARC PRD Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020; Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020). The assumed auxiliary electron heating and current drive profile is shown in figure 4(b), however, as noted above, no current is assumed to be driven in the UCR-P use case as it would be negligible relative to the inductive current. In the steady-state UCR-SS use case, the choice of $\eta _{{\rm CD}} = 0.4$![]() at $R_0 = 4 \,\mathrm {m}$
at $R_0 = 4 \,\mathrm {m}$![]() and $n_{20} = 2.0$
and $n_{20} = 2.0$![]() corresponds to $P_{{\rm CD}} = 20 I_{{\rm CD}}$
corresponds to $P_{{\rm CD}} = 20 I_{{\rm CD}}$![]() , i.e. 20 MW of power is required to drive 1 MA of current.
, i.e. 20 MW of power is required to drive 1 MA of current.

Figure 4. Predictions of (a) ion temperature $T_i$![]() , (b) electron temperature $T_e$
, (b) electron temperature $T_e$![]() , (c) electron density $n_e$
, (c) electron density $n_e$![]() and (d) safety factor $q$
and (d) safety factor $q$![]() for UCR-P (—, blue) and UCR-SS (—, red). Corresponding predictions with the density profiles held fixed at a specified shape are plotted as dashed lines (- - -). The profiles inside of $\rho _{{\rm tor}} = 0.9$
for UCR-P (—, blue) and UCR-SS (—, red). Corresponding predictions with the density profiles held fixed at a specified shape are plotted as dashed lines (- - -). The profiles inside of $\rho _{{\rm tor}} = 0.9$![]() are predicted using TGYRO, while outside that radius are held fixed using the assumed profiles of the starting EPED calculations.
are predicted using TGYRO, while outside that radius are held fixed using the assumed profiles of the starting EPED calculations.
Table 1. Summary of various global parameters and figures of merit for UCR-P and UCR-SS plasmas. While most terms and associated calculations are defined in the text, for comparison with other studies, we also include $q^* = (5 a^2 B_0/R_0 I_p)((1 + \kappa ^2)/2)$![]() . The various fractions are defined as $f_{{\rm DT}} = (n_D + n_T)/n_e$
. The various fractions are defined as $f_{{\rm DT}} = (n_D + n_T)/n_e$![]() , $f_{{\rm rad}} = P_{{\rm rad}}/(P_{{\rm rad}}+P_{{\rm sep}})$
, $f_{{\rm rad}} = P_{{\rm rad}}/(P_{{\rm rad}}+P_{{\rm sep}})$![]() , $f_{{\rm boot}} = I_{{\rm boot}}/I_p$
, $f_{{\rm boot}} = I_{{\rm boot}}/I_p$![]() , $f_{{\rm CD}} = I_{{\rm CD}}/I_p$
, $f_{{\rm CD}} = I_{{\rm CD}}/I_p$![]() and $f_G=\bar {n}/n_G$
and $f_G=\bar {n}/n_G$![]() , where $\bar {n}$
, where $\bar {n}$![]() is the line-averaged electron density.
is the line-averaged electron density.

The TGYRO calculations used here evaluated the fluxes from TGLF and NEO at seven radii uniformly distributed between $\rho _{{\rm tor}} = 0.3$![]() and 0.9, with normalized gradient scale lengths $R/L_X = -R\,{\rm d}(\ln X)/{\rm d}r_{{\rm min}}$
and 0.9, with normalized gradient scale lengths $R/L_X = -R\,{\rm d}(\ln X)/{\rm d}r_{{\rm min}}$![]() taken to vary linearly between these evaluation radii and equal to zero at $\rho _{{\rm tor}} = 0$
taken to vary linearly between these evaluation radii and equal to zero at $\rho _{{\rm tor}} = 0$![]() . Here, $r_{{\rm min}}$
. Here, $r_{{\rm min}}$![]() is the minor radius of a given flux surface as defined by Arbon, Candy & Belli (Reference Arbon, Candy and Belli2020), which is used to label flux surfaces in all GACODE (CGYRO, TGYRO, NEO and TGLF) calculations. While it is possible to extend the minimum radius in the TGYRO calculations further inward from at $\rho _{{\rm tor}} = 0.3$
is the minor radius of a given flux surface as defined by Arbon, Candy & Belli (Reference Arbon, Candy and Belli2020), which is used to label flux surfaces in all GACODE (CGYRO, TGYRO, NEO and TGLF) calculations. While it is possible to extend the minimum radius in the TGYRO calculations further inward from at $\rho _{{\rm tor}} = 0.3$![]() , we note that TGLF has not been well validated at such small radii, and furthermore, would correspond to moving inside the $q = 1$
, we note that TGLF has not been well validated at such small radii, and furthermore, would correspond to moving inside the $q = 1$![]() surface for UCR-P where sawtooth dynamics not considered in detail here likely play an important role. Nonetheless, the results of a resolution check shown in figure 5 illustrate that minimal differences in the predicted profiles (as well as the underlying gradient scale lengths) arise from extending inward to $\rho _{{\rm tor}} = 0.2$
surface for UCR-P where sawtooth dynamics not considered in detail here likely play an important role. Nonetheless, the results of a resolution check shown in figure 5 illustrate that minimal differences in the predicted profiles (as well as the underlying gradient scale lengths) arise from extending inward to $\rho _{{\rm tor}} = 0.2$![]() and doubling the number of locations where TGLF and NEO are evaluated.
and doubling the number of locations where TGLF and NEO are evaluated.

Figure 5. Predictions of (a) ion temperature $T_i$![]() , (b) electron temperature $T_e$
, (b) electron temperature $T_e$![]() and (c) electron density $n_e$
and (c) electron density $n_e$![]() for UCR-P (—, blue) and UCR-SS (—, red) with TGLF and NEO evaluated at seven radial locations evenly spaced in the range of $0.3 \le \rho _{{\rm tor}} \le 0.9$
for UCR-P (—, blue) and UCR-SS (—, red) with TGLF and NEO evaluated at seven radial locations evenly spaced in the range of $0.3 \le \rho _{{\rm tor}} \le 0.9$![]() , and at fifteen locations evenly spaced between $0.2 \le \rho _{{\rm tor}} \le 0.9$
, and at fifteen locations evenly spaced between $0.2 \le \rho _{{\rm tor}} \le 0.9$![]() (- - -).
(- - -).
2.3.1. Global energy confinement and performance
As shown in table 1, the scenarios are predicted to obtain thermal energy confinement times of the order of 1 s ($\tau _E = 1.4 \, \mathrm {s}$![]() for UCR-P, and 0.95 s for UCR-SS), corresponding to normalized confinement factors $H_{98(y,2)} = 0.82$
for UCR-P, and 0.95 s for UCR-SS), corresponding to normalized confinement factors $H_{98(y,2)} = 0.82$![]() and 1.2, respectively. In calculating $H_{98(y,2)}$
and 1.2, respectively. In calculating $H_{98(y,2)}$![]() , the loss power is taken to be equal to the total heating power $P_{{\rm heat}} = P_{{\rm aux}} + P_{\alpha }$
, the loss power is taken to be equal to the total heating power $P_{{\rm heat}} = P_{{\rm aux}} + P_{\alpha }$![]() used in calculating $\tau _E$
used in calculating $\tau _E$![]() , without any subtraction of radiation power, consistent with the database analysis used in determining the $\tau _{98(y,2)}$
, without any subtraction of radiation power, consistent with the database analysis used in determining the $\tau _{98(y,2)}$![]() scaling. While these $H_{98(y,2)}$
scaling. While these $H_{98(y,2)}$![]() values are consistent with many current-day experiments, they are somewhat lower than the current best-performing experiments (in terms of $H_{98(y,2)}$
values are consistent with many current-day experiments, they are somewhat lower than the current best-performing experiments (in terms of $H_{98(y,2)}$![]() values) or what is typically targeted or assumed for reactor scenarios i.e. roughly $H_{98(y,2)} > 1$
values) or what is typically targeted or assumed for reactor scenarios i.e. roughly $H_{98(y,2)} > 1$![]() for inductive scenarios and $H_{98(y,2)} \ge 1.5$
for inductive scenarios and $H_{98(y,2)} \ge 1.5$![]() for steady-state conditions.
for steady-state conditions.
The relatively low performance of these scenarios can be largely understood in terms of the guiding assumptions made in the scenario design. First, it is well known that the largest values of $H_{98(y,2)}$![]() achieved to date are almost exclusively obtained in plasmas with significant uni-directional NBI heating (i.e. all co- or counter-$I_p$
achieved to date are almost exclusively obtained in plasmas with significant uni-directional NBI heating (i.e. all co- or counter-$I_p$![]() ). NBI sources provide not only direct heating of the plasma ions, but also provide core fuelling and torque, all of which act to improve confinement. In contrast, the plasmas scenarios considered here are only heated by fusion products (which provide a roughly two-to-one ratio of electron to ion heating at these conditions), as well as supplementary RF power taken to only heat the electrons; no benefits are obtained from core fuelling and torque injection actuators as are available on current machines.
). NBI sources provide not only direct heating of the plasma ions, but also provide core fuelling and torque, all of which act to improve confinement. In contrast, the plasmas scenarios considered here are only heated by fusion products (which provide a roughly two-to-one ratio of electron to ion heating at these conditions), as well as supplementary RF power taken to only heat the electrons; no benefits are obtained from core fuelling and torque injection actuators as are available on current machines.
Second, turbulent transport and confinement is known to improve with increased plasma current $I_p$![]() (at fixed field and size), or equivalently decreased safety factor $q \propto 1/I_p$
(at fixed field and size), or equivalently decreased safety factor $q \propto 1/I_p$![]() . The targeting of relatively high edge safety factor values (compared with say $q_{95}$
. The targeting of relatively high edge safety factor values (compared with say $q_{95}$![]() values of 3–3.5 targeted in the ITER baseline scenario (ITER Physics Basis Editors et al. 1999; Shimada et al. Reference Shimada, Campbell, Mukhovatov, Fujiwara, Kirneva, Lackner, Nagami, Pustovitov, Uckan and Wesley2007) and SPARC primary reference discharge (PRD) Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020) for disruption risk mitigation therefore naturally leads to lower confinement in UCR-P than other inductive reactor scenarios. Breaking this tension between optimizing confinement via large $I_p$
values of 3–3.5 targeted in the ITER baseline scenario (ITER Physics Basis Editors et al. 1999; Shimada et al. Reference Shimada, Campbell, Mukhovatov, Fujiwara, Kirneva, Lackner, Nagami, Pustovitov, Uckan and Wesley2007) and SPARC primary reference discharge (PRD) Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020) for disruption risk mitigation therefore naturally leads to lower confinement in UCR-P than other inductive reactor scenarios. Breaking this tension between optimizing confinement via large $I_p$![]() and optimizing disruption risk via low $I_p$
and optimizing disruption risk via low $I_p$![]() is a key motivation for the advanced tokamak path (Kikuchi Reference Kikuchi1993; Luce Reference Luce2011) pursued in UCR-SS (which has both larger $H_{98(y,2)}$
is a key motivation for the advanced tokamak path (Kikuchi Reference Kikuchi1993; Luce Reference Luce2011) pursued in UCR-SS (which has both larger $H_{98(y,2)}$![]() and $q_{95}$
and $q_{95}$![]() than UCR-P). However, breaking this tension without relying on core fuelling or torque requires tailoring the safety factor in a significantly higher $\beta$
than UCR-P). However, breaking this tension without relying on core fuelling or torque requires tailoring the safety factor in a significantly higher $\beta$![]() plasma to stabilize the turbulence at large radius via large Shafranov shift (Bourdelle et al. Reference Bourdelle, Hoang, Litaudon, Roach and Tala2005). This shift also works in conjunction with strong plasma shaping to provide access to large pedestal pressure which the confinement can build upon. Ideally, this tailoring can be done with minimal application of expensive external current drive, such that the plasma naturally self-organizes into a stable state. The UCR-SS results show that this approach is possible, but for the assumptions and models used requires a larger fraction of the total current be external driven ($\sim$
plasma to stabilize the turbulence at large radius via large Shafranov shift (Bourdelle et al. Reference Bourdelle, Hoang, Litaudon, Roach and Tala2005). This shift also works in conjunction with strong plasma shaping to provide access to large pedestal pressure which the confinement can build upon. Ideally, this tailoring can be done with minimal application of expensive external current drive, such that the plasma naturally self-organizes into a stable state. The UCR-SS results show that this approach is possible, but for the assumptions and models used requires a larger fraction of the total current be external driven ($\sim$![]() 40 %) than what is typically desired ($\sim$
40 %) than what is typically desired ($\sim$![]() 10 %–20 % Buttery et al. Reference Buttery, Park, McClenaghan, Weisberg, Canik, Ferron, Garofalo, Holcomb, Leuer and Snyder2021), which in turn leads to significant recirculating power and lower overall efficiency. Because this solution depends so sensitively on not just global quantities such as stored energy but fine details of the density and temperature gradient profiles (which set the bootstrap current profile), these conclusions regarding current drive requirements are highly sensitive to the transport model used.
10 %–20 % Buttery et al. Reference Buttery, Park, McClenaghan, Weisberg, Canik, Ferron, Garofalo, Holcomb, Leuer and Snyder2021), which in turn leads to significant recirculating power and lower overall efficiency. Because this solution depends so sensitively on not just global quantities such as stored energy but fine details of the density and temperature gradient profiles (which set the bootstrap current profile), these conclusions regarding current drive requirements are highly sensitive to the transport model used.
In addition to the transport predictions, different models can give different predictions of the bootstrap current itself, as shown in figure 6. While the models converge beyond $\rho _{{\rm tor}} = 0.7\unicode{x2013} 0.8$![]() , the differences at smaller radii can have a non-trivial impact on the overall solution, as the bootstrap current itself scales directly with the safety factor and local kinetic gradients (also a function of the safety factor). Thus, truly self-consistent AT solutions, where the bootstrap current is the dominant term in determining the safety factor, are extremely sensitive and nonlinear functions of the external actuators are applied.
, the differences at smaller radii can have a non-trivial impact on the overall solution, as the bootstrap current itself scales directly with the safety factor and local kinetic gradients (also a function of the safety factor). Thus, truly self-consistent AT solutions, where the bootstrap current is the dominant term in determining the safety factor, are extremely sensitive and nonlinear functions of the external actuators are applied.

Figure 6. (a) Various components of the UCR-SS toroidal current profile, and (b) comparison of the toroidal bootstrap current density predicted by the original Sauter model (Sauter et al. Reference Sauter, Angioni and Lin-Liu1999, Reference Sauter, Angioni and Lin-Liu2002) (—), the Redl corrections to the Sauter model (Redl et al. Reference Redl, Angioni, Belli and Sauter2021) (— - —, grey) and direct calculation with the drift-kinetic code NEO (Belli & Candy Reference Belli and Candy2008, Reference Belli and Candy2012) (— —, green).
2.3.2. Core radiation and edge exhaust power characteristics
Another striking feature of the results is the very large radiative fraction and low conducted power through the separatrix $P_{{\rm sep}}$![]() for UCR-P, whereas UCR-SS has a much lower radiative fraction and higher value of $P_{{\rm sep}}$
for UCR-P, whereas UCR-SS has a much lower radiative fraction and higher value of $P_{{\rm sep}}$![]() . Each of these results presents challenges for core-edge integration. In UCR-P, the value of $P_{{\rm sep}}$
. Each of these results presents challenges for core-edge integration. In UCR-P, the value of $P_{{\rm sep}}$![]() predicted for the evolved density case is below the predicted L–H power threshold (calculated via the Martin scaling (Martin et al. Reference Martin and Takizuka2008) including isotope mass correction Behn et al. Reference Behn, Labit, Duval, Karpushov, Martin and Porte2014; Maggi et al. Reference Maggi, Delabie, Biewer, Groth, Hawkes, Lehnen, de la Luna, McCormick, Reux and Rimini2014) by nearly a factor of two and thus, at face value, is not self-consistent within the constraints listed in § 2.1. Ideally, one would lower the radiated power fraction to ensure the plasma remains in H-mode, while potentially simultaneously improving performance. However, UCR-SS is predicted to be well above the L–H transition threshold and thus potentially has headroom for further radiative cooling. While a detailed examination of the dependence on isotope mix is beyond the scope of this initial study, the results of a first step are shown in figure 7, as well as in table 1. Here, we have replaced the injected argon ($Z = 18$
predicted for the evolved density case is below the predicted L–H power threshold (calculated via the Martin scaling (Martin et al. Reference Martin and Takizuka2008) including isotope mass correction Behn et al. Reference Behn, Labit, Duval, Karpushov, Martin and Porte2014; Maggi et al. Reference Maggi, Delabie, Biewer, Groth, Hawkes, Lehnen, de la Luna, McCormick, Reux and Rimini2014) by nearly a factor of two and thus, at face value, is not self-consistent within the constraints listed in § 2.1. Ideally, one would lower the radiated power fraction to ensure the plasma remains in H-mode, while potentially simultaneously improving performance. However, UCR-SS is predicted to be well above the L–H transition threshold and thus potentially has headroom for further radiative cooling. While a detailed examination of the dependence on isotope mix is beyond the scope of this initial study, the results of a first step are shown in figure 7, as well as in table 1. Here, we have replaced the injected argon ($Z = 18$![]() ) with either neon ($Z = 10$
) with either neon ($Z = 10$![]() ) in UCR-P or krypton ($Z = 36$
) in UCR-P or krypton ($Z = 36$![]() ) in UCR-SS, while adjusting the DT fraction accordingly to keep the overall plasma $Z_{{\rm eff}}$
) in UCR-SS, while adjusting the DT fraction accordingly to keep the overall plasma $Z_{{\rm eff}}$![]() fixed (and thus the EPED pedestal pressure prediction as well). In this approach, virtually no change in the predicted profiles is found and only modest changes in parameters such as $Q_{{\rm fusion}}$
fixed (and thus the EPED pedestal pressure prediction as well). In this approach, virtually no change in the predicted profiles is found and only modest changes in parameters such as $Q_{{\rm fusion}}$![]() are observed. However, it should be noted that while the change to krypton modestly improves the net electric power generation for UCR-SS (219–233 MW), it also only reduces $P_{{\rm sep}}$
are observed. However, it should be noted that while the change to krypton modestly improves the net electric power generation for UCR-SS (219–233 MW), it also only reduces $P_{{\rm sep}}$![]() by 10 %, whereas changing to neon increases $P_{{\rm sep}}$
by 10 %, whereas changing to neon increases $P_{{\rm sep}}$![]() by 50 % for UCR-P but drops the predicted net power from 218 MW to 185 MW, below the 200 MW target established. One could imagine lowering the target $Z_{{\rm eff}}$
by 50 % for UCR-P but drops the predicted net power from 218 MW to 185 MW, below the 200 MW target established. One could imagine lowering the target $Z_{{\rm eff}}$![]() for UCR-P (or raising it for UCR-SS) to gain further headroom, but EPED typically predicts increasing pedestal pressure with increased $Z_{{\rm eff}}$
for UCR-P (or raising it for UCR-SS) to gain further headroom, but EPED typically predicts increasing pedestal pressure with increased $Z_{{\rm eff}}$![]() . Thus, lowering $Z_{{\rm eff}}$
. Thus, lowering $Z_{{\rm eff}}$![]() could enable less radiation, but is also likely to lead to less fusion power generation, while raising $Z_{{\rm eff}}$
could enable less radiation, but is also likely to lead to less fusion power generation, while raising $Z_{{\rm eff}}$![]() could increase both radiated power and fusion power. Therefore, for both UCR-P and UCR-SS, one would need to carefully assess the trade-off in radiated power optimization versus changes to fusion power generated to determine the net benefit.
could increase both radiated power and fusion power. Therefore, for both UCR-P and UCR-SS, one would need to carefully assess the trade-off in radiated power optimization versus changes to fusion power generated to determine the net benefit.

Figure 7. Comparison of predicted (a) ion temperature $T_i$![]() , (b) electron temperature $T_e$
, (b) electron temperature $T_e$![]() and (c) electron density $n_e$
and (c) electron density $n_e$![]() for UCR-P (—, blue) and UCR-SS (—, red) with argon as an injected edge radiator versus neon in UCR-P (— —, cyan) or krypton in UCR-SS (— —, orange). The DT fraction in the plasma is self-consistently adjusted with the change in injected radiative gas to maintain $Z_{{\rm eff}}$
for UCR-P (—, blue) and UCR-SS (—, red) with argon as an injected edge radiator versus neon in UCR-P (— —, cyan) or krypton in UCR-SS (— —, orange). The DT fraction in the plasma is self-consistently adjusted with the change in injected radiative gas to maintain $Z_{{\rm eff}}$![]() .
.
In considering the question of proximity to the L–H threshold, it should be noted that there remains significant uncertainties in the underlying physics and scaling of the threshold power, as well as possible hysteresis in H-mode entrance and exit powers. As an example, experiments in JET with a metallic ITER-like wall found a further 30 % reduction in the threshold power (Maggi et al. Reference Maggi, Delabie, Biewer, Groth, Hawkes, Lehnen, de la Luna, McCormick, Reux and Rimini2014). More broadly, the predicted results are of course quite sensitive to the pedestal pressure and confinement could therefore be improved with even minor changes or additional optimization. For instance, simply raising $T_{{\rm ped}}$![]() by 14 % from 3.5 to 4 keV in UCR-P is sufficient to raise $P_{{\rm sep}}$
by 14 % from 3.5 to 4 keV in UCR-P is sufficient to raise $P_{{\rm sep}}$![]() to 80 MW, nearly equal to the $P_{{\rm LH}}$
to 80 MW, nearly equal to the $P_{{\rm LH}}$![]() ; modest reductions in radiative impurities or especially the $\mathrm {He}^4$
; modest reductions in radiative impurities or especially the $\mathrm {He}^4$![]() ash can raise it further still. This increase in $T_{{\rm ped}}$
ash can raise it further still. This increase in $T_{{\rm ped}}$![]() could be obtained by increasing plasma triangularity from 0.5 to 0.6 (equal to what is assumed by Buttery et al. Reference Buttery, Park, McClenaghan, Weisberg, Canik, Ferron, Garofalo, Holcomb, Leuer and Snyder2021), and is also within the 20 % uncertainty of the EPED prediction itself. Of course, the converse is true as well: even modest reduction of $T_{{\rm ped}}$
could be obtained by increasing plasma triangularity from 0.5 to 0.6 (equal to what is assumed by Buttery et al. Reference Buttery, Park, McClenaghan, Weisberg, Canik, Ferron, Garofalo, Holcomb, Leuer and Snyder2021), and is also within the 20 % uncertainty of the EPED prediction itself. Of course, the converse is true as well: even modest reduction of $T_{{\rm ped}}$![]() would likely eliminate H-mode access and necessitate development of a new design point. It should also be noted that the density and temperature profiles are assumed fixed with $T_i = T_e$
would likely eliminate H-mode access and necessitate development of a new design point. It should also be noted that the density and temperature profiles are assumed fixed with $T_i = T_e$![]() beyond $\rho _{{\rm tor}} = 0.9$
beyond $\rho _{{\rm tor}} = 0.9$![]() , whereas in reality, there would be some amount of separation due to differences in transport processes in the pedestal and scrape-off layer, which would in turn impact predictions of the radiation and power flowing across the separatrix. Another key assumption of this modelling is that the relative concentrations of different impurity ion species are fixed at rather arbitrary levels, as a physics-based capability for predicting these concentrations remains lacking. Thus, these pedestal and edge values should be treated as suggestive rather than definitive conclusions, and like the core parameters, a starting point for more detailed future studies of pedestal and edge transport.
, whereas in reality, there would be some amount of separation due to differences in transport processes in the pedestal and scrape-off layer, which would in turn impact predictions of the radiation and power flowing across the separatrix. Another key assumption of this modelling is that the relative concentrations of different impurity ion species are fixed at rather arbitrary levels, as a physics-based capability for predicting these concentrations remains lacking. Thus, these pedestal and edge values should be treated as suggestive rather than definitive conclusions, and like the core parameters, a starting point for more detailed future studies of pedestal and edge transport.
As the calculations used in this workflow do not extend beyond the last closed flux surface (LCFS) of the plasma, little can be said regarding transport and plasma conditions in the scrape-off layer, which must be better characterized and understood to accurately quantify the challenge posed by the ITEP gap. Nonetheless, a few key quantities can be projected using the information available and various scaling laws from the literature. First, one can use the well-known Eich scaling (Eich et al. Reference Eich, Leonard, Pitts, Fundamenski, Goldston, Gray, Herrmann, Kirk, Kallenbach and Kardaun2013) for the parallel scrape-off layer heat flux width $\lambda _q = 1.35 P_{{\rm sep}}^{-0.02} R^{0.04}(a/R)^{0.42} {B_{\theta,{\rm mid}}}^{-0.92}$![]() to estimate widths of 0.43 mm in UCR-P and 0.49 mm in UCR-SS. These widths correspond to midplane parallel heat fluxes $q_{\|} = P_{{\rm sep}} B/(2 {\rm \pi}R \lambda _q B_{\theta }) \sim 16.5 \,\mathrm {GW}\,\mathrm {m}^{-2}$
to estimate widths of 0.43 mm in UCR-P and 0.49 mm in UCR-SS. These widths correspond to midplane parallel heat fluxes $q_{\|} = P_{{\rm sep}} B/(2 {\rm \pi}R \lambda _q B_{\theta }) \sim 16.5 \,\mathrm {GW}\,\mathrm {m}^{-2}$![]() in UCR-P and $90 \, \mathrm {GW}\,\mathrm {m}^{-2}$
in UCR-P and $90 \, \mathrm {GW}\,\mathrm {m}^{-2}$![]() in UCR-SS. Since $\lambda _q$
in UCR-SS. Since $\lambda _q$![]() effectively varies inversely with $B_{\theta }$
effectively varies inversely with $B_{\theta }$![]() , the simpler metric of $Q_{\|} = P_{{\rm sep}}B/R$
, the simpler metric of $Q_{\|} = P_{{\rm sep}}B/R$![]() is also sometimes used. For UCR-P and UCR-SS, one has $Q_{\|} \sim 90$
is also sometimes used. For UCR-P and UCR-SS, one has $Q_{\|} \sim 90$![]() and 500 MW T m$^{-1}$
and 500 MW T m$^{-1}$![]() , respectively. However, these calculations used the predicted $P_{{\rm sep}}$
, respectively. However, these calculations used the predicted $P_{{\rm sep}}$![]() values shown in table 1, which as noted above are either well below or above the estimated L–H threshold value. Given that both use cases are projected to have $P_{{\rm LH}} \sim 80 \,\mathrm {MW}$
values shown in table 1, which as noted above are either well below or above the estimated L–H threshold value. Given that both use cases are projected to have $P_{{\rm LH}} \sim 80 \,\mathrm {MW}$![]() , that value may be a more meaningful choice for estimating exhaust power. Assuming $P_{{\rm sep}} = P_{{\rm LH}} = 80 \,\mathrm {MW}$
, that value may be a more meaningful choice for estimating exhaust power. Assuming $P_{{\rm sep}} = P_{{\rm LH}} = 80 \,\mathrm {MW}$![]() yields $q_{\|} \sim 30 \, \mathrm {GW}\,\mathrm {m}^{-2}$
yields $q_{\|} \sim 30 \, \mathrm {GW}\,\mathrm {m}^{-2}$![]() and $Q_{\|} = 160 \,\mathrm {MW}\,\mathrm {T}\,\mathrm {m}^{-1}$
and $Q_{\|} = 160 \,\mathrm {MW}\,\mathrm {T}\,\mathrm {m}^{-1}$![]() . Regardless of the specific choices, these values are significantly larger than current-day facilities, but comparable to what is expected in various proposed burning plasma facilities and FPPs. Like those facilities, one would require a combination of additional scrape-off layer volumetric radiation and detachment (Leonard Reference Leonard2018) to reduce the heat fluxes actually impinging on solid plasma-facing components in the divertor to tolerable levels. Determining this exhaust solution for an actual compact reactor requires modelling and design capabilities well beyond what is considered here, as well as better understanding of edge transport processes such as turbulent broadening of the heat flux (Eich et al. Reference Eich, Manz, Goldston, Hennequin, David, Faitsch, Kurzan, Sieglin and Wolfrum2020; Li et al. Reference Li, Xu, Goldston, Sun and Wang2020; Chang et al. Reference Chang, Ku, Hager, Churchill, Hughes, Köchl, Loarte, Parail and Pitts2021; Mandell et al. Reference Mandell, Hammett, Hakim and Francisquez2022).
. Regardless of the specific choices, these values are significantly larger than current-day facilities, but comparable to what is expected in various proposed burning plasma facilities and FPPs. Like those facilities, one would require a combination of additional scrape-off layer volumetric radiation and detachment (Leonard Reference Leonard2018) to reduce the heat fluxes actually impinging on solid plasma-facing components in the divertor to tolerable levels. Determining this exhaust solution for an actual compact reactor requires modelling and design capabilities well beyond what is considered here, as well as better understanding of edge transport processes such as turbulent broadening of the heat flux (Eich et al. Reference Eich, Manz, Goldston, Hennequin, David, Faitsch, Kurzan, Sieglin and Wolfrum2020; Li et al. Reference Li, Xu, Goldston, Sun and Wang2020; Chang et al. Reference Chang, Ku, Hager, Churchill, Hughes, Köchl, Loarte, Parail and Pitts2021; Mandell et al. Reference Mandell, Hammett, Hakim and Francisquez2022).
2.3.3. Macroscopic stability
Beyond the transport and confinement properties considered so far, it is also essential to ensure that the scenario equilibrium is macroscopically stable, for which the most relevant parameters are the edge safety factor $q_{95}$![]() and normalized plasma pressure $\beta _{N}$
and normalized plasma pressure $\beta _{N}$![]() . All of the plasmas considered here have $q_{95} \ge 4.7$
. All of the plasmas considered here have $q_{95} \ge 4.7$![]() and thus would generally be expected to be reasonably stable against external kink modes (Wesson Reference Wesson1978). Additionally, UCR-P has a relatively moderate $\beta _{N} = 1.7$
and thus would generally be expected to be reasonably stable against external kink modes (Wesson Reference Wesson1978). Additionally, UCR-P has a relatively moderate $\beta _{N} = 1.7$![]() (similar to the ITER baseline scenario), below the Troyon no-wall limit of 2.8. To account for the impact of current profile peakedness on the global stability limit, a more refined calculation suggests instability should be expected when $\beta _{N} > 4l_i$
(similar to the ITER baseline scenario), below the Troyon no-wall limit of 2.8. To account for the impact of current profile peakedness on the global stability limit, a more refined calculation suggests instability should be expected when $\beta _{N} > 4l_i$![]() (Turnbull et al. Reference Turnbull, Snyder, Brennan, Chu and Lao2005), where $l_i$
(Turnbull et al. Reference Turnbull, Snyder, Brennan, Chu and Lao2005), where $l_i$![]() is the normalized plasma inductance calculated with the $l_i(3) = 2V\left \langle B_{\theta }^2\right \rangle /[(\mu _0 I_p)^2 R]$
is the normalized plasma inductance calculated with the $l_i(3) = 2V\left \langle B_{\theta }^2\right \rangle /[(\mu _0 I_p)^2 R]$![]() definition used in the ITER design and physics basis (Jackson et al. Reference Jackson, Casper, Luce, Humphreys, Ferron, Hyatt, Lazarus, Moyer, Petrie and Rudakov2008). The strong peaking of the Ohmic on-axis current in UCR-P gives $l_i = 0.77$
definition used in the ITER design and physics basis (Jackson et al. Reference Jackson, Casper, Luce, Humphreys, Ferron, Hyatt, Lazarus, Moyer, Petrie and Rudakov2008). The strong peaking of the Ohmic on-axis current in UCR-P gives $l_i = 0.77$![]() , such that $\beta _{N}/4 l_i = 0.56$
, such that $\beta _{N}/4 l_i = 0.56$![]() , comfortably below the estimated instability threshold. However, the peaking of the Ohmic current in UCR-P will drive sawteeth with an inversion radius $\rho _{{\rm inv}} \sim 0.3$
, comfortably below the estimated instability threshold. However, the peaking of the Ohmic current in UCR-P will drive sawteeth with an inversion radius $\rho _{{\rm inv}} \sim 0.3$![]() .
.
Perhaps more concerning is the presence of low-order rational surfaces where neoclassical tearing modes (NTMs) (LaHaye et al. Reference LaHaye, Prater, Buttery, Hayashi, Isayama, Maraschek, Urso and Zohm2006) destabilized by the sawteeth and/or ELMs can form, significantly degrading performance and perhaps even driving disruptions (de Vries et al. Reference de Vries, Johnson, Alper, Buratti, Hender, Koslowski and Riccardo2011; Sweeney et al. Reference Sweeney, Choi, Haye, Mao, Olofsson and Volpe2016). Devices such as ITER aim to mitigate NTM impacts via the application of localized electron cyclotron resonance current drive. Although the current drive details are not analysed in detail here, a preliminary analysis suggests that UCR-P could support at least some NTM suppression without undue impacts on fusion gain, stability or $P_{{\rm electric}}$![]() . The ‘rule of thumb’ for NTM stabilization is that enough external current must be driven to at least replace the bootstrap current at the relevant rational surface (Poli et al. Reference Poli, Fredrickson, Henderson, Kim, Bertelli, Poli, Farina and Figini2017). For UCR-P, this criterion would require driving $0.22 \, \mathrm {MA}\,\mathrm {m}^{-2}$
. The ‘rule of thumb’ for NTM stabilization is that enough external current must be driven to at least replace the bootstrap current at the relevant rational surface (Poli et al. Reference Poli, Fredrickson, Henderson, Kim, Bertelli, Poli, Farina and Figini2017). For UCR-P, this criterion would require driving $0.22 \, \mathrm {MA}\,\mathrm {m}^{-2}$![]() on the $q = 2$
on the $q = 2$![]() surface at $\rho _{{\rm tor}} = 0.7$
surface at $\rho _{{\rm tor}} = 0.7$![]() , which we assume to be the highest priority for stabilization. Assuming the same $\eta _{{\rm CD}} = 0.4$
, which we assume to be the highest priority for stabilization. Assuming the same $\eta _{{\rm CD}} = 0.4$![]() and a similarly localized deposition as the off-axis drive in UCR-SS, the $\sim$
and a similarly localized deposition as the off-axis drive in UCR-SS, the $\sim$![]() 25 % higher density of UCR-P translates into a requirement of $P_{{\rm CD}} = 18 \,\mathrm {MW}$
25 % higher density of UCR-P translates into a requirement of $P_{{\rm CD}} = 18 \,\mathrm {MW}$![]() . If this power was added to the 30 MW of central heating already present, it would increase the total injected power by 60 % and also incur a substantial recirculating power penalty of 41 MW (via (2.1)). However, because UCR-P is already strongly burning ($Q_{{\rm fusion}} = 27$
. If this power was added to the 30 MW of central heating already present, it would increase the total injected power by 60 % and also incur a substantial recirculating power penalty of 41 MW (via (2.1)). However, because UCR-P is already strongly burning ($Q_{{\rm fusion}} = 27$![]() ) and does not depend upon off-axis current drive for confinement, we find that the required power could be obtained by simply reducing the core power heating to 12 MW, without any significant impact on profile shape, confinement or total current profile. In essence, the strong self-heating and dominant inductive current of UCR-P makes it quite insensitive to changes in the heating deposition profile.
) and does not depend upon off-axis current drive for confinement, we find that the required power could be obtained by simply reducing the core power heating to 12 MW, without any significant impact on profile shape, confinement or total current profile. In essence, the strong self-heating and dominant inductive current of UCR-P makes it quite insensitive to changes in the heating deposition profile.
In contrast to UCR-P, the larger safety factor in UCR-SS and the corresponding elimination of low-order surfaces (particularly the 1/1 and 3/2 surfaces) helps mitigate against the NTM challenge somewhat, although the $q = 2$![]() surface is still present in the plasma (albeit much closer to the core). However, the broader current profile of UCR-SS leads to a slightly lower plasma inductance $l_i = 0.5$
surface is still present in the plasma (albeit much closer to the core). However, the broader current profile of UCR-SS leads to a slightly lower plasma inductance $l_i = 0.5$![]() , such that its normalized plasma pressure $\beta _{N} = 3.3$
, such that its normalized plasma pressure $\beta _{N} = 3.3$![]() is well above both estimates of the no-wall limit (either 2.8 or $4 l_i = 2.0$
is well above both estimates of the no-wall limit (either 2.8 or $4 l_i = 2.0$![]() ). A more detailed stability analysis of UCR-SS with the GATO code (Bernard, Helton & Moore Reference Bernard, Helton and Moore1981) finds that the no-wall equilibrium is indeed unstable to a toroidal mode number $n = 1$
). A more detailed stability analysis of UCR-SS with the GATO code (Bernard, Helton & Moore Reference Bernard, Helton and Moore1981) finds that the no-wall equilibrium is indeed unstable to a toroidal mode number $n = 1$![]() perturbation as might be expected (figure 8), but that this mode can be stabilized by an ideal conducting conformal wall at $a_{{\rm wall}} \le 1.25 a_{{\rm plasma}}$
perturbation as might be expected (figure 8), but that this mode can be stabilized by an ideal conducting conformal wall at $a_{{\rm wall}} \le 1.25 a_{{\rm plasma}}$![]() (i.e. if the wall is placed with 35 cm of the separatrix). Thus, it appears that from an ideal MHD stability standpoint, both scenarios are nominally acceptable at the first pass. Nonetheless, their robustness to NTM formation, as well as resistive wall modes, remains uncertain, and we note that absent of any rotation (as is assumed here), these modes have significant potential to degrade or disrupt the plasma via wall-locking (Nave & Wesson Reference Nave and Wesson1990). Moreover, the criteria outlined above can at best be considered rough guidelines, especially for non-circular diverted plasmas, and more detailed assessments of MHD stability would be appropriate for further optimization studies of UCR plasmas, especially for $n > 1$
(i.e. if the wall is placed with 35 cm of the separatrix). Thus, it appears that from an ideal MHD stability standpoint, both scenarios are nominally acceptable at the first pass. Nonetheless, their robustness to NTM formation, as well as resistive wall modes, remains uncertain, and we note that absent of any rotation (as is assumed here), these modes have significant potential to degrade or disrupt the plasma via wall-locking (Nave & Wesson Reference Nave and Wesson1990). Moreover, the criteria outlined above can at best be considered rough guidelines, especially for non-circular diverted plasmas, and more detailed assessments of MHD stability would be appropriate for further optimization studies of UCR plasmas, especially for $n > 1$![]() modes which have not been considered here. Given that the EPED code was used to provide the pedestal height, examining the potential impacts of suppressing (or at least mitigating) intermediate-$n$
modes which have not been considered here. Given that the EPED code was used to provide the pedestal height, examining the potential impacts of suppressing (or at least mitigating) intermediate-$n$![]() ELMs on the pedestal height and width would be particularly important.
ELMs on the pedestal height and width would be particularly important.

Figure 8. GATO predictions of toroidal mode number $n = 1$![]() instability in UCR-SS, showing (a) that the instability is suppressed by a conformal wall located within 25 % of the plasma minor radius and (b) the amplitudes of the $n = 1$
instability in UCR-SS, showing (a) that the instability is suppressed by a conformal wall located within 25 % of the plasma minor radius and (b) the amplitudes of the $n = 1$![]() no-wall eigenmode radial displacement poloidal harmonics $\xi _m$
no-wall eigenmode radial displacement poloidal harmonics $\xi _m$![]() , which are dominated by poloidal mode numbers $m = 2 \unicode{x2013} 4$
, which are dominated by poloidal mode numbers $m = 2 \unicode{x2013} 4$![]() .
.
A final stability concern for burning plasmas is the possibility of energetic particle-driven Alfvén eigenmodes (AEs) (Heidbrink Reference Heidbrink2008; Lauber Reference Lauber2015). In particular, it is possible that the energetic alpha particles born in the fusion reactions can resonantly destabilize the otherwise stable AEs, which will in turn rapidly redistribute the alpha particles (and their associated heating) in the plasma, or even eject them out of the plasma and into the first wall. As shown in figure 9(a), the predicted alpha densities are quite small relative to the electrons (less than 2 %), due to the relatively high absolute plasma density leading to a fast equilibration of the alpha population. However, as shown in figure 9(b), the effective temperature of the hot alphas is so much larger than the background thermal temperatures that they provide approximately 20 % of the on-axis pressure, and thus contribute to both the overall magnetic equilibrium and stabilization of turbulence via increased Shafranov shift. While full and self-consistent predictions of AE-driven alpha transport remain an area of significant current research (Bass & Waltz Reference Bass and Waltz2017; Liu et al. Reference Liu, Wei, Lin, Brochard, Choi, Heidbrink, Nicolau and McKee2022; Zou et al. Reference Zou, Chan, Van Zeeland, Heidbrink, Todo, Chen, Wang and Chen2022), one way to begin assessing its possible impact is to examine the stability of the predicted alpha density profile to the onset of such modes. Figures 9(c) and 9(d) show the alpha density gradient profiles for UCR-P and UCR-SS, respectively.

Figure 9. Energetic alpha particle (a) density $n_{\alpha }/n_e$![]() and (b) pressure $p_{\alpha }/p_{{\rm tot}}$
and (b) pressure $p_{\alpha }/p_{{\rm tot}}$![]() fractions for UCR-P (—, blue) and UCR-SS (—, red), calculated in ONETWO assuming purely classical slowing-down collisions. These classical density gradient profiles for (c) UCR-P and (d) UCR-SS are compared with the estimated threshold ${\rm d}n_{\alpha }/{\rm d}r_{{\rm min}}$
fractions for UCR-P (—, blue) and UCR-SS (—, red), calculated in ONETWO assuming purely classical slowing-down collisions. These classical density gradient profiles for (c) UCR-P and (d) UCR-SS are compared with the estimated threshold ${\rm d}n_{\alpha }/{\rm d}r_{{\rm min}}$![]() values for a $k_y \rho _{{\rm sD}} = 0.05$
values for a $k_y \rho _{{\rm sD}} = 0.05$![]() Alfvén eigenmode ($k_y \rho _{\alpha } = 0.2\unicode{x2013}0.4$
Alfvén eigenmode ($k_y \rho _{\alpha } = 0.2\unicode{x2013}0.4$![]() ) to be driven unstable (— $\blacklozenge$
) to be driven unstable (— $\blacklozenge$![]() —). The threshold is estimated using local linear gyrokinetic simulations in which ${\rm d}n_{\alpha }/{\rm d}r_{{\rm min}}$
—). The threshold is estimated using local linear gyrokinetic simulations in which ${\rm d}n_{\alpha }/{\rm d}r_{{\rm min}}$![]() is scanned while holding all other parameters fixed (although the pressure gradient contributions to the magnetic drift frequency are varied self-consistently).
is scanned while holding all other parameters fixed (although the pressure gradient contributions to the magnetic drift frequency are varied self-consistently).
To begin examining their stability to alpha-driven AEs, local linear stability gyrokinetic calculations performed with the CGYRO code were made at $\rho _{{\rm tor}} = [0.1, 0.2, \ldots 0.8 ]$![]() . These calculations quantified how the growth rates of modes with binormal wavenumber $k_y\rho _{{\rm sD}} = 0.05$
. These calculations quantified how the growth rates of modes with binormal wavenumber $k_y\rho _{{\rm sD}} = 0.05$![]() (equivalent to $k_y \rho _{\alpha }= 0.2\unicode{x2013}0.4$
(equivalent to $k_y \rho _{\alpha }= 0.2\unicode{x2013}0.4$![]() ) varied with local alpha density gradient scale length. Here, $k_y = nq/r_{{\rm min}} \sim k_{\theta }$
) varied with local alpha density gradient scale length. Here, $k_y = nq/r_{{\rm min}} \sim k_{\theta }$![]() is the local binormal wavenumber associated with toroidal mode number $n$
is the local binormal wavenumber associated with toroidal mode number $n$![]() , and $\rho _{{\rm sD}} = c_{{\rm sD}}/\varOmega _{cD}$
, and $\rho _{{\rm sD}} = c_{{\rm sD}}/\varOmega _{cD}$![]() are the deuterium thermal sound gyroradius evaluated using $T_e$
are the deuterium thermal sound gyroradius evaluated using $T_e$![]() instead of $T_i$
instead of $T_i$![]() . This wavelength was predicted to be unstable in the middle of UCR-P, $0.4 \le \rho _{{\rm tor}} \le 0.6$
. This wavelength was predicted to be unstable in the middle of UCR-P, $0.4 \le \rho _{{\rm tor}} \le 0.6$![]() . A much broader region of UCR-SS ($0.2 \le \rho _{{\rm tor}} \le 0.7$
. A much broader region of UCR-SS ($0.2 \le \rho _{{\rm tor}} \le 0.7$![]() ) was predicted to be unstable when the local alpha density gradient was roughly half the predicted value or larger, suggesting that more significant alpha-driven AEs may be present in this scenario. Experimentally, fast-ion driven AEs have been observed in a range of current-day advanced tokamak and high $\beta _p$
) was predicted to be unstable when the local alpha density gradient was roughly half the predicted value or larger, suggesting that more significant alpha-driven AEs may be present in this scenario. Experimentally, fast-ion driven AEs have been observed in a range of current-day advanced tokamak and high $\beta _p$![]() discharges (Heidbrink et al. Reference Heidbrink, Ferron, Holcomb, Zeeland, Chen, Collins, Garofalo, Gong, Grierson and Podest2014; Varela et al. Reference Varela, Spong, Garcia, Huang, Murakami, Garofalo, Qian, Holcomb, Hyatt and Ferron2018; Jian et al. Reference Jian, Holland, Bass, Ding, Du, Chan, Garofalo, Grierson, McClenaghan and Yu2022b). While these modes typically have very low toroidal mode numbers ($n \sim 1-5$
discharges (Heidbrink et al. Reference Heidbrink, Ferron, Holcomb, Zeeland, Chen, Collins, Garofalo, Gong, Grierson and Podest2014; Varela et al. Reference Varela, Spong, Garcia, Huang, Murakami, Garofalo, Qian, Holcomb, Hyatt and Ferron2018; Jian et al. Reference Jian, Holland, Bass, Ding, Du, Chan, Garofalo, Grierson, McClenaghan and Yu2022b). While these modes typically have very low toroidal mode numbers ($n \sim 1-5$![]() ) in the current day discharges, they would be roughly twice as large ($n \sim 10$
) in the current day discharges, they would be roughly twice as large ($n \sim 10$![]() ) in UCR-SS. Whether such higher-$n$
) in UCR-SS. Whether such higher-$n$![]() modes would exhibit similar dynamics as the low-$n$
modes would exhibit similar dynamics as the low-$n$![]() AEs of current day discharges, especially if there is a spectrum of such higher-$n$
AEs of current day discharges, especially if there is a spectrum of such higher-$n$![]() AEs unstable, remains to be determined.
AEs unstable, remains to be determined.
3. Core transport
In this section, we examine the transport characteristics of UCR-P and UCR-SS in greater detail. We focus only on the core transport (defined as inside of $\rho _{{\rm tor}} = 0.9$![]() where transport predictions were made using TGYRO), as no modelling of the profiles or transport at larger radii was performed beyond the EPED pedestal profile calculation and scrape-off layer heat flux width scaling calculations presented in § 2.3. Some implications of the core transport results presented here for future pedestal and scrape-off layer transport studies are discussed in § 4.
where transport predictions were made using TGYRO), as no modelling of the profiles or transport at larger radii was performed beyond the EPED pedestal profile calculation and scrape-off layer heat flux width scaling calculations presented in § 2.3. Some implications of the core transport results presented here for future pedestal and scrape-off layer transport studies are discussed in § 4.
3.1. Basic transport characteristics
We begin the characterization of the core transport by examining various components of the total power flows, which correspond to the various elements of the steady-state flux-surface averaged energy transport equations TGYRO solves (with $V' = {\rm d}V/{\rm d}r_{{\rm min}}$![]() approximately equivalent to the surface area of each flux surface):
approximately equivalent to the surface area of each flux surface):
Figure 10 shows the various components of (3.1) and (3.2), in terms of power flows equal to cumulative volume integrals of the corresponding source terms. Thus, for example, $P_{{\rm aux}}(x)$![]() quantifies the total amount of auxiliary heating inside $\rho _{{\rm tor}} = x$
quantifies the total amount of auxiliary heating inside $\rho _{{\rm tor}} = x$![]() , i.e. $P_{{\rm aux}}(x) = V'(x)Q_{{\rm aux}}(x)= \int _0^x \,{\rm d}r V'(r) S_{{\rm aux}}(r)$
, i.e. $P_{{\rm aux}}(x) = V'(x)Q_{{\rm aux}}(x)= \int _0^x \,{\rm d}r V'(r) S_{{\rm aux}}(r)$![]() . Ohmic heating is formally included as an auxiliary electron heating source but is negligible for these plasmas, while all radiation losses (due to cyclotron emission, bremsstrahlung and line radiation) are taken from the electrons. The line radiation is calculated in the same fashion as in the AURORA code (Sciortino et al. Reference Sciortino, Odstrčil, Cavallaro, Smith, Meneghini, Reksoatmodjo, Linder, Lore, Howard and Marmar2021), including use of data from OPEN-ADAS (https://open.adas.ac.uk/) (Summers et al. Reference Summers, Dickson, O'Mullane, Badnell, Whiteford, Brooks, Lang, Loch and Griffin2006) and Pütterich et al. (Reference Pütterich, Fable, Dux, O‘Mullane, Neu and Siccinio2019). As would be expected for burning plasmas, heating of the thermal ions and electrons via collisions with the energetic alpha particles is the dominant energy source. More interesting is the fact that a significant fraction of the net power flow is carried by the ions in both cases, even though the majority of the heating (roughly two-thirds of the alpha heating and all auxiliary heating) is to the electrons. This difference arises from two processes. First, radiative losses which cool the electrons are quite significant in both scenarios: roughly equal to the auxiliary heating power in UCR-SS, and nearly five times as much as the auxiliary heating in UCR-P. Second, although most heating (even after subtracting the radiation) is to the electrons which pushes the core plasma to hotter electrons than ions, the plasmas remain sufficiently coupled that significant collisional exchange (of the order of 20–40 MW) from the electrons to the ions occurs. Given that both radiative losses and collisional coupling scale directly with plasma density, one might view this result as a trivial consequence of operating at relatively high density (compared with e.g. Greenwald or $\beta$
. Ohmic heating is formally included as an auxiliary electron heating source but is negligible for these plasmas, while all radiation losses (due to cyclotron emission, bremsstrahlung and line radiation) are taken from the electrons. The line radiation is calculated in the same fashion as in the AURORA code (Sciortino et al. Reference Sciortino, Odstrčil, Cavallaro, Smith, Meneghini, Reksoatmodjo, Linder, Lore, Howard and Marmar2021), including use of data from OPEN-ADAS (https://open.adas.ac.uk/) (Summers et al. Reference Summers, Dickson, O'Mullane, Badnell, Whiteford, Brooks, Lang, Loch and Griffin2006) and Pütterich et al. (Reference Pütterich, Fable, Dux, O‘Mullane, Neu and Siccinio2019). As would be expected for burning plasmas, heating of the thermal ions and electrons via collisions with the energetic alpha particles is the dominant energy source. More interesting is the fact that a significant fraction of the net power flow is carried by the ions in both cases, even though the majority of the heating (roughly two-thirds of the alpha heating and all auxiliary heating) is to the electrons. This difference arises from two processes. First, radiative losses which cool the electrons are quite significant in both scenarios: roughly equal to the auxiliary heating power in UCR-SS, and nearly five times as much as the auxiliary heating in UCR-P. Second, although most heating (even after subtracting the radiation) is to the electrons which pushes the core plasma to hotter electrons than ions, the plasmas remain sufficiently coupled that significant collisional exchange (of the order of 20–40 MW) from the electrons to the ions occurs. Given that both radiative losses and collisional coupling scale directly with plasma density, one might view this result as a trivial consequence of operating at relatively high density (compared with e.g. Greenwald or $\beta$![]() limits). However, it will be shown in § 4 that a similar conclusion holds for ITER and SPARC plasmas targeting lower Greenwald fractions and $\beta$
limits). However, it will be shown in § 4 that a similar conclusion holds for ITER and SPARC plasmas targeting lower Greenwald fractions and $\beta$![]() values, and the implications for reactor plasmas are discussed there.
values, and the implications for reactor plasmas are discussed there.

Figure 10. Comparison of net power flows (thick lines) and their various contributions for (a) UCR-P and (b) UCR-SS, as defined in (3.1)–(3.2). Note that the exchange term $P_{{\rm exchange}}$![]() is defined as positive when energy is flowing from electrons to ions. The shaded bands indicate the pedestal region where profile shapes are assumed rather than predicted, as well as the deep core region where inverse gradient scale lengths are taken to linearly decrease to zero at $\rho _{{\rm tor}} = 0$
is defined as positive when energy is flowing from electrons to ions. The shaded bands indicate the pedestal region where profile shapes are assumed rather than predicted, as well as the deep core region where inverse gradient scale lengths are taken to linearly decrease to zero at $\rho _{{\rm tor}} = 0$![]() .
.
A more practical impact for transport modelling is that it is these power flows, rather than various heating and cooling sources, that constrain what transport processes are active in the plasma. In particular, the ‘fingerprint paradigm’, developed by Kotschenreuther et al. (Reference Kotschenreuther, Liu, Hatch, Mahajan, Zheng, Diallo, Groebner, Hillesheim and Maggi2019) to help identify what transport processes and instabilities act in the pedestal region via ratios of thermal and particle diffusivities can be applied to the plasma core as well. The fact that both plasmas have significant ion thermal transport implies that there must be significant contributions from neoclassical processes and/or ion-scale microturbulence instabilities such as ion temperature gradient (ITG) modes (Horton, Choi & Tang Reference Horton, Choi and Tang1981; Romanelli Reference Romanelli1989) or kinetic ballooning modes (KBMs) (Tang, Connor & Hastie Reference Tang, Connor and Hastie1980) capable of driving experimentally relevant ion thermal fluxes. However, as seen in figure 11, neoclassical ion thermal transport provides negligible contributions to the total thermal transport across most of the core plasma in both cases. In fact, the only time it is predicted to exceed 10 % of the total transport is for $\rho _{{\rm tor}} \le 0.2$![]() in UCR-SS, which we note is in the near-axis region where the gradient scale lengths were assumed to increase linearly with radius, rather than being self-consistently predicted. Such a situation is not unexpected given the low collisionalities inherent to burning plasma conditions, but is notably different from those current day high-performance and steady-state plasmas in which the ion thermal transport is near-neoclassical due to combinations of strong rotational shear and/or Shafranov shift suppression of ion-scale turbulence, larger collisionality and larger poloidal gyroradius than the plasmas considered here.
in UCR-SS, which we note is in the near-axis region where the gradient scale lengths were assumed to increase linearly with radius, rather than being self-consistently predicted. Such a situation is not unexpected given the low collisionalities inherent to burning plasma conditions, but is notably different from those current day high-performance and steady-state plasmas in which the ion thermal transport is near-neoclassical due to combinations of strong rotational shear and/or Shafranov shift suppression of ion-scale turbulence, larger collisionality and larger poloidal gyroradius than the plasmas considered here.

Figure 11. Comparison of total ion power flow fraction $P_i/(P_i + P_e)$![]() (—) with the contribution from NEO (—$\blacksquare$
(—) with the contribution from NEO (—$\blacksquare$![]() —, green) for (a) UCR-P and (b) UCR-SS. Note that although NEO was evaluated at $\rho _{{\rm tor}} = 0.1$
—, green) for (a) UCR-P and (b) UCR-SS. Note that although NEO was evaluated at $\rho _{{\rm tor}} = 0.1$![]() and 0.2 for this plot, these values were not used in the use case development as they lie in the shaded region of $\rho _{{\rm tor}} \le 0.3$
and 0.2 for this plot, these values were not used in the use case development as they lie in the shaded region of $\rho _{{\rm tor}} \le 0.3$![]() where inverse scale lengths are assumed to scale linearly with radius.
where inverse scale lengths are assumed to scale linearly with radius.
Given this essentially negligible neoclassical transport, there must be significant ion-scale instabilities present in both use cases, as illustrated in figure 12. In both plasmas, long wavelength (defined as $k_y \rho _{{\rm sD}} < 1$![]() ) fluctuations propagating in the ion diamagnetic direction are unstable across the entire core region, in addition to short wavelength ($k_y \rho _{{\rm sD}} \ge 1$
) fluctuations propagating in the ion diamagnetic direction are unstable across the entire core region, in addition to short wavelength ($k_y \rho _{{\rm sD}} \ge 1$![]() ) fluctuations propagating in the electron direction. A more accurate analysis of the situation would account for differences in gyroradius between the different ion species, in particular tritium. However, since $\rho _{{\rm sT}} = {\rm sqrt}(M_T/M_D)\rho _{{\rm sD}} \simeq 1.22 \rho _{{\rm sD}}$
) fluctuations propagating in the electron direction. A more accurate analysis of the situation would account for differences in gyroradius between the different ion species, in particular tritium. However, since $\rho _{{\rm sT}} = {\rm sqrt}(M_T/M_D)\rho _{{\rm sD}} \simeq 1.22 \rho _{{\rm sD}}$![]() , this analysis would only introduce minor quantitative changes, and so we retain the above definitions to be consistent with past single hydrogenic species studies. One could also consider treating the deuterium and tritium as a single hydrogenic species with effective mass equal to the average of the two. Such an approach has recently been shown by Belli & Candy (Reference Belli and Candy2021) to accurately reproduce many aspects of the turbulence.
, this analysis would only introduce minor quantitative changes, and so we retain the above definitions to be consistent with past single hydrogenic species studies. One could also consider treating the deuterium and tritium as a single hydrogenic species with effective mass equal to the average of the two. Such an approach has recently been shown by Belli & Candy (Reference Belli and Candy2021) to accurately reproduce many aspects of the turbulence.

Figure 12. Contours of TGLF predictions of the quantity $\mathrm {sgn}(\omega _{{\rm real}}) * \gamma _{{\rm lin}}/(k_y \rho _{{\rm sD}})$![]() for (a) UCR-P and (b) UCR-SS, illustrating the transition in dominant instability propagation in the ion diamagnetic (blue) to electron diamagnetic (red) around $k_y \rho _{{\rm sD}} \sim 1$
for (a) UCR-P and (b) UCR-SS, illustrating the transition in dominant instability propagation in the ion diamagnetic (blue) to electron diamagnetic (red) around $k_y \rho _{{\rm sD}} \sim 1$![]() across the entire simulated region in both cases. The 1/$k_y \rho _{{\rm sD}}$
across the entire simulated region in both cases. The 1/$k_y \rho _{{\rm sD}}$![]() normalization is used to enable comparison of the relative magnitudes of the long- and short-wavelength growth rates in terms of the criterion proposed by Creely et al. (Reference Creely, Rodriguez-Fernandez, Conway, Freethy, Howard and White2019) for significant multiscale contributions. For both cases, that criterion would suggest the long-wavelength modes are strong enough that significant multiscale effects would not be expected.
normalization is used to enable comparison of the relative magnitudes of the long- and short-wavelength growth rates in terms of the criterion proposed by Creely et al. (Reference Creely, Rodriguez-Fernandez, Conway, Freethy, Howard and White2019) for significant multiscale contributions. For both cases, that criterion would suggest the long-wavelength modes are strong enough that significant multiscale effects would not be expected.
Although ion thermal (as well as particle and momentum) transport is most efficiently driven at long wavelengths due to ion gyroaveraging of smaller scales, short wavelength turbulence can drive significant electron thermal transport. These short wavelength contributions to the electron thermal flux $Q_e$![]() are plotted in figure 13. They are minimal (10 % or less of the total transport) in UCR-P, consistent with recent predictions for the inductive SPARC baseline scenario (Howard et al. Reference Howard, Rodriguez-Fernandez, Holland, Rice, Greenwald, Candy and Sciortino2021b). However, even in UCR-SS which has significantly more power flowing through the electrons, the short wavelength modes only contribute 25 % or less of the total thermal flux. Note that these results do not necessarily mean the shorter-wavelength instabilities are a priori negligible, as significant nonlinear cross-scale interactions have been observed in nonlinear multiscale gyrokinetic simulations (Howard et al. Reference Howard, Holland, White, Greenwald and Candy2014; Maeyama et al. Reference Maeyama, Idomura, Watanabe, Nakata, Yagi, Miyato, Ishizawa and Nunami2015; Howard et al. Reference Howard, Holland, White, Greenwald and Candy2016; Holland, Howard & Grierson Reference Holland, Howard and Grierson2017; Maeyama et al. Reference Maeyama, Watanabe, Idomura, Nakata, Ishizawa and Nunami2017; Bonanomi et al. Reference Bonanomi, Mantica, Citrin, Goerler and Teaca2018; Howard et al. Reference Howard, Holland, Rhodes, Candy, Rodriguez-Fernandez, Greenwald, White and Sciortino2021a; Maeyama et al. Reference Maeyama, Watanabe, Nakata, Nunami, Asahi and Ishizawa2022), and a key element of the TGLF SAT1 and SAT2 models is to capture these effects. Therefore, one goal for future studies should be to examine the strength and impact of such couplings at these (or similar) reactor-like parameters.
are plotted in figure 13. They are minimal (10 % or less of the total transport) in UCR-P, consistent with recent predictions for the inductive SPARC baseline scenario (Howard et al. Reference Howard, Rodriguez-Fernandez, Holland, Rice, Greenwald, Candy and Sciortino2021b). However, even in UCR-SS which has significantly more power flowing through the electrons, the short wavelength modes only contribute 25 % or less of the total thermal flux. Note that these results do not necessarily mean the shorter-wavelength instabilities are a priori negligible, as significant nonlinear cross-scale interactions have been observed in nonlinear multiscale gyrokinetic simulations (Howard et al. Reference Howard, Holland, White, Greenwald and Candy2014; Maeyama et al. Reference Maeyama, Idomura, Watanabe, Nakata, Yagi, Miyato, Ishizawa and Nunami2015; Howard et al. Reference Howard, Holland, White, Greenwald and Candy2016; Holland, Howard & Grierson Reference Holland, Howard and Grierson2017; Maeyama et al. Reference Maeyama, Watanabe, Idomura, Nakata, Ishizawa and Nunami2017; Bonanomi et al. Reference Bonanomi, Mantica, Citrin, Goerler and Teaca2018; Howard et al. Reference Howard, Holland, Rhodes, Candy, Rodriguez-Fernandez, Greenwald, White and Sciortino2021a; Maeyama et al. Reference Maeyama, Watanabe, Nakata, Nunami, Asahi and Ishizawa2022), and a key element of the TGLF SAT1 and SAT2 models is to capture these effects. Therefore, one goal for future studies should be to examine the strength and impact of such couplings at these (or similar) reactor-like parameters.

Figure 13. Comparison of total ion power flow fraction $P_i/(P_i + P_e)$![]() (—) to the contribution from high-$k$
(—) to the contribution from high-$k$![]() $(k_y \rho _{{\rm sD}} > 1)$
$(k_y \rho _{{\rm sD}} > 1)$![]() fluctuations (—$\blacksquare$
fluctuations (—$\blacksquare$![]() —, purple) for (a) UCR-P and (b) UCR-SS.
—, purple) for (a) UCR-P and (b) UCR-SS.
3.2. Impact of TGLF model choices
Having established that long-wavelength microturbulence is the dominant transport-driving process in these scenarios, we next focus on characterizing some key elements of this turbulence. As indicated by figure 12, the turbulence at these scales propagates in the ion diamagnetic direction, consistent with the primary driving instabilities being a mix of ITG and KBM modes. These instabilities are also consistent with the fingerprint requirement needed to drive significant ion thermal transport, but are expected to have significantly different impacts on particle transport. Namely, it is well known that ITG modes can have an associated particle pinch as well as diffusivity, enabling peaked density profiles even in the absence of a particle source (Angioni et al. Reference Angioni, Fable, Greenwald, Maslov, Peeters, Takenaga and Weisen2009). However, as an effectively MHD-like mode driven by total pressure, the KBM is generally assumed to drive only a particle outflow, with little to no pinch (Kotschenreuther et al. Reference Kotschenreuther, Liu, Hatch, Mahajan, Zheng, Diallo, Groebner, Hillesheim and Maggi2019). However, KBM-driven particle transport has not been studied in detail, particularly for the low collisionality core plasma conditions under discussion here, and so it represents another potential avenue for future research.
In addition to ITG and KBM modes, trapped electron modes (TEMs) are also present, both as the dominant mode near the $k_y \rho _{{\rm sD}} \sim 1$![]() ‘dividing line’ and as an unstable but subdominant mode at longer wavelengths. Although TEMs are generally associated with particle and electron thermal transport, they can also drive non-negligible ion thermal transport (albeit generally less than ITG modes for comparable parameters). Past studies of burning and non-burning plasmas (Fable, Angioni & Sauter Reference Fable, Angioni and Sauter2009; Grierson et al. Reference Grierson, Staebler, Solomon, McKee, Holland, Austin, Marinoni, Schmitz and Pinsker2018; Fable et al. Reference Fable, Angioni, Bobkov, Stober, Bilato, Conway, Goerler, McDermott, Puetterich and Siccinio2019; Mantica et al. Reference Mantica, Angioni, Bonanomi, Citrin, Grierson, Koechl, Mariani and Staebler2020; Howard et al. Reference Howard, Rodriguez-Fernandez, Holland, Rice, Greenwald, Candy and Sciortino2021b; Li et al. Reference Li, Li, Fu, Wang and Jiang2022; Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard and Candy2022b) have found that the total particle flux can be a sensitive function of the mix of ITG and TEM turbulence present, and gyrokinetic simulations have shown that nonlinear couplings between these modes are possible (Merz & Jenko Reference Merz and Jenko2010). Finally, in principle, long binormal (but short radial) wavelength microtearing modes may also be unstable, but these modes are not accurately captured by TGLF due to their non-ballooning mode structure and so are inherently unable to impact the predicted profiles in workflow used here. While this omission should of course be investigated via future gyrokinetic analyses, past gyrokinetic simulations of conditions where both MTM and ITG modes are robustly unstable have generally found the ITG modes to dominate and the MTM instability to drive negligible contributions (Jian et al. Reference Jian, Holland, Ding, Knolker, Snyder, Chan, Garofalo and Grierson2022a).
‘dividing line’ and as an unstable but subdominant mode at longer wavelengths. Although TEMs are generally associated with particle and electron thermal transport, they can also drive non-negligible ion thermal transport (albeit generally less than ITG modes for comparable parameters). Past studies of burning and non-burning plasmas (Fable, Angioni & Sauter Reference Fable, Angioni and Sauter2009; Grierson et al. Reference Grierson, Staebler, Solomon, McKee, Holland, Austin, Marinoni, Schmitz and Pinsker2018; Fable et al. Reference Fable, Angioni, Bobkov, Stober, Bilato, Conway, Goerler, McDermott, Puetterich and Siccinio2019; Mantica et al. Reference Mantica, Angioni, Bonanomi, Citrin, Grierson, Koechl, Mariani and Staebler2020; Howard et al. Reference Howard, Rodriguez-Fernandez, Holland, Rice, Greenwald, Candy and Sciortino2021b; Li et al. Reference Li, Li, Fu, Wang and Jiang2022; Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard and Candy2022b) have found that the total particle flux can be a sensitive function of the mix of ITG and TEM turbulence present, and gyrokinetic simulations have shown that nonlinear couplings between these modes are possible (Merz & Jenko Reference Merz and Jenko2010). Finally, in principle, long binormal (but short radial) wavelength microtearing modes may also be unstable, but these modes are not accurately captured by TGLF due to their non-ballooning mode structure and so are inherently unable to impact the predicted profiles in workflow used here. While this omission should of course be investigated via future gyrokinetic analyses, past gyrokinetic simulations of conditions where both MTM and ITG modes are robustly unstable have generally found the ITG modes to dominate and the MTM instability to drive negligible contributions (Jian et al. Reference Jian, Holland, Ding, Knolker, Snyder, Chan, Garofalo and Grierson2022a).
Given the mix of instabilities present, and the tightly-coupled interplay in a burning plasma among transport, temperature profiles, density profiles and self-heating, it is not surprising that predictions of scenario performance depend sensitively on the physics assumptions and model of turbulence saturation used. One example of this sensitivity is shown in figure 14, which contrasts the predictions for UCR-P and UCR-SS presented above with the results of assuming the turbulence is electrostatic and setting perpendicular magnetic fluctuation amplitudes to zero. To enable a cleaner comparison, the safety factor profile is held fixed in both cases. This choice completely eliminates the inherently electromagnetic KBM from the predicted turbulence mix, as well as the stabilization of predominantly electrostatic ITG modes via their coupling to Alfvèn waves (Terry et al. Reference Terry, Carmody, Doerk, Guttenfelder, Hatch, Hegna, Ishizawa, Jenko, Nevins and Predebon2015). As can be seen in figure 14(a,b), the ion and electron temperatures are predicted to be slightly lower in UCR-P and substantially so in UCR-SS, reflecting the significant electromagnetic stabilization of the ITG turbulence in UCR-SS. However, these decreases in temperature are accompanied by increases in the predicted density peaking for both cases. For UCR-P, the net impact is minimal, with the predicted $Q_{{\rm fusion}}$![]() increasing slightly from 27.3 in the electromagnetic case to 28.3 in the electrostatic case. However, there is a nearly 30 % drop in $Q_{{\rm fusion}}$
increasing slightly from 27.3 in the electromagnetic case to 28.3 in the electrostatic case. However, there is a nearly 30 % drop in $Q_{{\rm fusion}}$![]() (12.9–8.8) for the UCR-SS scenario, although it must be emphasized the electrostatic profile predictions would correspond to a significantly different bootstrap current not consistent with the assumption of fixed safety factor used in the calculations.
(12.9–8.8) for the UCR-SS scenario, although it must be emphasized the electrostatic profile predictions would correspond to a significantly different bootstrap current not consistent with the assumption of fixed safety factor used in the calculations.

Figure 14. Comparison of predicted (a) ion temperature $T_i$![]() , (b) electron temperature $T_e$
, (b) electron temperature $T_e$![]() and (c) electron density $n_e$
and (c) electron density $n_e$![]() with $\delta B_{\perp }$
with $\delta B_{\perp }$![]() fluctuations included for UCR-P (—, blue) and UCR-SS (—, red) versus with only electrostatic fluctuations ($\delta B_{\perp } = 0$
fluctuations included for UCR-P (—, blue) and UCR-SS (—, red) versus with only electrostatic fluctuations ($\delta B_{\perp } = 0$![]() ) (— —). The safety factor $q$
) (— —). The safety factor $q$![]() is held fixed in these simulations.
is held fixed in these simulations.
The choice of turbulence saturation rule used can have an even larger impact on predictions of plasma performance. Figure 15 compares predictions of UCR-P temperature and density profiles using the TGLF SAT0 (Staebler et al. Reference Staebler, Kinsey and Waltz2007), SAT1 (Staebler et al. Reference Staebler, Candy, Howard and Holland2016) and SAT2 (Staebler et al. Reference Staebler, Belli, Candy, Kinsey, Dudding and Patel2021) saturation rules, with all other settings and assumptions (including finite magnetic fluctuations), as well as safety factor profile, held fixed. Relative to the SAT1 model used in most of this paper, the use of SAT0 leads to not only higher temperatures, but also broad peaking of the density profile, such that $Q_{{\rm fusion}}$![]() increases from 27 (for SAT1) to 51 (for SAT0). The use of SAT2 leads to lower temperature profiles across the simulated domain, but also generates stronger density peaking (although it is more localized than the SAT0 predictions), with a net effect of lowering $Q_{{\rm fusion}}$
increases from 27 (for SAT1) to 51 (for SAT0). The use of SAT2 leads to lower temperature profiles across the simulated domain, but also generates stronger density peaking (although it is more localized than the SAT0 predictions), with a net effect of lowering $Q_{{\rm fusion}}$![]() relative to the SAT1 prediction of 27–21. Even more dramatic impacts are found for the UCR-SS scenario, such that meaningful converged results cannot be achieved while keeping parameters such as toroidal field strength, plasma shape and pedestal pressure fixed. In the case of SAT0, the combination of lower transport and strong $\beta$
relative to the SAT1 prediction of 27–21. Even more dramatic impacts are found for the UCR-SS scenario, such that meaningful converged results cannot be achieved while keeping parameters such as toroidal field strength, plasma shape and pedestal pressure fixed. In the case of SAT0, the combination of lower transport and strong $\beta$![]() stabilization essentially leads to an ignited plasma whose pressure runs away past all global stability limits, while using SAT2 leads to a radiative collapse of the plasma, with negligible fusion power generated.
stabilization essentially leads to an ignited plasma whose pressure runs away past all global stability limits, while using SAT2 leads to a radiative collapse of the plasma, with negligible fusion power generated.

Figure 15. Comparison of predicted (a) ion temperature $T_i$![]() , (b) electron temperature $T_e$
, (b) electron temperature $T_e$![]() and (c) electron density $n_e$
and (c) electron density $n_e$![]() for UCR-P using the SAT0 (— - —, cyan), SAT1 (—, blue), and SAT2 (— —) saturation rules. The safety factor $q$
for UCR-P using the SAT0 (— - —, cyan), SAT1 (—, blue), and SAT2 (— —) saturation rules. The safety factor $q$![]() is held fixed in these simulations and all include perpendicular magnetic fluctuations.
is held fixed in these simulations and all include perpendicular magnetic fluctuations.
Understanding the physics that drives the differences in saturation rule predictions is clearly vital for accurate design and optimization of future reactors. On one hand, it should be noted that SAT2 matches the calibration database of nonlinear CGYRO simulations much better than SAT1 does, and that both do much better than SAT0. However, at the same time, that database is predominantly centred around the ‘GA-STD’ case parameters (Waltz, Kerbel & Milovich Reference Waltz, Kerbel and Milovich1994), which are more representative of an essentially electrostatic, more collisional L-mode plasma than the UCR plasmas examined here. Furthermore, while transport predictions with SAT2 have exhibited improved agreement for L-mode plasmas (Angioni et al. Reference Angioni, Gamot, Tardini, Fable, Luda, Bonanomi, Kiefer and Staebler2022), it is less clear that its performance is significantly better in H-mode discharges (Mantica et al. Reference Mantica, Bonanomi, Mariani, Carvalho, Delabie, Garcia, Hawkes, Johnson, Keeling and Sertoli2021; Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard and Candy2022b). Therefore, it is vital to improve our understanding of the transport physics at these parameters to develop more efficient predictive models suitable for efficient reactor design and optimization.
3.3. Comparison of TGLF stiffness predictions
The results presented in the previous section show how different models of turbulent transport can impact the overall performance of the predicted scenario. Additional insight into these effects can be obtained by examining the local stiffness of the predicted turbulence at different radii in the plasma. Although various definitions and measures of global and local transport stiffness as observed in experiments, theory and simulation have been proposed in the literature (see e.g. Garbet et al. Reference Garbet, Mantica, Ryter, Cordey, Imbeaux, Sozzi, Manini, Asp, Parail and Wolf2004; Waltz, Candy & Petty Reference Waltz, Candy and Petty2006; Mantica et al. Reference Mantica, Strintzi, Tala, Giroud, Johnson, Leggate, Lerche, Loarer, Peeters and Salmi2009; Luce et al. Reference Luce, Burrell, Holland, Marinoni, Petty, Smith, Austin, Grierson and Zeng2018; Holland et al. Reference Holland, Luce, Grierson, Smith, Marinoni, Burrell, Petty and Bass2021), here we only examine how the predicted fluxes scale with driving gradients while holding all other parameters fixed. It therefore differs from what can be achieved experimentally (or in self-consistent, flux-matched simulations), where varying the gradients at one location inherently changes plasma parameters (and thus the transport) at other radii, but does enable direct connection with underlying theoretical models of local turbulent transport.
Complementing figure 14 above, figures 16 and 17 show how the SAT1 predictions for ion ($Q_i$![]() ) and electron ($Q_e$
) and electron ($Q_e$![]() ) energy fluxes, as well as the electron particle flux $\varGamma _e$
) energy fluxes, as well as the electron particle flux $\varGamma _e$![]() , scale with the local ion temperature gradient. The particle flux is normalized to the gyroBohm flux $\varGamma _{gB} = n_e c_{{\rm sD}}(\rho _{{\rm sD}}/a)^2$
, scale with the local ion temperature gradient. The particle flux is normalized to the gyroBohm flux $\varGamma _{gB} = n_e c_{{\rm sD}}(\rho _{{\rm sD}}/a)^2$![]() and the energy flux to $Q_{gB} = n_e T_e c_{{\rm sD}}(\rho _{{\rm sD}}/a)^2$
and the energy flux to $Q_{gB} = n_e T_e c_{{\rm sD}}(\rho _{{\rm sD}}/a)^2$![]() , where $\rho _{{\rm sD}}$
, where $\rho _{{\rm sD}}$![]() is calculated using $B_{unit}$
is calculated using $B_{unit}$![]() as defined by Candy et al. (Reference Candy, Belli and Bravenec2016). In these scans, all other parameters, both dimensional (e.g. $n_e$
as defined by Candy et al. (Reference Candy, Belli and Bravenec2016). In these scans, all other parameters, both dimensional (e.g. $n_e$![]() , $T_e$
, $T_e$![]() and $T_i$
and $T_i$![]() ) and dimensionless (e.g. $\beta$
) and dimensionless (e.g. $\beta$![]() , $T_i/T_e$
, $T_i/T_e$![]() and $R/L_{{\rm Ti}}$
and $R/L_{{\rm Ti}}$![]() ), are held fixed including the pressure gradient contribution to the magnetic drift frequency. Thus, variations in $R/L_{{\rm Ti}}$
), are held fixed including the pressure gradient contribution to the magnetic drift frequency. Thus, variations in $R/L_{{\rm Ti}}$![]() are equivalent to variations in $dT_i/dr$
are equivalent to variations in $dT_i/dr$![]() . The results are plotted as a function of $R/L_{{\rm Ti}}$
. The results are plotted as a function of $R/L_{{\rm Ti}}$![]() , which was varied from zero to twice the predicted value at each of the four radii considered. The electron temperature gradient $R/L_{Te}$
, which was varied from zero to twice the predicted value at each of the four radii considered. The electron temperature gradient $R/L_{Te}$![]() was also rescaled by the same proportion as $R/L_{{\rm Ti}}$
was also rescaled by the same proportion as $R/L_{{\rm Ti}}$![]() , but is not plotted to simplify the presentation of results.
, but is not plotted to simplify the presentation of results.

Figure 16. Comparison of TGLF SAT1 electromagnetic gyroBohm-normalized (a–d) ion and electron energy fluxes $Q_i/Q_{gB}$![]() ($\blacktriangle$
($\blacktriangle$![]() , green) and $Q_e/Q_{gB}$
, green) and $Q_e/Q_{gB}$![]() ($\blacktriangleleft$
($\blacktriangleleft$![]() , purple) to the corresponding electrostatic predictions ($\blacktriangledown$
, purple) to the corresponding electrostatic predictions ($\blacktriangledown$![]() , lime; $\blacktriangleright$
, lime; $\blacktriangleright$![]() , magenta) in UCR-P at $\rho _{{\rm tor}} = 0.3, 0.5, 0.7\ \mathrm {and} \ 0.9$
, magenta) in UCR-P at $\rho _{{\rm tor}} = 0.3, 0.5, 0.7\ \mathrm {and} \ 0.9$![]() in panels (a–d), respectively, as a function of $R/L_{{\rm Ti}}$
in panels (a–d), respectively, as a function of $R/L_{{\rm Ti}}$![]() . The corresponding electromagnetic ($\blacksquare$
. The corresponding electromagnetic ($\blacksquare$![]() , grey) and electrostatic ($\blacklozenge$
, grey) and electrostatic ($\blacklozenge$![]() , light grey) normalized particle flux predictions are shown in panels (e–h). Note that $R/L_{Te}$
, light grey) normalized particle flux predictions are shown in panels (e–h). Note that $R/L_{Te}$![]() is scaled by the same factor as $R/L_{{\rm Ti}}$
is scaled by the same factor as $R/L_{{\rm Ti}}$![]() is relative to the baseline prediction, but is not plotted to simplify the presentation.
is relative to the baseline prediction, but is not plotted to simplify the presentation.

Figure 17. Comparison of TGLF SAT1 electromagnetic gyroBohm-normalized (a–d) ion and electron energy fluxes $Q_i/Q_{gB}$![]() ($\blacktriangle$
($\blacktriangle$![]() , green) and $Q_e/Q_{gB}$
, green) and $Q_e/Q_{gB}$![]() ($\blacktriangleleft$
($\blacktriangleleft$![]() , purple) to the corresponding electrostatic predictions ($\blacktriangledown$
, purple) to the corresponding electrostatic predictions ($\blacktriangledown$![]() , lime; $\blacktriangleright$
, lime; $\blacktriangleright$![]() , magenta) in UCR-SS at $\rho _{{\rm tor}} = 0.3, 0.5, 0.7 \ \mathrm {and} \ 0.9$
, magenta) in UCR-SS at $\rho _{{\rm tor}} = 0.3, 0.5, 0.7 \ \mathrm {and} \ 0.9$![]() in panels (a–d), respectively, as a function of $R/L_{{\rm Ti}}$
in panels (a–d), respectively, as a function of $R/L_{{\rm Ti}}$![]() . The corresponding electromagnetic ($\blacksquare$
. The corresponding electromagnetic ($\blacksquare$![]() , grey) and electrostatic ($\blacklozenge$
, grey) and electrostatic ($\blacklozenge$![]() , light grey) normalized particle flux predictions are shown in panels (e–h). Note that $R/L_{Te}$
, light grey) normalized particle flux predictions are shown in panels (e–h). Note that $R/L_{Te}$![]() is scaled by the same factor as $R/L_{{\rm Ti}}$
is scaled by the same factor as $R/L_{{\rm Ti}}$![]() is relative to the baseline prediction, but is not plotted to simplify the presentation.
is relative to the baseline prediction, but is not plotted to simplify the presentation.
Examination of figure 16(a–d) shows that the predicted energy transport in UCR-P is almost completely electrostatic at all four radii considered, consistent with its relatively moderate value of $\beta$![]() and previous examinations of predicted transport for other inductive burning plasma scenarios (Grierson et al. Reference Grierson, Staebler, Solomon, McKee, Holland, Austin, Marinoni, Schmitz and Pinsker2018; Mantica et al. Reference Mantica, Angioni, Bonanomi, Citrin, Grierson, Koechl, Mariani and Staebler2020; Howard et al. Reference Howard, Rodriguez-Fernandez, Holland, Rice, Greenwald, Candy and Sciortino2021b). However, the corresponding particle transport predictions shown in figure 16(e–h) show a dramatic impact from including magnetic fluctuations, with the reversal of the particle flux sign as well as changes in scaling of the magnitude with gradients at all radii except $\rho _{{\rm tor}} = 0.7$
and previous examinations of predicted transport for other inductive burning plasma scenarios (Grierson et al. Reference Grierson, Staebler, Solomon, McKee, Holland, Austin, Marinoni, Schmitz and Pinsker2018; Mantica et al. Reference Mantica, Angioni, Bonanomi, Citrin, Grierson, Koechl, Mariani and Staebler2020; Howard et al. Reference Howard, Rodriguez-Fernandez, Holland, Rice, Greenwald, Candy and Sciortino2021b). However, the corresponding particle transport predictions shown in figure 16(e–h) show a dramatic impact from including magnetic fluctuations, with the reversal of the particle flux sign as well as changes in scaling of the magnitude with gradients at all radii except $\rho _{{\rm tor}} = 0.7$![]() . In particular, the increased core density peaking observed in the electrostatic UCR-P simulation shown in figure 14 can be straightforwardly understood in terms of figure 16(e–f), which predicts that increased particle outflow (i.e. flattening) at those radii should result in electromagnetic stabilization as the temperature gradients increase, whereas the electrostatic simulations predict increased inflow (peaking) as the temperature gradients increase. Thus, in the electrostatic simulation, a small amount of increased density peaking (due to small differences at nominal parameters) leads to increased fusion production, which in turn provides additional heating to increase the temperature gradients. However, as the density increases, radiative losses and the gyroBohm normalization $Q_{gB}$
. In particular, the increased core density peaking observed in the electrostatic UCR-P simulation shown in figure 14 can be straightforwardly understood in terms of figure 16(e–f), which predicts that increased particle outflow (i.e. flattening) at those radii should result in electromagnetic stabilization as the temperature gradients increase, whereas the electrostatic simulations predict increased inflow (peaking) as the temperature gradients increase. Thus, in the electrostatic simulation, a small amount of increased density peaking (due to small differences at nominal parameters) leads to increased fusion production, which in turn provides additional heating to increase the temperature gradients. However, as the density increases, radiative losses and the gyroBohm normalization $Q_{gB}$![]() also increase, such that the final state is actually one with higher density and lower temperatures. The impact of finite magnetic fluctuations has been studied (Angioni et al. Reference Angioni, Fable, Greenwald, Maslov, Peeters, Takenaga and Weisen2009) and observed (Fable et al. Reference Fable, Angioni, Bobkov, Stober, Bilato, Conway, Goerler, McDermott, Puetterich and Siccinio2019) in some previous burning plasma scenario modelling. The basic physical mechanism underlying their impact is believed to be a breaking of passing electron adiabaticity or even stochastization by the magnetic fluctuations (Nevins, Wang & Candy Reference Nevins, Wang and Candy2011), enabling outward transport to overcome the well-known electrostatic pinch mechanisms driven by e.g. the magnetic curvature drift. However, more study on this topic is needed, as recent gyrokinetic profile predictions for SPARC by Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard and Candy2022b) found significantly stronger density peaking than predicted by TGLF.
also increase, such that the final state is actually one with higher density and lower temperatures. The impact of finite magnetic fluctuations has been studied (Angioni et al. Reference Angioni, Fable, Greenwald, Maslov, Peeters, Takenaga and Weisen2009) and observed (Fable et al. Reference Fable, Angioni, Bobkov, Stober, Bilato, Conway, Goerler, McDermott, Puetterich and Siccinio2019) in some previous burning plasma scenario modelling. The basic physical mechanism underlying their impact is believed to be a breaking of passing electron adiabaticity or even stochastization by the magnetic fluctuations (Nevins, Wang & Candy Reference Nevins, Wang and Candy2011), enabling outward transport to overcome the well-known electrostatic pinch mechanisms driven by e.g. the magnetic curvature drift. However, more study on this topic is needed, as recent gyrokinetic profile predictions for SPARC by Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard and Candy2022b) found significantly stronger density peaking than predicted by TGLF.
Qualitatively similar trends in the particle fluxes are found for the corresponding UCR-SS scans shown in figure 17, but there are clearer and more significant differences between the electrostatic and electromagnetic energy flux predictions, in keeping with its larger $\beta$![]() . Consistent with some previous studies (for example, Citrin et al. Reference Citrin, Garcia, Gorler, Jenko, Mantica, Told, Bourdelle, Hatch, Hogeweij and Johnson2014; Mantica et al. Reference Mantica, Angioni, Bonanomi, Citrin, Grierson, Koechl, Mariani and Staebler2020; Holland et al. Reference Holland, Luce, Grierson, Smith, Marinoni, Burrell, Petty and Bass2021), the primary qualitative impact of including magnetic fluctuations is to change the stiffness of the predicted transport, rather than impact the effective critical gradient below which there is little to no transport driven. At lower values of $R/L_{{\rm Ti}}$
. Consistent with some previous studies (for example, Citrin et al. Reference Citrin, Garcia, Gorler, Jenko, Mantica, Told, Bourdelle, Hatch, Hogeweij and Johnson2014; Mantica et al. Reference Mantica, Angioni, Bonanomi, Citrin, Grierson, Koechl, Mariani and Staebler2020; Holland et al. Reference Holland, Luce, Grierson, Smith, Marinoni, Burrell, Petty and Bass2021), the primary qualitative impact of including magnetic fluctuations is to change the stiffness of the predicted transport, rather than impact the effective critical gradient below which there is little to no transport driven. At lower values of $R/L_{{\rm Ti}}$![]() , the electromagnetic $Q_i$
, the electromagnetic $Q_i$![]() and $Q_e$
and $Q_e$![]() values are either lower than ($\rho _{{\rm tor}} = 0.3$
values are either lower than ($\rho _{{\rm tor}} = 0.3$![]() and 0.7) or equal to ($\rho _{{\rm tor}} = 0.5$
and 0.7) or equal to ($\rho _{{\rm tor}} = 0.5$![]() and 0.9) the electrostatic predictions, consistent with stabilization of ITG turbulence via coupling to Alfvèn waves and/or changes to the magnetic drift due to increased $\alpha$
and 0.9) the electrostatic predictions, consistent with stabilization of ITG turbulence via coupling to Alfvèn waves and/or changes to the magnetic drift due to increased $\alpha$![]() (proportional to $-(q^2R/B^2)\,{\rm d}p/{\rm d}r$
(proportional to $-(q^2R/B^2)\,{\rm d}p/{\rm d}r$![]() in circular geometry).
in circular geometry).
However, at $\rho _{{\rm tor}} = 0.7$![]() , for values of $R/L_{{\rm Ti}} \le 15$
, for values of $R/L_{{\rm Ti}} \le 15$![]() , the electromagnetic $Q_e$
, the electromagnetic $Q_e$![]() prediction is actually larger than $Q_i$
prediction is actually larger than $Q_i$![]() or the electrostatic predictions for which $Q_e \simeq Q_i$
or the electrostatic predictions for which $Q_e \simeq Q_i$![]() . There are several processes that drive this result. First, the electromagnetic stabilization of the long-wavelength ITG turbulence enables an increased amount of shorter-wavelength turbulence to drive significant $Q_e$
. There are several processes that drive this result. First, the electromagnetic stabilization of the long-wavelength ITG turbulence enables an increased amount of shorter-wavelength turbulence to drive significant $Q_e$![]() but not $Q_i$
but not $Q_i$![]() . However, as $R/L_{{\rm Ti}}$
. However, as $R/L_{{\rm Ti}}$![]() increases, the long-wavelength turbulence becomes strong enough to suppress the shorter wavelength fluctuations and one obtains a situation where $Q_e$
increases, the long-wavelength turbulence becomes strong enough to suppress the shorter wavelength fluctuations and one obtains a situation where $Q_e$![]() and $Q_i$
and $Q_i$![]() scale similarly with increased drive. These cross-scale interactions have been observed in nonlinear multiscale gyrokinetic simulations (Howard et al. Reference Howard, Holland, White, Greenwald and Candy2014; Maeyama et al. Reference Maeyama, Idomura, Watanabe, Nakata, Yagi, Miyato, Ishizawa and Nunami2015; Howard et al. Reference Howard, Holland, White, Greenwald and Candy2016; Holland et al. Reference Holland, Howard and Grierson2017; Maeyama et al. Reference Maeyama, Watanabe, Idomura, Nakata, Ishizawa and Nunami2017; Bonanomi et al. Reference Bonanomi, Mantica, Citrin, Goerler and Teaca2018; Howard et al. Reference Howard, Holland, Rhodes, Candy, Rodriguez-Fernandez, Greenwald, White and Sciortino2021a; Maeyama et al. Reference Maeyama, Watanabe, Nakata, Nunami, Asahi and Ishizawa2022), and capturing their physics is a key advance of the SAT1 (and SAT2) saturation rules over the SAT0 model. Given that such simulations have only been done for a relatively limited number of parameters, mostly corresponding to current-day tokamak plasmas, this question should be studied further at these reactor-relevant parameters. Indeed, some recent studies (Mariani et al. Reference Mariani, Mantica, Casiraghi, Citrin, Görler and Staebler2021; Citrin et al. Reference Citrin, Maeyama, Angioni, Bonanomi, Bourdelle, Casson, Fable, Görler, Mantica and Mariani2022) have identified cases where multiscale effects are not found to be significant even when ‘rule-of-thumb’ criteria (as proposed in e.g. Howard et al. Reference Howard, Holland, White, Greenwald and Candy2016; Creely et al. Reference Creely, Rodriguez-Fernandez, Conway, Freethy, Howard and White2019) suggest they should. Moreover, the electromagnetic TGLF calculations also show significant contributions to electron transport from intermediate-scale ($k_y \rho _{{\rm sD}} \sim 2 \unicode{x2013} 4$
scale similarly with increased drive. These cross-scale interactions have been observed in nonlinear multiscale gyrokinetic simulations (Howard et al. Reference Howard, Holland, White, Greenwald and Candy2014; Maeyama et al. Reference Maeyama, Idomura, Watanabe, Nakata, Yagi, Miyato, Ishizawa and Nunami2015; Howard et al. Reference Howard, Holland, White, Greenwald and Candy2016; Holland et al. Reference Holland, Howard and Grierson2017; Maeyama et al. Reference Maeyama, Watanabe, Idomura, Nakata, Ishizawa and Nunami2017; Bonanomi et al. Reference Bonanomi, Mantica, Citrin, Goerler and Teaca2018; Howard et al. Reference Howard, Holland, Rhodes, Candy, Rodriguez-Fernandez, Greenwald, White and Sciortino2021a; Maeyama et al. Reference Maeyama, Watanabe, Nakata, Nunami, Asahi and Ishizawa2022), and capturing their physics is a key advance of the SAT1 (and SAT2) saturation rules over the SAT0 model. Given that such simulations have only been done for a relatively limited number of parameters, mostly corresponding to current-day tokamak plasmas, this question should be studied further at these reactor-relevant parameters. Indeed, some recent studies (Mariani et al. Reference Mariani, Mantica, Casiraghi, Citrin, Görler and Staebler2021; Citrin et al. Reference Citrin, Maeyama, Angioni, Bonanomi, Bourdelle, Casson, Fable, Görler, Mantica and Mariani2022) have identified cases where multiscale effects are not found to be significant even when ‘rule-of-thumb’ criteria (as proposed in e.g. Howard et al. Reference Howard, Holland, White, Greenwald and Candy2016; Creely et al. Reference Creely, Rodriguez-Fernandez, Conway, Freethy, Howard and White2019) suggest they should. Moreover, the electromagnetic TGLF calculations also show significant contributions to electron transport from intermediate-scale ($k_y \rho _{{\rm sD}} \sim 2 \unicode{x2013} 4$![]() ) magnetic fluctuations, as well as destabilization of long-wavelength KBMs at higher gradients. Understanding the impact of these electromagnetic effects on cross-scale turbulent interactions has received limited study to date (Maeyama et al. Reference Maeyama, Idomura, Watanabe, Nakata, Yagi, Miyato, Ishizawa and Nunami2015, Reference Maeyama, Watanabe, Idomura, Nakata, Ishizawa and Nunami2017), but may be vital for accurate transport predictions in advanced tokamak scenarios. The extreme differences in stiffness observed at $\rho _{{\rm tor}} = 0.5$
) magnetic fluctuations, as well as destabilization of long-wavelength KBMs at higher gradients. Understanding the impact of these electromagnetic effects on cross-scale turbulent interactions has received limited study to date (Maeyama et al. Reference Maeyama, Idomura, Watanabe, Nakata, Yagi, Miyato, Ishizawa and Nunami2015, Reference Maeyama, Watanabe, Idomura, Nakata, Ishizawa and Nunami2017), but may be vital for accurate transport predictions in advanced tokamak scenarios. The extreme differences in stiffness observed at $\rho _{{\rm tor}} = 0.5$![]() and 0.9 also appear to be due to the onset of KBMs at the longest wavelength ($k_y \rho _{{\rm sD}} = 0.1$
and 0.9 also appear to be due to the onset of KBMs at the longest wavelength ($k_y \rho _{{\rm sD}} = 0.1$![]() ) used in the TGLF calculations.
) used in the TGLF calculations.
The different physics embodied in each of the saturation rules also leads to quite different predictions of performance, as figure 15 and its discussion above illustrate. The practical manifestation of these differences can be seen in the local stiffness calculations shown in figure 18. For simplicity, only the total energy flux $Q_{{\rm tot}} = Q_i + Q_e$![]() is plotted and the calculations include electromagnetic fluctuations. The large X symbols indicate the predicted power balance fluxes and gradients at each radius. At almost every location in both scenarios, all three models predict a similar critical gradient. In comparing these predictions, it should be recalled that SAT0 and SAT1 share the same linear physics model, but use different scalings of fluctuation intensity, whereas SAT2 incorporates changes to the collision model and geometric factors as well as changes to the saturation rule scaling. However, these are low collisionality plasmas and the geometric factors primarily impact growth rate and flux scalings above the threshold instead of the threshold itself, and so such consistency in the critical gradient is not unexpected. More prominent are the differences in stiffness (the slope of the flux versus $R/L_{{\rm Ti}}$
is plotted and the calculations include electromagnetic fluctuations. The large X symbols indicate the predicted power balance fluxes and gradients at each radius. At almost every location in both scenarios, all three models predict a similar critical gradient. In comparing these predictions, it should be recalled that SAT0 and SAT1 share the same linear physics model, but use different scalings of fluctuation intensity, whereas SAT2 incorporates changes to the collision model and geometric factors as well as changes to the saturation rule scaling. However, these are low collisionality plasmas and the geometric factors primarily impact growth rate and flux scalings above the threshold instead of the threshold itself, and so such consistency in the critical gradient is not unexpected. More prominent are the differences in stiffness (the slope of the flux versus $R/L_{{\rm Ti}}$![]() ) between the models at many of the locations examined. In a few cases, such as $\rho _{{\rm tor}} = 0.3$
) between the models at many of the locations examined. In a few cases, such as $\rho _{{\rm tor}} = 0.3$![]() and 0.5 in the UCR-P scenario, all three models predict relatively similar stiffness, with SAT0 and SAT1 particularly close. However, at most radii, one finds SAT1 to predict stiffer transport than SAT0, and SAT2 stiffer transport than SAT1.
and 0.5 in the UCR-P scenario, all three models predict relatively similar stiffness, with SAT0 and SAT1 particularly close. However, at most radii, one finds SAT1 to predict stiffer transport than SAT0, and SAT2 stiffer transport than SAT1.

Figure 18. Comparisons of different TGLF saturation rule predictions of the electromagnetic normalized total energy flux $Q_{{\rm tot}}/Q_gB = (Q_i + Q_e)/Q_{gB}$![]() for (a–d) UCR-P and (e–h) UCR-SS at $\rho _{{\rm tor}} = 0.3, 0.5, 0.7 \ \mathrm {and}\ 0.9$
for (a–d) UCR-P and (e–h) UCR-SS at $\rho _{{\rm tor}} = 0.3, 0.5, 0.7 \ \mathrm {and}\ 0.9$![]() . Note that $R/L_{Te}$
. Note that $R/L_{Te}$![]() is scaled by the same factor as $R/L_{{\rm Ti}}$
is scaled by the same factor as $R/L_{{\rm Ti}}$![]() is relative to the baseline prediction, but is not plotted to simplify the presentation. The large Xs indicate the nominal gradients and fluxes for each location.
is relative to the baseline prediction, but is not plotted to simplify the presentation. The large Xs indicate the nominal gradients and fluxes for each location.
Another key feature of these results is that in both scenarios at $\rho _{{\rm tor}} = 0.9$![]() (figure 16d,h), the calculations indicate a rapid change in stiffness, suggesting a change in the dominant instability (likely from ITG to KBM), but the gradient(s) at which this transition occurs depend strongly on the saturation rule. Like the differences in stiffness, SAT0 predicts the highest threshold for the switch to extremely stiff transport, and SAT2 the lowest. Given that SAT2 predicts the stiffest transport and lowest critical gradients, it is not surprising that it yields the lowest performance, or that SAT0 provides more optimistic predictions than SAT1 given its lower stiffness and equal or higher critical gradients. These differences are further magnified because any change at $\rho _{{\rm tor}} = 0.9$
(figure 16d,h), the calculations indicate a rapid change in stiffness, suggesting a change in the dominant instability (likely from ITG to KBM), but the gradient(s) at which this transition occurs depend strongly on the saturation rule. Like the differences in stiffness, SAT0 predicts the highest threshold for the switch to extremely stiff transport, and SAT2 the lowest. Given that SAT2 predicts the stiffest transport and lowest critical gradients, it is not surprising that it yields the lowest performance, or that SAT0 provides more optimistic predictions than SAT1 given its lower stiffness and equal or higher critical gradients. These differences are further magnified because any change at $\rho _{{\rm tor}} = 0.9$![]() propagates through the entire core region.
propagates through the entire core region.
These differences in saturation rule predictions, particularly for UCR-P, are somewhat surprising as significantly smaller differences are observed in the different saturation rules predictions of profiles in both current-day H-modes and other inductive burning-plasma scenario modelling (see, e.g. Mantica et al. Reference Mantica, Angioni, Bonanomi, Citrin, Grierson, Koechl, Mariani and Staebler2020; Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard and Candy2022b). One possible reason is to note that predicted fluxes for these scenarios are large enough, at all radii, that the differences in saturation rule stiffness matter, significantly impacting the ‘flux-matching’ $R/L_{{\rm Ti}}$![]() values. Even a modest 20 % difference in scale length at large radius can translate to a large increase in core temperature, density and fusion power. In contrast to this situation, many current-day H-mode scenarios, as well as the ITER baseline scenario and SPARC PRD sit at significantly lower gyroBohm-normalized fluxes, such that their predictions depend more on the predicted critical gradients than the stiffness of the transport above the threshold. Some examples of these differences are shown in figure 19, which compares the gyroBohm-normalized $Q_i$
values. Even a modest 20 % difference in scale length at large radius can translate to a large increase in core temperature, density and fusion power. In contrast to this situation, many current-day H-mode scenarios, as well as the ITER baseline scenario and SPARC PRD sit at significantly lower gyroBohm-normalized fluxes, such that their predictions depend more on the predicted critical gradients than the stiffness of the transport above the threshold. Some examples of these differences are shown in figure 19, which compares the gyroBohm-normalized $Q_i$![]() , $Q_e$
, $Q_e$![]() and $Q_{{\rm tot}}$
and $Q_{{\rm tot}}$![]() for a number of different plasmas. As seen in figure 19(a), the UCR-P gyroBohm-normalized ion energy flux $Q_i/Q_{gB}$
for a number of different plasmas. As seen in figure 19(a), the UCR-P gyroBohm-normalized ion energy flux $Q_i/Q_{gB}$![]() is roughly five times larger than the corresponding ITER baseline scenario and SPARC PRD values, and a full order of magnitude larger than two DIII-D H-mode plasmas with varied mixes of NBI and electron cyclotron heating (ECH) performed in an ITER baseline-like (IBS) shape (Grierson et al. Reference Grierson, Staebler, Solomon, McKee, Holland, Austin, Marinoni, Schmitz and Pinsker2018). However, the UCR-P normalized electron energy flux $Q_e/Q_{gB}$
is roughly five times larger than the corresponding ITER baseline scenario and SPARC PRD values, and a full order of magnitude larger than two DIII-D H-mode plasmas with varied mixes of NBI and electron cyclotron heating (ECH) performed in an ITER baseline-like (IBS) shape (Grierson et al. Reference Grierson, Staebler, Solomon, McKee, Holland, Austin, Marinoni, Schmitz and Pinsker2018). However, the UCR-P normalized electron energy flux $Q_e/Q_{gB}$![]() is comparable to the normalized ITER value, as well as the DIII-D H-mode with ECH heating. The UCR-SS scenario fluxes are similar in magnitude to the UCR-P, ITER and SPARC values at smaller radii but increase significantly (especially $Q_e$
is comparable to the normalized ITER value, as well as the DIII-D H-mode with ECH heating. The UCR-SS scenario fluxes are similar in magnitude to the UCR-P, ITER and SPARC values at smaller radii but increase significantly (especially $Q_e$![]() ) at the outer radii due to the strong off-axis heating and current drive in that use case. Finally, we note that although the UCR-P and UCR-SS fluxes are large relative to these other H-mode conditions, they are still an order of magnitude lower than a typical NBI-heated DIII-D L-mode discharge (White et al. Reference White, Schmitz, McKee, Holland, Peebles, Carter, Shafer, Austin, Burrell and Candy2008; Holland et al. Reference Holland, White, McKee, Shafer, Candy, Waltz, Schmitz and Tynan2009). Thus, there remains significant value in benchmarking reactor transport models against L-mode plasma scenarios as well as H-mode conditions to fully bracket the relevant reactor parameter space.
) at the outer radii due to the strong off-axis heating and current drive in that use case. Finally, we note that although the UCR-P and UCR-SS fluxes are large relative to these other H-mode conditions, they are still an order of magnitude lower than a typical NBI-heated DIII-D L-mode discharge (White et al. Reference White, Schmitz, McKee, Holland, Peebles, Carter, Shafer, Austin, Burrell and Candy2008; Holland et al. Reference Holland, White, McKee, Shafer, Candy, Waltz, Schmitz and Tynan2009). Thus, there remains significant value in benchmarking reactor transport models against L-mode plasma scenarios as well as H-mode conditions to fully bracket the relevant reactor parameter space.

Figure 19. Comparison of (a) $Q_i$![]() /$Q_{gB}$
/$Q_{gB}$![]() , (b) $Q_e$
, (b) $Q_e$![]() /$Q_{gB}$
/$Q_{gB}$![]() and (c) $Q_{{\rm tot}}$
and (c) $Q_{{\rm tot}}$![]() /$Q_{gB}$
/$Q_{gB}$![]() for different plasmas: UCR-P (—, blue), UCR-SS (—, red), SPARC PRD (—, purple), ITER baseline scenario (—, black), DIII-D IBS-NBI only (discharge 155196 3000 ms; — —, turquoise), DIII-D IBS-NBI+ECH (discharge 155196 2200 ms; — —, cyan) and DIII-D L-mode (discharge 128913 1500 ms; — —, green). The SPARC PRD profiles are taken from Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020), the ITER baseline profiles from Mantica et al. (Reference Mantica, Angioni, Bonanomi, Citrin, Grierson, Koechl, Mariani and Staebler2020), the DIII-D ITER baseline profiles from Grierson et al. (Reference Grierson, Staebler, Solomon, McKee, Holland, Austin, Marinoni, Schmitz and Pinsker2018), and the DIII-D L-mode profiles from White et al. (Reference White, Schmitz, McKee, Holland, Peebles, Carter, Shafer, Austin, Burrell and Candy2008) and Holland et al. (Reference Holland, White, McKee, Shafer, Candy, Waltz, Schmitz and Tynan2009).
for different plasmas: UCR-P (—, blue), UCR-SS (—, red), SPARC PRD (—, purple), ITER baseline scenario (—, black), DIII-D IBS-NBI only (discharge 155196 3000 ms; — —, turquoise), DIII-D IBS-NBI+ECH (discharge 155196 2200 ms; — —, cyan) and DIII-D L-mode (discharge 128913 1500 ms; — —, green). The SPARC PRD profiles are taken from Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020), the ITER baseline profiles from Mantica et al. (Reference Mantica, Angioni, Bonanomi, Citrin, Grierson, Koechl, Mariani and Staebler2020), the DIII-D ITER baseline profiles from Grierson et al. (Reference Grierson, Staebler, Solomon, McKee, Holland, Austin, Marinoni, Schmitz and Pinsker2018), and the DIII-D L-mode profiles from White et al. (Reference White, Schmitz, McKee, Holland, Peebles, Carter, Shafer, Austin, Burrell and Candy2008) and Holland et al. (Reference Holland, White, McKee, Shafer, Candy, Waltz, Schmitz and Tynan2009).
4. Implications
Although the results obtained from the development of these use cases is by no means a definitive final statement on what transport in a tokamak power plant (compact or otherwise) will look like, they do suggest some general properties of such a system that merit further consideration. In this section, we propose a heuristic model of transport in a D-T reactor informed by the results presented above, including both the D-D and D-T plasmas discussed in the previous section. Two metrics, based on the amount of collisional coupling and ratio of ion to electron turbulent transport, are then proposed for quantifying how well this model describes a given plasma. These proposed metrics are intended to be a first step in developing a quantitative means of characterizing how ‘reactor-like’ the expected core transport mechanisms in a plasma are, which can be used to help guide development of new experiments and facilities.
We begin by recalling that as shown in § 3, both UCR-P and UCR-SS exhibit significant energy transport through the ions even though electron heating is dominant for both use cases. Qualitatively, this situation is perhaps not surprising for a reactor plasma. In such a plasma, there must always be sufficient heating of the ions to ensure that they remain hot enough to sustain the fusion reactions. Furthermore, in an economically viable fusion pilot plant, the plasma must achieve a large enough $Q_{{\rm fusion}}$![]() that self-heating via the fusion products dominates over any auxiliary source(s), to overcome thermal conversion and recirculating power losses. Therefore, external sources cannot be relied on to heat the ions efficiently. Furthermore, because most of the alpha energy will be collisionally transferred to electrons at approximately 30 keV or lower (Stix Reference Stix1972), the plasma must be sufficiently well coupled that collisional transfer from the electrons to the thermal hydrogenic ions provides the needed heating to maintain the reactions. However, once this energy is in the core ions, it cannot be meaningfully dissipated by radiation, and so must be transported out towards the boundary for the plasma to remain stationary. This requirement translates to a need for significant turbulent transport of ion thermal energy (as neoclassical processes will be too small), and the fingerprint paradigm in turn constrains which microinstabilities can drive this ion thermal energy flux. In addition to the energy transport constraints, another likely constraint is the need for a turbulent electron and main ion particle pinch to drive peaked density profiles without significant core particle fuelling. This particle transport constraint is less stringent than the thermal transport constraint in that it is possible (at least at this heuristic level) to achieve an acceptable solution with little-to-no peaking by building upon a high enough pedestal density, as somewhat evidenced by the UCR-P scenario. However, as shown by the fixed-density predictions in § 2.3, density peaking provides a net boost to fusion performance and is virtually essential in steady-state plasmas to generate a significant bootstrap current fraction. Absent of deep core fuelling by pellet injection, this requirement for a pinch favours ITG and TEM turbulence as the dominant core transport mechanisms over KBM turbulence. Localized regions of dominant KBM turbulence may still exist (e.g. potentially in the outer region around $\rho _{{\rm tor}} = 0.8$
that self-heating via the fusion products dominates over any auxiliary source(s), to overcome thermal conversion and recirculating power losses. Therefore, external sources cannot be relied on to heat the ions efficiently. Furthermore, because most of the alpha energy will be collisionally transferred to electrons at approximately 30 keV or lower (Stix Reference Stix1972), the plasma must be sufficiently well coupled that collisional transfer from the electrons to the thermal hydrogenic ions provides the needed heating to maintain the reactions. However, once this energy is in the core ions, it cannot be meaningfully dissipated by radiation, and so must be transported out towards the boundary for the plasma to remain stationary. This requirement translates to a need for significant turbulent transport of ion thermal energy (as neoclassical processes will be too small), and the fingerprint paradigm in turn constrains which microinstabilities can drive this ion thermal energy flux. In addition to the energy transport constraints, another likely constraint is the need for a turbulent electron and main ion particle pinch to drive peaked density profiles without significant core particle fuelling. This particle transport constraint is less stringent than the thermal transport constraint in that it is possible (at least at this heuristic level) to achieve an acceptable solution with little-to-no peaking by building upon a high enough pedestal density, as somewhat evidenced by the UCR-P scenario. However, as shown by the fixed-density predictions in § 2.3, density peaking provides a net boost to fusion performance and is virtually essential in steady-state plasmas to generate a significant bootstrap current fraction. Absent of deep core fuelling by pellet injection, this requirement for a pinch favours ITG and TEM turbulence as the dominant core transport mechanisms over KBM turbulence. Localized regions of dominant KBM turbulence may still exist (e.g. potentially in the outer region around $\rho _{{\rm tor}} = 0.8$![]() between the foot of the ITB and top of the pedestal in UCR-SS), but likely must be modest compared with the volume controlled by ITG and TEM modes.
between the foot of the ITB and top of the pedestal in UCR-SS), but likely must be modest compared with the volume controlled by ITG and TEM modes.
Closer to the boundary, increasing radiation and rapid conduction along SOL field lines will predominantly cool the electrons over ions, leading to a transition from $T_e > T_i$![]() in the core to $T_e < T_i$
in the core to $T_e < T_i$![]() near the edge, although the degree of separation of temperatures in the pedestal and edge will also depend sensitively on the collisionality and coupling in that region. This transition also allows energy which had been coupled into the ions to now be collisionally transferred (back) into the electrons, where it may potentially be radiated before being transported across the separatrix. A change in the relative magnitudes in the ion and electron thermal transport in this regime also implies that the mix of microinstabilities providing the transport will change accordingly. Neoclassical contributions may again become important depending on what values parameters such as the collisionality reach in the pedestal. However, the need for the main ion particle pinch in the pedestal is even larger than in the core for a compact reactor, as the inherently high density required for these plasmas implies a high neutral opacity and minimal capability for core fuelling via edge gas puffing. A cartoon visualization of these dynamics is sketched in figure 20. While obviously quite qualitative, it suggests a potentially useful heuristic picture of competing transport effects in a D-T reactor, likely applicable even beyond compact tokamaks.
near the edge, although the degree of separation of temperatures in the pedestal and edge will also depend sensitively on the collisionality and coupling in that region. This transition also allows energy which had been coupled into the ions to now be collisionally transferred (back) into the electrons, where it may potentially be radiated before being transported across the separatrix. A change in the relative magnitudes in the ion and electron thermal transport in this regime also implies that the mix of microinstabilities providing the transport will change accordingly. Neoclassical contributions may again become important depending on what values parameters such as the collisionality reach in the pedestal. However, the need for the main ion particle pinch in the pedestal is even larger than in the core for a compact reactor, as the inherently high density required for these plasmas implies a high neutral opacity and minimal capability for core fuelling via edge gas puffing. A cartoon visualization of these dynamics is sketched in figure 20. While obviously quite qualitative, it suggests a potentially useful heuristic picture of competing transport effects in a D-T reactor, likely applicable even beyond compact tokamaks.

Figure 20. Sketch of the proposed heuristic power flow model of a well-coupled reactor plasma.
To make this characterization more quantitative, it is useful to identify and calculate metrics for the proposed reactor plasma properties. A natural measure of the coupling is to determine the ratio of the energy confinement time $\tau _E$![]() to the collisional exchange time $\tau _{{\rm exch}}$
to the collisional exchange time $\tau _{{\rm exch}}$![]() , analogous to the approach used by Ryter et al. (Reference Ryter, Orte, Kurzan, McDermott, Tardini, Viezzer, Bernert and Fischer2014). Functionally, if $\tau _E/\tau _{{\rm exch}}$
, analogous to the approach used by Ryter et al. (Reference Ryter, Orte, Kurzan, McDermott, Tardini, Viezzer, Bernert and Fischer2014). Functionally, if $\tau _E/\tau _{{\rm exch}}$![]() is much larger than one, we can argue the plasma is well coupled, as the time scale for energy exchange and equilibration is much shorter than the time scale for energy to leave the system. In the opposite limit ($\tau _E/\tau _{{\rm exch}}\ll 1$
is much larger than one, we can argue the plasma is well coupled, as the time scale for energy exchange and equilibration is much shorter than the time scale for energy to leave the system. In the opposite limit ($\tau _E/\tau _{{\rm exch}}\ll 1$![]() ), energy leaves the system much more rapidly than it is exchanged between species, such that ions and electrons are effectively decoupled. Quantifying the relative magnitudes of ion versus electron thermal transport can be done in multiple ways. At a simple level, one can simply calculate the relative ratios of net conducted power through the ions and electrons. However, determining what is the dominant turbulence instability that controls core transport requires digging a little deeper. Multiple approaches are possible, but here we propose one based on making contact with the fingerprint paradigm by examining ratios of turbulent ion-to-electron thermal diffusivities. To do so, we first subtract off any convective contributions to the energy fluxes, which are by definition equal to zero for UCR-P and UCR-SS but potentially finite for other plasmas. We then subtract the neoclassical contributions to the conducted energy fluxes (as calculated by NEO) and express the remaining turbulent heat fluxes in terms of thermal diffusivities $\chi _{i/e}^{{\rm turb}} = Q_{i/e} /(-n_{i/e} \,{\rm d}T_{i/e}/{\rm d}r_{{\rm min}})$
), energy leaves the system much more rapidly than it is exchanged between species, such that ions and electrons are effectively decoupled. Quantifying the relative magnitudes of ion versus electron thermal transport can be done in multiple ways. At a simple level, one can simply calculate the relative ratios of net conducted power through the ions and electrons. However, determining what is the dominant turbulence instability that controls core transport requires digging a little deeper. Multiple approaches are possible, but here we propose one based on making contact with the fingerprint paradigm by examining ratios of turbulent ion-to-electron thermal diffusivities. To do so, we first subtract off any convective contributions to the energy fluxes, which are by definition equal to zero for UCR-P and UCR-SS but potentially finite for other plasmas. We then subtract the neoclassical contributions to the conducted energy fluxes (as calculated by NEO) and express the remaining turbulent heat fluxes in terms of thermal diffusivities $\chi _{i/e}^{{\rm turb}} = Q_{i/e} /(-n_{i/e} \,{\rm d}T_{i/e}/{\rm d}r_{{\rm min}})$![]() . In calculating the ion thermal diffusivity, the fast alpha particles are neglected and all thermal ions are taken to have the same temperature; $n_i$
. In calculating the ion thermal diffusivity, the fast alpha particles are neglected and all thermal ions are taken to have the same temperature; $n_i$![]() is the total thermal ion number density. Note that by focusing specifically on the turbulent diffusivities rather than total values, we are able to better discriminate between plasmas with and without significant neoclassical contributions. Such a distinction is necessary for some current-day plasmas as neoclassical and turbulent transport have very different scalings when projecting to reactor conditions, due to the much stronger collisionality dependence of neoclassical fluxes. Figure 21 plots the coupling metric versus the ratio of ion to electron heating (from both fusion and external sources), as well as the ratio of fluxes $\left \langle Q_i/Q_e \right \rangle _{0.9}$
is the total thermal ion number density. Note that by focusing specifically on the turbulent diffusivities rather than total values, we are able to better discriminate between plasmas with and without significant neoclassical contributions. Such a distinction is necessary for some current-day plasmas as neoclassical and turbulent transport have very different scalings when projecting to reactor conditions, due to the much stronger collisionality dependence of neoclassical fluxes. Figure 21 plots the coupling metric versus the ratio of ion to electron heating (from both fusion and external sources), as well as the ratio of fluxes $\left \langle Q_i/Q_e \right \rangle _{0.9}$![]() and thermal diffusivities $\left \langle \chi _i^{{\rm turb}}/\chi _e^{{\rm turb}} \right \rangle _{0.9}$
and thermal diffusivities $\left \langle \chi _i^{{\rm turb}}/\chi _e^{{\rm turb}} \right \rangle _{0.9}$![]() . Here the $\left \langle \cdots \right \rangle _{0.9}$
. Here the $\left \langle \cdots \right \rangle _{0.9}$![]() brackets denote a volume-weighted average of the quantity over $0 \le \rho _{{\rm tor}} \le 0.9$
brackets denote a volume-weighted average of the quantity over $0 \le \rho _{{\rm tor}} \le 0.9$![]() . Note that $\tau _{{\rm exch}}$
. Note that $\tau _{{\rm exch}}$![]() is also a volume-averaged quantity.
is also a volume-averaged quantity.

Figure 21. The coupling metric $\tau _E/\left \langle \tau _{{\rm exch}} \right \rangle _{0.9}$![]() as a function of (a) the heating ratio $P_i^{{\rm heat}}/P_e^{{\rm heat}}$
as a function of (a) the heating ratio $P_i^{{\rm heat}}/P_e^{{\rm heat}}$![]() , (b) the flux ratio $\left \langle Q_i/Q_e \right \rangle _{0.9}$
, (b) the flux ratio $\left \langle Q_i/Q_e \right \rangle _{0.9}$![]() and (c) the turbulent thermal diffusivity ratio $\left \langle \chi _i^{{\rm turb}}/\chi _e^{{\rm turb}} \right \rangle _{0.9}$
and (c) the turbulent thermal diffusivity ratio $\left \langle \chi _i^{{\rm turb}}/\chi _e^{{\rm turb}} \right \rangle _{0.9}$![]() for the range of scenarios and discharges considered in § 4.
for the range of scenarios and discharges considered in § 4.
As can be seen, the various H-mode plasmas all exhibit coupling metrics $\tau _E/\left \langle \tau _{{\rm exch}} \right \rangle _{0.9} > 1$![]() , although there is a factor of six variation from the weakest-coupled plasma (the DIII-D ITER baseline scenario plasma with electron cyclotron heating) and the strongest-coupled plasma (UCR-P). Although all but one of the plasmas (the NBI-only DIII-D IBS) are predominantly electron heated (figure 21a), they all exhibit significant ion thermal transport. The choice of transport process metric ($\left \langle Q_i/Q_e \right \rangle _{0.9}$
, although there is a factor of six variation from the weakest-coupled plasma (the DIII-D ITER baseline scenario plasma with electron cyclotron heating) and the strongest-coupled plasma (UCR-P). Although all but one of the plasmas (the NBI-only DIII-D IBS) are predominantly electron heated (figure 21a), they all exhibit significant ion thermal transport. The choice of transport process metric ($\left \langle Q_i/Q_e \right \rangle _{0.9}$![]() or $\left \langle \chi _i^{{\rm turb}}/\chi _e^{{\rm turb}} \right \rangle _{0.9}$
or $\left \langle \chi _i^{{\rm turb}}/\chi _e^{{\rm turb}} \right \rangle _{0.9}$![]() ) yields two slightly different orderings of the plasmas. In either case, essentially linear scaling of coupling with $\left \langle Q_i/Q_e \right \rangle _{0.9}$
) yields two slightly different orderings of the plasmas. In either case, essentially linear scaling of coupling with $\left \langle Q_i/Q_e \right \rangle _{0.9}$![]() or $\left \langle \chi _i^{{\rm turb}}/\chi _e^{{\rm turb}}\right \rangle _{0.9}$
or $\left \langle \chi _i^{{\rm turb}}/\chi _e^{{\rm turb}}\right \rangle _{0.9}$![]() is observed for the H-mode plasmas, suggesting that the actual mix of turbulent transport processes is changing. The largest change is for the DIII-D ITER baseline discharge with both NBI and ECH heating, as although its volume averaged core $\left \langle Q_i/Q_e \right \rangle _{0.9}$
is observed for the H-mode plasmas, suggesting that the actual mix of turbulent transport processes is changing. The largest change is for the DIII-D ITER baseline discharge with both NBI and ECH heating, as although its volume averaged core $\left \langle Q_i/Q_e \right \rangle _{0.9}$![]() slightly above two, its ratio of turbulent diffusivities is slightly less than one. For this plasma, the flux ratio result is skewed by the fact that although the off-axis ECH leads to $Q_e \sim 2Q_i$
slightly above two, its ratio of turbulent diffusivities is slightly less than one. For this plasma, the flux ratio result is skewed by the fact that although the off-axis ECH leads to $Q_e \sim 2Q_i$![]() for $\rho _{{\rm tor}} > 0.4$
for $\rho _{{\rm tor}} > 0.4$![]() , there is near zero electron energy flow inside this location such that volume average is strongly weighted by the large $Q_i/Q_e$
, there is near zero electron energy flow inside this location such that volume average is strongly weighted by the large $Q_i/Q_e$![]() at the inner radii. It is also noteworthy that for UCR-P $\left \langle \chi _i^{{\rm turb}}/\chi _e^{{\rm turb}}\right \rangle _{0.9} = 3.3$
at the inner radii. It is also noteworthy that for UCR-P $\left \langle \chi _i^{{\rm turb}}/\chi _e^{{\rm turb}}\right \rangle _{0.9} = 3.3$![]() , whereas it is only 1.0 for UCR-SS, consistent with increased fraction of electron transport and higher relative importance for short-wavelength modes in UCR-SS. It is also interesting to note that the DIII-D H-mode plasma with only balanced NBI is much closer in both metrics to ITER than the corresponding DIII-D plasma with ECH and reduced NBI heating, which is closest to UCR-SS. This result is actually quite non-trivial as it suggests that the impact of trying to mimic the alpha heating in the DIII-D plasma by increased ECH power actually took the plasma core further away from the transport regime of interest relative to simply using balanced NBI heating. However, it appears that this heating change provides a closer match to an AT reactor-like plasma than the nominal inductive plasma scenario being targeted in the experiment, consistent with significant off-axis RF electron heating being applied in both plasmas. Finally, by these metrics, the closest plasma to UCR-P is predicted to be the SPARC PRD, which sits more or less halfway between ITER and UCR-P. As with many other elements of the modelling and analysis presented in this paper, the specific choices for these metrics are not unique or necessarily optimal, but they will hopefully stimulate new ways of analysing and comparing current and future plasmas’ reactor relevance.
, whereas it is only 1.0 for UCR-SS, consistent with increased fraction of electron transport and higher relative importance for short-wavelength modes in UCR-SS. It is also interesting to note that the DIII-D H-mode plasma with only balanced NBI is much closer in both metrics to ITER than the corresponding DIII-D plasma with ECH and reduced NBI heating, which is closest to UCR-SS. This result is actually quite non-trivial as it suggests that the impact of trying to mimic the alpha heating in the DIII-D plasma by increased ECH power actually took the plasma core further away from the transport regime of interest relative to simply using balanced NBI heating. However, it appears that this heating change provides a closer match to an AT reactor-like plasma than the nominal inductive plasma scenario being targeted in the experiment, consistent with significant off-axis RF electron heating being applied in both plasmas. Finally, by these metrics, the closest plasma to UCR-P is predicted to be the SPARC PRD, which sits more or less halfway between ITER and UCR-P. As with many other elements of the modelling and analysis presented in this paper, the specific choices for these metrics are not unique or necessarily optimal, but they will hopefully stimulate new ways of analysing and comparing current and future plasmas’ reactor relevance.
5. Conclusions and future work
In this paper, we have presented the first results of a new integrated modelling study of core D-T tokamak plasmas at conditions representative of a potential compact reactor, undertaken to better understand and quantify the core plasma transport and stability in such a facility. Within the assumptions used in our modelling, we find that in a $R_0 = 4 \,\mathrm {m}$![]() , $B_0 = 8 \,\mathrm {T}$
, $B_0 = 8 \,\mathrm {T}$![]() device, both the pulsed UCR-P and steady-state UCR-SS plasmas can generate sufficient fusion power to generate 200 MW or more net electric power. However, we emphasize that these assumptions are significant and extensive, and that these use case results should only be taken as a possible starting point for more detailed transport and confinement studies, especially the future development and verification of reduced transport models.
device, both the pulsed UCR-P and steady-state UCR-SS plasmas can generate sufficient fusion power to generate 200 MW or more net electric power. However, we emphasize that these assumptions are significant and extensive, and that these use case results should only be taken as a possible starting point for more detailed transport and confinement studies, especially the future development and verification of reduced transport models.
The most important conclusion of this study is that the predicted performance of the scenarios is enormously dependent on the choice of transport model used. When keeping most assumed parameters such as device size, field and shape fixed, the predicted range of scenario outcomes can effectively range from runaway ignition to radiative collapse of the plasma, depending on whether the TGLF SAT0, SAT1 or SAT2 model is used. More realistically, this finding suggests that an FPP or other strongly burning plasma facility designed using one of these saturation rules is likely to have some significantly different properties than a facility using a different saturation rule. These differences arise from fundamentally different levels of transport stiffness predicted by each model, even though they have very similar critical gradients, as shown in figures 17 and 18. As shown in figure 19, UCR-P and UCR-SS have gyroBohm normalized fluxes up to an order of magnitude larger than current-day H-modes, or what is expected in the ITER baseline scenario and SPARC PRD. So while these other H-mode plasmas with relatively low fluxes inherently sit close to the critical gradient, the larger fluxes in UCR-P and UCR-SS move them further up the stiffness curve so to speak, magnifying the differences between the saturation rules. These larger fluxes are a natural feature of a reactor plasma, which must not only be burning ($Q_{{\rm fusion}} = 5 - 10$![]() ) but burning strongly enough for the fusion generated to overcome thermal efficiencies and recirculating power limitations. Thus in UCR-P and UCR-SS, $Q_{{\rm fusion}} = 27.3$
) but burning strongly enough for the fusion generated to overcome thermal efficiencies and recirculating power limitations. Thus in UCR-P and UCR-SS, $Q_{{\rm fusion}} = 27.3$![]() and 12.9, respectively, roughly a factor of two larger than the corresponding ITER baseline inductive and steady-state scenarios ($Q_{{\rm fusion}} = 15$
and 12.9, respectively, roughly a factor of two larger than the corresponding ITER baseline inductive and steady-state scenarios ($Q_{{\rm fusion}} = 15$![]() and 5, respectively) (ITER Physics Basis Editors et al. 1999). As these different saturation rules will translate to significantly different reactor designs, likely with significantly different levels of economic cost and attractiveness, further study and verification in this reactor plasma regime is essential. Ideally, these predictions would also be validated against experimental data, but it is not clear how well existing or proposed pre-reactor devices can access this regime or if a new facility such as EXCITE (FESAC 2020; Menard et al. Reference Menard, Grierson, Brown, Rana, Zhai, Poli, Maingi, Guttenfelder and Snyder2022) would be needed to study these conditions outside of a reactor. In any case, these studies must go beyond examining the thermal transport stiffness to also investigating how the particle transport of all species will scale and vary in this regime. To confidently predict a fully self-consistent plasma solution that satisfies the core-edge integration constraints, accurate prediction of main-ion density peaking in source-free, low collisionality, potentially electromagnetic regimes is essential, as are the profiles of radiative impurity ions. This need is even more stringent for any reactor which will rely heavily upon the bootstrap current, as accurate density gradient profiles are required for that calculation. A promising recent result is that of Howard et al. (Reference Howard, Rodriguez-Fernandez, Holland, Rice, Greenwald, Candy and Sciortino2021b), who find core neoclassical impurity transport in SPARC to be negligible and that gyrokinetic simulations of SPARC plasmas do not predict dangerous levels of core impurity accumulation. Similar results were found for the ITER baseline inductive scenario by Angioni et al. (Reference Angioni, Bilato, Casson, Fable, Mantica, Odstrcil and Valisa2017) and Grierson et al. (Reference Grierson, Staebler, Solomon, McKee, Holland, Austin, Marinoni, Schmitz and Pinsker2018), particularly with regards to the dominance of turbulent over neoclassical transport. Whether this trend holds over a larger range of conditions, and in particular for UCR-SS like plasmas, is currently under investigation. Evidence for the possibility of a significant rotation pinch in this regime should also be searched for, as an intrinsically forming equilibrium shear flow in the core (even just the outer radii) would almost certainly boost plasma performance and stability.
and 5, respectively) (ITER Physics Basis Editors et al. 1999). As these different saturation rules will translate to significantly different reactor designs, likely with significantly different levels of economic cost and attractiveness, further study and verification in this reactor plasma regime is essential. Ideally, these predictions would also be validated against experimental data, but it is not clear how well existing or proposed pre-reactor devices can access this regime or if a new facility such as EXCITE (FESAC 2020; Menard et al. Reference Menard, Grierson, Brown, Rana, Zhai, Poli, Maingi, Guttenfelder and Snyder2022) would be needed to study these conditions outside of a reactor. In any case, these studies must go beyond examining the thermal transport stiffness to also investigating how the particle transport of all species will scale and vary in this regime. To confidently predict a fully self-consistent plasma solution that satisfies the core-edge integration constraints, accurate prediction of main-ion density peaking in source-free, low collisionality, potentially electromagnetic regimes is essential, as are the profiles of radiative impurity ions. This need is even more stringent for any reactor which will rely heavily upon the bootstrap current, as accurate density gradient profiles are required for that calculation. A promising recent result is that of Howard et al. (Reference Howard, Rodriguez-Fernandez, Holland, Rice, Greenwald, Candy and Sciortino2021b), who find core neoclassical impurity transport in SPARC to be negligible and that gyrokinetic simulations of SPARC plasmas do not predict dangerous levels of core impurity accumulation. Similar results were found for the ITER baseline inductive scenario by Angioni et al. (Reference Angioni, Bilato, Casson, Fable, Mantica, Odstrcil and Valisa2017) and Grierson et al. (Reference Grierson, Staebler, Solomon, McKee, Holland, Austin, Marinoni, Schmitz and Pinsker2018), particularly with regards to the dominance of turbulent over neoclassical transport. Whether this trend holds over a larger range of conditions, and in particular for UCR-SS like plasmas, is currently under investigation. Evidence for the possibility of a significant rotation pinch in this regime should also be searched for, as an intrinsically forming equilibrium shear flow in the core (even just the outer radii) would almost certainly boost plasma performance and stability.
Fortunately, the second major conclusion of the work presented here provides some guidance on how to further focus investigations of reactor transport. As illustrated by the heuristic picture presented in § 4 and shown in figure 20, basic considerations of transport in a reactor-relevant plasma lead to a situation where the ions carry significant thermal transport, which in turn requires long-wavelength instabilities such as ITG, TEM or KBM modes to be active to drive this transport. The desire (if not need) for a core density pinch further weights towards ITG and TEM modes as the dominant turbulent transport drivers rather than KBMs. This picture does not rule out contributions from ETG or MTMs, but does suggest they are more likely to be modest complements to the long-wavelength turbulence rather than dominant transport drivers on their own. This argument is of course a simplified one, and phenomena such as nonlinear cross-scale interactions (e.g. enhancement of long-wavelength fluctuations by energy transfer from short wavelengths, or interactions between drift-wave turbulence and energetic-particle driven modes Citrin et al. Reference Citrin, Garcia, Gorler, Jenko, Mantica, Told, Bourdelle, Hatch, Hogeweij and Johnson2014; Mazzi et al. Reference Mazzi, Garcia, Zarzoso, Kazakov, Ongena, Dreval, Nocente, Štancar, Szepesi and Eriksson2022; Siena et al. Reference Siena, Bilato, Görler, Poli, Navarro, Jarema and Jenko2022) could play an important role here. Therefore verifying the expected fingerprints of these modes in reactor plasma conditions, as well as testing possible nonlinear interactions between different scales and instabilities, should also be fundamental components of the future studies proposed above.
It would also be quite valuable to assess the generality of the heuristic picture of reactor transport presented in § 4. In particular, is there an equivalent self-consistent picture of a weakly coupled hot ion (robustly $T_i > T_e$![]() ) plasma dominated by electron thermal transport? One can, in principle, envision elements of such a regime, in which a very hot plasma for which the ITG mode is stabilized (e.g. via strong Shafranov shift, or by some means of efficient shear flow generation) but TEMs and/or KBMs are not, while also satisfying global $\beta$
) plasma dominated by electron thermal transport? One can, in principle, envision elements of such a regime, in which a very hot plasma for which the ITG mode is stabilized (e.g. via strong Shafranov shift, or by some means of efficient shear flow generation) but TEMs and/or KBMs are not, while also satisfying global $\beta$![]() limits and pedestal/edge conditions compatible with an acceptable exhaust solution. In the absence of such a counter-example, the strongly coupled plasma picture proposed here suggests some natural quantities for metrics that can be used to compare different reactor scenarios, as well as assess the reactor relevance of current-day plasmas. The first, and most obvious, is to define some sort of coupling parameter like the ratio of energy confinement to exchange time scales, as was used in figure 21. The second would address the nature of the transport in the core, either as a straightforward ratio of energy fluxes or more specifically as a ratio of turbulent diffusivities. These metrics (or some variations thereon) could be used alongside other standard dimensionless parameters such as $H_{98(y,2)}$
limits and pedestal/edge conditions compatible with an acceptable exhaust solution. In the absence of such a counter-example, the strongly coupled plasma picture proposed here suggests some natural quantities for metrics that can be used to compare different reactor scenarios, as well as assess the reactor relevance of current-day plasmas. The first, and most obvious, is to define some sort of coupling parameter like the ratio of energy confinement to exchange time scales, as was used in figure 21. The second would address the nature of the transport in the core, either as a straightforward ratio of energy fluxes or more specifically as a ratio of turbulent diffusivities. These metrics (or some variations thereon) could be used alongside other standard dimensionless parameters such as $H_{98(y,2)}$![]() and $\beta _{N}$
and $\beta _{N}$![]() to characterize different possible solutions.
to characterize different possible solutions.
Finally, as we have emphasized throughout the paper, there are many possible alternate choices in the stating assumptions which could be pursued to improve predicted performance, such as varying the relative amounts of working gasses and/or operating density. Within the context of the ITEP challenge discussed in § 1, using those actuators to raise or lower the use case $P_{{\rm sep}}$![]() to values closer to $P_{{\rm LH}}$
to values closer to $P_{{\rm LH}}$![]() while maintaining core performance would be an important next step. Further studies of transport in the pedestal and scrape-off layer are possible, but would require a more sophisticated engineering analysis to specify the magnetic geometry beyond the separatrix. In this vein, more detailed predictions of impurity concentration that go beyond the constant $Z_{{\rm eff}}$
while maintaining core performance would be an important next step. Further studies of transport in the pedestal and scrape-off layer are possible, but would require a more sophisticated engineering analysis to specify the magnetic geometry beyond the separatrix. In this vein, more detailed predictions of impurity concentration that go beyond the constant $Z_{{\rm eff}}$![]() assumed here would be particularly enlightening, as the trade-offs between core dilution, near-edge and SOL radiation, and collisionality changes are complex and non-trivial. While existing transport models can predict core impurity fluxes at both the trace and non-trace levels, the largest hurdle is in predicting the relative concentration levels of different species at the pedestal top, which sets the effective core boundary condition. However, doing so would in turn require predicting multispecies concentrations and transport through the pedestal/near-edge and SOL regions, which introduces significant uncertainties and challenges for accurately capturing various particle source and sink terms, as well as tracking many charge states, and for which a robust predictive capability does not yet exist. Such a capability would be a natural component of predictive near-edge transport models for ELM-free regimes, as discussed in § 2.1. Likewise, an improved treatment of the auxiliary RF heating to more rigorously specify particular wave frequencies, deposition profiles, efficiencies etc. is also possible with additional design choices, as well as investigation of deep pellet fuelling utility. In particular, the questions of achievable $\eta _{{\rm CD}}$
assumed here would be particularly enlightening, as the trade-offs between core dilution, near-edge and SOL radiation, and collisionality changes are complex and non-trivial. While existing transport models can predict core impurity fluxes at both the trace and non-trace levels, the largest hurdle is in predicting the relative concentration levels of different species at the pedestal top, which sets the effective core boundary condition. However, doing so would in turn require predicting multispecies concentrations and transport through the pedestal/near-edge and SOL regions, which introduces significant uncertainties and challenges for accurately capturing various particle source and sink terms, as well as tracking many charge states, and for which a robust predictive capability does not yet exist. Such a capability would be a natural component of predictive near-edge transport models for ELM-free regimes, as discussed in § 2.1. Likewise, an improved treatment of the auxiliary RF heating to more rigorously specify particular wave frequencies, deposition profiles, efficiencies etc. is also possible with additional design choices, as well as investigation of deep pellet fuelling utility. In particular, the questions of achievable $\eta _{{\rm CD}}$![]() and plasma access for existing RF source technologies should be much better quantified. This refined analysis would be particularly valuable to the UCR-SS plasma, as it depends much more sensitively on the details of the fuelling and heating sources than UCR-P does.
and plasma access for existing RF source technologies should be much better quantified. This refined analysis would be particularly valuable to the UCR-SS plasma, as it depends much more sensitively on the details of the fuelling and heating sources than UCR-P does.
Acknowledgements
The authors thank E.A. Belli, W. Boyes, J. Candy, M. Knolker, O. Meneghini, S.P. Smith, P. Snyder, G.M. Staebler, M.W. Shafer and D. Weisberg for helpful conversations, as well as P. Snyder for assistance with the EPED calculations, A. Turnbull for assistance with the GATO calculations, D. Weisberg for assistance with preparation of Fig. A1, and O. Meneghini and S.P. Smith for OMFIT support and assistance.
Editor Alex Schekochihin thanks the referees for their advice in evaluating this article.
Funding
This research was performed as part of the Advanced Tokamak Modeling SciDAC project, supported by the US Department of Energy, Office of Science, Office of Fusion Energy Sciences under Award DE-SC0018287. Additional support was provided by DOE Awards DE-FG02-95ER54309, DE-SC0017992, and DE-SC0014264. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a US Department of Energy Office of Science User Facility operated under Contract No. DE-AC02-05CH11231.
Declaration of interests
The authors report no conflict of interest.
Data availability
All supporting data are available from the lead author upon reasonable request. All GACODE results shown in this paper were calculated using source code corresponding to git hash 9a4a642c (committed to the GitHub repository on February 22, 2022).
Appendix A. System power flow modelling
While the focus of this paper is on the modelling of the core plasma in a tokamak FPP, a model of overall plant efficiency and power flow is required to translate the plasma performance into an assessment of actual electric power generated. A schematic visualization of such a power flow model is shown in figure 22. The starting point for the analysis is the plasma itself in the bottom left corner of figure 22, which produces $P_{{\rm fusion}}$![]() MW of energy when $P_{{\rm aux}}$
MW of energy when $P_{{\rm aux}}$![]() MW of energy are absorbed by the plasma; accordingly, $Q_{{\rm fusion}} = P_{{\rm fusion}}/P_{{\rm aux}}$
MW of energy are absorbed by the plasma; accordingly, $Q_{{\rm fusion}} = P_{{\rm fusion}}/P_{{\rm aux}}$![]() . For a D-T plasma, 80 % of this energy is released as 14.1 MeV neutrons that are absorbed by the breeding blanket. When these neutrons are captured by $\mathrm {Li}^6$
. For a D-T plasma, 80 % of this energy is released as 14.1 MeV neutrons that are absorbed by the breeding blanket. When these neutrons are captured by $\mathrm {Li}^6$![]() atoms to generate tritium, an additional 4.8 MeV of energy is released, leading to a 34 % enhancement of the absorbed neutron power. This enhancement is balanced against the at best fractional recovery of the absorbed heating power $P_{{\rm aux}}$
atoms to generate tritium, an additional 4.8 MeV of energy is released, leading to a 34 % enhancement of the absorbed neutron power. This enhancement is balanced against the at best fractional recovery of the absorbed heating power $P_{{\rm aux}}$![]() and remaining 20 % of the D-T reaction energy which also serves to heat the plasma. These sources of thermal energy are transformed into electric power via e.g. a steam cycle with an efficiency $\eta _{{\rm th}}$
and remaining 20 % of the D-T reaction energy which also serves to heat the plasma. These sources of thermal energy are transformed into electric power via e.g. a steam cycle with an efficiency $\eta _{{\rm th}}$![]() . Thus, the total electric power generated is given by
. Thus, the total electric power generated is given by
where $\eta _{{\rm recov}}$![]() is the fraction of thermal heat recovered directly from the tokamak vessel (e.g. via cooling of divertor and first wall) and $\eta _{{\rm blanket}}$
is the fraction of thermal heat recovered directly from the tokamak vessel (e.g. via cooling of divertor and first wall) and $\eta _{{\rm blanket}}$![]() is the enhancement of the neutron power in the blanket. Values of $\eta _{{\rm blanket}} < 1.34$
is the enhancement of the neutron power in the blanket. Values of $\eta _{{\rm blanket}} < 1.34$![]() are typically used to represent incomplete capture of the neutron energy and other possible inefficiencies.
are typically used to represent incomplete capture of the neutron energy and other possible inefficiencies.

Figure 22. Schematic of overall power flow in a fusion power plant, illustrated with UCR-P values. Adapted with permission from Buttery et al. (Reference Buttery, Park, McClenaghan, Weisberg, Canik, Ferron, Garofalo, Holcomb, Leuer and Snyder2021).
To determine the net electric power $P_{{\rm net}}$![]() generated, the recirculating power needed to provide the auxiliary heating must be subtracted, as well as the balance-of-plant power required for operation of the facility. The total ‘wallplug’ power $P_{{\rm wall}}$
generated, the recirculating power needed to provide the auxiliary heating must be subtracted, as well as the balance-of-plant power required for operation of the facility. The total ‘wallplug’ power $P_{{\rm wall}}$![]() needed to provide $P_{{\rm aux}}$
needed to provide $P_{{\rm aux}}$![]() MW of absorbed plasma power is given by $P_{{\rm aux}} = \eta _{{\rm aux}} P_{{\rm wall}} = \eta _{{\rm abs}}\eta _{{\rm wallplug}} P_{{\rm wall}}$
MW of absorbed plasma power is given by $P_{{\rm aux}} = \eta _{{\rm aux}} P_{{\rm wall}} = \eta _{{\rm abs}}\eta _{{\rm wallplug}} P_{{\rm wall}}$![]() , where $\eta _{{\rm abs}}$
, where $\eta _{{\rm abs}}$![]() is the fraction of injected power absorbed by the plasma and $\eta _{{\rm wallplug}}$
is the fraction of injected power absorbed by the plasma and $\eta _{{\rm wallplug}}$![]() is the efficiency by which the heating source (e.g. a gyrotron or neutral beam source) transforms input electricity into RF wave or beam power. Accurately determining the balance-of-plant power $P_{{\rm BOP}}$
is the efficiency by which the heating source (e.g. a gyrotron or neutral beam source) transforms input electricity into RF wave or beam power. Accurately determining the balance-of-plant power $P_{{\rm BOP}}$![]() requires significant engineering and facility analysis well beyond what is considered here. Instead, we simply estimate that $P_{{\rm BOP}} = \eta _{{\rm BOP}} P_{{\rm elec}}$
requires significant engineering and facility analysis well beyond what is considered here. Instead, we simply estimate that $P_{{\rm BOP}} = \eta _{{\rm BOP}} P_{{\rm elec}}$![]() i.e. a simple fraction of the total electric power generated, similar to what some other studies have assumed. Combining these ‘costs’ together gives a relation for expressing $P_{{\rm net}}$
i.e. a simple fraction of the total electric power generated, similar to what some other studies have assumed. Combining these ‘costs’ together gives a relation for expressing $P_{{\rm net}}$![]() as a function of $Q_{{\rm fusion}}$
as a function of $Q_{{\rm fusion}}$![]() , $P_{{\rm aux}}$
, $P_{{\rm aux}}$![]() and various efficiencies:
and various efficiencies:
For this work, we take $\eta _{{\rm BOP}} = 0.1$![]() , $\eta _{{\rm th}} = 0.35$
, $\eta _{{\rm th}} = 0.35$![]() , $\eta _{{\rm blanket}} = 1.25$
, $\eta _{{\rm blanket}} = 1.25$![]() , $\eta _{{\rm recov}} = 0.5$
, $\eta _{{\rm recov}} = 0.5$![]() , $\eta _{{\rm abs}} = 0.8$
, $\eta _{{\rm abs}} = 0.8$![]() and $\eta _{{\rm wallplug}} = 0.5$
and $\eta _{{\rm wallplug}} = 0.5$![]() , comparable to what is assumed by Buttery et al. (Reference Buttery, Park, McClenaghan, Weisberg, Canik, Ferron, Garofalo, Holcomb, Leuer and Snyder2021), which yields the functional relation
, comparable to what is assumed by Buttery et al. (Reference Buttery, Park, McClenaghan, Weisberg, Canik, Ferron, Garofalo, Holcomb, Leuer and Snyder2021), which yields the functional relation
Figure 23 shows plots of (A3) for different values of $Q_{{\rm fusion}}$![]() . The slight offset and kink in the curves at low values of $P_{{\rm net}}$
. The slight offset and kink in the curves at low values of $P_{{\rm net}}$![]() comes from imposing a minimum $P_{{\rm BOP}}$
comes from imposing a minimum $P_{{\rm BOP}}$![]() of 25 MW, but as can be seen, this assumption does not impact the conclusions meaningfully.
of 25 MW, but as can be seen, this assumption does not impact the conclusions meaningfully.

Figure 23. Net electric power predicted by (A3) as a function of $Q_{{\rm fusion}}$![]() and $P_{{\rm aux}}$
and $P_{{\rm aux}}$![]() .
.