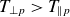1. Introduction
In situ observations pervasively indicate the occurrence of non-thermal features, e.g. temperature anisotropy and suprathermal particles in the solar wind and Earth’s magnetospheric plasma environments. Such non-thermal characteristics of the initial distribution lead to turbulent enhancements of various waves and instabilities. These enhanced turbulences of electromagnetic fields cover a wide range of lengths and time scales in different dilute space plasmas, e.g. planetary magnetospheric regions. The particles located away from their equilibrium positions get scattered with such amplified fluctuations and relocate themselves in relatively less energetic equilibrium states. Double adiabatic fluid theory seems inadequate to explain such relaxed/bounded states of charge particles observed in various space plasmas (Chew et al. Reference Chew, Goldberger and Low1956). One of the key models appearing to explain such discrepancies between theory and observations is the kinetic formalism on the basis of the linearised Vlasov–Maxwell equations. Extensive studies have successfully established the role of microinstabilities in defining the instability thresholds and states of the particles. For the choice of thermal, geometrical and polarisation limits, various instabilities are quantified using the linearised solution of the Vlasov–Maxwell equations, particle-in-cell simulations and hybrid simulations in the linear and quasilinear regimes of instability evolution/excitation (Feldman et al. Reference Feldman, Asbridge, Bame, Montgomery and Gary1975; Gary et al. Reference Gary, Feldman, Forslund and Montgomery1975; Gary & Feldman Reference Gary and Feldman1977; Gary et al. Reference Gary, Moldwin, Thomsen, Winske and Mccomas1994; Seough & Yoon Reference Seough and Yoon2012; Sarfraz Reference Sarfraz2018; Bilal et al. Reference Bilal, ur Rehman, Ahmad, Shahzad, Sarfraz and Mahmood2023).
The realistic estimations/predictions of various instabilities are the direct consequences of the actual distribution function. Based on the energy and density, electrons are observed in their decomposed forms. Core electrons with relatively high population and low energies are best fitted with the usual standard bi-Maxwellian form. On the other hand, tenuous and energetic halo electrons with extended tails require a power-law distribution, e.g. kappa distribution, for their actual representations (Maksimovic et al. Reference Maksimovic2005; Stverak et al. Reference Stverak, Travnicek, Maksimovic, Marsch, Fazakerley and Scime2008). In fast solar wind conditions, field-aligned strahl electrons are usually fitted with a drifting bi-Maxwellian velocity distribution. Focusing on the Earth’s magnetospheric space regions, protons are also observed with two distinguishable components based on their density and thermal velocities (Gary et al. Reference Gary, Moldwin, Thomsen, Winske and Mccomas1994). Recent observations of the Magnetospheric Multi-scale Mission (MMS) further validate the presence of cold and hot protons with their distinct features (Toledo et al. Reference Toledo-Redondo2021; Liu et al. Reference Liu2024).
Electromagnetic ion cyclotron (EMIC) or proton cyclotron (PC) instability is identified as one of the mechanisms to generate a variety of waves in the solar wind and magnetospheric regions. Amplified fluctuations of nearly PC frequency appear due to PC instability which significantly scatters the energetic protons. In the non-collisional state of space plasmas, PC instability is a major candidate to redefine the perpendicular temperature to gain lower (nearly isotropic) stable states. Proton cyclotron instability has a left-handed polarisation and appears in the large proton perpendicular temperature condition, i.e.
![]() $T_{\perp p}\gt T_{\parallel p}$
(Gary & Winske Reference Gary and Winske1990; Gary Reference Gary1992). Real oscillatory and imaginary frequency of the proton/ion cyclotron mode is sensitive to the particle and medium structures (Harris Reference Harris1961; Sagdeev Reference Sagdeev and Shafranov1961). Previously, notable revisions in the instability threshold conditions were investigated in the presence of different ion compositions, nonlinear effects and field-aligned drifts of different magnitudes (Maruca Reference Maruca, Kasper and Gary2012; Matteini Reference Matteini, Hellinger, Landi, Trávníček and Velli2012; Isenberg Reference Isenberg, Maruca and Kasper2013). In the solar wind conditions, Shaaban et al. (Reference Shaaban, Lazar, Poedts and Elhanbaly2016) revealed the impact of the interplay between anisotropic core–halo protons and non-thermal parameter of halo protons on the dispersion properties and resulting threshold conditions of EMIC instability. In the empirical relation
$T_{\perp p}\gt T_{\parallel p}$
(Gary & Winske Reference Gary and Winske1990; Gary Reference Gary1992). Real oscillatory and imaginary frequency of the proton/ion cyclotron mode is sensitive to the particle and medium structures (Harris Reference Harris1961; Sagdeev Reference Sagdeev and Shafranov1961). Previously, notable revisions in the instability threshold conditions were investigated in the presence of different ion compositions, nonlinear effects and field-aligned drifts of different magnitudes (Maruca Reference Maruca, Kasper and Gary2012; Matteini Reference Matteini, Hellinger, Landi, Trávníček and Velli2012; Isenberg Reference Isenberg, Maruca and Kasper2013). In the solar wind conditions, Shaaban et al. (Reference Shaaban, Lazar, Poedts and Elhanbaly2016) revealed the impact of the interplay between anisotropic core–halo protons and non-thermal parameter of halo protons on the dispersion properties and resulting threshold conditions of EMIC instability. In the empirical relation
![]() $T_{\perp i}/T_{\parallel i}=1+S\beta _{\parallel i}^{-\alpha }$
of the marginal stability condition of EMIC (or PC) instability, the dimensionless parameters
$T_{\perp i}/T_{\parallel i}=1+S\beta _{\parallel i}^{-\alpha }$
of the marginal stability condition of EMIC (or PC) instability, the dimensionless parameters
![]() $(S,\alpha )$
have been reported in a hybrid simulation (Gary et al. Reference Gary, Moldwin, Thomsen, Winske and Mccomas1994), observation fitting method (Anderson Reference Anderson, Denton, Ho, Hamilton, Fuselier and Strangeway1996) and with the solution of the linearised Vlasov equation (Gary et al. Reference Gary, Moldwin, Thomsen, Winske and Mccomas1994). From the observational perspective, Gary et al. (Reference Gary, Moldwin, Thomsen, Winske and Mccomas1994) and Toledo et al. (Reference Toledo-Redondo2021) reported the presence of multi-proton components in the Earth’s magnetosphere. Based on these notable achievements, the dispersion characteristics of strictly parallel PC (Gary et al. Reference Gary, Moldwin, Thomsen, Winske and Mccomas1994) and oblique EMIC (Toledo et al. Reference Toledo-Redondo2021) are studied for the conditions typical of magnetospheric regions.
$(S,\alpha )$
have been reported in a hybrid simulation (Gary et al. Reference Gary, Moldwin, Thomsen, Winske and Mccomas1994), observation fitting method (Anderson Reference Anderson, Denton, Ho, Hamilton, Fuselier and Strangeway1996) and with the solution of the linearised Vlasov equation (Gary et al. Reference Gary, Moldwin, Thomsen, Winske and Mccomas1994). From the observational perspective, Gary et al. (Reference Gary, Moldwin, Thomsen, Winske and Mccomas1994) and Toledo et al. (Reference Toledo-Redondo2021) reported the presence of multi-proton components in the Earth’s magnetosphere. Based on these notable achievements, the dispersion characteristics of strictly parallel PC (Gary et al. Reference Gary, Moldwin, Thomsen, Winske and Mccomas1994) and oblique EMIC (Toledo et al. Reference Toledo-Redondo2021) are studied for the conditions typical of magnetospheric regions.
In the recent past, quasilinear analysis appeared as a robust mathematical tool to study and re-examine wave dynamics in more detail. Based on such a simplified nonlinear or reduced quasilinear approach, we can trace the back actions of various unstable modes on the particle distributions. Such comprehensive and more physics-based techniques are quite helpful to display the time variation in physical quantities which otherwise are observed in experimental (Vinas et al. Reference Vinas, Gurgiolo, Nieves-Chinchilla, Garry and Golsteina2010) or simulation (Hellinger Reference Hellinger, Trávníček, Decyk and Schriver2014; Sarfraz et al. Reference Sarfraz, López, Ahmed and Yoon2022) studies. Guided by observational magnetospheric data (Gary et al. Reference Gary, Moldwin, Thomsen, Winske and Mccomas1994; Toledo et al. Reference Toledo-Redondo2021; Liu et al. Reference Liu2024), we take cold protons as thermally isotropic and adopt anisotropic hot protons as being distributed in a bi-Maxwellian manner. For our choice of different initial outer magnetospheric conditions, we will solve exactly numerically the set of instantaneous dispersion relation, dynamical temperature equations and wave-energy density equation. We will make use of a FORTRAN compiler to build and execute our required files and plot them in Matlab. The quasilinear evolution technique for the proton/ion cyclotron instability was applied in the case of single bi-Maxwellian-distributed ions (Seough & Yoon Reference Seough and Yoon2012) and the results were also validated/confirmed in simulations (Seough et al. Reference Seough, Yoon and cHwang2014). Later on, Shaaban et al. (Reference Shaaban, Lazar and Schlickeiser2021) extended these findings for non-thermal kappa-distributed ions in solar wind conditions. To our best knowledge, there has not yet been an investigation of the isotropic cold and anisotropic hot proton components in magnetospheric conditions. For the case of electrons, Sarfraz et al. (Reference Sarfraz, Saeed, Yoon, Abbas and Shah2016) have successfully demonstrated the time variations/saturations in the core and halo distributions and the resulting wave intensity. With the help of the quasilinear evolution technique, they were also able to define the marginal stability curves in phase space which otherwise are deduced through simulation or observational fitting method (Lazar et al. Reference Lazar, Poedts, Schlickeiser and Dumitrache2015). Some important quasilinear studies for ions (Yoon & Seough Reference Yoon and Seough2012; Yoon et al. Reference Yoon, Seough, Kim and Lee2012; Seough et al. Reference Seough, Yoon, Kim and Lee2013), electrons (Sarfraz et al. Reference Sarfraz, Saeed, Yoon, Abbas and Shah2017; Sarfraz Reference Sarfraz2018) and the combination there of (Shaaban et al. Reference Shaaban, Lazar, Yoon and Poedts2019; Sarfraz & Yoon Reference Sarfraz and Yoon2019) and validation against simulations (Seough et al. Reference Seough, Yoon and cHwang2014; Kim Reference Kim, Hwang, Seough and Yoon2017) motivate us to adopt this technique to report the dynamics of PC instability in the Earth’s magnetospheric region.
The plan of this paper is as follows. Section 2 describes the mathematical background and the model distribution for the quasilinear evolution of PC instability. Section 3 presents the numerical solutions of self-consistent quasilinear kinetic equations for the different input set-up formed with anisotropic hot protons and their relative density. The conclusion is presented in § 4.
2. Mathematical background
We assume a homogeneous, poorly collisional and non-relativistic magnetospheric electron–proton plasma. Protons are further decomposed into their cold and hot components (Gary et al. Reference Gary, Moldwin, Thomsen, Winske and Mccomas1994; Toledo et al. Reference Toledo-Redondo2021; Liu et al. Reference Liu2024). In the aforementioned conditions, the PC frequency,
![]() $\omega$
, and wave vector,
$\omega$
, and wave vector,
![]() $k$
(propagating strictly along the ambient magnetic field), satisfy the following instantaneous dispersion relation (Gary Reference Gary1993; Schlickeiser Reference Schlickeiser2002):
$k$
(propagating strictly along the ambient magnetic field), satisfy the following instantaneous dispersion relation (Gary Reference Gary1993; Schlickeiser Reference Schlickeiser2002):
 \begin{eqnarray} \frac {c^2k^2}{\omega ^2} &\,=\,& 1+\sum _{\sigma =e,c,h} \frac {\omega _{p\sigma }^2}{\omega ^2}\int \textrm{d}\boldsymbol{v} \,\frac {v_\perp /2}{\omega -kv_\parallel \pm \varOmega _\sigma } \nonumber \\ && \times \left ((\omega -kv_\parallel )\frac {\partial f_\sigma } {\partial v_\perp }+kv_\perp \frac {\partial f_\sigma } {\partial v_\parallel }\right ), \end{eqnarray}
\begin{eqnarray} \frac {c^2k^2}{\omega ^2} &\,=\,& 1+\sum _{\sigma =e,c,h} \frac {\omega _{p\sigma }^2}{\omega ^2}\int \textrm{d}\boldsymbol{v} \,\frac {v_\perp /2}{\omega -kv_\parallel \pm \varOmega _\sigma } \nonumber \\ && \times \left ((\omega -kv_\parallel )\frac {\partial f_\sigma } {\partial v_\perp }+kv_\perp \frac {\partial f_\sigma } {\partial v_\parallel }\right ), \end{eqnarray}
where
![]() $\sigma =e,c,h$
represents electrons and cold/hot proton components. We use ‘
$\sigma =e,c,h$
represents electrons and cold/hot proton components. We use ‘
![]() $+$
’ and ‘
$+$
’ and ‘
![]() $-$
’ to differentiate between right- and left-hand polarisations, respectively;
$-$
’ to differentiate between right- and left-hand polarisations, respectively;
![]() $\omega _{p\sigma }=(4\pi n_0e^2/m_\sigma )^{1/2}$
represents the plasma frequency;
$\omega _{p\sigma }=(4\pi n_0e^2/m_\sigma )^{1/2}$
represents the plasma frequency;
![]() $e$
,
$e$
,
![]() $c$
,
$c$
,
![]() $n_0$
and
$n_0$
and
![]() $m_{\sigma }$
designate the unit electric charge, speed of light in vacuum, total number density and mass of protons species labelled
$m_{\sigma }$
designate the unit electric charge, speed of light in vacuum, total number density and mass of protons species labelled
![]() $\sigma$
, respectively;
$\sigma$
, respectively;
![]() $\varOmega _\sigma =eB_0/m_\sigma c$
is the PC frequency, where
$\varOmega _\sigma =eB_0/m_\sigma c$
is the PC frequency, where
![]() $B_0$
represents the intensity of the ambient magnetic field.
$B_0$
represents the intensity of the ambient magnetic field.
To re-examine the wave dynamics in more detail and possible back action of the PC instability on the initial cold and hot proton distributions, we will make use of reduced macroscopic quasilinear theory. A moment-based quasilinear theory makes use of the following particle kinetic equation under the diffusion approximation:
 \begin{eqnarray} \frac {\partial f_\sigma }{\partial t} &\,=\,& \frac {ie^2}{4m_\sigma ^2c^2}\frac {1}{v_\perp } \int _{-\infty }^\infty \frac {\textrm{d}k}{k^2}\left [\left ( \omega ^*-kv_\parallel \right )\frac {\partial } {\partial v_\perp }+kv_\perp \frac {\partial } {\partial v_\parallel }\right ] \nonumber \\ && \times \frac {v_\perp \delta B^2(k,\omega )} {\omega -kv_\parallel \pm \varOmega _\sigma } \left [\left (\omega -kv_\parallel \right ) \frac {\partial f_\sigma }{\partial v_\perp }+kv_\perp \frac {\partial f_\sigma }{\partial v_\parallel }\right ], \end{eqnarray}
\begin{eqnarray} \frac {\partial f_\sigma }{\partial t} &\,=\,& \frac {ie^2}{4m_\sigma ^2c^2}\frac {1}{v_\perp } \int _{-\infty }^\infty \frac {\textrm{d}k}{k^2}\left [\left ( \omega ^*-kv_\parallel \right )\frac {\partial } {\partial v_\perp }+kv_\perp \frac {\partial } {\partial v_\parallel }\right ] \nonumber \\ && \times \frac {v_\perp \delta B^2(k,\omega )} {\omega -kv_\parallel \pm \varOmega _\sigma } \left [\left (\omega -kv_\parallel \right ) \frac {\partial f_\sigma }{\partial v_\perp }+kv_\perp \frac {\partial f_\sigma }{\partial v_\parallel }\right ], \end{eqnarray}
where
![]() $\omega =\omega _k+{\rm i}\gamma _k$
represents the complex root of (2.1). Results of (2.1) in the form of real oscillatory frequency
$\omega =\omega _k+{\rm i}\gamma _k$
represents the complex root of (2.1). Results of (2.1) in the form of real oscillatory frequency
![]() $\omega _r$
and growth rate
$\omega _r$
and growth rate
![]() $\gamma _k$
will affect the nonlinear evolution of PC instability. Here,
$\gamma _k$
will affect the nonlinear evolution of PC instability. Here,
![]() $\delta B^2(k)$
is the spectral wave energy density associated with PC magnetic field perturbations.
$\delta B^2(k)$
is the spectral wave energy density associated with PC magnetic field perturbations.
2.1. Model distribution function
In situ measurements recorded during various space missions located in magnetospheric regions guide us to take the protons in their constituent components. We adopt the following bi-Maxwellian form of the velocity distribution:
 \begin{equation} f_\sigma =\frac {1}{\pi ^{3/2}\alpha _{\perp \sigma }^2(t) \alpha _{\parallel \sigma }(t)}\exp \left ( -\frac {v_\perp ^2}{\alpha _{\perp \sigma }^2(t)} -\frac {v_\parallel ^2}{\alpha _{\parallel \sigma }^2(t)}\right ) \end{equation}
\begin{equation} f_\sigma =\frac {1}{\pi ^{3/2}\alpha _{\perp \sigma }^2(t) \alpha _{\parallel \sigma }(t)}\exp \left ( -\frac {v_\perp ^2}{\alpha _{\perp \sigma }^2(t)} -\frac {v_\parallel ^2}{\alpha _{\parallel \sigma }^2(t)}\right ) \end{equation}
all the time, except that we allow the perpendicular and parallel temperatures to vary in time
![]() $t$
. Here
$t$
. Here
![]() $\sigma =e,c,h$
stands for electrons and cold/hot protons. For the linear stability analysis of the PC mode, we will adopt cold protons as thermally isotropic and hot protons as anisotropic. As the instability will enter the nonlinear phase, the time variations in the cold/hot proton temperatures will be helpful to examine the loss or gain in the initial anisotropy values. In (2.3),
$\sigma =e,c,h$
stands for electrons and cold/hot protons. For the linear stability analysis of the PC mode, we will adopt cold protons as thermally isotropic and hot protons as anisotropic. As the instability will enter the nonlinear phase, the time variations in the cold/hot proton temperatures will be helpful to examine the loss or gain in the initial anisotropy values. In (2.3),
![]() $\alpha _{\perp \sigma }$
and
$\alpha _{\perp \sigma }$
and
![]() $\alpha _{\parallel \sigma }$
stand for perpendicular and parallel thermal speeds for each species labelled
$\alpha _{\parallel \sigma }$
stand for perpendicular and parallel thermal speeds for each species labelled
![]() $\sigma$
, which are defined by
$\sigma$
, which are defined by
 \begin{eqnarray} T_{\perp \sigma } &\,=\,& \frac {m_\sigma }{2}\int \textrm{d}\boldsymbol{v}v_\perp ^2f_\sigma =\frac {m_\sigma \alpha _{\perp \sigma }^2}{2}, \nonumber \\ T_{\parallel \sigma } &\,=\,& m_\sigma \int \textrm{d}\boldsymbol{v}v_\parallel ^2f_\sigma =\frac {m_\sigma \alpha _{\parallel \sigma }^2}{2}, \end{eqnarray}
\begin{eqnarray} T_{\perp \sigma } &\,=\,& \frac {m_\sigma }{2}\int \textrm{d}\boldsymbol{v}v_\perp ^2f_\sigma =\frac {m_\sigma \alpha _{\perp \sigma }^2}{2}, \nonumber \\ T_{\parallel \sigma } &\,=\,& m_\sigma \int \textrm{d}\boldsymbol{v}v_\parallel ^2f_\sigma =\frac {m_\sigma \alpha _{\parallel \sigma }^2}{2}, \end{eqnarray}
and
![]() $m_\sigma$
is the mass of charged species labelled
$m_\sigma$
is the mass of charged species labelled
![]() $\sigma$
. The perpendicular and parallel velocity vector components are defined by
$\sigma$
. The perpendicular and parallel velocity vector components are defined by
![]() $v_\perp$
and
$v_\perp$
and
![]() $v_\parallel$
in cylindrical coordinates. We have omitted the Boltzmann constant, such that the thermal energy is in c.g.s. energy units.
$v_\parallel$
in cylindrical coordinates. We have omitted the Boltzmann constant, such that the thermal energy is in c.g.s. energy units.
Our approximation of allowing the time variation in thermal velocities,
![]() $\alpha _{\perp \sigma }(t)$
and
$\alpha _{\perp \sigma }(t)$
and
![]() $\alpha _{\perp \sigma }(t)$
, may lead to a notable distortion in the distribution (Hellinger Reference Hellinger, Trávníček, Decyk and Schriver2014) in response to the excitation of PC instability in the nonlinear phase. From the various simulation studies conducted to see the evolution of the distribution function (Seough et al. Reference Seough, Yoon and cHwang2014; Kim Reference Kim, Hwang, Seough and Yoon2017), it is noted that any change in the initial distribution will only be in the transit states. In the later time of the instability evolution, particles with initial high perpendicular velocities start to diffuse along the pitch angle paths. A nearly isotropic form of the distribution is recovered at the end of the simulation run, which largely validates our assumption regarding the form of the velocity distribution. Such an assumption has been successfully tested in various comparative quasilinear versus simulation studies (Seough et al. Reference Seough, Yoon and cHwang2014, Reference Seough, Yoon, Hwang and Nariyuki2015; Yoon et al. Reference Yoon, Seough, Hwang and Nariyuki2015, Reference Yoon, López, Seough and Sarfraz2017; Sarfraz et al. Reference Sarfraz, López, Ahmed and Yoon2022) and displayed more than good agreement between results. These better comparative findings for the different instabilities motivate us to adopt this approximation and allow us to re-examine the wave dynamics more carefully and in detail.
$\alpha _{\perp \sigma }(t)$
, may lead to a notable distortion in the distribution (Hellinger Reference Hellinger, Trávníček, Decyk and Schriver2014) in response to the excitation of PC instability in the nonlinear phase. From the various simulation studies conducted to see the evolution of the distribution function (Seough et al. Reference Seough, Yoon and cHwang2014; Kim Reference Kim, Hwang, Seough and Yoon2017), it is noted that any change in the initial distribution will only be in the transit states. In the later time of the instability evolution, particles with initial high perpendicular velocities start to diffuse along the pitch angle paths. A nearly isotropic form of the distribution is recovered at the end of the simulation run, which largely validates our assumption regarding the form of the velocity distribution. Such an assumption has been successfully tested in various comparative quasilinear versus simulation studies (Seough et al. Reference Seough, Yoon and cHwang2014, Reference Seough, Yoon, Hwang and Nariyuki2015; Yoon et al. Reference Yoon, Seough, Hwang and Nariyuki2015, Reference Yoon, López, Seough and Sarfraz2017; Sarfraz et al. Reference Sarfraz, López, Ahmed and Yoon2022) and displayed more than good agreement between results. These better comparative findings for the different instabilities motivate us to adopt this approximation and allow us to re-examine the wave dynamics more carefully and in detail.
Under the application of our model function distribution given in (2.3), the complex frequency and wavenumber satisfy the following equation:
 \begin{eqnarray} 0 &\,=\,& \frac {c^2k^2}{\omega ^2}- \nonumber \\[6pt] && \sum _{\sigma =e,c,h}\frac {\omega _{p\sigma }^2} {\omega ^2}\biggl \{\frac {T_{\perp \sigma }}{T_{\parallel \sigma }}-1 +\biggl [\frac {T_{\perp \sigma }}{T_{\parallel \sigma }}\,\omega \pm \biggl (\frac {T_{\perp \sigma }}{T_{\parallel \sigma }}-1\biggr ) \varOmega _\sigma \biggr ]\frac {1}{k\alpha _{\parallel \sigma }}\,Z\biggl ( \frac {\omega \pm \varOmega _\sigma }{k\alpha _{\parallel \sigma }}\biggr )\biggr \}.\quad \end{eqnarray}
\begin{eqnarray} 0 &\,=\,& \frac {c^2k^2}{\omega ^2}- \nonumber \\[6pt] && \sum _{\sigma =e,c,h}\frac {\omega _{p\sigma }^2} {\omega ^2}\biggl \{\frac {T_{\perp \sigma }}{T_{\parallel \sigma }}-1 +\biggl [\frac {T_{\perp \sigma }}{T_{\parallel \sigma }}\,\omega \pm \biggl (\frac {T_{\perp \sigma }}{T_{\parallel \sigma }}-1\biggr ) \varOmega _\sigma \biggr ]\frac {1}{k\alpha _{\parallel \sigma }}\,Z\biggl ( \frac {\omega \pm \varOmega _\sigma }{k\alpha _{\parallel \sigma }}\biggr )\biggr \}.\quad \end{eqnarray}
In (2.5) the plasma dispersion function is defined by
![]() $Z(\zeta ) =\int _{-\infty }^\infty (x-\zeta )^{-1}e^{-x^2}\,\textrm{d}x$
. In the mathematical procedure to reach the instantaneous dispersion relation (2.5), we have ignored the displacement current, as we are not interested in fast waves, i.e. we assume
$Z(\zeta ) =\int _{-\infty }^\infty (x-\zeta )^{-1}e^{-x^2}\,\textrm{d}x$
. In the mathematical procedure to reach the instantaneous dispersion relation (2.5), we have ignored the displacement current, as we are not interested in fast waves, i.e. we assume
![]() $ck/\omega \gg 1$
here. For the left-hand circularly polarised mode, we may take electrons as isotropic (
$ck/\omega \gg 1$
here. For the left-hand circularly polarised mode, we may take electrons as isotropic (
![]() $T_{\perp e}=T_{\parallel e}=T_e$
) and ignore their thermal effects, i.e
$T_{\perp e}=T_{\parallel e}=T_e$
) and ignore their thermal effects, i.e
![]() ${\omega \mp |\varOmega _e|}/{k\alpha _{\parallel e}}\gg 1$
. We approximate
${\omega \mp |\varOmega _e|}/{k\alpha _{\parallel e}}\gg 1$
. We approximate
![]() $\omega -\varOmega _e\approx |\varOmega _e|$
and make use of
$\omega -\varOmega _e\approx |\varOmega _e|$
and make use of
![]() ${\omega ^2_{pe}}/{\omega ^2(\mp |\varOmega _e|)}={\omega ^2_{pp}}/{\omega ^2(\mp \varOmega _p)}$
to get the final dispersion relation of the PC mode as
${\omega ^2_{pe}}/{\omega ^2(\mp |\varOmega _e|)}={\omega ^2_{pp}}/{\omega ^2(\mp \varOmega _p)}$
to get the final dispersion relation of the PC mode as
 \begin{eqnarray} 0 &\,=\,& \frac {c^2k^2}{\omega _p^2}+\frac {\omega }{\varOmega _p} \nonumber \\[6pt] && -\frac {n_c}{n_0}\left \{ \frac {T_{\perp c}}{T_{\parallel c}}-1 +\left [\frac {T_{\perp c}}{T_{\parallel c}}\,\omega -\left (\frac {T_{\perp c}}{T_{\parallel c}}-1\right ) \varOmega _p\right ]\frac {1}{k\alpha _{\parallel c}}\,Z\left ( \frac {\omega -\varOmega _p}{k\alpha _{\parallel c}}\right )\right \} \nonumber \\[6pt] && -\frac {n_h}{n_0}\left \{ \frac {T_{\perp h}}{T_{\parallel h}}-1 +\left [\frac {T_{\perp h}}{T_{\parallel h}}\,\omega -\left (\frac {T_{\perp h}}{T_{\parallel h}}-1\right ) \varOmega _e\right ]\frac {1}{k\alpha _{\parallel h}}\,Z\left ( \frac {\omega -\varOmega _p}{k\alpha _{\parallel h}}\right )\right \}. \end{eqnarray}
\begin{eqnarray} 0 &\,=\,& \frac {c^2k^2}{\omega _p^2}+\frac {\omega }{\varOmega _p} \nonumber \\[6pt] && -\frac {n_c}{n_0}\left \{ \frac {T_{\perp c}}{T_{\parallel c}}-1 +\left [\frac {T_{\perp c}}{T_{\parallel c}}\,\omega -\left (\frac {T_{\perp c}}{T_{\parallel c}}-1\right ) \varOmega _p\right ]\frac {1}{k\alpha _{\parallel c}}\,Z\left ( \frac {\omega -\varOmega _p}{k\alpha _{\parallel c}}\right )\right \} \nonumber \\[6pt] && -\frac {n_h}{n_0}\left \{ \frac {T_{\perp h}}{T_{\parallel h}}-1 +\left [\frac {T_{\perp h}}{T_{\parallel h}}\,\omega -\left (\frac {T_{\perp h}}{T_{\parallel h}}-1\right ) \varOmega _e\right ]\frac {1}{k\alpha _{\parallel h}}\,Z\left ( \frac {\omega -\varOmega _p}{k\alpha _{\parallel h}}\right )\right \}. \end{eqnarray}
Taking the velocity moments for the model distribution function (2.3), the particle kinetic equation (2.2) for the left-hand-polarised mode can be rewritten in the form of dynamic temperatures as
 \begin{eqnarray} \frac {\textrm{d}T_{\perp c}}{\textrm{d}t} &\,=\,& -\frac {e^2}{2m_pc^2} \int _{-\infty }^\infty \frac {\textrm{d}k}{k^2}\,\delta B^2(k) \left \{\left (\frac {2T_{\perp c}}{T_{\parallel c}} -1\right )\gamma _k\right . \nonumber \\[3pt] && +\textrm { Im}\,\frac {2i\gamma _k-\varOmega _p} {k\alpha _{\parallel c}}\left [\frac {T_{\perp c}} {T_{\parallel c}}\,\omega -\left ( \frac {T_{\perp c}}{T_{\parallel c}}-1\right ) \varOmega _p\right ] \nonumber \\[3pt] && \left .\times Z\left (\frac {\omega -\varOmega _p} {k\alpha _{\parallel c}}\right )\right \}, \nonumber \\[3pt] \frac {\textrm{d}T_{\parallel c}}{\textrm{d}t} &\,=\,& \frac {e^2}{m_pc^2} \int _{-\infty }^\infty \frac {\textrm{d}k}{k^2}\,\delta B^2(k) \left \{\frac {T_{\perp c}}{T_{\parallel c}}\,\gamma _k\right . \nonumber \\[3pt] && +\textrm { Im}\,\frac {\omega -\varOmega _p}{k\alpha _{\parallel \sigma }} \left [\frac {T_{\perp c}}{T_{\parallel c}} \,\omega -\left (\frac {T_{\perp c}}{T_{\parallel c}} -1\right )\varOmega _p\right ] \nonumber \\[3pt] && \left .\times \,Z\left (\frac {\omega -\varOmega _p} {k\alpha _{\parallel c}}\right )\right \}, \nonumber \\[3pt] \frac {\textrm{d}T_{\perp h}}{\textrm{d}t} &\,=\,& -\frac {e^2}{2m_pc^2} \int _{-\infty }^\infty \frac {\textrm{d}k}{k^2}\,\delta B^2(k) \left \{\left (\frac {2T_{\perp h}}{T_{\parallel h}} -1\right )\gamma _k\right . \nonumber \\[3pt] && +\textrm { Im}\,\frac {2i\gamma _k-\varOmega _p} {k\alpha _{\parallel h}}\left [\frac {T_{\perp h}} {T_{\parallel h}}\,\omega -\left ( \frac {T_{\perp h}}{T_{\parallel h}}-1\right ) \varOmega _p\right ] \nonumber \\[3pt] && \left .\times Z\left (\frac {\omega -\varOmega _p} {k\alpha _{\parallel h}}\right )\right \}, \nonumber \\ \frac {\textrm{d}T_{\parallel h}}{\textrm{d}t} &\,=\,& \frac {e^2}{m_pc^2} \int _{-\infty }^\infty \frac {\textrm{d}k}{k^2}\,\delta B^2(k) \left \{\frac {T_{\perp h}}{T_{\parallel h}}\,\gamma _k\right . \nonumber \\ && +\textrm { Im}\,\frac {\omega -\varOmega _p}{k\alpha _{\parallel h}} \left [\frac {T_{\perp h}}{T_{\parallel h}} \,\omega -\left (\frac {T_{\perp h}}{T_{\parallel h}} -1\right )\varOmega _p\right ] \nonumber \\ && \left .\times \,Z\left (\frac {\omega -\varOmega _p} {k\alpha _{\parallel h}}\right )\right \}. \end{eqnarray}
\begin{eqnarray} \frac {\textrm{d}T_{\perp c}}{\textrm{d}t} &\,=\,& -\frac {e^2}{2m_pc^2} \int _{-\infty }^\infty \frac {\textrm{d}k}{k^2}\,\delta B^2(k) \left \{\left (\frac {2T_{\perp c}}{T_{\parallel c}} -1\right )\gamma _k\right . \nonumber \\[3pt] && +\textrm { Im}\,\frac {2i\gamma _k-\varOmega _p} {k\alpha _{\parallel c}}\left [\frac {T_{\perp c}} {T_{\parallel c}}\,\omega -\left ( \frac {T_{\perp c}}{T_{\parallel c}}-1\right ) \varOmega _p\right ] \nonumber \\[3pt] && \left .\times Z\left (\frac {\omega -\varOmega _p} {k\alpha _{\parallel c}}\right )\right \}, \nonumber \\[3pt] \frac {\textrm{d}T_{\parallel c}}{\textrm{d}t} &\,=\,& \frac {e^2}{m_pc^2} \int _{-\infty }^\infty \frac {\textrm{d}k}{k^2}\,\delta B^2(k) \left \{\frac {T_{\perp c}}{T_{\parallel c}}\,\gamma _k\right . \nonumber \\[3pt] && +\textrm { Im}\,\frac {\omega -\varOmega _p}{k\alpha _{\parallel \sigma }} \left [\frac {T_{\perp c}}{T_{\parallel c}} \,\omega -\left (\frac {T_{\perp c}}{T_{\parallel c}} -1\right )\varOmega _p\right ] \nonumber \\[3pt] && \left .\times \,Z\left (\frac {\omega -\varOmega _p} {k\alpha _{\parallel c}}\right )\right \}, \nonumber \\[3pt] \frac {\textrm{d}T_{\perp h}}{\textrm{d}t} &\,=\,& -\frac {e^2}{2m_pc^2} \int _{-\infty }^\infty \frac {\textrm{d}k}{k^2}\,\delta B^2(k) \left \{\left (\frac {2T_{\perp h}}{T_{\parallel h}} -1\right )\gamma _k\right . \nonumber \\[3pt] && +\textrm { Im}\,\frac {2i\gamma _k-\varOmega _p} {k\alpha _{\parallel h}}\left [\frac {T_{\perp h}} {T_{\parallel h}}\,\omega -\left ( \frac {T_{\perp h}}{T_{\parallel h}}-1\right ) \varOmega _p\right ] \nonumber \\[3pt] && \left .\times Z\left (\frac {\omega -\varOmega _p} {k\alpha _{\parallel h}}\right )\right \}, \nonumber \\ \frac {\textrm{d}T_{\parallel h}}{\textrm{d}t} &\,=\,& \frac {e^2}{m_pc^2} \int _{-\infty }^\infty \frac {\textrm{d}k}{k^2}\,\delta B^2(k) \left \{\frac {T_{\perp h}}{T_{\parallel h}}\,\gamma _k\right . \nonumber \\ && +\textrm { Im}\,\frac {\omega -\varOmega _p}{k\alpha _{\parallel h}} \left [\frac {T_{\perp h}}{T_{\parallel h}} \,\omega -\left (\frac {T_{\perp h}}{T_{\parallel h}} -1\right )\varOmega _p\right ] \nonumber \\ && \left .\times \,Z\left (\frac {\omega -\varOmega _p} {k\alpha _{\parallel h}}\right )\right \}. \end{eqnarray}
The wave kinetic equation is given by
In deriving the set of self-consistent quasilinear kinetic (2.6), (2.7) and (2.8), we also assume a homogeneous plasma and wave propagation is strictly parallel (or antiparallel) to the ambient field. Introducing the obliqueness in the propagation will change the threshold conditions and may result in the excitation of the mirror instability (Yoon et al. Reference Yoon and Seough2012, Reference Yoon, Sarfraz, Ali, Salem and Seough2022) in the multi-component proton plasma. This is of course our future task and is beyond the scope of our present study.
3. Numerical analysis
To achieve the exact numerical analysis of (2.6), (2.7) and (2.8), we normalise them with following dimensionless quantities:
 \begin{eqnarray} \zeta _c &\,=\,& \frac {z-1}{q\beta _c^{1/2}},\qquad \zeta _h=\frac {z-1}{q\beta _h^{1/2}}, \nonumber \\ A_c &\,=\,& \frac {\beta _{\perp c}}{\beta _{\parallel c}}-1,\qquad A_h=\frac {\beta _{\perp h}}{\beta _{\parallel h}}-1, \nonumber \\ z &\,=\,& \frac {\omega }{\varOmega _p},\qquad q=\frac {ck}{\omega _{p}},\qquad \delta =\frac {n_h}{n_0}, \nonumber \\ \beta _c &\,=\,& \frac {8\pi n_cT_{\parallel c}}{B_0^2},\qquad \beta _h=\frac {8\pi n_hT_{\parallel h}}{B_0^2}, \nonumber \\ \eta _c &\,=\,& \frac {(A_c+1)z-A_c}{q\beta _{\parallel c}^{1/2}},\qquad \eta _h=\frac {(A_h+1)z-A_h}{q\beta _{\parallel h}^{1/2}}, \nonumber \\ \tau &\,=\,& \varOmega _pt,\qquad W(q)=\frac {\delta B^2(q)}{B_0^2}. \end{eqnarray}
\begin{eqnarray} \zeta _c &\,=\,& \frac {z-1}{q\beta _c^{1/2}},\qquad \zeta _h=\frac {z-1}{q\beta _h^{1/2}}, \nonumber \\ A_c &\,=\,& \frac {\beta _{\perp c}}{\beta _{\parallel c}}-1,\qquad A_h=\frac {\beta _{\perp h}}{\beta _{\parallel h}}-1, \nonumber \\ z &\,=\,& \frac {\omega }{\varOmega _p},\qquad q=\frac {ck}{\omega _{p}},\qquad \delta =\frac {n_h}{n_0}, \nonumber \\ \beta _c &\,=\,& \frac {8\pi n_cT_{\parallel c}}{B_0^2},\qquad \beta _h=\frac {8\pi n_hT_{\parallel h}}{B_0^2}, \nonumber \\ \eta _c &\,=\,& \frac {(A_c+1)z-A_c}{q\beta _{\parallel c}^{1/2}},\qquad \eta _h=\frac {(A_h+1)z-A_h}{q\beta _{\parallel h}^{1/2}}, \nonumber \\ \tau &\,=\,& \varOmega _pt,\qquad W(q)=\frac {\delta B^2(q)}{B_0^2}. \end{eqnarray}
Importantly, the plasma beta definitions of cold and hot protons,
![]() $\beta _{\parallel c}$
and
$\beta _{\parallel c}$
and
![]() $\beta _{\parallel h}$
, are consistent with those adopted by Lazar et al. (Reference Lazar, Yoon, López and Moya2018) and Yoon et al. (Reference Yoon, Salem, Klein, Martinović, López, Seough, Sarfraz, Lazar and Shaaban2024) for core–halo electron components. With these normalised quantities, the instantaneous dispersion relation (2.6), dynamical perpendicular and parallel temperatures of the constituent proton components (2.7) and the wave-energy density form (2.8) are rewritten as
$\beta _{\parallel h}$
, are consistent with those adopted by Lazar et al. (Reference Lazar, Yoon, López and Moya2018) and Yoon et al. (Reference Yoon, Salem, Klein, Martinović, López, Seough, Sarfraz, Lazar and Shaaban2024) for core–halo electron components. With these normalised quantities, the instantaneous dispersion relation (2.6), dynamical perpendicular and parallel temperatures of the constituent proton components (2.7) and the wave-energy density form (2.8) are rewritten as
 \begin{eqnarray} \frac {\textrm{d}\beta _{\perp c}}{\textrm{d}\tau } &\,=\,& -2\int _0^\infty \textrm{d}q\,\frac {W(q)}{q^2} \left [\left (2A_c+1\right )z_i\right . \nonumber \\ && \left .+\textrm { Im}\left (2iz_i-1\right ) \eta _cZ(\zeta _c)\right ], \nonumber \\ \frac {\textrm{d}\beta _{\parallel c}}{\textrm{d}\tau } &\,=\,& 4\int _0^\infty \textrm{d}q\,\frac {W(q)}{q^2} \left [\left (A_c+1\right )z_i\right . \nonumber \\ && \left .+\textrm { Im}\left (z-1\right )\eta _cZ(\zeta _c)\right ], \nonumber \\ \frac {\textrm{d}\beta _{\perp h}}{\textrm{d}\tau } &\,=\,& -2\int _0^\infty \textrm{d}q\,\frac {W(q)}{q^2} \left [\left (2A_h+1\right )z_i\right . \nonumber \\ && \left .+\textrm { Im}\left (2iz_i-1\right )\eta _hZ(\zeta _h)\right ], \nonumber \\ \frac {\textrm{d}\beta _{\parallel h}}{\textrm{d}\tau } &\,=\,& 4\int _0^\infty \textrm{d}q\,\frac {W(q)}{q^2} \left [\left (A_h+1\right )z_i\right . \nonumber \\ && \left .+\textrm {Im}\left (z-1\right )\eta _hZ(\zeta _h)\right ], \end{eqnarray}
\begin{eqnarray} \frac {\textrm{d}\beta _{\perp c}}{\textrm{d}\tau } &\,=\,& -2\int _0^\infty \textrm{d}q\,\frac {W(q)}{q^2} \left [\left (2A_c+1\right )z_i\right . \nonumber \\ && \left .+\textrm { Im}\left (2iz_i-1\right ) \eta _cZ(\zeta _c)\right ], \nonumber \\ \frac {\textrm{d}\beta _{\parallel c}}{\textrm{d}\tau } &\,=\,& 4\int _0^\infty \textrm{d}q\,\frac {W(q)}{q^2} \left [\left (A_c+1\right )z_i\right . \nonumber \\ && \left .+\textrm { Im}\left (z-1\right )\eta _cZ(\zeta _c)\right ], \nonumber \\ \frac {\textrm{d}\beta _{\perp h}}{\textrm{d}\tau } &\,=\,& -2\int _0^\infty \textrm{d}q\,\frac {W(q)}{q^2} \left [\left (2A_h+1\right )z_i\right . \nonumber \\ && \left .+\textrm { Im}\left (2iz_i-1\right )\eta _hZ(\zeta _h)\right ], \nonumber \\ \frac {\textrm{d}\beta _{\parallel h}}{\textrm{d}\tau } &\,=\,& 4\int _0^\infty \textrm{d}q\,\frac {W(q)}{q^2} \left [\left (A_h+1\right )z_i\right . \nonumber \\ && \left .+\textrm {Im}\left (z-1\right )\eta _hZ(\zeta _h)\right ], \end{eqnarray}
The above set of equations are now implicit functions of five input variables, i.e.
![]() $\delta$
,
$\delta$
,
![]() $\beta _c$
,
$\beta _c$
,
![]() $\beta _h$
,
$\beta _h$
,
![]() $A_c$
and
$A_c$
and
![]() $A_h$
. To solve them exactly numerically, we develop codes for the linear and quasilinear evolution of PC instability in Absoft Fortran to generate the required files based on different sets of initial conditions. We then formulate programs in Matlab to sketch graphically these executed files. Our choice of initial conditions to run the codes is typical of the magnetospheric conditions suggested in Gary et al. (Reference Gary, Moldwin, Thomsen, Winske and Mccomas1994), Toledo et al. (Reference Toledo-Redondo2021) and Liu et al. (Reference Liu2024). To start with, figure 1 is plotted with the following conditions:
$A_h$
. To solve them exactly numerically, we develop codes for the linear and quasilinear evolution of PC instability in Absoft Fortran to generate the required files based on different sets of initial conditions. We then formulate programs in Matlab to sketch graphically these executed files. Our choice of initial conditions to run the codes is typical of the magnetospheric conditions suggested in Gary et al. (Reference Gary, Moldwin, Thomsen, Winske and Mccomas1994), Toledo et al. (Reference Toledo-Redondo2021) and Liu et al. (Reference Liu2024). To start with, figure 1 is plotted with the following conditions:
 \begin{eqnarray} \frac {T_{\perp c}(0)}{T_{\parallel c}(0)} &\,=\,& \frac {\beta _{\perp c}(0)}{\beta _{\parallel c}(0)}= 1, \nonumber \\[5pt] \frac {T_{\perp h}(0)}{T_{\parallel h}(0)} &\,=\,& \frac {\beta _{\perp h}(0)}{\beta _{\parallel h}(0)} =7,\mbox{ }8,\mbox{ }9, \nonumber \\[5pt] \beta _{\parallel c} (0) &\,=\,& 1,\quad\beta _{\parallel h} (0) = 1,\quad \delta =0.07. \end{eqnarray}
\begin{eqnarray} \frac {T_{\perp c}(0)}{T_{\parallel c}(0)} &\,=\,& \frac {\beta _{\perp c}(0)}{\beta _{\parallel c}(0)}= 1, \nonumber \\[5pt] \frac {T_{\perp h}(0)}{T_{\parallel h}(0)} &\,=\,& \frac {\beta _{\perp h}(0)}{\beta _{\parallel h}(0)} =7,\mbox{ }8,\mbox{ }9, \nonumber \\[5pt] \beta _{\parallel c} (0) &\,=\,& 1,\quad\beta _{\parallel h} (0) = 1,\quad \delta =0.07. \end{eqnarray}

Figure 1. Effect of hot proton anisotropy on the dispersion properties of the PC mode: real oscillatory frequency,
![]() $\omega _r/\varOmega _p$
(top; solid), and growth rate,
$\omega _r/\varOmega _p$
(top; solid), and growth rate,
![]() $\gamma _k/\varOmega _{p}$
(bottom; dashed), versus normalised wavenumber,
$\gamma _k/\varOmega _{p}$
(bottom; dashed), versus normalised wavenumber,
![]() $ck/\omega _{p}$
, for different combinations of temperature ratio of hot protons.
$ck/\omega _{p}$
, for different combinations of temperature ratio of hot protons.
The details of these parameters are also provided in the figure title and within the plot. We display the impact of the anisotropic hot proton component on the real oscillatory wave frequency,
![]() $\omega _r$
, in the top panel and growth rate,
$\omega _r$
, in the top panel and growth rate,
![]() $\gamma _k$
, shown in the bottom panel against the propagation vector,
$\gamma _k$
, shown in the bottom panel against the propagation vector,
![]() $k$
. As given in (3.1), we normalise the real frequency with the PC frequency, i.e.
$k$
. As given in (3.1), we normalise the real frequency with the PC frequency, i.e.
![]() $\omega _r/\varOmega _p$
, and wave vector with proton skin depth, i.e.
$\omega _r/\varOmega _p$
, and wave vector with proton skin depth, i.e.
![]() $ck/\varOmega _p$
, and plot them on the x axis and y axis, respectively. We also differentiate the real and imaginary parts of the wave frequency with solid (upper) and dashed (lower) curves, respectively. Based on the average values of observed parameters given in Gary et al. (Reference Gary, Moldwin, Thomsen, Winske and Mccomas1994) and Toledo et al. (Reference Toledo-Redondo2021), we choose a range of hot proton perpendicular temperature anisotropy, i.e.
$ck/\varOmega _p$
, and plot them on the x axis and y axis, respectively. We also differentiate the real and imaginary parts of the wave frequency with solid (upper) and dashed (lower) curves, respectively. Based on the average values of observed parameters given in Gary et al. (Reference Gary, Moldwin, Thomsen, Winske and Mccomas1994) and Toledo et al. (Reference Toledo-Redondo2021), we choose a range of hot proton perpendicular temperature anisotropy, i.e.
![]() $T_{\perp h}/T_{\parallel h}=7{-}9$
, and keep the cold protons as thermally isotropic, i.e.
$T_{\perp h}/T_{\parallel h}=7{-}9$
, and keep the cold protons as thermally isotropic, i.e.
![]() $T_{\perp c}/T_{\parallel c}=1$
. Furthermore, we adopt the range of hot proton relative density,
$T_{\perp c}/T_{\parallel c}=1$
. Furthermore, we adopt the range of hot proton relative density,
![]() $\delta$
, using the geosynchronous orbit set (Gary et al. Reference Gary, Moldwin, Thomsen, Winske and Mccomas1994, Reference Gary, Thomsen, Yin and Winske1995; Toledo et al. Reference Toledo-Redondo2021) and EMIC mirror mode activities observed by MMS-1 (Toledo et al. Reference Toledo-Redondo2021; Liu et al. Reference Liu2024). Observations of these individual data set points correspond to the data (i) 11–20 November 1994 and (ii) 21–31 January 1994. We keep the initial relative hot proton density and plasma betas of both proton components as fixed. Shown in figure 1, initial higher perpendicular anisotropy supports the real oscillatory frequency of the PC mode (solid black curve). Similarly, the growth rate of PC instability keeps rising with the higher anisotropy ratio of the hot proton component (see the dashed black curve). A significant rise in the imaginary frequency (growth rate) of the PC wave validates the presence of more free energy associated with hot proton perpendicular temperature anisotropy.
$\delta$
, using the geosynchronous orbit set (Gary et al. Reference Gary, Moldwin, Thomsen, Winske and Mccomas1994, Reference Gary, Thomsen, Yin and Winske1995; Toledo et al. Reference Toledo-Redondo2021) and EMIC mirror mode activities observed by MMS-1 (Toledo et al. Reference Toledo-Redondo2021; Liu et al. Reference Liu2024). Observations of these individual data set points correspond to the data (i) 11–20 November 1994 and (ii) 21–31 January 1994. We keep the initial relative hot proton density and plasma betas of both proton components as fixed. Shown in figure 1, initial higher perpendicular anisotropy supports the real oscillatory frequency of the PC mode (solid black curve). Similarly, the growth rate of PC instability keeps rising with the higher anisotropy ratio of the hot proton component (see the dashed black curve). A significant rise in the imaginary frequency (growth rate) of the PC wave validates the presence of more free energy associated with hot proton perpendicular temperature anisotropy.
The impact of hot proton relative density in modifying/altering the dispersion characteristics of the PC mode is shown in figure 2. We make a choice of the following initial conditions:
 \begin{eqnarray} \delta &\,=\,& 0.05,\ 0.06,\ 0.07, \nonumber \\ \frac {T_{\perp c}(0)}{T_{\parallel c}(0)} &\,=\,& \frac {\beta _{\perp c}(0)}{\beta _{\parallel c}(0)}= 1, \nonumber \\ \frac {T_{\perp h}(0)}{T_{\parallel h}(0)} &\,=\,& \frac {\beta _{\perp h}(0)}{\beta _{\parallel h}(0)} =9, \nonumber \\ \beta _{\parallel c} (0) &\,=\,& 1,\quad \beta _{\parallel h} (0) = 1. \end{eqnarray}
\begin{eqnarray} \delta &\,=\,& 0.05,\ 0.06,\ 0.07, \nonumber \\ \frac {T_{\perp c}(0)}{T_{\parallel c}(0)} &\,=\,& \frac {\beta _{\perp c}(0)}{\beta _{\parallel c}(0)}= 1, \nonumber \\ \frac {T_{\perp h}(0)}{T_{\parallel h}(0)} &\,=\,& \frac {\beta _{\perp h}(0)}{\beta _{\parallel h}(0)} =9, \nonumber \\ \beta _{\parallel c} (0) &\,=\,& 1,\quad \beta _{\parallel h} (0) = 1. \end{eqnarray}

Figure 2. Effect of hot proton population on the dispersion properties of the PC mode: real oscillatory frequency,
![]() $\omega _r/\varOmega _p$
(top; solid), and growth rate,
$\omega _r/\varOmega _p$
(top; solid), and growth rate,
![]() $\gamma _k/\varOmega _{p}$
(bottom; dashed), versus normalised wavenumber,
$\gamma _k/\varOmega _{p}$
(bottom; dashed), versus normalised wavenumber,
![]() $ck/\omega _{p}$
, for different combinations of hot proton relative density values.
$ck/\omega _{p}$
, for different combinations of hot proton relative density values.
Physical quantities plotted along the x axis and along the y axis are the same as those in figure 1. Variations in the relative hot proton density,
![]() $\delta$
, and other fixed parameters are given in the figure title and within the plot. We note an enhancement of the real oscillatory frequency for the higher hot proton population case. Shown in the bottom panel, we note a significant rise in the proton instability growth and instability domain for the initial higher hot proton relative density, i.e.
$\delta$
, and other fixed parameters are given in the figure title and within the plot. We note an enhancement of the real oscillatory frequency for the higher hot proton population case. Shown in the bottom panel, we note a significant rise in the proton instability growth and instability domain for the initial higher hot proton relative density, i.e.
![]() $\delta =0.07$
. Such a notable increase in the real (oscillatory) frequency and growth rate is contributed by the large free energy associated with higher hot proton population in the form of perpendicular temperature anisotropy.
$\delta =0.07$
. Such a notable increase in the real (oscillatory) frequency and growth rate is contributed by the large free energy associated with higher hot proton population in the form of perpendicular temperature anisotropy.
As a result of PC instability, the velocity distributions of cold and hot protons evolve in time
![]() $t$
due to diffused pitch angle scattering in velocity space (Seough et al. Reference Seough, Yoon and cHwang2014; Kim Reference Kim, Hwang, Seough and Yoon2017). Quasilinear theory is one of the effective tools to quantify such a scattering phenomenon in the nonlinear regime of instability development. In response to the PC instability initiated by the hot proton anisotropy, the hot proton components cannot maintain the anisotropy level and saturate eventually at a certain lower magnitude. In figure 3 we uncover/quantify the effects of hot proton anisotropy variation on the initial forms of cold/hot proton velocity distributions and associated wave-energy density. To get quantitative predictions, we adopt the following set of initial parameters typical of magnetospheric conditions:
$t$
due to diffused pitch angle scattering in velocity space (Seough et al. Reference Seough, Yoon and cHwang2014; Kim Reference Kim, Hwang, Seough and Yoon2017). Quasilinear theory is one of the effective tools to quantify such a scattering phenomenon in the nonlinear regime of instability development. In response to the PC instability initiated by the hot proton anisotropy, the hot proton components cannot maintain the anisotropy level and saturate eventually at a certain lower magnitude. In figure 3 we uncover/quantify the effects of hot proton anisotropy variation on the initial forms of cold/hot proton velocity distributions and associated wave-energy density. To get quantitative predictions, we adopt the following set of initial parameters typical of magnetospheric conditions:
 \begin{eqnarray} W(k) &\,=\,& 5 \times 10^{-4},\quad \delta =0.07, \nonumber \\ \frac {T_{\perp c}(0)}{T_{\parallel c}(0)} &\,=\,& \frac {\beta _{\perp c}(0)}{\beta _{\parallel c}(0)}=1, \quad \beta _{\parallel c} (0) = 1, \nonumber \\ \frac {T_{\perp h}(0)}{T_{\parallel h}(0)} &\,=\,& \frac {\beta _{\perp h}(0)}{\beta _{\parallel h}(0)} =7,\mbox{ }8,\mbox{ }9, \quad \beta _{\parallel h} (0) = 1. \end{eqnarray}
\begin{eqnarray} W(k) &\,=\,& 5 \times 10^{-4},\quad \delta =0.07, \nonumber \\ \frac {T_{\perp c}(0)}{T_{\parallel c}(0)} &\,=\,& \frac {\beta _{\perp c}(0)}{\beta _{\parallel c}(0)}=1, \quad \beta _{\parallel c} (0) = 1, \nonumber \\ \frac {T_{\perp h}(0)}{T_{\parallel h}(0)} &\,=\,& \frac {\beta _{\perp h}(0)}{\beta _{\parallel h}(0)} =7,\mbox{ }8,\mbox{ }9, \quad \beta _{\parallel h} (0) = 1. \end{eqnarray}

Figure 3. The PC instability in the quasilinear regime: effect of hot proton anisotropy on time evolution in temperature (beta) for cold proton component,
![]() $\beta _{\perp c}$
and
$\beta _{\perp c}$
and
![]() $\beta _{\parallel c}$
(top), hot proton component,
$\beta _{\parallel c}$
(top), hot proton component,
![]() $\beta _{\perp h}$
and
$\beta _{\perp h}$
and
![]() $\beta _{\parallel h}$
(middle), and wave intensity,
$\beta _{\parallel h}$
(middle), and wave intensity,
![]() $\delta B^2/B_0^2$
(bottom), versus normalised time,
$\delta B^2/B_0^2$
(bottom), versus normalised time,
![]() $\tau =\varOmega _pt$
.
$\tau =\varOmega _pt$
.
In figure 3, the leftmost column adopts the initial parameters of
![]() $T_{\perp c}(0)/T_{\parallel c}(0)=1$
,
$T_{\perp c}(0)/T_{\parallel c}(0)=1$
,
![]() $\beta _{\parallel c}(0)=1$
, and
$\beta _{\parallel c}(0)=1$
, and
![]() $T_{\perp h}(0)/T_{\parallel h}(0)=5$
,
$T_{\perp h}(0)/T_{\parallel h}(0)=5$
,
![]() $\beta _{\parallel h}(0)=1$
; the middle column initial values of
$\beta _{\parallel h}(0)=1$
; the middle column initial values of
![]() $T_{\perp c}(0)/T_{\parallel c}(0)=1$
,
$T_{\perp c}(0)/T_{\parallel c}(0)=1$
,
![]() $\beta _{\parallel c}(0)=1$
, and
$\beta _{\parallel c}(0)=1$
, and
![]() $T_{\perp h}(0)/T_{\parallel h}(0)=7$
,
$T_{\perp h}(0)/T_{\parallel h}(0)=7$
,
![]() $\beta _{\parallel h}(0)=1$
; and the rightmost column initial parameters of
$\beta _{\parallel h}(0)=1$
; and the rightmost column initial parameters of
![]() $T_{\perp c}(0)/T_{\parallel c}(0)=1$
,
$T_{\perp c}(0)/T_{\parallel c}(0)=1$
,
![]() $\beta _{\parallel c}(0)=1$
, and
$\beta _{\parallel c}(0)=1$
, and
![]() $T_{\perp h}(0)/T_{\parallel h}(0)=9$
,
$T_{\perp h}(0)/T_{\parallel h}(0)=9$
,
![]() $\beta _{\parallel h}(0)=1$
. Vertical axis represents the profiles of time-varying core proton plasma betas,
$\beta _{\parallel h}(0)=1$
. Vertical axis represents the profiles of time-varying core proton plasma betas,
![]() $\beta _{\perp c},\beta _{\parallel c}$
, in the top row; hot proton plasma betas,
$\beta _{\perp c},\beta _{\parallel c}$
, in the top row; hot proton plasma betas,
![]() $\beta _{\perp h},\beta _{\parallel h}$
, in the middle row; and associated wave-energy density,
$\beta _{\perp h},\beta _{\parallel h}$
, in the middle row; and associated wave-energy density,
![]() $\delta B^2/B_0^2$
, in the bottom row. To quantify the time intervals for the saturation of particle distribution and wave intensity, we define a dimensionless quantity
$\delta B^2/B_0^2$
, in the bottom row. To quantify the time intervals for the saturation of particle distribution and wave intensity, we define a dimensionless quantity
![]() $\tau =\varOmega _p t$
(time normalised with PC frequency) along the horizontal direction for all cases. Based on the observations of the Earth’s outer magnetospheric regions (Gary et al. Reference Gary, Moldwin, Thomsen, Winske and Mccomas1994, Reference Gary, Thomsen, Yin and Winske1995), we keep the cold proton beta, hot proton beta, cold proton anisotropy and relative density of hot protons as fixed, i.e
$\tau =\varOmega _p t$
(time normalised with PC frequency) along the horizontal direction for all cases. Based on the observations of the Earth’s outer magnetospheric regions (Gary et al. Reference Gary, Moldwin, Thomsen, Winske and Mccomas1994, Reference Gary, Thomsen, Yin and Winske1995), we keep the cold proton beta, hot proton beta, cold proton anisotropy and relative density of hot protons as fixed, i.e
![]() $\beta _{\parallel c}=1,\beta _{\parallel h}=1,T_{\perp c}/T_{\parallel c}=1$
and
$\beta _{\parallel c}=1,\beta _{\parallel h}=1,T_{\perp c}/T_{\parallel c}=1$
and
![]() $\delta =0.05$
, respectively, for all our numerically executed output. Shown in the upper panel of the leftmost column, initially isotropic cold protons develop anisotropy, although minimal, through the perpendicular heating (see the gradual rise in
$\delta =0.05$
, respectively, for all our numerically executed output. Shown in the upper panel of the leftmost column, initially isotropic cold protons develop anisotropy, although minimal, through the perpendicular heating (see the gradual rise in
![]() $\beta _{\perp c}$
) and concomitantly parallel cooling (shown by the smooth falling of
$\beta _{\perp c}$
) and concomitantly parallel cooling (shown by the smooth falling of
![]() $\beta _{\parallel c}$
). In the resonant velocity space, isotropic protons get pitch-angle-scattered through diffusion and end up with some anisotropy in the nonlinear phase of PC instability. Below the cold protons, i.e middle panel of the leftmost column, we note a smooth transit of initially anisotropic hot protons to nearly isotropic state through perpendicular cooling, i.e. fall of
$\beta _{\parallel c}$
). In the resonant velocity space, isotropic protons get pitch-angle-scattered through diffusion and end up with some anisotropy in the nonlinear phase of PC instability. Below the cold protons, i.e middle panel of the leftmost column, we note a smooth transit of initially anisotropic hot protons to nearly isotropic state through perpendicular cooling, i.e. fall of
![]() $\beta _{\perp h}$
, and parallel heating, i.e rise in
$\beta _{\perp h}$
, and parallel heating, i.e rise in
![]() $\beta _{\parallel h}$
(an opposite effect compared with cold protons). At resonance, hot protons with higher perpendicular velocities get significantly scattered to end up with a nearly Maxwellian form in the interval
$\beta _{\parallel h}$
(an opposite effect compared with cold protons). At resonance, hot protons with higher perpendicular velocities get significantly scattered to end up with a nearly Maxwellian form in the interval
![]() $\tau =[600{-}1000]$
. In the bottom, we plot wave-energy density to confirm the possible plateau formation of the initial distribution of hot protons. We observe an exponential rise of the wave intensity from its initial noise level which cuts in the interval
$\tau =[600{-}1000]$
. In the bottom, we plot wave-energy density to confirm the possible plateau formation of the initial distribution of hot protons. We observe an exponential rise of the wave intensity from its initial noise level which cuts in the interval
![]() $\tau =[250{-}350]$
. Afterwards, we also note a reabsorption and regain in the wave intensity until the terminal point of the simulation. Moving on to the middle and rightmost panels, we adopt a relatively higher proton anisotropy ratio, i.e
$\tau =[250{-}350]$
. Afterwards, we also note a reabsorption and regain in the wave intensity until the terminal point of the simulation. Moving on to the middle and rightmost panels, we adopt a relatively higher proton anisotropy ratio, i.e
![]() $T_{\perp h}/T_{\parallel h}= 7$
(middle) and
$T_{\perp h}/T_{\parallel h}= 7$
(middle) and
![]() $T_{\perp h}/T_{\parallel h}=9$
(right), keeping other initial parameters fixed. The immediate outcomes of such changes appear in the form of speedy recovery/saturation of hot proton anisotropy, i.e
$T_{\perp h}/T_{\parallel h}=9$
(right), keeping other initial parameters fixed. The immediate outcomes of such changes appear in the form of speedy recovery/saturation of hot proton anisotropy, i.e
![]() $\tau =[180{-}210]$
in the middle panels and
$\tau =[180{-}210]$
in the middle panels and
![]() $\tau =[160{-}200]$
for the rightmost panels. We also note a quick response of cold protons to attain the anisotropy values on the earlier time scales. Similarly, the associated wave-energy density also displays drastic revisions in response to the new hot proton anisotropy. We display a relatively fast saturation and higher intensity cut levels in the middle and right panels compared with left ones. Such important changes in the particle–wave dynamics (excitation and saturation) are attributed to the availability of more free energy to initiate the PC instability and higher proton scattering through diffusion in velocity space.
$\tau =[160{-}200]$
for the rightmost panels. We also note a quick response of cold protons to attain the anisotropy values on the earlier time scales. Similarly, the associated wave-energy density also displays drastic revisions in response to the new hot proton anisotropy. We display a relatively fast saturation and higher intensity cut levels in the middle and right panels compared with left ones. Such important changes in the particle–wave dynamics (excitation and saturation) are attributed to the availability of more free energy to initiate the PC instability and higher proton scattering through diffusion in velocity space.
Like the real oscillatory frequency and growth rate of the PC mode, hot proton density also affects the relaxation/saturation of the proton distribution and resulting wave-energy density. To quantify the role of varying hot proton population in the wave dynamics, we sketch figure 4 based on the following set of initial conditions:
 \begin{eqnarray} W(k) &\,=\,& 5 \times 10^{-4}, \nonumber \\ \delta &\,=\,& 0.05,\ 0.06,\ 0.07, \nonumber \\ \frac {T_{\perp c}(0)}{T_{\parallel c}(0)} &\,=\,& \frac {\beta _{\perp c}(0)}{\beta _{\parallel c}(0)}=1, \quad \beta _{\parallel c} (0) = 1, \nonumber \\ \frac {T_{\perp h}(0)}{T_{\parallel h}(0)} &\,=\,& \frac {\beta _{\perp h}(0)}{\beta _{\parallel h}(0)} =9, \quad \beta _{\parallel h} (0) = 1. \end{eqnarray}
\begin{eqnarray} W(k) &\,=\,& 5 \times 10^{-4}, \nonumber \\ \delta &\,=\,& 0.05,\ 0.06,\ 0.07, \nonumber \\ \frac {T_{\perp c}(0)}{T_{\parallel c}(0)} &\,=\,& \frac {\beta _{\perp c}(0)}{\beta _{\parallel c}(0)}=1, \quad \beta _{\parallel c} (0) = 1, \nonumber \\ \frac {T_{\perp h}(0)}{T_{\parallel h}(0)} &\,=\,& \frac {\beta _{\perp h}(0)}{\beta _{\parallel h}(0)} =9, \quad \beta _{\parallel h} (0) = 1. \end{eqnarray}

Figure 4. The PC instability in the quasilinear regime: effect of hot proton relative density on time evolution in temperature (beta) for cold proton component,
![]() $\beta _{\perp c}$
and
$\beta _{\perp c}$
and
![]() $\beta _{\parallel c}$
(top), hot proton component,
$\beta _{\parallel c}$
(top), hot proton component,
![]() $\beta _{\perp h}$
and
$\beta _{\perp h}$
and
![]() $\beta _{\parallel h}$
(middle), and wave intensity,
$\beta _{\parallel h}$
(middle), and wave intensity,
![]() $\delta B^2/B_0^2$
(bottom), versus normalised time,
$\delta B^2/B_0^2$
(bottom), versus normalised time,
![]() $\tau =\varOmega _pt$
.
$\tau =\varOmega _pt$
.
In figure 4, the leftmost column is plotted with initial conditions of of
![]() $\delta =0.04$
,
$\delta =0.04$
,
![]() $T_{\perp c}(0)/T_{\parallel c}(0)=1$
,
$T_{\perp c}(0)/T_{\parallel c}(0)=1$
,
![]() $\beta _{\parallel c}(0)=1$
, and
$\beta _{\parallel c}(0)=1$
, and
![]() $T_{\perp h}(0)/T_{\parallel h}(0)=7$
,
$T_{\perp h}(0)/T_{\parallel h}(0)=7$
,
![]() $\beta _{\parallel h}(0)=1$
; the middle column with initial values of
$\beta _{\parallel h}(0)=1$
; the middle column with initial values of
![]() $\delta =0.06$
,
$\delta =0.06$
,
![]() $T_{\perp c}(0)/T_{\parallel c}(0)=1$
,
$T_{\perp c}(0)/T_{\parallel c}(0)=1$
,
![]() $\beta _{\parallel c}(0)=1$
, and
$\beta _{\parallel c}(0)=1$
, and
![]() $T_{\perp h}(0)/T_{\parallel h}(0)=7$
,
$T_{\perp h}(0)/T_{\parallel h}(0)=7$
,
![]() $\beta _{\parallel h}(0)=1$
; and the rightmost column with initial parameters of
$\beta _{\parallel h}(0)=1$
; and the rightmost column with initial parameters of
![]() $\delta =0.08$
,
$\delta =0.08$
,
![]() $T_{\perp c}(0)/T_{\parallel c}(0)=1$
,
$T_{\perp c}(0)/T_{\parallel c}(0)=1$
,
![]() $\beta _{\parallel c}(0)=1$
, and
$\beta _{\parallel c}(0)=1$
, and
![]() $T_{\perp h}(0)/T_{\parallel h}(0)\,{=}\,7$
,
$T_{\perp h}(0)/T_{\parallel h}(0)\,{=}\,7$
,
![]() $\beta _{\parallel h}(0)=1$
,
$\beta _{\parallel h}(0)=1$
,
![]() $\beta _{\parallel h}(0)=0.6$
. Such a combination of input conditions is also typical of magnetospheric plasma conditions. We make a choice of fixed anisotropy ratio and plasma betas of constituent proton components as indicated in (3.7). Labelling and variation of beta profiles largely resemble the results displayed in figure 2. As the PC instability evolves in time
$\beta _{\parallel h}(0)=0.6$
. Such a combination of input conditions is also typical of magnetospheric plasma conditions. We make a choice of fixed anisotropy ratio and plasma betas of constituent proton components as indicated in (3.7). Labelling and variation of beta profiles largely resemble the results displayed in figure 2. As the PC instability evolves in time
![]() $t$
, the initial isotropic cold protons attain a certain anisotropy magnitude following a perpendicular rise (heating) in
$t$
, the initial isotropic cold protons attain a certain anisotropy magnitude following a perpendicular rise (heating) in
![]() $\beta _{\perp c}$
and concomitantly fall (or cooling) in
$\beta _{\perp c}$
and concomitantly fall (or cooling) in
![]() $\beta _{\parallel c}$
shown in the leftmost top panel. On the other hand, hot protons displayed in the middle panel (leftmost) tend to relax their initial anisotropy level with a gradual fall in
$\beta _{\parallel c}$
shown in the leftmost top panel. On the other hand, hot protons displayed in the middle panel (leftmost) tend to relax their initial anisotropy level with a gradual fall in
![]() $\beta _{\perp h}$
and rise in the opposite direction, i.e.
$\beta _{\perp h}$
and rise in the opposite direction, i.e.
![]() $\beta _{\parallel h}$
. We note a similar time interval of
$\beta _{\parallel h}$
. We note a similar time interval of
![]() $\tau =[200{-}300]$
to develop the anisotropy of cold protons and saturation/relaxation of the hot protons. The wave-energy density increases at initial time which eventually saturates following the hot proton relaxation time intervals. For the initial higher hot proton population (results displayed in middle and rightmost panels), we note an appreciable rise in the wave-intensity saturation and speedy recovery of hot protons towards a lower anisotropy ratio. Such an important outcome signifies the greater free energy associated with large anisotropic hot proton density.
$\tau =[200{-}300]$
to develop the anisotropy of cold protons and saturation/relaxation of the hot protons. The wave-energy density increases at initial time which eventually saturates following the hot proton relaxation time intervals. For the initial higher hot proton population (results displayed in middle and rightmost panels), we note an appreciable rise in the wave-intensity saturation and speedy recovery of hot protons towards a lower anisotropy ratio. Such an important outcome signifies the greater free energy associated with large anisotropic hot proton density.
The role of PC instability in constraining the high perpendicular temperature is displayed again in figure 5. We replot the findings of figure 3 in the phase space formed by the plasma beta,
![]() $\beta _{\parallel }$
, and temperature anisotropy,
$\beta _{\parallel }$
, and temperature anisotropy,
![]() $T_\perp /T_\parallel$
. Guided by the results of Shaaban et al. (Reference Shaaban, Lazar, Poedts and Elhanbaly2016), we have differentiated the stable versus unstable part for the proton states. We show the dynamical trajectories of initial unstable hot protons towards stable regions. Wave-energy density associated with unstable PC instability is depicted with colour code shown in the vertical bar. Evident from the plot, isotropic cold protons attain a certain anisotropy as a result of wave–particle interaction and settle down within the stable part of the plot. Higher anisotropy of hot protons is compensated with excitation of PC instability and a move towards the stable region. They are relocated well below the marginal stability curves with relatively lower anisotropy compared with their initial positions. Through the perpendicular cooling and parallel heating resulting from PC, proton trajectories are significantly influenced in phase space. Notably, the relaxation process for hot protons with high initial anisotropy is relatively rapid, especially at elevated wave-energy densities, which are illustrated in colour coding along the dynamic paths. As shown in figure 5, initially isotropic protons achieve similar temperature anisotropies and occupy comparable states of anisotropy in phase space. In contrast to hot protons, cold protons experience perpendicular heating and cool along the magnetic field during resonant interactions with cyclotron instability. Additionally, the response of cold protons is abrupt, with a large associated energy density indicated in the right-hand vertical bar. Such an important behaviour of cold/hot protons can also be attributed to the PC instability driven unstable solely by the tenuous hot proton component. Figure 5, therefore, provides a rapid demonstration to unlock the important role of PC instability in defining the perpendicular temperature of hot protons in the magnetospheric regions of space plasmas.
$T_\perp /T_\parallel$
. Guided by the results of Shaaban et al. (Reference Shaaban, Lazar, Poedts and Elhanbaly2016), we have differentiated the stable versus unstable part for the proton states. We show the dynamical trajectories of initial unstable hot protons towards stable regions. Wave-energy density associated with unstable PC instability is depicted with colour code shown in the vertical bar. Evident from the plot, isotropic cold protons attain a certain anisotropy as a result of wave–particle interaction and settle down within the stable part of the plot. Higher anisotropy of hot protons is compensated with excitation of PC instability and a move towards the stable region. They are relocated well below the marginal stability curves with relatively lower anisotropy compared with their initial positions. Through the perpendicular cooling and parallel heating resulting from PC, proton trajectories are significantly influenced in phase space. Notably, the relaxation process for hot protons with high initial anisotropy is relatively rapid, especially at elevated wave-energy densities, which are illustrated in colour coding along the dynamic paths. As shown in figure 5, initially isotropic protons achieve similar temperature anisotropies and occupy comparable states of anisotropy in phase space. In contrast to hot protons, cold protons experience perpendicular heating and cool along the magnetic field during resonant interactions with cyclotron instability. Additionally, the response of cold protons is abrupt, with a large associated energy density indicated in the right-hand vertical bar. Such an important behaviour of cold/hot protons can also be attributed to the PC instability driven unstable solely by the tenuous hot proton component. Figure 5, therefore, provides a rapid demonstration to unlock the important role of PC instability in defining the perpendicular temperature of hot protons in the magnetospheric regions of space plasmas.

Figure 5. Combined particle–wave evolution in response to the PC instability: magnetospheric cold and hot proton trajectories from initial to final positions in the phase space formed by
![]() $T_\perp /T_\parallel$
and
$T_\perp /T_\parallel$
and
![]() $\beta _\parallel$
. We have colour-coded the resulting wave-energy density as indicated in the sidebar.
$\beta _\parallel$
. We have colour-coded the resulting wave-energy density as indicated in the sidebar.
4. Summary and discussion
Various space plasma dynamics, e.g. solar wind and Earth’s magnetosphere, are governed/dictated by collective and collisional physical mechanisms. Under certain geometrical and thermal conditions, microinstabilities resulting from the collective processes solely predict and determine charged particle states. Our present study predicts the key role of PC instability in constraining the rapid rise in the perpendicular temperature and defines the threshold values of the unstable PC mode. This instability is left-hand-polarised and operative under high perpendicular temperature, i.e.
![]() $T_{\perp p}\gt T_{\parallel p}$
. Such a combination of initial conditions is frequently observed in magnetospheric regions by different space missions and motivates us to find the effective contribution of PC instability. Observations made over the years in magnetospheric regions (Gary et al. Reference Gary, Moldwin, Thomsen, Winske and Mccomas1994, Reference Gary, Thomsen, Yin and Winske1995; Toledo et al. Reference Toledo-Redondo2021; Liu et al. Reference Liu2024) suggest adopting multi-component cold and hot proton species. We model the anisotropic hot protons with the bi-Maxwellian form of the velocity distribution. We further assume time variations in the initial isotropic temperature of cold protons and anisotropic temperature of hot protons to study the detailed dynamics of the instability in the quasilinear regime. Different simulation studies appearing in the literature validate and confirm our approximations regarding the initial distribution.
$T_{\perp p}\gt T_{\parallel p}$
. Such a combination of initial conditions is frequently observed in magnetospheric regions by different space missions and motivates us to find the effective contribution of PC instability. Observations made over the years in magnetospheric regions (Gary et al. Reference Gary, Moldwin, Thomsen, Winske and Mccomas1994, Reference Gary, Thomsen, Yin and Winske1995; Toledo et al. Reference Toledo-Redondo2021; Liu et al. Reference Liu2024) suggest adopting multi-component cold and hot proton species. We model the anisotropic hot protons with the bi-Maxwellian form of the velocity distribution. We further assume time variations in the initial isotropic temperature of cold protons and anisotropic temperature of hot protons to study the detailed dynamics of the instability in the quasilinear regime. Different simulation studies appearing in the literature validate and confirm our approximations regarding the initial distribution.
In the present study, we reveal the role of unstable PC instability in dictating the dynamics of outer magnetospheric regions. The choice of initial condition set-up composed of temperature anisotropy and plasma betas are typical of the Earth’s outer magnetosphere. We note an appreciable rise in the growth rate and the domain of the instability for large initial hot proton anisotropy and population. Quasilinear evolution of PC instability helps us to understand and quantify the wave-energy saturation and relaxation of hot proton temperatures. Higher temperature anisotropy and the number density of hot protons largely favour the relaxation/saturation mechanism and wave-energy density cutoffs. Such conclusions are attributed to the availability of more free energy (high temperature anisotropy and population of hot protons) to pump the instability and abruptly leads to isotropisation/relaxation. Dynamical paths in phase space show the final destinations of both core versus halo proton components near or below the marginal stability curves.
Our present analysis is limited to establishing a theoretical framework for the PC instability and its time evolution in the Earth’s outer magnetospheric environments. To validate such comprehensive results based on a mathematical model, a comparison against a more rigorous particle-in-cell simulation is called for. In some recent developments, side-by-side comparisons against simulation and observations are reported for the combined wave spectrum of electron-cyclotron mirror (Sarfraz et al. Reference Sarfraz, López, Ahmed and Yoon2022) and PC mirror (Yoon et al. Reference Yoon, Sarfraz, Ali, Salem and Seough2022). Observations are particularly attained via WIND spacecraft SWE Faraday cup observations (Ogilvie et al. Reference Ogilvie1995). For the other regions where observations suggest the presence of suprathermal charged particles, our present formalism can principally be extended to incorporate the non-thermal effects (Shaaban et al. Reference Shaaban, Lazar and Schlickeiser2021) and radial expansion effects too (Yoon & Sarfraz Reference Yoon and Sarfraz2017). One of the key perspectives is to extend such a scheme for oblique propagation and see its impact on the instability thresholds and possibly evolution in the quasilinear regime.
Acknowledgements
Editor Thierry Passot thanks the referees for their advice in evaluating this article.
Data availability statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Declaration of interests
The authors report no conflict of interest.