Article contents
Electron interactions and quantum plasma physics†
Published online by Cambridge University Press: 13 March 2009
Abstract
The ‘quantum electrodynamics’ of the scattering of radiation from a fully ionized, interacting plasma is to be considered.
The plasma particle interaction must properly be treated quantum mechanically when the electron plasma wave phonon energies are comparable to or greater than the mean random electron energies and/or when the phonon momenta are of the order of magnitude or greater than the average electron momenta in the plasma.
In these two circumstances or either one of them, the plasma particle inter action must be treated in a quantum mechanical manner. The ‘solid-state’ plasma recently discussed by D.E.McCumber is an example of a quantum plasma.
Whether a classical or a quantum plasma is considered, the collective properties, as well as the single-particle properties, need to be considered. The collective properties of the plasma become important when it interacts with a radiation field in the case where the electron plasma frequency, ωp, is of the same order of magnitude, or exceeds, the operating radiation frequency ω, i.e. ωp≥ω.
A criterion to distinguish the properties of a plasma as to whether it is classical or quantum mechanical in nature can be defined in terms of three fundamental lengths of the electron gas. These definitions hold for a one-component plasma. They are: the classical length βe2, the Debye screening length 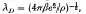 and the thermal de Broglie wavelength
and the thermal de Broglie wavelength 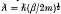 defined as 1/kT. From these three quantities, we can define two dimensionless parameters. They are the classical parameter
defined as 1/kT. From these three quantities, we can define two dimensionless parameters. They are the classical parameter 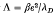 and the quantum parameter δ=λ/λD which is a measure of the quantum effects. For a quantum plasma δ>1 and in the classical limit (h = 0),δ=0, Λ<1.
and the quantum parameter δ=λ/λD which is a measure of the quantum effects. For a quantum plasma δ>1 and in the classical limit (h = 0),δ=0, Λ<1.
When we take into account the collective behaviour characterized by the plasma oscillations, screening effects are an automatic aspect of the electron plasma gas.
It is hoped that the present review article will provide the background material for general understanding of the field and easy access to the current literature. It is also hoped that the present discussion will establish greater interest in this subject.
As an example of a calculation of plasma properties, a calculation of the generalized dielectric constant for both a low-density plasma in the classical limit and a high-density plasma in the quantum mechanical limit is performed and compared in a suitable manner.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 1968
References
REFERENCES
- 9
- Cited by

