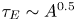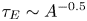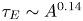1. Introduction
While most current devices use deuterium as an operating main plasma species, an eventual reactor will use deuterium–tritium mixtures. This has motivated several experimental studies (many historic) on the effects of the main species isotope on plasma properties, albeit restricted to comparisons between deuterium and hydrogen, except for JET-C (Bessenrodt-Weberpals, Wagner & ASDEX Team Reference Bessenrodt-Weberpals and Wagner1993; Cordey et al. Reference Cordey, Balet, Bartlett, Budnya, Christiansen, Conway, Eriksson, Fishpool, Gowers and De Haas1999; JET Team 1999; Saibene et al. Reference Saibene, Horton, Sartori, Balet, Clement, Conway, Cordey, De Esch, Ingesson and Lingertat1999; Maggi et al. Reference Maggi, Weisen, Hillesheim, Chankin, Delabie, Horvath, Auriemma, Carvalho, Corrigan and Flanagan2018, Reference Maggi, Weisen, Casson, Auriemma, Lorenzini, Nordman, Delabie, Eriksson, Flanagan and Keeling2019; Weisen et al. Reference Weisen, Maggi, Menmuir, Horvath, Bache, Casson, Oberparleiter, Saarelma, Auriemma and Chankin2018), and TFTR (Scott et al. Reference Scott, Zarnstorff, Barnes, Bell, Bretz, Bush, Chang, Ernst, Fonck and Johnson1995; Ernst et al. Reference Ernst, Coppi, Scott and Porkolab1998). We will refer to JET as JET-C for the period when JET was operated with carbon plasma facing components, i.e. up to 2009 and as JET-ILW beyond 2010, when JET was equipped with a tungsten divertor and Be main chamber limiters (Matthews et al. Reference Matthews, Beurskens, Brezinsek, Groth, Joffrin, Loving, Kear, Mayoral, Neu and Prior2011).
In early experiments in ASDEX and in several other devices, thoroughly reviewed in Reference Bessenrodt-Weberpals and WagnerBessenrodt-Weberpals, very significant positive dependencies on the isotope mass were observed. Deuterium plasmas in ASDEX had significantly better confinement than hydrogen plasmas in all confinement regimes and heating modes. Indeed, some improved confinement regimes were inaccessible with hydrogen operation [Reference Bessenrodt-Weberpals and WagnerBessenrodt]. Deuterium H-modes in ASDEX were reported to have a confinement time twice that of H-modes in hydrogen, while in L-mode the improvement was weaker, but still substantial (a factor 1.4). TFTR reported a strong L-mode scaling of the thermal confinement time ![]() ${\tau _E} = {W_{\textrm{tot}}}/{P_{\textrm{loss}}}\propto {A^{0.5}}$ (Scott et al. Reference Scott, Zarnstorff, Barnes, Bell, Bretz, Bush, Chang, Ernst, Fonck and Johnson1995), and a very strong scaling in the supershot regime
${\tau _E} = {W_{\textrm{tot}}}/{P_{\textrm{loss}}}\propto {A^{0.5}}$ (Scott et al. Reference Scott, Zarnstorff, Barnes, Bell, Bretz, Bush, Chang, Ernst, Fonck and Johnson1995), and a very strong scaling in the supershot regime ![]() ${\tau _E}\propto {A^{0.85}}$ (Ernst et al. Reference Ernst, Coppi, Scott and Porkolab1998), based on a comparison of deuterium and deuterium–tritium mixtures. Here, A is the atomic mass number,
${\tau _E}\propto {A^{0.85}}$ (Ernst et al. Reference Ernst, Coppi, Scott and Porkolab1998), based on a comparison of deuterium and deuterium–tritium mixtures. Here, A is the atomic mass number, ![]() ${W_{\textrm{tot}}} = 1.5\int {( {n_e}{T_e} + {n_i}{T_i}) \,\textrm{d}V}$, the thermal stored energy, P loss is the power transported through the last closed flux surface (LCFS), Te and Ti are the electron and ion temperatures, ne and ni being their densities (the integral in the above expression extends over the whole plasma volume).
${W_{\textrm{tot}}} = 1.5\int {( {n_e}{T_e} + {n_i}{T_i}) \,\textrm{d}V}$, the thermal stored energy, P loss is the power transported through the last closed flux surface (LCFS), Te and Ti are the electron and ion temperatures, ne and ni being their densities (the integral in the above expression extends over the whole plasma volume).
The popular IPB98(y,2) ELMy (i.e. exhibiting regular relaxations of the edge transport barrier due to edge localised modes) H-mode thermal energy scaling (ITER Physics Basis 1999; Doyle Reference Doyle, Houlberg, Kamada, Mukhovatov, Osborne, Polevoi, Bateman, Connor, Cordey and Fujita2007), the underlying dataset of which includes data from tritium and deuterium–tritium mixtures from the JET-C DTE1 campaign (Saibene et al. Reference Saibene, Horton, Sartori, Balet, Clement, Conway, Cordey, De Esch, Ingesson and Lingertat1999) in 1997 exhibit, however, only a weak scaling, ![]() ${\tau _E}\propto {A^{0.19}}$. This is close to the one for L-mode,
${\tau _E}\propto {A^{0.19}}$. This is close to the one for L-mode, ![]() ${\tau _E}\propto {A^{0.2}}$ (ITER Physics Basis 1999). The weak ELMy H-mode scaling contrasts with a relatively strong scaling of the ELM-free confinement time reported in ITER Physics Basis (1999),
${\tau _E}\propto {A^{0.2}}$ (ITER Physics Basis 1999). The weak ELMy H-mode scaling contrasts with a relatively strong scaling of the ELM-free confinement time reported in ITER Physics Basis (1999), ![]() ${\tau _E}\propto {A^{0.43}}$, hinting at the role of the H-mode edge pedestal. While global scaling from international databases (ITER Physics Basis 1999; Doyle Reference Doyle, Houlberg, Kamada, Mukhovatov, Osborne, Polevoi, Bateman, Connor, Cordey and Fujita2007; Verdoolaege et al. Reference Verdoolaege, Kaye, Angioni, Kardaun, Ryter, Thomsen, Maslov and Romanelli2018) use very diverse datasets, which are susceptible to correlations between scaling variables, experiments with matched or at least similar sets of data with different species can provide different results. This was the case of the global confinement time of a small set of JET-C pulses of similar density in H, D and T, for which no significant isotope dependence was found:
${\tau _E}\propto {A^{0.43}}$, hinting at the role of the H-mode edge pedestal. While global scaling from international databases (ITER Physics Basis 1999; Doyle Reference Doyle, Houlberg, Kamada, Mukhovatov, Osborne, Polevoi, Bateman, Connor, Cordey and Fujita2007; Verdoolaege et al. Reference Verdoolaege, Kaye, Angioni, Kardaun, Ryter, Thomsen, Maslov and Romanelli2018) use very diverse datasets, which are susceptible to correlations between scaling variables, experiments with matched or at least similar sets of data with different species can provide different results. This was the case of the global confinement time of a small set of JET-C pulses of similar density in H, D and T, for which no significant isotope dependence was found: ![]() ${\tau _E}\propto {A^{0.03}}$ (Cordey et al. Reference Cordey, Balet, Bartlett, Budnya, Christiansen, Conway, Eriksson, Fishpool, Gowers and De Haas1999). Two term scalings, separating core and pedestal thermal confinement in the H-mode, have been reported to have a very strong pedestal scaling
${\tau _E}\propto {A^{0.03}}$ (Cordey et al. Reference Cordey, Balet, Bartlett, Budnya, Christiansen, Conway, Eriksson, Fishpool, Gowers and De Haas1999). Two term scalings, separating core and pedestal thermal confinement in the H-mode, have been reported to have a very strong pedestal scaling ![]() ${\tau _{E, \textrm{ped}}}\propto {A^{0.96}}$ and a weak negative dependence of the plasma core confinement
${\tau _{E, \textrm{ped}}}\propto {A^{0.96}}$ and a weak negative dependence of the plasma core confinement ![]() ${\tau _{E, \textrm{core}}}\propto {A^{ - 0.16}}$ (Cordey et al. Reference Cordey, Balet, Bartlett, Budnya, Christiansen, Conway, Eriksson, Fishpool, Gowers and De Haas1999). Here,
${\tau _{E, \textrm{core}}}\propto {A^{ - 0.16}}$ (Cordey et al. Reference Cordey, Balet, Bartlett, Budnya, Christiansen, Conway, Eriksson, Fishpool, Gowers and De Haas1999). Here, ![]() ${\tau _{E, \textrm{ped}}} = {W_{\textrm{ped}}}/{P_{\textrm{loss}}}$, with
${\tau _{E, \textrm{ped}}} = {W_{\textrm{ped}}}/{P_{\textrm{loss}}}$, with ![]() ${W_{\textrm{ped}}} = 1.5( {n_{e\,\textrm{ped}}}{T_{e\,\textrm{ped}}} + {n_{i\,\textrm{ped}}}{T_{i\,\textrm{ped}}}) {V_{\textrm{top}}}$ where subscript ped refers to the values at the pedestal top, which is typically 1–3 cm inward from the LCFS in JET (Maggi et al. Reference Maggi, Frassinetti, Horvath, Lunniss, Saarelma, Wilson, Flanagan, Leyland, Lupelli and Pamela2017),
${W_{\textrm{ped}}} = 1.5( {n_{e\,\textrm{ped}}}{T_{e\,\textrm{ped}}} + {n_{i\,\textrm{ped}}}{T_{i\,\textrm{ped}}}) {V_{\textrm{top}}}$ where subscript ped refers to the values at the pedestal top, which is typically 1–3 cm inward from the LCFS in JET (Maggi et al. Reference Maggi, Frassinetti, Horvath, Lunniss, Saarelma, Wilson, Flanagan, Leyland, Lupelli and Pamela2017), ![]() ${V_{\textrm{top}}} \approx V$ is the volume inside the flux surface defined by the pedestal top and V the total plasma volume. The core confinement time is defined as
${V_{\textrm{top}}} \approx V$ is the volume inside the flux surface defined by the pedestal top and V the total plasma volume. The core confinement time is defined as ![]() ${\tau _{E, \textrm{core}}} = {\tau _E} - {\tau _{E, \textrm{ped}}}$. The scalings reported by Cordey et al. (Reference Cordey, Balet, Bartlett, Budnya, Christiansen, Conway, Eriksson, Fishpool, Gowers and De Haas1999) are at odds with more recent experimental results (Maggi et al. Reference Maggi, Weisen, Hillesheim, Chankin, Delabie, Horvath, Auriemma, Carvalho, Corrigan and Flanagan2018) and the now well documented and understood transport property of profile stiffness (Garbet et al. Reference Garbet, Mantica, Ryter, Cordey, Imbeaux, Sozzi, Manini, Asp, Parail and Wolf2004; Citrin et al. Reference Citrin, Jenko, Mantica, Told, Bourdelle, Dumont, Garcia, Haverkort, Hogeweij, Johnson and Pueschel2014). Profile stiffness, leads to a proportionality of the total thermal stored energy content and the pedestal thermal energy content, i.e.
${\tau _{E, \textrm{core}}} = {\tau _E} - {\tau _{E, \textrm{ped}}}$. The scalings reported by Cordey et al. (Reference Cordey, Balet, Bartlett, Budnya, Christiansen, Conway, Eriksson, Fishpool, Gowers and De Haas1999) are at odds with more recent experimental results (Maggi et al. Reference Maggi, Weisen, Hillesheim, Chankin, Delabie, Horvath, Auriemma, Carvalho, Corrigan and Flanagan2018) and the now well documented and understood transport property of profile stiffness (Garbet et al. Reference Garbet, Mantica, Ryter, Cordey, Imbeaux, Sozzi, Manini, Asp, Parail and Wolf2004; Citrin et al. Reference Citrin, Jenko, Mantica, Told, Bourdelle, Dumont, Garcia, Haverkort, Hogeweij, Johnson and Pueschel2014). Profile stiffness, leads to a proportionality of the total thermal stored energy content and the pedestal thermal energy content, i.e. ![]() ${W_{\textrm{tot}}} = \propto {W_{\textrm{ped}}}$. Here, ne and ni are the local electron and ion densities, Te and Ti their temperatures; the integral extends over the plasma volume and P loss is the power transported by the plasma through the separatrix. (In the above expression we have neglected the fact that the pedestal top is typically 1–3 cm inward from the separatrix.) Core ion profile stiffness can however be broken, generally with high neutral beam heating (NBH) power, by core transport processes such as E × B defined earlier shear stabilisation (Hahm & Burrell Reference Hahm and Burrell1995, Reference Hahm and Burrell1996; Rosenbluth & Hinton Reference Rosenbluth and Hinton1998; Waltz, Dewar & Garbet Reference Waltz, Dewar and Garbet1998; Biglari Reference Biglari, Diamond and Terry1990) and fast ion stabilisation (Citrin et al. Reference Citrin, Jenko, Mantica, Told, Bourdelle, Dumont, Garcia, Haverkort, Hogeweij, Johnson and Pueschel2014, Reference Citrin, Garcia, Görler, Jenko, Mantica, Told, Bourdelle, Hatch, Hogeweij and Johnson2015; Garcia et al. Reference Garcia, Challis, Citrin, Doerk, Giruzzi, Görler, Jenko and Maget2015; Di Siena et al. Reference Di Siena, Görler, Doerk, Bilato, Citrin, Johnson, Schneider and Poli2018) of ion temperature gradient modes (ITGs), leading to a core confinement improvement beyond that expected from the pedestal alone. The international ITPA confinement databases have recently been revised and now include new data in hydrogen from ASDEX-upgrade and JET-ILW (Verdoolaege et al. Reference Verdoolaege, Kaye, Angioni, Kardaun, Ryter, Thomsen, Maslov and Romanelli2018). Exponents for the isotope mass range from 0.09 to 0.47, depending on the datasets and regression methods used.
${W_{\textrm{tot}}} = \propto {W_{\textrm{ped}}}$. Here, ne and ni are the local electron and ion densities, Te and Ti their temperatures; the integral extends over the plasma volume and P loss is the power transported by the plasma through the separatrix. (In the above expression we have neglected the fact that the pedestal top is typically 1–3 cm inward from the separatrix.) Core ion profile stiffness can however be broken, generally with high neutral beam heating (NBH) power, by core transport processes such as E × B defined earlier shear stabilisation (Hahm & Burrell Reference Hahm and Burrell1995, Reference Hahm and Burrell1996; Rosenbluth & Hinton Reference Rosenbluth and Hinton1998; Waltz, Dewar & Garbet Reference Waltz, Dewar and Garbet1998; Biglari Reference Biglari, Diamond and Terry1990) and fast ion stabilisation (Citrin et al. Reference Citrin, Jenko, Mantica, Told, Bourdelle, Dumont, Garcia, Haverkort, Hogeweij, Johnson and Pueschel2014, Reference Citrin, Garcia, Görler, Jenko, Mantica, Told, Bourdelle, Hatch, Hogeweij and Johnson2015; Garcia et al. Reference Garcia, Challis, Citrin, Doerk, Giruzzi, Görler, Jenko and Maget2015; Di Siena et al. Reference Di Siena, Görler, Doerk, Bilato, Citrin, Johnson, Schneider and Poli2018) of ion temperature gradient modes (ITGs), leading to a core confinement improvement beyond that expected from the pedestal alone. The international ITPA confinement databases have recently been revised and now include new data in hydrogen from ASDEX-upgrade and JET-ILW (Verdoolaege et al. Reference Verdoolaege, Kaye, Angioni, Kardaun, Ryter, Thomsen, Maslov and Romanelli2018). Exponents for the isotope mass range from 0.09 to 0.47, depending on the datasets and regression methods used.
After the TFTR and JET-C D-T campaigns, isotope effects received little attention for an entire decade until experiments in JT-60 U with high quality diagnostics showed a clear dependence of the ion heat flux on the main isotope in H-mode, hydrogen plasmas requiring approximately twice as much power as deuterium plasmas in order to achieve the same stored energy (Urano et al. Reference Urano, Takizuka, Kikuchi, Nakano, Hayashi, Oyama and Kamada2012, Reference Urano, Takizuka, Aiba, Kikuchi, Nakano, Fujita, Oyama, Kamada and Hayashi2013).
Overall, these results have painted a rather confusing picture of the dependence of the energy confinement time on the isotope mass. The bewildering range of results reported suggests that what is commonly referred to as ‘isotope effects’ may result from a number of effects linked to the usage of different working gases as much as from intrinsic transport physics. However, what virtually all observations have in common is an improvement of global energy confinement with ion mass, in apparent contradiction with simple theoretical estimates, which predict gyroBohm scaling, i.e. ![]() ${\tau _E}\propto {A^{ - 1/2}}$ (Perkins et al. Reference Perkins, Barnes, Johnson, Scott, Zarnstorff, Bell, Bell, Bush, Grek and Hill1993). Some of the incongruities of early results may be linked diagnostics limitations, such as the lack of spatial resolution for resolving the H-mode pedestal. Diagnostic quality and the resolution for pedestal measurements has greatly improved since, as has our understanding of transport, prompting a revisit of the ‘isotope effect’ during the last decade in several devices.
${\tau _E}\propto {A^{ - 1/2}}$ (Perkins et al. Reference Perkins, Barnes, Johnson, Scott, Zarnstorff, Bell, Bell, Bush, Grek and Hill1993). Some of the incongruities of early results may be linked diagnostics limitations, such as the lack of spatial resolution for resolving the H-mode pedestal. Diagnostic quality and the resolution for pedestal measurements has greatly improved since, as has our understanding of transport, prompting a revisit of the ‘isotope effect’ during the last decade in several devices.
2. Effects depending on working gas isotope
2.1. Transport physics effects
There are numerous basic plasma parameters that depend on the ion mass number. These include the thermal velocity ![]() ${v_i} = {( {T_i}/{m_i}) ^{1/2}}$ where
${v_i} = {( {T_i}/{m_i}) ^{1/2}}$ where ![]() ${m_i} = A{m_p}$,
${m_i} = A{m_p}$, ![]() ${m_p}$ being the proton mass, the ion Larmor radius
${m_p}$ being the proton mass, the ion Larmor radius ![]() ${\rho _i} = {v_i}/{\omega _{\textrm{ci}}}, \;{\omega _{\textrm{ci}}} = ZeB/( A{m_p}) $ being the ion cyclotron frequency, the Alfvén velocity
${\rho _i} = {v_i}/{\omega _{\textrm{ci}}}, \;{\omega _{\textrm{ci}}} = ZeB/( A{m_p}) $ being the ion cyclotron frequency, the Alfvén velocity ![]() ${v_A} = B/{( {\mu _0}{n_i}{m_i}) ^{1/2}}$, the ion–ion collision frequency ν ii and electron–ion momentum and energy exchange frequencies ν ei and
${v_A} = B/{( {\mu _0}{n_i}{m_i}) ^{1/2}}$, the ion–ion collision frequency ν ii and electron–ion momentum and energy exchange frequencies ν ei and ![]() $v_{\textrm{ei}}^E$ (for a single ion species plasma).
$v_{\textrm{ei}}^E$ (for a single ion species plasma).
as well as the electron–ion heat exchange power density ![]() ${q_{\textrm{ei}}} = 1.5{n_e}\nu _{\textrm{ei}}^E( {T_e} - {T_i}) \propto {A^{ - 1}}$. In the above B is the magnetic field, ni is the ion density, Z the atomic charge number, ne the electron density,
${q_{\textrm{ei}}} = 1.5{n_e}\nu _{\textrm{ei}}^E( {T_e} - {T_i}) \propto {A^{ - 1}}$. In the above B is the magnetic field, ni is the ion density, Z the atomic charge number, ne the electron density, ![]() ${v_e} = {( {T_e}/{m_e}) ^{1/2}}$ the electron thermal velocity and ln Λ is the Coulomb logarithm (Huba Reference Huba2013).
${v_e} = {( {T_e}/{m_e}) ^{1/2}}$ the electron thermal velocity and ln Λ is the Coulomb logarithm (Huba Reference Huba2013).
We loosely follow Horton (Reference Horton1999) to introduce the basic expectation for the scaling of the cross-field diffusion coefficient D and heat diffusivity χ for drift wave turbulence ![]() $D \sim \chi \sim \Delta _r^2/\delta t$, where Δr is the characteristic turbulent radial scale length and
$D \sim \chi \sim \Delta _r^2/\delta t$, where Δr is the characteristic turbulent radial scale length and ![]() ${\delta _t} \approx {L_\theta }/{v_d} \approx {L_\theta }/( T/eZB{L_r}) $ its characteristic time scale,
${\delta _t} \approx {L_\theta }/{v_d} \approx {L_\theta }/( T/eZB{L_r}) $ its characteristic time scale, ![]() ${v_d} = T/( eZB{L_r}) $ the drift velocity with Lr a radial profile gradient length such as
${v_d} = T/( eZB{L_r}) $ the drift velocity with Lr a radial profile gradient length such as ![]() ${L_n} ={-} n/{{\bf \nabla }_r}n$ or
${L_n} ={-} n/{{\bf \nabla }_r}n$ or ![]() ${L_T} ={-} T/{{\bf \nabla }_r}T$. Here, Lθ is the poloidal scale length related to the poloidal mode number m as Lθ ≈ 2
${L_T} ={-} T/{{\bf \nabla }_r}T$. Here, Lθ is the poloidal scale length related to the poloidal mode number m as Lθ ≈ 2![]() ${\rm \pi}$a/m, where a is the plasma minor radius. This leads to
${\rm \pi}$a/m, where a is the plasma minor radius. This leads to ![]() $\chi \sim ( T/eZB) ( \Delta _r^2/{L_\theta }{L_r}) $ and gives rise to different scalings depending on the characteristic lengths scales assumed. Two such assumptions have proven particularly popular, providing fodder for three decades of debates over the nature of plasma turbulent transport. The first of these corresponds to ‘macro-turbulence’ and makes the assumption that all length scales are proportional to the plasma size itself (e.g. the minor radius) and leads to
$\chi \sim ( T/eZB) ( \Delta _r^2/{L_\theta }{L_r}) $ and gives rise to different scalings depending on the characteristic lengths scales assumed. Two such assumptions have proven particularly popular, providing fodder for three decades of debates over the nature of plasma turbulent transport. The first of these corresponds to ‘macro-turbulence’ and makes the assumption that all length scales are proportional to the plasma size itself (e.g. the minor radius) and leads to ![]() $\chi \propto T/eZB \propto {A^0}$. This diffusivity is called Bohm-like because has the same dependences as the classical Bohm diffusion coefficient (Bohm Reference Bohm, Guthrie and Wakerling1949; Spitzer Reference Spitzer1960). The Bohm diffusion coefficient is a worst case estimate obtained by assuming
$\chi \propto T/eZB \propto {A^0}$. This diffusivity is called Bohm-like because has the same dependences as the classical Bohm diffusion coefficient (Bohm Reference Bohm, Guthrie and Wakerling1949; Spitzer Reference Spitzer1960). The Bohm diffusion coefficient is a worst case estimate obtained by assuming ![]() ${\delta _t} = \omega _{\textrm{ci}}^{ - 1}$ and
${\delta _t} = \omega _{\textrm{ci}}^{ - 1}$ and ![]() ${\Delta _r} = {\rho _i}$. We wish to emphasise here that, despite their identical dependences on temperature and magnetic field, Bohm and Bohm-like diffusion belong to very different theoretical frameworks, the former making no reference to drifts, let alone drift waves and turbulence. GyroBohm scaling,
${\Delta _r} = {\rho _i}$. We wish to emphasise here that, despite their identical dependences on temperature and magnetic field, Bohm and Bohm-like diffusion belong to very different theoretical frameworks, the former making no reference to drifts, let alone drift waves and turbulence. GyroBohm scaling, ![]() $\chi \propto ( T/ZeB) ( {\rho _i}/R) \propto {A^{1/2}}$, follows from the assumptions
$\chi \propto ( T/ZeB) ( {\rho _i}/R) \propto {A^{1/2}}$, follows from the assumptions ![]() ${\Delta _r} \sim {\rho _i}$,
${\Delta _r} \sim {\rho _i}$, ![]() ${L_\theta } \sim {\rho _i}$ and
${L_\theta } \sim {\rho _i}$ and ![]() ${L_r} \sim a \propto R$, as expected for quasi-isotropic ion scale drift wave turbulence, i.e. ITG and trapped electron mode (TEM) turbulence. Equivalently, gyroBohm scaling can be obtained from a mixing length estimate,
${L_r} \sim a \propto R$, as expected for quasi-isotropic ion scale drift wave turbulence, i.e. ITG and trapped electron mode (TEM) turbulence. Equivalently, gyroBohm scaling can be obtained from a mixing length estimate, ![]() $\chi \approx \langle \gamma /k_ \bot ^2\rangle$, with
$\chi \approx \langle \gamma /k_ \bot ^2\rangle$, with ![]() ${k_ \bot } \propto 1/{\rho _i}$ and the growth rate
${k_ \bot } \propto 1/{\rho _i}$ and the growth rate ![]() $\gamma \propto {k_ \bot }{v_d}\,f( {L_{\textrm{Te}}}, \;{L_{\textrm{Ti}}}, \;{L_n}, \;{\nu _{\textrm{ei}}}, \;{T_i}/{T_e} \ldots ) $ if the complex dependencies in f are ignored (Horton, Choi & Tang Reference Horton, Choi and Tang1981; Waltz Reference Waltz1985; Horton Reference Horton1999; Bourdelle et al. Reference Bourdelle, Citrin, Baiocchi, Casati, Cottier, Garbet and Imbeaux2016).
$\gamma \propto {k_ \bot }{v_d}\,f( {L_{\textrm{Te}}}, \;{L_{\textrm{Ti}}}, \;{L_n}, \;{\nu _{\textrm{ei}}}, \;{T_i}/{T_e} \ldots ) $ if the complex dependencies in f are ignored (Horton, Choi & Tang Reference Horton, Choi and Tang1981; Waltz Reference Waltz1985; Horton Reference Horton1999; Bourdelle et al. Reference Bourdelle, Citrin, Baiocchi, Casati, Cottier, Garbet and Imbeaux2016).
Early experiments were at odds with gyroBohm scaling not only in the context of isotope dependencies: Experiments in DIII-D L-mode deuterium plasmas where species resolved transport investigations were performed showed ![]() ${\chi _i}\propto \rho _i^{ - 0.5}$ i.e. opposite in sign to gyroBohm, while the electron diffusivity scaled as
${\chi _i}\propto \rho _i^{ - 0.5}$ i.e. opposite in sign to gyroBohm, while the electron diffusivity scaled as ![]() ${\chi _e}\propto {\rho _e}$ (Petty et al. Reference Petty, Luce, Pinsker, Burrell, Chiu, Gohil, James and Wroblewski1995). GyroBohm scaling does remain the fundamental underlying scaling for both quasi-linear and nonlinear gyrokinetic physics in the local, electrostatic, collisionless, flowless limit with adiabatic electrons, as shown in nonlinear GYRO simulations (Pusztai, Candy & Gohil Reference Pusztai, Candy and Gohil2011). These have resulted in nonlinear heat fluxes that do indeed closely follow the expected scaling,
${\chi _e}\propto {\rho _e}$ (Petty et al. Reference Petty, Luce, Pinsker, Burrell, Chiu, Gohil, James and Wroblewski1995). GyroBohm scaling does remain the fundamental underlying scaling for both quasi-linear and nonlinear gyrokinetic physics in the local, electrostatic, collisionless, flowless limit with adiabatic electrons, as shown in nonlinear GYRO simulations (Pusztai, Candy & Gohil Reference Pusztai, Candy and Gohil2011). These have resulted in nonlinear heat fluxes that do indeed closely follow the expected scaling, ![]() $Q/Q_{\textrm{gB}}^\textrm{H}\propto {A^{ - 1/2}}$. The result is consistent with Rosenbluth–Hinton zonal flows (Rosenbluth & Hinton Reference Rosenbluth and Hinton1998), which have radial scales larger than the trapped ion widths and retain gyroBohm scaling of heat fluxes also in the nonlinear saturated stage. However, as seen in advanced modelling and in experiment, the above mentioned neglected physics can modify the basic gyroBohm scaling beyond recognition.
$Q/Q_{\textrm{gB}}^\textrm{H}\propto {A^{ - 1/2}}$. The result is consistent with Rosenbluth–Hinton zonal flows (Rosenbluth & Hinton Reference Rosenbluth and Hinton1998), which have radial scales larger than the trapped ion widths and retain gyroBohm scaling of heat fluxes also in the nonlinear saturated stage. However, as seen in advanced modelling and in experiment, the above mentioned neglected physics can modify the basic gyroBohm scaling beyond recognition.
The first mechanism discovered to be capable of causing deviations from gyroBohm scaling is most likely E × B shear flow stabilisation (Hahm & Burrell Reference Hahm and Burrell1995; Waltz et al. Reference Waltz, Dewar and Garbet1998). Such E × B shear flow may arise e.g. from sheared toroidal rotation due to momentum injection by NBH. It is also intrinsic to the formation of zonal flows (Rosenbluth & Hinton Reference Rosenbluth and Hinton1998; Diamond et al. Reference Diamond, Itoh, Itoh and Hahm2005; Hahm et al. Reference Hahm, Wang, Wang, Yoon and Duthoit2013; Bustos et al. Reference Bustos, Bañón Navarro, Görler, Jenko and Hidalgo2015) which damp/regulate the turbulence level in its developed, nonlinear state. The mechanism leads to turbulence quenching when the rotational flow shear rate exceeds the growth rate of the instability. It was not initially invoked for explaining isotope effects, however, we can see from a quasilinear estimate of ion heat diffusivity χi how an isotope dependence may arise from it. From ![]() $\gamma _{\textrm{max}}^i = \gamma _{\textrm{max}}^\textrm{H}{A^{ - 1/2}}$and hence
$\gamma _{\textrm{max}}^i = \gamma _{\textrm{max}}^\textrm{H}{A^{ - 1/2}}$and hence ![]() $\chi _{\textrm{gB}}^i = \chi _{\textrm{gB}}^i{A^{1/2}}$ it follows
$\chi _{\textrm{gB}}^i = \chi _{\textrm{gB}}^i{A^{1/2}}$ it follows
where ωE ×B is the shearing rate, which may arise from gradients of the toroidal velocity or from ion temperature gradients (see e.g. Ernst et al. Reference Ernst, Coppi, Scott and Porkolab1998), γ max is the growth rate of the fastest growing mode and α a parameter describing the strength of shear flow stabilisation. For ![]() $\alpha^\ast= \alpha \omega _{E \times B}/\gamma _{\textrm{max}}^\textrm{H} = 0$, there is no stabilisation, for
$\alpha^\ast= \alpha \omega _{E \times B}/\gamma _{\textrm{max}}^\textrm{H} = 0$, there is no stabilisation, for ![]() $\alpha^{\ast} \gt 0.36$,
$\alpha^{\ast} \gt 0.36$, ![]() ${\chi _\textrm{T}} \lt {\chi _\textrm{H}}$ as sketched in figure 1 and for
${\chi _\textrm{T}} \lt {\chi _\textrm{H}}$ as sketched in figure 1 and for ![]() $\alpha^{\ast} = 0.58$ there is complete suppression for tritium, but not for hydrogen and deuterium (where H, D and T stand for hydrogen, deuterium and tritium respectively). Hence the E × B effect may lead to an isotope effect opposite to gyroBohm both for E × B resulting from sheared bulk rotation and via zonal flows (Bustos et al. Reference Bustos, Bañón Navarro, Görler, Jenko and Hidalgo2015). It should hence be noted that deviations from gyroBohm scaling do not imply that the transport is not governed by ion scale turbulence (e.g. by macro-turbulence if a Bohm-like scaling,
$\alpha^{\ast} = 0.58$ there is complete suppression for tritium, but not for hydrogen and deuterium (where H, D and T stand for hydrogen, deuterium and tritium respectively). Hence the E × B effect may lead to an isotope effect opposite to gyroBohm both for E × B resulting from sheared bulk rotation and via zonal flows (Bustos et al. Reference Bustos, Bañón Navarro, Görler, Jenko and Hidalgo2015). It should hence be noted that deviations from gyroBohm scaling do not imply that the transport is not governed by ion scale turbulence (e.g. by macro-turbulence if a Bohm-like scaling, ![]() ${\chi _i}\propto {A^0}$, is observed). We also note that in ‘real world’ situations, the simple picture of (2.2) is likely to be complicated by the fact that ωE ×B itself, whether from zonal flows or externally imposed, is likely to also depend on the isotope mass.
${\chi _i}\propto {A^0}$, is observed). We also note that in ‘real world’ situations, the simple picture of (2.2) is likely to be complicated by the fact that ωE ×B itself, whether from zonal flows or externally imposed, is likely to also depend on the isotope mass.

Figure 1. Sketch to illustrate (2.2). Isotope dependence of shear flow stabilisation for 3 values of ![]() $\alpha^{\ast}= \alpha {\omega _{E \times B}}/{\gamma _{\max }}$, assuming gyroBohm scaling for underlying transport (α* = 0).
$\alpha^{\ast}= \alpha {\omega _{E \times B}}/{\gamma _{\max }}$, assuming gyroBohm scaling for underlying transport (α* = 0).
The E × B shear flow stabilisation was credited for stabilising turbulence in the H-mode edge transport barrier (Biglari Reference Biglari, Diamond and Terry1990; Hinton Reference Hinton1991) and in enhanced core confinement regimes such as the H-mode pedestal, VH (very high confinement) modes in DIII-D and TFTR supershots (Hahm & Burrell Reference Hahm and Burrell1996). In TFTR L-modes and supershots, E×B shearing was used to explain the not only improved confinement, but also the observation of stronger confinement improvement for D–T mixtures over pure D plasmas (Scott et al. Reference Scott, Zarnstorff, Barnes, Bell, Bretz, Bush, Chang, Ernst, Fonck and Johnson1995; Ernst et al. Reference Ernst, Coppi, Scott and Porkolab1998). However, with hindsight, other mechanisms, which were not yet discovered at the time, must have played a role too in these enhanced core confinement regimes.
Analytical work by Hahm et al. (Reference Hahm, Wang, Wang, Yoon and Duthoit2013) with kinetic particles showed that finer scale zonal flows (narrower than the ion banana width) can lead to reduced transport with respect to gyroBohm scaling for the heavier isotopes. This was confirmed in nonlinear simulations using the gyrokinetic code GENE (Jenko et al. Reference Jenko, Dorland, Kotschenreuther and Rogers2000; Görler et al. Reference Görler, Lapillonne, Brunner, Dannert, Jenko, Merz and Told2011), which exhibited notable deviations from gyroBohm scaling in TEM and mixed TEM/ITG turbulent plasmas with Ti/Te = 1, with ![]() ${Q^\textrm{T}}/Q_{\textrm{gB}}^\textrm{T}/( {Q^\textrm{H}}/Q_{\textrm{gB}}^\textrm{H}) \sim 0.82$ (Bustos et al. Reference Bustos, Bañón Navarro, Görler, Jenko and Hidalgo2015). The reduction of heat flux with isotope mass was attributed to a stronger zonal flow stabilisation of the turbulence at higher isotope mass, with ωE ×B/γ max increasing with isotope mass. A similar behaviour is observed when TEM turbulence is stabilised by electron–ion collisions: near marginality, the role of zonal flows in turbulence regulation is enhanced and this more strongly at high isotope mass (Nakata et al. Reference Nakata, Nunami, Sugama and Watanabe2017). This effects adds to the linear stabilisation of TEM by collisions which scales as
${Q^\textrm{T}}/Q_{\textrm{gB}}^\textrm{T}/( {Q^\textrm{H}}/Q_{\textrm{gB}}^\textrm{H}) \sim 0.82$ (Bustos et al. Reference Bustos, Bañón Navarro, Görler, Jenko and Hidalgo2015). The reduction of heat flux with isotope mass was attributed to a stronger zonal flow stabilisation of the turbulence at higher isotope mass, with ωE ×B/γ max increasing with isotope mass. A similar behaviour is observed when TEM turbulence is stabilised by electron–ion collisions: near marginality, the role of zonal flows in turbulence regulation is enhanced and this more strongly at high isotope mass (Nakata et al. Reference Nakata, Nunami, Sugama and Watanabe2017). This effects adds to the linear stabilisation of TEM by collisions which scales as ![]() ${v_{\textrm{eff}}}\sim {v_{\textrm{ei}}}/{\gamma _0}\propto {A^{1/2}}$, where γ 0 is the collisionless growth and is therefore stronger at high isotope mass (Angioni et al. Reference Angioni, Fable, Manas, Mantica and Schneider2018). Nonlinear GENE (Jenko et al. Reference Jenko, Dorland, Kotschenreuther and Rogers2000; Görler et al. Reference Görler, Lapillonne, Brunner, Dannert, Jenko, Merz and Told2011) simulations by one of the authors (M. Oberparleiter) in the course of the isotope effect investigations in JET (Maggi et al. Reference Maggi, Weisen, Hillesheim, Chankin, Delabie, Horvath, Auriemma, Carvalho, Corrigan and Flanagan2018; Weisen et al. Reference Weisen, Maggi, Menmuir, Horvath, Bache, Casson, Oberparleiter, Saarelma, Auriemma and Chankin2018) confirmed this mechanism is also active in ITG dominated turbulence and will be presented in detail later in the paper. A reversal of gyroBohm scaling has also been linked to the electron-to-ion mass ratio dependence of the non-adiabatic electron response when the turbulence is strongly influenced by the electron parallel dynamics (as for TEM and for the highly collisional plasma edge) (Belli, Candy & Waltz Reference Belli, Candy and Waltz2019; Bonanomi et al. Reference Bonanomi, Angioni, Crandall, Di Siena, Maggi and Schneider2019a).
${v_{\textrm{eff}}}\sim {v_{\textrm{ei}}}/{\gamma _0}\propto {A^{1/2}}$, where γ 0 is the collisionless growth and is therefore stronger at high isotope mass (Angioni et al. Reference Angioni, Fable, Manas, Mantica and Schneider2018). Nonlinear GENE (Jenko et al. Reference Jenko, Dorland, Kotschenreuther and Rogers2000; Görler et al. Reference Görler, Lapillonne, Brunner, Dannert, Jenko, Merz and Told2011) simulations by one of the authors (M. Oberparleiter) in the course of the isotope effect investigations in JET (Maggi et al. Reference Maggi, Weisen, Hillesheim, Chankin, Delabie, Horvath, Auriemma, Carvalho, Corrigan and Flanagan2018; Weisen et al. Reference Weisen, Maggi, Menmuir, Horvath, Bache, Casson, Oberparleiter, Saarelma, Auriemma and Chankin2018) confirmed this mechanism is also active in ITG dominated turbulence and will be presented in detail later in the paper. A reversal of gyroBohm scaling has also been linked to the electron-to-ion mass ratio dependence of the non-adiabatic electron response when the turbulence is strongly influenced by the electron parallel dynamics (as for TEM and for the highly collisional plasma edge) (Belli, Candy & Waltz Reference Belli, Candy and Waltz2019; Bonanomi et al. Reference Bonanomi, Angioni, Crandall, Di Siena, Maggi and Schneider2019a).
Electromagnetic effects can lead to an isotope effect as well through a nonlinear process as demonstrated for an ITER case in DD vs DT. Whereas linear simulations do not show a departure from gyroBohm scaling, at high beta the ion heat flux decreases with increasing mass due to a nonlinear interplay between zonal flows, electromagnetic effects and mass (Garcia et al. Reference Garcia, Görler, Jenko and Giruzzi2017). Such a deviation from gyroBohm scaling is enhanced in plasma conditions of high beta and high E × B shearing, as expected in advanced tokamak scenarios with high NBH power. In the particular case of DD vs DT plasmas, the additional fast ion contribution from the alpha particles from DT reactions can further reduce the ion heat flux by fast ion electromagnetic stabilisation resulting in considerable de-stiffening of the ITG mode, typically halving the ion heat flux for a given ion temperature gradient length (Garcia et al. Reference Garcia, Görler and Jenko2018). The higher fast ion pressure in deuterium plasmas heated by energetic ions has led to improved core confinement in a set of L-mode experiments in JET, with 3He minority ion cyclotron resonance heating (ICRH) in addition to NBH (Bonanomi et al. Reference Bonanomi, Casiraghi, Mantica, Challis, Delabie, Fable, Gallar, Giroud, Lerche and Lomas2019b). It is important to stress that a different fast ion contribution in different plasma species is not an inherent isotope effect. In the case of a comparison of D and DT plasmas such an effect, if not understood, may lead to erroneously attributing the improved confinement in DT to a mass dependence.
Modelling of transport in the edge plasma and pedestal is still in its infancy, but deserves particular attention, as it sets the boundary conditions and via profile stiffness influences and often largely determines global confinement (Bateman et al. Reference Bateman, Kritz, Parail and Cordey1999). Strong ion mass effects have been obtained in electromagnetic gyrokinetic GENE simulations of L-mode edges in AUG and JET (Bonanomi et al. Reference Bonanomi, Angioni, Crandall, Di Siena, Maggi and Schneider2019b). The results show that edge turbulence is radically distinct from core turbulence. Electron parallel dynamics is important due to the high collisionalities at the edge, leading, in linear electrostatic simulations, to a stronger non-adiabatic electron response at low ion mass and to a lower R/L Te threshold for hydrogen than for deuterium. This linear effect is also seen in nonlinear simulations, resulting in a strong deviation from gyroBohm ![]() $( {\chi _\textrm{H}}\sim 2{\chi _\textrm{D}}) $ already in electrostatic simulations. Due to the steep gradients, electromagnetic effects are also important despite the relatively low local thermal β. MHD-like electron drift waves are strongly destabilised even at low (with respect to core values) values of βe. This destabilisation especially affects modes with low wave numbers and is found to take place below the threshold in βe expected from linear simulations (Bonanomi et al. Reference Bonanomi, Angioni, Crandall, Di Siena, Maggi and Schneider2019b). This behaviour puts into question the applicability in the edge plasma of the conventional approach of developing quasilinear models for describing transport. These novel results on the L-mode edge call for an extension of gyrokinetic modelling to the H-mode pedestal, which is found to be responsible for most of the isotope scaling of confinement observed in JET H-modes, as reported in § 5.
$( {\chi _\textrm{H}}\sim 2{\chi _\textrm{D}}) $ already in electrostatic simulations. Due to the steep gradients, electromagnetic effects are also important despite the relatively low local thermal β. MHD-like electron drift waves are strongly destabilised even at low (with respect to core values) values of βe. This destabilisation especially affects modes with low wave numbers and is found to take place below the threshold in βe expected from linear simulations (Bonanomi et al. Reference Bonanomi, Angioni, Crandall, Di Siena, Maggi and Schneider2019b). This behaviour puts into question the applicability in the edge plasma of the conventional approach of developing quasilinear models for describing transport. These novel results on the L-mode edge call for an extension of gyrokinetic modelling to the H-mode pedestal, which is found to be responsible for most of the isotope scaling of confinement observed in JET H-modes, as reported in § 5.
2.2. Operational effects
It is difficult, and often impossible, to perform experiments in which an isotope is substituted for another, without changing any other plasma parameters. These operational effects can obscure the intrinsic transport effects, making their unambiguous identification difficult. Neutral beam heating and ICRH confer heat to electrons and ions in proportions which depend on the background ion as well as on the fast particle masses and energies. Moreover, no ICRH method can be applied indistinctly to plasmas with arbitrary isotopes or isotope mixtures. The power, torque and particle sources by NBH depend on both beam ion isotopes and hence also on the background plasma, as the general preference is to use the same species for NBH as for the main plasma. This warning can be extended to a comparison of D and DT plasmas, as the latter, unlike the former, will produce alpha particles which are potentially capable of reducing ITG turbulence by electromagnetic effects (Garcia, Görler & Jenko Reference Garcia, Görler and Jenko2018).
Equipartional energy exchange between ions and electrons, as well as between ions, depends on the plasma isotopes, affecting the ion and electron power balances and hence transport. Such a case was reported from a comparison of ECH heated L-mode in hydrogen and deuterium in ASDEX-upgrade (Schneider et al. Reference Schneider, Bustos, Hennequin, Ryter, Bernert, Cavedon, Dunne, Fischer, Görler and Happel2017). The two discharges achieved the same electron temperature profiles and nearly the same ion temperature profiles, although the hydrogen discharge required 1.4 MW of ECH power for only 1.06 MW for the deuterium discharge. A species resolved power balance calculation revealed that the electron heat flux was unchanged, however the ion heat flux was 1.5–2 times larger due to stronger electrons–ion thermal equipartition for the hydrogen case. The additional heat flux had virtually no effect in the ion temperature profile because of profiles stiffness as modelled using a critical gradient model (Garbet et al. Reference Garbet, Mantica, Ryter, Cordey, Imbeaux, Sozzi, Manini, Asp, Parail and Wolf2004). In JET ohmic discharges too, the difference in electron–ion equipartition between hydrogen and deuterium was found to be a key parameter in understanding the observed somewhat larger ion heat diffusivity in hydrogen (Delabie et al. Reference Delabie, Nave, Baruzzo, Bernardo, Boom, Buchanan, Hawkes, Hillesheim, Maggi and Menmuir2017).
The edge neutral penetration is deeper for the lighter species, which is expected to help fuelling for the lighter species. Cryopumping is more effective for the heavier hydrogenic species, affecting divertor and edge conditions. Orbit losses are reduced for the lighter species. Some effects are not understood, as for instance the cause of the much higher particle transport in the edge of hydrogen H-modes in JET-ILW (Maggi et al. Reference Maggi, Weisen, Hillesheim, Chankin, Delabie, Horvath, Auriemma, Carvalho, Corrigan and Flanagan2018) and ASDEX-upgrade (Laggner et al. Reference Laggner, Wolfrum, Cavedon, Mink, Bernert, Dunne, Schneider, Kappatou, Birkenmeier and Fischer2017) (but not in JT-60U Urano et al. (Reference Urano, Takizuka, Aiba, Kikuchi, Nakano, Fujita, Oyama, Kamada and Hayashi2013)), which affect overall confinement. The planned DT experiments in JET have prompted a multi-campaign investigation of isotope effects in view of understanding the physics and in order to provide better extrapolation to the performance to be expected from the discharges under preparation for DT. Many of the results in hydrogen and deuterium plasmas have already been reported and will not be repeated here (Maggi et al. Reference Maggi, Weisen, Hillesheim, Chankin, Delabie, Horvath, Auriemma, Carvalho, Corrigan and Flanagan2018, Reference Maggi, Weisen, Casson, Auriemma, Lorenzini, Nordman, Delabie, Eriksson, Flanagan and Keeling2019).
3. Diagnostics and data analysis for JET-ILW isotope studies
The most important diagnostics used in this study were the two Thomson scattering systems, HRTS (Frasinetti et al. Reference Frasinetti, Beurskens, Scannell, Osborne, Flanagan, Kempenaars, Maslov, Pasqualotto and Walsh2012) and LIDAR (Maslov et al. Reference Maslov, Beurskens, Kempenaars and Flanagan2013) for electron temperature and density profiles. Unless otherwise indicated, we have used the HRTS system because of its better spatial resolution. Charge exchange spectroscopy (CXS) data for Ti and toroidal angular frequency ωϕ are available for about half of the dataset (Giroud et al. Reference Giroud, Meigs, Negus, Zastrow, Biewer and Versloot2008). Uncertainties on Ti derived from CXS on impurity lines are significantly higher in JET-ILW due to reduced carbon levels and the appearance of multiple tungsten ‘nuisance’ lines, than they were in JET-C. The electron temperatures in these discharges were also generally too low for reliable ion temperature measurements using X-ray crystal spectrometry for the a 59Ni26+ K-shell at X-ray line at 1.6 Å (Shumack et al. Reference Shumack, Rzadkiewicz, Chernyshova, Jakubowska, Scholz, Byszuk, Cieszewski, Czarski, Dominik and Karpinski2014). Consequently, all profile data were subjected to a thermal ‘equipartition test’ in order to filter out any data points (~12 % of cases) where the calculated ion-to-electron equipartition power p ie (which is proportional to Ti − Te) integrated over the volume ![]() ${Q_{\textrm{ie}}} = \int {{p_{\textrm{ie}}}\,\textrm{d}V}$ exceeded the integrated deposited ion source power
${Q_{\textrm{ie}}} = \int {{p_{\textrm{ie}}}\,\textrm{d}V}$ exceeded the integrated deposited ion source power ![]() ${Q_{\textrm{is}}} = \int {{p_{\textrm{is}}}\,\textrm{d}V}$. A useful way of testing equipartition is to compare the measured ion temperatures to a set fictional ion temperature profiles, dubbed ‘equipartition ion temperatures’, consistent with a certain fraction fi of the source power being transferred to the electrons by equipartition (Weisen et al. Reference Weisen, Delabie, Flanagan, Giroud, Maslov, Menmuir, Patel, Scott, Siren and Varje2020). In other words, Ti(fi,ρ) refers to the ion temperature profile required to have that Q ie = fi × Q is and is calculated on the basis of the measured electron density and temperature profiles and the ion heat deposition profile. The relevant temperature profiles are shown for one example in figure 2, for fi = 0.2, 0.5 and 1. For illustration purposes, we have chosen a sample with one of the highest measured ratios of Ti/Te. An analogous power balance can be calculated for electrons (fe-labelled profiles in figure 2, although not relevant to this case), if net equipartition is from the electrons to the ions.
${Q_{\textrm{is}}} = \int {{p_{\textrm{is}}}\,\textrm{d}V}$. A useful way of testing equipartition is to compare the measured ion temperatures to a set fictional ion temperature profiles, dubbed ‘equipartition ion temperatures’, consistent with a certain fraction fi of the source power being transferred to the electrons by equipartition (Weisen et al. Reference Weisen, Delabie, Flanagan, Giroud, Maslov, Menmuir, Patel, Scott, Siren and Varje2020). In other words, Ti(fi,ρ) refers to the ion temperature profile required to have that Q ie = fi × Q is and is calculated on the basis of the measured electron density and temperature profiles and the ion heat deposition profile. The relevant temperature profiles are shown for one example in figure 2, for fi = 0.2, 0.5 and 1. For illustration purposes, we have chosen a sample with one of the highest measured ratios of Ti/Te. An analogous power balance can be calculated for electrons (fe-labelled profiles in figure 2, although not relevant to this case), if net equipartition is from the electrons to the ions.

Figure 2. Profiles from hydrogen pulse 92232: Electron temperature Te (blue), the measured impurity temperatures from the main CXS system (black sybols) and the edge CXS system (magenta symbols at ρ pol > 0.8). The broken green, orange and red lines labelled fi and fe are ‘equipartition ion temperatures’ and are explained in the main text.
Clearly fi ≥ 1 is unphysical, as the ions would have zero or negative net heat flux. Figure 2 also shows the CXS impurity temperatures simultaneously inferred from Ne and C in black, the former having been introduced as a tracer (with n Ne/ne ~ 0.2 %) to improve the measurements. With collisional ion heating, as here with NBH, the main ion temperatures T main can can be somewhat lower than the impurity temperature (Weisen et al. Reference Weisen, Delabie, Flanagan, Giroud, Maslov, Menmuir, Patel, Scott, Siren and Varje2020). In the majority of cases in this dataset (T imp − T main)/T main < 0.03 in the plasma core and (T imp − T main)/T main < 0.01 near the plasma boundary and is insignificant for this study.
The fact the T imp profile in figure 2 is close to the ‘equipartition ion temperature’ calculated for fi = 0.2 is not a coincidence (Weisen et al. Reference Weisen, Maggi, Menmuir, Horvath, Bache, Casson, Oberparleiter, Saarelma, Auriemma and Chankin2018, Reference Weisen, Delabie, Flanagan, Giroud, Maslov, Menmuir, Patel, Scott, Siren and Varje2020) and is used to improve on the assumption Ti = Te. When the JET isotope experiments were first analysed (Maggi et al. Reference Maggi, Weisen, Hillesheim, Chankin, Delabie, Horvath, Auriemma, Carvalho, Corrigan and Flanagan2018), ion temperature measurements were not available and Ti = Te had to be assumed. For this paper, ion temperatures from CXS for approximately half the discharges presented became later available. The power balance analysis allows this assumption to be replaced by the assumption ![]() ${T_{\textrm{main}}}( \rho ) = {T_{\textrm{ieq}}}(\,{f_i} = 0.2, \;\rho ) $, i.e. by adopting
${T_{\textrm{main}}}( \rho ) = {T_{\textrm{ieq}}}(\,{f_i} = 0.2, \;\rho ) $, i.e. by adopting ![]() ${T_{\textrm{ieq}}}(\,{f_i} = 0.2, \;\rho ) $ as a proxy for T main for the purpose of improved confinement regressions, using the complete experimental dataset. The data analysis for the global confinement in JET discharges presented in §§ 4 and 5 was performed using the JETPEAK database, presented in appendix 1 of Weisen et al. (Reference Weisen, Delabie, Flanagan, Giroud, Maslov, Menmuir, Patel, Scott, Siren and Varje2020).
${T_{\textrm{ieq}}}(\,{f_i} = 0.2, \;\rho ) $ as a proxy for T main for the purpose of improved confinement regressions, using the complete experimental dataset. The data analysis for the global confinement in JET discharges presented in §§ 4 and 5 was performed using the JETPEAK database, presented in appendix 1 of Weisen et al. (Reference Weisen, Delabie, Flanagan, Giroud, Maslov, Menmuir, Patel, Scott, Siren and Varje2020).
Isotope ratios were primarily based on line intensity ratios from high resolution Balmer-alpha spectroscopy, using a set of several vertical viewing lines passing through the divertor (Neverov et al. Reference Neverov, Kukushkin, Stamp, Alekseev, Brezinsek and von Hellermann2017). Residual gas analysis in the sub-divertor, based on Penning gauge spectroscopy (Kruezi et al. Reference Kruezi, Sergienko, Morgan, Matthews, Brezinsek and Vartanian2012) was also available. These isotope fractions n D/(n D + n H) and n H/(n D + n H) from the two diagnostics were found to agree within a few per cent. The majority of the JET results presented here are in ‘pure’ isotope plasmas, i.e. the external gas fuelling and the NBH used the same isotope. In these conditions the purity of that isotope was typically better than 97 %. In mixed H/D plasmas the core isotope composition was inferred from the measured DD neutron rates as explained in § 5.4 and in Maslov et al. (Reference Maslov, King, Viezzer, Keeling, Giroud, Tala, Salmi, Marin, Citrin and Bourdelle2018), King et al. (Reference King, Viezzer, Baruzzo, Belonohy, Buchanan, Carvalho, Cave-Ayland, Coffey, Challis and Delabie2017, Reference King, Viezzer, Balboa, Baruzzo, Belonohy, Buchanan, Carvalho, Cave-Ayland, Coffey and Challis2020).
4. Isotope dependence of global confinement in JET-ILW L-modes
A dataset of 20 samples was obtained by NBH power scans in hydrogen and deuterium with B T = 3 T, Ip = 2.5 MA, ![]() $\langle {n_e}\rangle \cong 3.1 \times {10^{19}}\;{\textrm{m}^{ - 3}}$, 1.5 MW ≤ P NBI ≤ 9.5 MW, B T is the toroidal magnetic field at the vessel centre, Ip the plasma current, P NBI the NBH power and
$\langle {n_e}\rangle \cong 3.1 \times {10^{19}}\;{\textrm{m}^{ - 3}}$, 1.5 MW ≤ P NBI ≤ 9.5 MW, B T is the toroidal magnetic field at the vessel centre, Ip the plasma current, P NBI the NBH power and ![]() $\langle {n_e}\rangle $ is the volume averaged density. The experiment was intended to be carried out at constant density, however, this was successful only within ±10 %. The divertor strike points were placed on the vertical tiles for highest H-mode power threshold in order to maximise the L-mode domain in these experiments. It was previously shown that these discharges are dominated by ITG turbulence (Maggi et al. Reference Maggi, Weisen, Hillesheim, Chankin, Delabie, Horvath, Auriemma, Carvalho, Corrigan and Flanagan2018).
$\langle {n_e}\rangle $ is the volume averaged density. The experiment was intended to be carried out at constant density, however, this was successful only within ±10 %. The divertor strike points were placed on the vertical tiles for highest H-mode power threshold in order to maximise the L-mode domain in these experiments. It was previously shown that these discharges are dominated by ITG turbulence (Maggi et al. Reference Maggi, Weisen, Hillesheim, Chankin, Delabie, Horvath, Auriemma, Carvalho, Corrigan and Flanagan2018).
The thermal stored energy is calculated as
where ni is estimated as
The electron density in JET L-modes is easily controlled via the gas puff rate. JET-ILW plasmas are of high purity with the bulk of the data presented having 1.05 < Z eff < 1.6, as inferred from visible bremsstrahlung measurements for this L-mode dataset. As a result, errors on ni/ne inferred by assuming a single impurity species are small (<10 %). Figure 3 shows a regression for the thermal stored energy assuming ![]() ${T_i}( \rho ) = {T_{\textrm{ieq}}}(\,{f_i} = 0.2, \;\rho ) $:
${T_i}( \rho ) = {T_{\textrm{ieq}}}(\,{f_i} = 0.2, \;\rho ) $:
where P is the total deposited power.

Figure 3. Regression of thermal stored energy expressed in MJ in L-mode dataset as in (4.3). P tot is the total power, A is the isotope mass, ![]() $\langle {n_e}\rangle $ the volume average density and σ the standard deviation. The legend is explained in the main text.
$\langle {n_e}\rangle $ the volume average density and σ the standard deviation. The legend is explained in the main text.
The lower legend of the figure shows, from left to right, the standard deviation σ of the regression, the variable names, the fit coefficients (b, the exponents of the power law), their errors for a 10 % confidence interval (δb), the statistical significance (b/δb) and the normalised statistical relevance (STR), which for every regressor i is given by bi ⋅ σi/σt where σi is the standard deviation for regressor i in the dataset and σt is the standard deviation of the target variable (Kardaun Reference Kardaun2005). Hence the STR quantifies to what extent a particular regressor contributes to the variations of the target variable.
The uncertainties in the measured density and temperature profiles are typically of order 10 %. Assuming ![]() ${T_i}( \rho ) = {T_{\textrm{ieq}}}(\,{f_i} = 0.2, \;\rho ) $, the core ion temperatures exceed the electron temperatures by 3 % (at P NBI = 3 MW) to 8 % (for P NBI = 9 MW) in deuterium and by 1 % (at P NBI = 3 MW) to 5 % (for P NBI = 9 MW) in hydrogen. A comprehensive study (Weisen et al. Reference Weisen, Delabie, Flanagan, Giroud, Maslov, Menmuir, Patel, Scott, Siren and Varje2020) shows that for those cases where Ti is available from CXS, fi > 0.4 is very rare and the few such cases observed may well be the result of measurement errors. Hence, we consider a core a core ion temperature exceeding the electron temperature by 16 % as the upper error bar for P NBI = 9 MW. Moreover, the relative difference between T ieq(fi, ρ)) and Te becomes very small (a few %) near the LCFS, which contributes significantly to W th to due to the large volume. Altogether, the usage of T ieq(fi = 0.2, ρ) in (4.1) brings an improvement over the assumption Ti = Te, albeit admittedly, a modest one. Z eff in these low power discharges is near 1.15 for P ≈ 3 MW, rising to between 1.2 and 1.45 for P ≈ 9 MW, with an error estimated from the data dispersion to ~0.1. This corresponds to an error in ni = n D + n H + n Be of less than 3 %, which therefore contributes little to the overall errors on W th. Finally we should note that the errors on W th propagate only partly to the scaling exponents, as systematic over- and underestimates by constant factors, which are most difficult to quantify, have no effect on the scaling exponents.
${T_i}( \rho ) = {T_{\textrm{ieq}}}(\,{f_i} = 0.2, \;\rho ) $, the core ion temperatures exceed the electron temperatures by 3 % (at P NBI = 3 MW) to 8 % (for P NBI = 9 MW) in deuterium and by 1 % (at P NBI = 3 MW) to 5 % (for P NBI = 9 MW) in hydrogen. A comprehensive study (Weisen et al. Reference Weisen, Delabie, Flanagan, Giroud, Maslov, Menmuir, Patel, Scott, Siren and Varje2020) shows that for those cases where Ti is available from CXS, fi > 0.4 is very rare and the few such cases observed may well be the result of measurement errors. Hence, we consider a core a core ion temperature exceeding the electron temperature by 16 % as the upper error bar for P NBI = 9 MW. Moreover, the relative difference between T ieq(fi, ρ)) and Te becomes very small (a few %) near the LCFS, which contributes significantly to W th to due to the large volume. Altogether, the usage of T ieq(fi = 0.2, ρ) in (4.1) brings an improvement over the assumption Ti = Te, albeit admittedly, a modest one. Z eff in these low power discharges is near 1.15 for P ≈ 3 MW, rising to between 1.2 and 1.45 for P ≈ 9 MW, with an error estimated from the data dispersion to ~0.1. This corresponds to an error in ni = n D + n H + n Be of less than 3 %, which therefore contributes little to the overall errors on W th. Finally we should note that the errors on W th propagate only partly to the scaling exponents, as systematic over- and underestimates by constant factors, which are most difficult to quantify, have no effect on the scaling exponents.
The inferred difference in Ti/Te between high and low power plasmas indicates that stronger electron–ion equipartition, as in Schneider et al. (Reference Schneider, Bustos, Hennequin, Ryter, Bernert, Cavedon, Dunne, Fischer, Görler and Happel2017) and the stronger direct electron heating by NBH play a role in the scaling. If we simply assume Ti = Te the mass scaling is slightly weaker:
If the thermal energy is inferred from the plasma energy Wp provided by unconstrained EFIT (General Atomics) equilibrium reconstruction and the perpendicular and parallel fast particle contributions ![]() ${W_{f \bot }}$ and Wf // as
${W_{f \bot }}$ and Wf // as
the mass exponent is regressed as
Here, Wf // and ![]() ${W_{f \bot }}$ used in (4.4) are the parallel and perpendicular fast particle stored energies and were obtained from the PENCIL (Challis et al. Reference Challis, Cordey, Hamnen, Stubberfield, Christiansen, Lazzaro, Muir, Stork and Thompson1989) NBH code. Equation (4.5) can be inferred from the effect of pressure anisotropy on the equilibrium (Cooper & Wootton Reference Cooper and Wootton1982; Fitzgerald, Hole & Qu Reference Fitzgerald, Hole and Qu2015). In all of the above regressions, the mass exponents are close to the L-mode exponents published the ITER Physics Basis (Kaye et al. Reference Kaye, Greenwald, Stroth, Kardaun, Kus, Schissel, DeBoo, Bracco, Thomsen and Cordey1997) and to the one previously reported for JET-ILW (Maggi et al. Reference Maggi, Weisen, Hillesheim, Chankin, Delabie, Horvath, Auriemma, Carvalho, Corrigan and Flanagan2018).
${W_{f \bot }}$ used in (4.4) are the parallel and perpendicular fast particle stored energies and were obtained from the PENCIL (Challis et al. Reference Challis, Cordey, Hamnen, Stubberfield, Christiansen, Lazzaro, Muir, Stork and Thompson1989) NBH code. Equation (4.5) can be inferred from the effect of pressure anisotropy on the equilibrium (Cooper & Wootton Reference Cooper and Wootton1982; Fitzgerald, Hole & Qu Reference Fitzgerald, Hole and Qu2015). In all of the above regressions, the mass exponents are close to the L-mode exponents published the ITER Physics Basis (Kaye et al. Reference Kaye, Greenwald, Stroth, Kardaun, Kus, Schissel, DeBoo, Bracco, Thomsen and Cordey1997) and to the one previously reported for JET-ILW (Maggi et al. Reference Maggi, Weisen, Hillesheim, Chankin, Delabie, Horvath, Auriemma, Carvalho, Corrigan and Flanagan2018).
The difference in exponents for P and ![]() $\langle {n_e}\rangle $ between (4.6) and (4.4) is likely due to it being poorly constrained due to the smallness of the variations of
$\langle {n_e}\rangle $ between (4.6) and (4.4) is likely due to it being poorly constrained due to the smallness of the variations of ![]() $\langle {n_e}\rangle $ (±10 %). Because of the limited variations in
$\langle {n_e}\rangle $ (±10 %). Because of the limited variations in ![]() $\langle {n_e}\rangle $, the density exponents are not significant. Although the density dependence is not the subject of this study, it raises the question whether the weak mass dependence itself may be biased by the small variations in density in the dataset and the correlation between density and isotope mass. The correlation coefficients between these parameters is +0.39, which is not negligible. We therefore have repeated the above regressions ((4.3), (4.4), (4.6)) leaving out the density with the results
$\langle {n_e}\rangle $, the density exponents are not significant. Although the density dependence is not the subject of this study, it raises the question whether the weak mass dependence itself may be biased by the small variations in density in the dataset and the correlation between density and isotope mass. The correlation coefficients between these parameters is +0.39, which is not negligible. We therefore have repeated the above regressions ((4.3), (4.4), (4.6)) leaving out the density with the results ![]() ${W_{\textrm{th}}}\propto {P^{0.39 \pm 0.05}}{A^{0.23 \pm 0.05}}$,
${W_{\textrm{th}}}\propto {P^{0.39 \pm 0.05}}{A^{0.23 \pm 0.05}}$, ![]() ${W_{\textrm{th2}}}\propto {P^{0.36 \pm 0.05}}{A^{0.2 \pm 0.05}}$ and
${W_{\textrm{th2}}}\propto {P^{0.36 \pm 0.05}}{A^{0.2 \pm 0.05}}$ and ![]() ${W_{\textrm{thMHD}}}\propto {P^{0.5 \pm 0.03}}{A^{0.17 \pm 0.03}}$. We note that, as expected, the exponents for A are now higher, but only slightly so, as the isotope dependence so obtained incorporates both the intrinsic isotope dependence and the effect of the correlation with the density. The mass exponents obtained without taking into account the density variations should therefore be considered as upper limits. We conclude that the (unwanted) density variations in the dataset do not alter our conclusion and that the isotope dependence for energy confinement in L-mode is weak, with a mass exponent estimated to be in the range 0.14–0.18, as indicated by regressions (4.3), (4.4) and (4.6).
${W_{\textrm{thMHD}}}\propto {P^{0.5 \pm 0.03}}{A^{0.17 \pm 0.03}}$. We note that, as expected, the exponents for A are now higher, but only slightly so, as the isotope dependence so obtained incorporates both the intrinsic isotope dependence and the effect of the correlation with the density. The mass exponents obtained without taking into account the density variations should therefore be considered as upper limits. We conclude that the (unwanted) density variations in the dataset do not alter our conclusion and that the isotope dependence for energy confinement in L-mode is weak, with a mass exponent estimated to be in the range 0.14–0.18, as indicated by regressions (4.3), (4.4) and (4.6).
The total particle content ![]() ${N_e} = \int {{n_e}\,\textrm{d}V}$ is best regressed with A and a proxy for the edge particle source Γ given by the Balmer-alpha emission measured along a horizontal line in the vessel midplane, as seen in figure 4.
${N_e} = \int {{n_e}\,\textrm{d}V}$ is best regressed with A and a proxy for the edge particle source Γ given by the Balmer-alpha emission measured along a horizontal line in the vessel midplane, as seen in figure 4.
While the density variations in the dataset are small (±10 %), the regressions are constrained by the variations of isotope mass (factor 2) and of Γ (factor 3). The observation that the energy and the particle confinement have similar isotope scaling, within errors, is unlikely to be a result of chance, as turbulent transport theory generally predict a close relationship (Bourdelle et al. Reference Bourdelle, Bourdelle, Camenen, Citrin, Marin, Casson, Koechl and Maslov2018). A hydrogen/deuterium pair from the above set with nearly the same thermal stored energy (1.2 MJ) and line averaged density (3.1 × 1019 m−3) with respectively 4.4 MW (hydrogen) and 3.2 MW (deuterium) NBH, was predictively modelled under conditions of imposed heat flux using JETTO with the TGLF SAT-1 quasilinear transport model, which is based on nonlinear turbulence simulations based on the GYRO code (Staebler, Waltz & Kinsey Reference Staebler, Waltz and Kinsey2007; Staebler et al.Reference Staebler, Howard, Candy and Holland2017). We must note here that this version of TGLF is based on simulations in deuterium only. The boundary conditions, imposed at ρ = 0.85, were taken from the experimental data. Predicted and experimental profiles, shown in figure 5, are in good agreement for deuterium, less so for hydrogen, for which temperature and density are overpredicted (Garcia et al. Reference Garcia, Dumont, Joly, Morales, Garzotti, Bache, Baranov, Casson, Challis and Kirov2019). ITG modes are dominant in the core and the inclusion of E × B shear from NBH driven toroidal rotation in these cases does not lead to an improvement of deuterium confinement relative to hydrogen. We note, however, from the available CXS data, that the toroidal rotation and its shear in hydrogen were 10%–30 % larger in hydrogen than in deuterium. The predictions yield nearly the same global confinement time for both species (τE, pred = 0.294 for hydrogen, 0.283 for deuterium), i.e. neither gyroBohm scaling, nor weak anti-gyroBohm scaling, as indicated by the experimental results. This is interpreted as resulting from profile stiffness (high resilience of R/LT to changes in the heat flux) which is seen in the experiment (Maggi et al. Reference Maggi, Weisen, Hillesheim, Chankin, Delabie, Horvath, Auriemma, Carvalho, Corrigan and Flanagan2018) and is borne out in the simulations. Results may change in future versions of TGLF trained on both deuterium and hydrogen, although they would still remain constrained by the boundary conditions.

Figure 5. Experimental (dashed lines) and simulated (continuous lines) profiles for hydrogen (blue) and deuterium (red) L-mode discharges with the same stored energy. Hydrogen: #91450, P = 4.4 MW,τE ,exp = 0.235 s, τE ,pred = 0.294 s. Deuterium: #89723, P = 3.2 MW, τE ,exp = 0.283 s, τE ,pred = 0.289 s.
These experiments were also modelled using the gyrokinetic code GENE (Jenko et al. Reference Jenko, Dorland, Kotschenreuther and Rogers2000; Görler et al. Reference Görler, Lapillonne, Brunner, Dannert, Jenko, Merz and Told2011). The simulations have shown that the E × B shearing rate, the effects of collisions and of trapped electrons lead to deviations from the expected gyroBohm scaling in ITG dominated plasmas (Garcia et al. Reference Garcia, Dumont, Joly, Morales, Garzotti, Bache, Baranov, Casson, Challis and Kirov2019). Analyses were also performed for the above L-mode discharge #91450 (hydrogen) by artificially changing the mass from 1 to 2 (Garcia et al. Reference Garcia, Dumont, Joly, Morales, Garzotti, Bache, Baranov, Casson, Challis and Kirov2019). With the above effects included, the ratio Q D/Q H is ~0.85. However, Q D/Q H progressively increases by removing these effects one by one, recovering gyroBohm scaling (Q D/Q H = √2) when all are removed. E × B shearing and the effect of collisions are found to be the largest contributors to the deviations from gyroBohm scaling.
In a separate experiment, a H/D pair of L-mode discharges matched for being identical in the dimensionless parameters ρ*, β, ν* and q, was created (Maggi et al. Reference Maggi, Weisen, Casson, Auriemma, Lorenzini, Nordman, Delabie, Eriksson, Flanagan and Keeling2019). This was achieved at IP/B = 2.5 MA/3.0 T in D and 1.48 MA/1.78 T in H, q 95 = 3.4, δ = 0.2, with strike points on divertor vertical targets. In order to keep the ρ*, β, ν* and q profiles fixed when varying the isotope mass, the plasma parameters must be scaled as IP, ![]() ${B_\textrm{T}}\propto {A^{3/4}}$; n ∝ A and T ∝ A 1/2 (Cordey et al. Reference Cordey, Alper, Budny, Christiansen, Coffey, Erents, Harbour, Horton, Lawson and Matthews2000). The experiments achieved scale invariance, i.e. the normalised profiles were identical. The same scale invariance principle also predicts that
${B_\textrm{T}}\propto {A^{3/4}}$; n ∝ A and T ∝ A 1/2 (Cordey et al. Reference Cordey, Alper, Budny, Christiansen, Coffey, Erents, Harbour, Horton, Lawson and Matthews2000). The experiments achieved scale invariance, i.e. the normalised profiles were identical. The same scale invariance principle also predicts that ![]() ${\omega _{\textrm{ci}}}{\tau _{\textrm{Eth}}}\propto B{\tau _{\textrm{Eth}}}/A$ is invariant under this scale invariant transformation. In these experiments
${\omega _{\textrm{ci}}}{\tau _{\textrm{Eth}}}\propto B{\tau _{\textrm{Eth}}}/A$ is invariant under this scale invariant transformation. In these experiments ![]() $B{\tau _{\textrm{Eth}}}/A$ was 0.27 Ts for the hydrogen case and 0.28 Ts for the deuterium case, i.e. they were the same, within errors, in both plasmas. These identity experiments also confirm that ρ*, β, ν*, q are the only significant parameters governing heat transport in these L-mode plasmas. We note that the equality of
$B{\tau _{\textrm{Eth}}}/A$ was 0.27 Ts for the hydrogen case and 0.28 Ts for the deuterium case, i.e. they were the same, within errors, in both plasmas. These identity experiments also confirm that ρ*, β, ν*, q are the only significant parameters governing heat transport in these L-mode plasmas. We note that the equality of ![]() $B{\tau _{\textrm{Eth}}}/A$ (or locally of A χ/B) at fixed ρ*, β, ν*, q does not, on it's own, qualify the nature of the underlying transport (gyroBohm, Bohm-like or other) as can be achieved with a scan of ρ* (Petty et al. Reference Petty, Luce, Pinsker, Burrell, Chiu, Gohil, James and Wroblewski1995; Cordey et al. Reference Cordey, Balet, Campbell, Challis, Christiansen, Gormezano, Gowers, Muir, Righi, Saibene, Stubberfield and Thomsen1996). Predictive modelling with JETTO-TGLF of the isotope identity pair, with boundary conditions imposed at ρ = 0.8, is in very good agreement with experiment for both isotopes, for both the particle and energy transport. The reader is referred to Maggi et al. (Reference Maggi, Weisen, Casson, Auriemma, Lorenzini, Nordman, Delabie, Eriksson, Flanagan and Keeling2019) for details.
$B{\tau _{\textrm{Eth}}}/A$ (or locally of A χ/B) at fixed ρ*, β, ν*, q does not, on it's own, qualify the nature of the underlying transport (gyroBohm, Bohm-like or other) as can be achieved with a scan of ρ* (Petty et al. Reference Petty, Luce, Pinsker, Burrell, Chiu, Gohil, James and Wroblewski1995; Cordey et al. Reference Cordey, Balet, Campbell, Challis, Christiansen, Gormezano, Gowers, Muir, Righi, Saibene, Stubberfield and Thomsen1996). Predictive modelling with JETTO-TGLF of the isotope identity pair, with boundary conditions imposed at ρ = 0.8, is in very good agreement with experiment for both isotopes, for both the particle and energy transport. The reader is referred to Maggi et al. (Reference Maggi, Weisen, Casson, Auriemma, Lorenzini, Nordman, Delabie, Eriksson, Flanagan and Keeling2019) for details.
5. Isotope dependence in JET-ILW type I ELMy H-modes
Due to the limited NBI power in hydrogen (~10 MW), H-mode operation at an unusually low toroidal field for JET was necessary. A so-called ‘corner–corner’ configuration, with strike points near the divertor pumping ducts was chosen for best density control and confinement for most of the discharges. The dataset size is 171 samples in total with subsets at B T = 1 T, Ip = 1 MA (q 95 ≅ 3) and B T = 1.7 T, Ip = 1.4 MA (q 95 ≅ 3.7), a few samples at 1.7 T, 1.7 MA in D only. Deuterium beams were used to heat the deuterium plasmas and hydrogen beam were used to heat the hydrogen plasmas. The power range in deuterium was 3.5 MW ≤ P NBI ≤ 16.6 MW (only NBI) and in hydrogen 3 MW ≤ P NBI ≤ 10.4 MW, 0 ≤ P ICRH ≤ 6.2 MW. The additional ICRH power, provided by second harmonic hydrogen heating, was necessary in some hydrogen discharges to access type I ELMy H-modes at the higher field on 1.7 T. The experiments consisted mostly in systematic scans of the external gas puff rate and power scans. Many of the lower power hydrogen H-modes were in type III ELMy H-mode and were excluded from the dataset. The experimental conditions of these experiments were presented in greater detail in Maggi et al. (Reference Maggi, Weisen, Hillesheim, Chankin, Delabie, Horvath, Auriemma, Carvalho, Corrigan and Flanagan2018).
It turned out to be impossible to produce pairs in hydrogen and deuterium with matched density, except in a few cases, because of the much lower particle confinement for hydrogen H-modes. Figure 6(a) shows the total particle content ![]() ${N_e} = \int {{n_e}\,\textrm{d}V}$ versus the Balmer alpha emission along a horizontal viewing line. There is little overlap in the density ranges obtained in hydrogen and deuterium. Gas puff rates several times larger in hydrogen were often necessary to obtain similar densities. In deuterium H-modes, the gas puff rate did not allow the density to be controlled, unlike hydrogen plasmas, where increased puff rates (and edge particle sources, as seen in figure 6a) did allow increasing the density. The temperatures obtained were similar in both species. This behaviour is in stark contrast to that observed in JT-60U, where the same densities were easily obtained, but temperatures in hydrogen were lower than in deuterium (Urano et al. Reference Urano, Takizuka, Aiba, Kikuchi, Nakano, Fujita, Oyama, Kamada and Hayashi2013). Figure 6(b) shows that the ratio of the fast ion stored energy from NBH, calculated using the PENCIL code (Challis et al. Reference Challis, Cordey, Hamnen, Stubberfield, Christiansen, Lazzaro, Muir, Stork and Thompson1989), scales fairly linearly with the NBH power divided by the particle content P NB/Ne, however in hydrogen the fast ion contribution is lower, which can be understood from the scaling of the slowing down time
${N_e} = \int {{n_e}\,\textrm{d}V}$ versus the Balmer alpha emission along a horizontal viewing line. There is little overlap in the density ranges obtained in hydrogen and deuterium. Gas puff rates several times larger in hydrogen were often necessary to obtain similar densities. In deuterium H-modes, the gas puff rate did not allow the density to be controlled, unlike hydrogen plasmas, where increased puff rates (and edge particle sources, as seen in figure 6a) did allow increasing the density. The temperatures obtained were similar in both species. This behaviour is in stark contrast to that observed in JT-60U, where the same densities were easily obtained, but temperatures in hydrogen were lower than in deuterium (Urano et al. Reference Urano, Takizuka, Aiba, Kikuchi, Nakano, Fujita, Oyama, Kamada and Hayashi2013). Figure 6(b) shows that the ratio of the fast ion stored energy from NBH, calculated using the PENCIL code (Challis et al. Reference Challis, Cordey, Hamnen, Stubberfield, Christiansen, Lazzaro, Muir, Stork and Thompson1989), scales fairly linearly with the NBH power divided by the particle content P NB/Ne, however in hydrogen the fast ion contribution is lower, which can be understood from the scaling of the slowing down time ![]() ${\tau _{\textrm{slow}}}\propto T_e^{3/2}/( \textrm{A}{\textrm{n}_e}) $. The core ion to electron temperature ratio Ti/Te at ρ = 0.3, estimated as
${\tau _{\textrm{slow}}}\propto T_e^{3/2}/( \textrm{A}{\textrm{n}_e}) $. The core ion to electron temperature ratio Ti/Te at ρ = 0.3, estimated as ![]() ${T_{\textrm{ieq}}}(\,{f_i} = 0.2, \;\rho ) /{T_e}( \rho ) $, increases up to near 1.4 with P NB/Ne, as seen in figure 5(c) and is lower in hydrogen plasmas. The figure also shows available CXS measurements, marked with + signs (red of hydrogen, blue for deuterium). They show a similar increase of Ti/Te with P NB/Ne, although there appears to be no systematic difference between the two species.
${T_{\textrm{ieq}}}(\,{f_i} = 0.2, \;\rho ) /{T_e}( \rho ) $, increases up to near 1.4 with P NB/Ne, as seen in figure 5(c) and is lower in hydrogen plasmas. The figure also shows available CXS measurements, marked with + signs (red of hydrogen, blue for deuterium). They show a similar increase of Ti/Te with P NB/Ne, although there appears to be no systematic difference between the two species.

Figure 6. (a) Plasma electron content vs Balmer-α emission as proxy for edge source, (b) ratio of fast ion stored energy to thermal stored energy vs NBH power per particle, (c) core Ti/Te ratio vs NBH power per particle. Full symbols for Ti = T ieq (fi = 0.2, ρ = 0.3), + signs for Ti from CXS.
As good CXS measurements are only available for less than half of the data, we use ![]() ${T_{\textrm{ieq}}}(\, {f_i} = 0.2, \rho) $ for evaluating the ion contribution to the confinement time. For most of the cases where CXS measurements are available
${T_{\textrm{ieq}}}(\, {f_i} = 0.2, \rho) $ for evaluating the ion contribution to the confinement time. For most of the cases where CXS measurements are available ![]() ${T_{\textrm{ieq}}}(\,{f_i} = 0.2, \;\rho ) $ provides a good fit to the measured ion temperatures in this dataset, for both hydrogen and deuterium, as can be seen in figure 5 of Weisen et al. (Reference Weisen, Maggi, Menmuir, Horvath, Bache, Casson, Oberparleiter, Saarelma, Auriemma and Chankin2018). We keep in mind that the uncertainties in Ti may contribute to several per cent of error in global confinement time.
${T_{\textrm{ieq}}}(\,{f_i} = 0.2, \;\rho ) $ provides a good fit to the measured ion temperatures in this dataset, for both hydrogen and deuterium, as can be seen in figure 5 of Weisen et al. (Reference Weisen, Maggi, Menmuir, Horvath, Bache, Casson, Oberparleiter, Saarelma, Auriemma and Chankin2018). We keep in mind that the uncertainties in Ti may contribute to several per cent of error in global confinement time.
5.1. Global thermal confinement in type I ELMy H-mode
The thermal stored energy is calculated as in (4.1). Unlike the case for L-modes, the electron density in deuterium H-modes is essentially uncontrollable using gas puffing (Maggi et al. Reference Maggi, Saarelma, Casson, Challis, de la Luna, Frassinetti, Giroud, Joffrin, Simpson and Beurskens2015; Urano et al. Reference Urano, Hobirk, Maggi and Joffrin2016; Maslov et al. Reference Maslov, Boboc, Brix, Flanagan, Peluso, Price and Romanelli2020). We therefore here avoid ![]() $\langle {n_e}\rangle $ as a regression parameter. Regressions including the density have been presented in Maggi et al. (Reference Maggi, Weisen, Hillesheim, Chankin, Delabie, Horvath, Auriemma, Carvalho, Corrigan and Flanagan2018), Weisen et al. (Reference Weisen, Maggi, Menmuir, Horvath, Bache, Casson, Oberparleiter, Saarelma, Auriemma and Chankin2018), with similar results for the ion mass scaling. Instead, we use the Balmer-α radiation along a horizontal line as a proxy for edge fuelling. The intensity of Balmer-α emission scales with the gas puff rate roughly within a factor 2, over a factor of 20 variation in the dataset, however, better regressions are obtained with the Balmer-α emission than with the gas puff rate. Satisfactory regressions using the divertor Balmer-α radiation or the gas puff rate are also obtained, however, the Balmer-α radiation along a horizontal line provides the regressions with the lowest standard deviation.
$\langle {n_e}\rangle $ as a regression parameter. Regressions including the density have been presented in Maggi et al. (Reference Maggi, Weisen, Hillesheim, Chankin, Delabie, Horvath, Auriemma, Carvalho, Corrigan and Flanagan2018), Weisen et al. (Reference Weisen, Maggi, Menmuir, Horvath, Bache, Casson, Oberparleiter, Saarelma, Auriemma and Chankin2018), with similar results for the ion mass scaling. Instead, we use the Balmer-α radiation along a horizontal line as a proxy for edge fuelling. The intensity of Balmer-α emission scales with the gas puff rate roughly within a factor 2, over a factor of 20 variation in the dataset, however, better regressions are obtained with the Balmer-α emission than with the gas puff rate. Satisfactory regressions using the divertor Balmer-α radiation or the gas puff rate are also obtained, however, the Balmer-α radiation along a horizontal line provides the regressions with the lowest standard deviation.
The regression for W th is shown in figure 7 and given below:
The standard deviation of this regression is 0.09. A very similar result is obtained if we regress for the thermal energy inferred from W MHD as in (4.1)
with a standard deviation of 0.094. (Regression in (5.2) is too similar to (5.1) to deserve its own figure.)
These scalings have a slightly stronger isotope dependence than reported in Maggi et al. (Reference Maggi, Weisen, Hillesheim, Chankin, Delabie, Horvath, Auriemma, Carvalho, Corrigan and Flanagan2018), which found ![]() ${W_{\textrm{th}}}\propto {A^{0.4}}$ using the plasma density rather than a measure of gas fuelling and assuming Ti = Te. The scaling is significantly stronger scaling than in JET-C (JET Team 1999; Saibene et al. Reference Saibene, Horton, Sartori, Balet, Clement, Conway, Cordey, De Esch, Ingesson and Lingertat1999) and in the IPB(y,2) ELMy H-mode scaling
${W_{\textrm{th}}}\propto {A^{0.4}}$ using the plasma density rather than a measure of gas fuelling and assuming Ti = Te. The scaling is significantly stronger scaling than in JET-C (JET Team 1999; Saibene et al. Reference Saibene, Horton, Sartori, Balet, Clement, Conway, Cordey, De Esch, Ingesson and Lingertat1999) and in the IPB(y,2) ELMy H-mode scaling ![]() $( {W_{\textrm{th}}}\propto {A^{0.19}}) $ (ITER Physics Basis 1999). A recent broad survey of H-mode confinement in JET, with 867 JET-ILW samples, including deuterium (the majority) and hydrogen plasmas also reports a strong isotope scaling in JET-ILW, with mass exponents in the range 0.35 to 0.43, depending on the choice of regression variables and data subsets (Maslov et al. Reference Maslov, Boboc, Brix, Flanagan, Peluso, Price and Romanelli2020). In that study, the thermal stored energy was inferred from the diamagnetic energy which is based on external magnetic measurements, corrected for the perpendicular fast ion energy content. Interestingly, that study also finds that the mass exponents are somewhat higher when a measure of gas fuelling is used instead of the plasma density. Altogether, this paper and Maggi et al. (Reference Maggi, Weisen, Hillesheim, Chankin, Delabie, Horvath, Auriemma, Carvalho, Corrigan and Flanagan2018), Maslov et al. (Reference Maslov, Boboc, Brix, Flanagan, Peluso, Price and Romanelli2020), show that isotope scaling of thermal energy confinement in JET-ILW is robust to the choice of data sets and regression variables.
$( {W_{\textrm{th}}}\propto {A^{0.19}}) $ (ITER Physics Basis 1999). A recent broad survey of H-mode confinement in JET, with 867 JET-ILW samples, including deuterium (the majority) and hydrogen plasmas also reports a strong isotope scaling in JET-ILW, with mass exponents in the range 0.35 to 0.43, depending on the choice of regression variables and data subsets (Maslov et al. Reference Maslov, Boboc, Brix, Flanagan, Peluso, Price and Romanelli2020). In that study, the thermal stored energy was inferred from the diamagnetic energy which is based on external magnetic measurements, corrected for the perpendicular fast ion energy content. Interestingly, that study also finds that the mass exponents are somewhat higher when a measure of gas fuelling is used instead of the plasma density. Altogether, this paper and Maggi et al. (Reference Maggi, Weisen, Hillesheim, Chankin, Delabie, Horvath, Auriemma, Carvalho, Corrigan and Flanagan2018), Maslov et al. (Reference Maslov, Boboc, Brix, Flanagan, Peluso, Price and Romanelli2020), show that isotope scaling of thermal energy confinement in JET-ILW is robust to the choice of data sets and regression variables.
The normalised hydrogen and deuterium temperatures are similar, regardless of conditions. In figure 8 we show ∇Te as function of Te for ρ pol = 0.8 and 0.55. As the HRTS system suffered a miscalibration at 3 channels near the pedestal top for part of the data, we show these using data from the LIDAR Thomson scattering system. There is no discernible systematic difference in ∇Te/Te between the two species, nor for the different heat fluxes, which span a factor 9 at ρ = 0.55 (figure 8a). In the meaning of stiffness as defined in Garbet et al. (Reference Garbet, Mantica, Ryter, Cordey, Imbeaux, Sozzi, Manini, Asp, Parail and Wolf2004), we see no evidence for a difference in stiffness between the two species, as already stated in Maggi et al. (Reference Maggi, Weisen, Hillesheim, Chankin, Delabie, Horvath, Auriemma, Carvalho, Corrigan and Flanagan2018).

Figure 8. ∇Te as function of Te for (a) ρ pol = 0.55 and (b) ρ pol = 0.8. The dashed lines correspond to the averages of R ∇Te/Te.
When normalised to the gyroBohm heat flux defined as ![]() ${Q_{\textrm{gB}}} = {( A{m_p}) ^{0.5}}{n_e}{( e{T_i}) ^{2.5}}R/ {L_{\textrm{Ti}}}/( {e^2}{B^2}R_{\textrm{geo}}^2) {R_{\textrm{geo}}}/{L_{\textrm{ref}\,f}}[ \textrm{W}\,{\textrm{m}^{ - 2}}] $ (Garbet et al. Reference Garbet, Mantica, Ryter, Cordey, Imbeaux, Sozzi, Manini, Asp, Parail and Wolf2004), the range of ion heat fluxes in the dataset is even larger, as seen in figure 9 for ρ = 0.6 as function of R/L Ti. For this calculation we adopted L ref = R geo as the reference scale length, assumed the effective surface for the calculation of the heat flux to be S eff = dV/dr, with V the plasma volume, r = (R max − R min)/2 and R geo = (R max − R min)/2, R max and R min being the maxima and minima of the flux surfaces at the plasma mid-plane. Although errors on the normalised heat flux and on R/L Ti are large, we see that the measured gradients are mostly in the range 5 < R/L Ti < 8 for both isotopes over a range of normalised heat fluxes, Qi/Q gB, of a factor 20. No dependence of Qi/Q gB on R/L Ti, nor on the isotope is discernible. A possible species dependence, as reported in Urano et al. (Reference Urano, Takizuka, Aiba, Kikuchi, Nakano, Fujita, Oyama, Kamada and Hayashi2013), is likely to be obscured by a combination of experimental errors and of unresolved dependences of the critical gradient R/L crit (Garbet et al. Reference Garbet, Mantica, Ryter, Cordey, Imbeaux, Sozzi, Manini, Asp, Parail and Wolf2004) on the wide range of plasma conditions in the dataset.
${Q_{\textrm{gB}}} = {( A{m_p}) ^{0.5}}{n_e}{( e{T_i}) ^{2.5}}R/ {L_{\textrm{Ti}}}/( {e^2}{B^2}R_{\textrm{geo}}^2) {R_{\textrm{geo}}}/{L_{\textrm{ref}\,f}}[ \textrm{W}\,{\textrm{m}^{ - 2}}] $ (Garbet et al. Reference Garbet, Mantica, Ryter, Cordey, Imbeaux, Sozzi, Manini, Asp, Parail and Wolf2004), the range of ion heat fluxes in the dataset is even larger, as seen in figure 9 for ρ = 0.6 as function of R/L Ti. For this calculation we adopted L ref = R geo as the reference scale length, assumed the effective surface for the calculation of the heat flux to be S eff = dV/dr, with V the plasma volume, r = (R max − R min)/2 and R geo = (R max − R min)/2, R max and R min being the maxima and minima of the flux surfaces at the plasma mid-plane. Although errors on the normalised heat flux and on R/L Ti are large, we see that the measured gradients are mostly in the range 5 < R/L Ti < 8 for both isotopes over a range of normalised heat fluxes, Qi/Q gB, of a factor 20. No dependence of Qi/Q gB on R/L Ti, nor on the isotope is discernible. A possible species dependence, as reported in Urano et al. (Reference Urano, Takizuka, Aiba, Kikuchi, Nakano, Fujita, Oyama, Kamada and Hayashi2013), is likely to be obscured by a combination of experimental errors and of unresolved dependences of the critical gradient R/L crit (Garbet et al. Reference Garbet, Mantica, Ryter, Cordey, Imbeaux, Sozzi, Manini, Asp, Parail and Wolf2004) on the wide range of plasma conditions in the dataset.

Figure 9. Ion heat flux in gyroBohm units vs normalised ion temperature gradient at ρ = 0.6.
The density profiles of hydrogen and deuterium plasmas are remarkably similar too. The volume average density can be regressed as ![]() $\langle {n_e}\rangle = 0.92{n_e}( 0.9) + 0.35 \times {10^{19}}\,{\textrm{m}^{ - 3}}$ for both species, as seen in figure 10. (This implies that plasmas with lower density have somewhat more peaked density profiles.) Together with the similarity of temperature profiles, this implies that the global electron energy is proportional to the electron energy at ρ pol = 0.9, which we take as a proxy of the pedestal electron energy (figure 11). The ratios of the pedestal to global stored electron energies for both species are well within error bars,
$\langle {n_e}\rangle = 0.92{n_e}( 0.9) + 0.35 \times {10^{19}}\,{\textrm{m}^{ - 3}}$ for both species, as seen in figure 10. (This implies that plasmas with lower density have somewhat more peaked density profiles.) Together with the similarity of temperature profiles, this implies that the global electron energy is proportional to the electron energy at ρ pol = 0.9, which we take as a proxy of the pedestal electron energy (figure 11). The ratios of the pedestal to global stored electron energies for both species are well within error bars, ![]() ${W_{\textrm{pede}}}/{W_{\textrm{th}}} \approx 0.56$ in deuterium and
${W_{\textrm{pede}}}/{W_{\textrm{th}}} \approx 0.56$ in deuterium and ![]() ${W_{\textrm{pede}}}/{W_{\textrm{th}}} \approx 0.54$ in hydrogen. Hence, to within measurement errors, the species related differences in electron stored energy are attributable to differences in the pedestal. Ion temperatures are less stiff as Ti/Te increases with
${W_{\textrm{pede}}}/{W_{\textrm{th}}} \approx 0.54$ in hydrogen. Hence, to within measurement errors, the species related differences in electron stored energy are attributable to differences in the pedestal. Ion temperatures are less stiff as Ti/Te increases with ![]() $P/\langle {n_e}\rangle $ more strongly in the core than nearer the pedestal top. Assuming T ieq(fi = 0.2, ρ)/Te(ρ), this increase would be stronger for deuterium than for hydrogen as seen in figure 6(c), contributing, albeit very modestly, to better global confinement in deuterium. Unfortunately, accurate core ion temperature measurements, not available at this time, are required for backing up this conjecture.
$P/\langle {n_e}\rangle $ more strongly in the core than nearer the pedestal top. Assuming T ieq(fi = 0.2, ρ)/Te(ρ), this increase would be stronger for deuterium than for hydrogen as seen in figure 6(c), contributing, albeit very modestly, to better global confinement in deuterium. Unfortunately, accurate core ion temperature measurements, not available at this time, are required for backing up this conjecture.

Figure 10. Scaling of average density with pedestal density.

Figure 11. Proportionality of global and pedestal stored energies.
5.2. Momentum confinement in type I ELMy H-mode
Fortunately, the errors on angular velocity determined from CXS are lower than those on Ti and measurements are available for about half of the H-mode dataset. The maximum torque in the dataset was 20 Nm in deuterium and 12 Nm in hydrogen at the maximum NBH powers available. The global momentum ranged up to 4.7 Nms in deuterium and 1.8 Nms in hydrogen. Global angular momentum in hydrogen plasmas is considerably lower than in deuterium plasmas due to the lower NBH torque, the lower density and confinement.
The total momentum L was obtained by volume integration of the local toroidal momentum density ![]() $l = {\omega _\phi }{\rho _m}{R^2}$, where ωϕ is the toroidal angular velocity from CXS, ρm the plasma mass density and R the distance from the torus axis. Figure 12 shows that the global momentum confinement time τϕ = L/T, where T is the NBH torque calculated by PENCIL (Challis et al. Reference Challis, Cordey, Hamnen, Stubberfield, Christiansen, Lazzaro, Muir, Stork and Thompson1989), can range between 0.6 and 1.3 times the thermal energy confinement time, consistently with earlier observations which show χϕ ~ 0.8 χi (Weisen et al. Reference Weisen, Camenen, Salmi, Versloot, Devries, Maslov, Tala, Beurskens and Giroud2012). A close relationship between the isotope scaling of energy and momentum confinement has already been observed in ASDEX (Bessenrodt-Weberpals et al. Reference Bessenrodt-Weberpals and Wagner1993). The highest ratios τϕ/τE are obtained at the lowest ELM frequencies. As ELM frequencies correlate with gas puff rates and densities, the highest ratios τϕ/τE also correspond to the lowest gas puff rates and the highest densities.
$l = {\omega _\phi }{\rho _m}{R^2}$, where ωϕ is the toroidal angular velocity from CXS, ρm the plasma mass density and R the distance from the torus axis. Figure 12 shows that the global momentum confinement time τϕ = L/T, where T is the NBH torque calculated by PENCIL (Challis et al. Reference Challis, Cordey, Hamnen, Stubberfield, Christiansen, Lazzaro, Muir, Stork and Thompson1989), can range between 0.6 and 1.3 times the thermal energy confinement time, consistently with earlier observations which show χϕ ~ 0.8 χi (Weisen et al. Reference Weisen, Camenen, Salmi, Versloot, Devries, Maslov, Tala, Beurskens and Giroud2012). A close relationship between the isotope scaling of energy and momentum confinement has already been observed in ASDEX (Bessenrodt-Weberpals et al. Reference Bessenrodt-Weberpals and Wagner1993). The highest ratios τϕ/τE are obtained at the lowest ELM frequencies. As ELM frequencies correlate with gas puff rates and densities, the highest ratios τϕ/τE also correspond to the lowest gas puff rates and the highest densities.

Figure 12. Angular momentum confinement time vs thermal energy confinement time. The symbols refer to ELM frequencies. Hydrogen plasmas are marked with an additional red circle. The broken lines corespond to τϕ/τE = 0.6 and 1.3, respectively.
Momentum confinement is very similar to the global energy confinement (see (5.1)), as seen in figure 13, where the total momentum was regressed as

Figure 13. Regression for global angular momentum L in Nms in ELMy H-modes correponding to (5.3).
This is significant as momentum is not transported by electrons, showing that the electrons cannot be responsible for the majority of heat transport in these discharges. The dominance of ion transport in JET discharges has also been documented in a comprehensive study of the interspecies power balance in JET (Weisen et al. Reference Weisen, Delabie, Flanagan, Giroud, Maslov, Menmuir, Patel, Scott, Siren and Varje2020) and is consistent with the ITG regime being the dominant transport regime in most JET plasmas with dominant NBH. The negative dependency on Γ of Lϕ in (5.3) is stronger than that of W th in (5.1). It is not clear whether this is a result of ELM losses, which may have an electromagnetic component not shared with the thermal plasma, or a result of charge exchange losses.
5.3. Particle confinement in type I ELMy H-modes
The particle content can be regressed as
where f ELM is the ELM frequency and Γ the Balmer-α emission from the divertor, measured using arrays vertically viewing both the inner and the outer divertor (figure 14).

Figure 14. Regression for the total electron content according to (5.4). Dadiv stands for divertor Balmer-α emission and felm for the ELM frequency.
The isotope mass is the most important contributor to this scaling (STR = 0.66), well ahead of the ELM frequency (STR = 0.28), showing that the differences in ELM frequency are not the only cause (and most likely not the main cause) for the lower density in hydrogen type I ELMy H-modes at low triangularity, as in these experiments. Remarkably, neither the heating power, nor the plasma current appear to have an impact on particle confinement, despite the proximity of a fraction of the cases to the Greenwald density limit (Greenwald et al. Reference Greenwald, Terry, Wolfe, Ejima, Bell, Kaye and Neilson1988). There is also no significant correlation between Ip and Γ.
The isotope dependence of particle confinement is similar to that for energy and momentum and suggest that the poor energy and momentum confinement in hydrogen H-modes may be due to the low particle confinement, in particular in the pedestal. Lower pedestal densities in hydrogen, combined with similar, stiff temperature profiles would lead to lower energy confinement. However, such a narrative would not fit JT-60U results, from which no such difference in particle confinement is reported (Urano et al. Reference Urano, Takizuka, Aiba, Kikuchi, Nakano, Fujita, Oyama, Kamada and Hayashi2013), but instead, a difference in temperatures. At present the difference with JT-60U is not understood, and we limit our comparison to pointing out a few of the differences between the two devices, including the usage of carbon plasma facing components (PFCs) in JT60-U, a substantially larger toroidal field ripple in JT60-U leading to fast ion losses, which induce a torque directed counter to Ip, the usage of near perpendicularly injected low torque NBH for hydrogen, reinforcing fast ion losses. The JT-60U hydrogen plasmas were slowly counter-rotating ![]() $( {\omega _\phi }\sim{-} {10^4}\;\textrm{rad}\,{\textrm{s}^{ - 1}}) $, while the deuterium plasmas were slowly co-rotating
$( {\omega _\phi }\sim{-} {10^4}\;\textrm{rad}\,{\textrm{s}^{ - 1}}) $, while the deuterium plasmas were slowly co-rotating ![]() $( {\omega _\phi }\sim + 10^4\;\textrm{rad}\,{\textrm{s}^{ - 1}}) $ (Urano et al. Reference Urano, Takizuka, Aiba, Kikuchi, Nakano, Fujita, Oyama, Kamada and Hayashi2013). JET ELMy H-modes plasmas with comparable NBH power co-rotated at much higher frequencies, ωϕ ranging from 3 to 7 × 104 rad s−1.
$( {\omega _\phi }\sim + 10^4\;\textrm{rad}\,{\textrm{s}^{ - 1}}) $ (Urano et al. Reference Urano, Takizuka, Aiba, Kikuchi, Nakano, Fujita, Oyama, Kamada and Hayashi2013). JET ELMy H-modes plasmas with comparable NBH power co-rotated at much higher frequencies, ωϕ ranging from 3 to 7 × 104 rad s−1.
Here, our liberal use of the Balmer-α emission as a proxy for the particle source deserves a discussion. This method is based on the approximate proportionality of Balmer-α photon emission rates and hydrogen isotope ionisation rates (Johnson & Hinnov Reference Johnson and Hinnov1973). We find that in the above regressions, this emission leads to narrower fits than the usage of the gas injection rate into the vessel and therefore accept them as better proxies for the particle flux into the plasma. It is however not clear why, for some cases, the main chamber Balmer-α emission provides narrower regressions than the divertor radiation or vice versa. Strictly speaking, the edge source should only be inferred from Balmer-α emission from inside the last closed flux surface (LCFS). In practice this is close to impossible, except if tomographically inverted Balmer-α emission data from a tangentially viewing visible camera equipped with an interference filter are available, which was not the case for this study. Hence the light collected along single vertical or horizontal viewing lines will contain both emission from inside and outside the LCFS. The uncertainties concerning the spatial origin of this light are further acerbated by reflections at the metallic vessel walls. Divertor emission in the dataset is two orders of magnitude larger than main chamber emission, hence most of the light collected by divertor views originates from outside the LCFS. We therefore interpret divertor Balmer-α light as a likely proxy for the neutral density outside the LCFS, which is also proportional to the particle flux into the plasma.
5.4. Transport in mixed isotope ELMy H-modes
Experiments at Ip = 1.4 MA and B T = 1.7 T with 8–10 MW of NBH in mixed hydrogen/deuterium plasmas have allowed to scan the effective mass ![]() ${A_{\textrm{eff}}} = {\sum _i}{A_i}{n_i}/{\sum _i}{n_i}$ (for i = 1, 2) from 1 to 2 (King et al. Reference King, Viezzer, Baruzzo, Belonohy, Buchanan, Carvalho, Cave-Ayland, Coffey, Challis and Delabie2017, Reference King, Viezzer, Balboa, Baruzzo, Belonohy, Buchanan, Carvalho, Cave-Ayland, Coffey and Challis2020). The isotope composition was inferred from the line intensity ratios of the Balmer-α lines of the two species, as measured from high resolution divertor spectroscopy (Neverov et al. Reference Neverov, Kukushkin, Stamp, Alekseev, Brezinsek and von Hellermann2017). Below 10 MW, in pure hydrogen, a type I ELMy regime was not always achieved. Instead, these plasmas had type III ELMs and W th ~ 0.8 MW. The pure hydrogen point, as well as the deuterium one, were taken from equivalent plasmas in the dataset presented in §§ 5.2–5.4. The thermal stored energy in these discharges does not rise linearly with A eff, instead exhibiting a plateau with near constant stored energy for 1.2 ≤ A eff ≤ 1.8, seen in figure 15 for 8 ≤ P NBH ≤ 10 MW (King et al. Reference King, Viezzer, Balboa, Baruzzo, Belonohy, Buchanan, Carvalho, Cave-Ayland, Coffey and Challis2020). While the plateau stored energy is constant, however, the pedestal density rises from near 2.3 × 1019 m−3 for A eff < 1.5 to ~3 × 1019 m−3 for A eff = 1.85, while at the same time the pedestal temperature drops from ~0.6 keV to 0.5 keV (King et al. Reference King, Viezzer, Balboa, Baruzzo, Belonohy, Buchanan, Carvalho, Cave-Ayland, Coffey and Challis2020). The beam species for the mixed plasmas were also mixed, but consisted mostly of hydrogen and where therefore not matched to the bulk plasma composition established by adjusting the gas puff rates for the two species. This mismatch had no incidence of the confinement time, as shown by a comparison of pure hydrogen and pure deuterium injection at the same power into otherwise identical discharges.
${A_{\textrm{eff}}} = {\sum _i}{A_i}{n_i}/{\sum _i}{n_i}$ (for i = 1, 2) from 1 to 2 (King et al. Reference King, Viezzer, Baruzzo, Belonohy, Buchanan, Carvalho, Cave-Ayland, Coffey, Challis and Delabie2017, Reference King, Viezzer, Balboa, Baruzzo, Belonohy, Buchanan, Carvalho, Cave-Ayland, Coffey and Challis2020). The isotope composition was inferred from the line intensity ratios of the Balmer-α lines of the two species, as measured from high resolution divertor spectroscopy (Neverov et al. Reference Neverov, Kukushkin, Stamp, Alekseev, Brezinsek and von Hellermann2017). Below 10 MW, in pure hydrogen, a type I ELMy regime was not always achieved. Instead, these plasmas had type III ELMs and W th ~ 0.8 MW. The pure hydrogen point, as well as the deuterium one, were taken from equivalent plasmas in the dataset presented in §§ 5.2–5.4. The thermal stored energy in these discharges does not rise linearly with A eff, instead exhibiting a plateau with near constant stored energy for 1.2 ≤ A eff ≤ 1.8, seen in figure 15 for 8 ≤ P NBH ≤ 10 MW (King et al. Reference King, Viezzer, Balboa, Baruzzo, Belonohy, Buchanan, Carvalho, Cave-Ayland, Coffey and Challis2020). While the plateau stored energy is constant, however, the pedestal density rises from near 2.3 × 1019 m−3 for A eff < 1.5 to ~3 × 1019 m−3 for A eff = 1.85, while at the same time the pedestal temperature drops from ~0.6 keV to 0.5 keV (King et al. Reference King, Viezzer, Balboa, Baruzzo, Belonohy, Buchanan, Carvalho, Cave-Ayland, Coffey and Challis2020). The beam species for the mixed plasmas were also mixed, but consisted mostly of hydrogen and where therefore not matched to the bulk plasma composition established by adjusting the gas puff rates for the two species. This mismatch had no incidence of the confinement time, as shown by a comparison of pure hydrogen and pure deuterium injection at the same power into otherwise identical discharges.

Figure 15. Thermal stored energy in isotope ratio scan at fixed current and power for H-mode plasmas with type I ELMS. The data points in red are from pure hydrogen and deuterium experiments. From King et al. (Reference King, Viezzer, Balboa, Baruzzo, Belonohy, Buchanan, Carvalho, Cave-Ayland, Coffey and Challis2020).
The plateau is reminiscent of a very similar plateau in L–H threshold power P L-H observed in a different experiment (Hillesheim et al. Reference Hillesheim, Delabie, Solano, Maggi, Meyer, Belonohy, Carvalho, de la Luna, Drenik and Gelfusa2018). This similarity may be linked to general observation that the confinement enhancement factor over IPB98 scaling (ITER Physics Basis 1999) H-modes improves with P/P L-H. These experiments were not repeated to establish the P L-H threshold power, but from similar experiments (Hillesheim et al. Reference Hillesheim, Delabie, Solano, Carvalho, Drenik, Giroud, Huber, Lerche, Lomanowski and Mantsinen2017) we estimate that in pure hydrogen plasmas P L-H was barely exceeded, while for pure D it was higher than 2.
In several of the H-mode experiments deuterium NBH was used with a hydrogen background plasma. The core isotope composition was inferred from the measured neutron rates, showing that it only modestly exceeded the one measured using divertor Balmer-α spectroscopy (Maslov et al. Reference Maslov, King, Viezzer, Keeling, Giroud, Tala, Salmi, Marin, Citrin and Bourdelle2018). As a result the shape of both ion isotope profiles remained close to that of the electrons. Transport simulations and quasilinear gyrokinetic modelling of the isotope profiles in these experiments have shown that the ion particle diffusion coefficient Di can be as high as 2χ eff in the ITG mode, which, combined with strong inward convection leads to fast isotope mixing throughout the plasma cross-section (Bourdelle et al. Reference Bourdelle, Bourdelle, Camenen, Citrin, Marin, Casson, Koechl and Maslov2018; Maslov et al. Reference Maslov, King, Viezzer, Keeling, Giroud, Tala, Salmi, Marin, Citrin and Bourdelle2018; Marin et al. Reference Marin, Citrin, Bourdelle, Camenen, Casson, Ho, Koechl and Maslov2020). This is in stark contrast with the electron particle transport, which governs the electron density profile and is characterised by transport coefficients an order of magnitude smaller than those for the ions. In TEM mode (not the case in these experiments), the ion transport coefficients from gyrokinetic modelling would be much smaller and isotope mixing is expected to be considerably slower (Bourdelle et al. Reference Bourdelle, Bourdelle, Camenen, Citrin, Marin, Casson, Koechl and Maslov2018) as observed in LHD (Ida et al. Reference Ida, Nakata, Tanaka, Yoshinuma, Fujiwara, Sakamoto, Motojima, Masuzaki, Kobayashi and Yamasaki2020). Core isotope ratio control has also been demonstrated by shallow (low penetration) deuterium pellets injected into a plasma simultaneously fuelled by hydrogen gas and hydrogen NBH (Valovic et al. Reference Valovic, Baranov, Boboc, Buchanan, Citrin, Delabie, Frassinetti, Fontdecaba, Garzotti and Giroud2019). A core H/D ratio n H/n D ≈ 1.2, close to the target of n H/n D = 1, was obtained despite the different fuelling methods for the two species, as inferred from core hydrogen isotope CXS and from the neutron rates. Fast mixing greatly eases isotope ratio control, as it matters little (in ITG mode) how and where the main ion species are introduced into the plasma, boding well for isotope ratio control in the upcoming JET D-T experiments and in ITER.
5.5. Particle transport in the H-mode pedestal
Since core temperature profiles are essentially stiff (large variations in the heat flux only lead to small variations of R/LT = R ∇T/T), pedestal conditions are the main contributors to the isotope effect manifested throughout the plasma in these JET-ILW experiments. The pedestal structure, MHD stability and ELM behaviour in hydrogen and deuterium ELMy H-modes have been extensively documented (Horvath Reference Horvath2019; Horvath et al. Reference Horvath, Maggi, Chankin, Saarelma, Field, Aleiferis, Belonohy, Boboc, Corrigan and Delabie2020). We here only summarise finding of direct relevance to the observed reduced particle confinement in hydrogen plasmas. At low ELM frequencies (f ELM < 40 Hz) ELM particle losses increase with ELM frequency, correlating with lower pedestal top densities and showing that the increased ELM frequencies may contribute to lower hydrogen edge densities. Pedestal top densities in both species are similar at similar ELM frequencies. However there is not a unique relationship between the particle loss rate attributable to the ELMs (f ELM ΔN ELM, where ΔN ELM is the number of particles lost per ELM) and the pedestal density, suggesting that other mechanisms, such as particle transport other than by ELMs also play a role (Horvath Reference Horvath2019, PhD thesis; Horvath et al. Reference Horvath, Maggi, Chankin, Saarelma, Field, Aleiferis, Belonohy, Boboc, Corrigan and Delabie2020, sub. NF). This observation is consistent with the regression (5.4), which identifies the ELMs as a significant, but not the main, player in determining the plasma particle content.
The necessity for stronger fuelling in hydrogen is at odds with popular conceptions of fuelling by neutral penetration, as for all other parameters being equal (e.g. Ti), hydrogen neutrals should penetrate deeper into the plasma, thanks to their greater thermal velocity. The observation suggests that transport processes in the pedestal may overcome the effect of thermal velocity. The pedestal width model (Groebner et al. Reference Groebner, Mahdavi, Leonard and Osborne2002) based on neutral penetration is inconsistent with observations of hydrogen and deuterium pedestals. This model predicts a pedestal width scaling as ![]() $\;{\Delta _{\textrm{ne}}}\propto {v_n}r_i^{ - 1}n_{e\,\textrm{ped}}^{ - 1}\propto {A^{ - 1/2}}n_{e\,\textrm{ped}}^{ - 1}$, where
$\;{\Delta _{\textrm{ne}}}\propto {v_n}r_i^{ - 1}n_{e\,\textrm{ped}}^{ - 1}\propto {A^{ - 1/2}}n_{e\,\textrm{ped}}^{ - 1}$, where ![]() $v_n$ is the neutral velocity and ri the ionisation rate, which is temperature dependent. At 1.4 MA/1.7 T there is no clear dependence of Δne on species, nor on
$v_n$ is the neutral velocity and ri the ionisation rate, which is temperature dependent. At 1.4 MA/1.7 T there is no clear dependence of Δne on species, nor on ![]() ${n_{e\,\textrm{ped}}}$. In the 1 MA/1 T subset the measured widths, taken shortly before the ELM crashes, deviate by a factor two from the scaling (see e.g. figure 11 in Weisen et al. Reference Weisen, Maggi, Menmuir, Horvath, Bache, Casson, Oberparleiter, Saarelma, Auriemma and Chankin2018). This remains the case even when the effects of the temperature dependent neutral velocity and ionisation rates are taken into account (Horvath Reference Horvath2019, PhD thesis; Horvath et al. Reference Horvath, Maggi, Chankin, Saarelma, Field, Aleiferis, Belonohy, Boboc, Corrigan and Delabie2020). This shows that the pedestal density width cannot be inferred from neutral penetration alone. We conclude that transport processes, still poorly understood, also contribute to shaping the pedestal.
${n_{e\,\textrm{ped}}}$. In the 1 MA/1 T subset the measured widths, taken shortly before the ELM crashes, deviate by a factor two from the scaling (see e.g. figure 11 in Weisen et al. Reference Weisen, Maggi, Menmuir, Horvath, Bache, Casson, Oberparleiter, Saarelma, Auriemma and Chankin2018). This remains the case even when the effects of the temperature dependent neutral velocity and ionisation rates are taken into account (Horvath Reference Horvath2019, PhD thesis; Horvath et al. Reference Horvath, Maggi, Chankin, Saarelma, Field, Aleiferis, Belonohy, Boboc, Corrigan and Delabie2020). This shows that the pedestal density width cannot be inferred from neutral penetration alone. We conclude that transport processes, still poorly understood, also contribute to shaping the pedestal.
EDGE2D EIRENE (Simonini et al. Reference Simonini, Corrigan, Radford, Spence and Taroni1994; Wiesen Reference Wiesen2006) was used to model the plasma boundary and pedestal region of a pair of H-modes in the two species. Both species required a transport barrier to model the pedestal and near SOL of 3 cm width. In hydrogen the required particle diffusion coefficient was as much as 5 times higher than in deuterium. When only the isotope was changed to hydrogen in a simulation for deuterium, there was only a modest change in Te and ne profiles, which was opposite in sign to the observations. The analysis shows that plasma density profiles in the boundary are governed also by particle transport processes and are more complex than expected from neutral fuelling physics only. We expect better insights into the nature of transport in the H-mode pedestal and its dependence on the isotope species from gyrokinetic modelling (like the one in Bonanomi et al. Reference Bonanomi, Angioni, Crandall, Di Siena, Maggi and Schneider2019b, for the L-mode edge) in conjunction with the application of MHD stability constraints.
5.6. Nonlinear gyrokinetic modelling of core heat transport in hydrogen and deuterium type I ELMy H-modes
A pair of hydrogen and deuterium discharges with same heating power (10 MW) from the type I ELMy H-mode dataset, has been analysed with flux-tube simulations at ρ = 0.5 using the gyrokinetic code GENE (Jenko et al. Reference Jenko, Dorland, Kotschenreuther and Rogers2000; Görler et al. Reference Görler, Lapillonne, Brunner, Dannert, Jenko, Merz and Told2011) and assuming Ti = Te. The hydrogen plasma had a lower volume average density, electron temperature and thermal stored energy (![]() $\langle {n_e}\rangle = 2.1 \times {10^{19}}\;{\textrm{m}^{ - 3}}$,
$\langle {n_e}\rangle = 2.1 \times {10^{19}}\;{\textrm{m}^{ - 3}}$, ![]() ${T_e}( 0) = 2.9\;\textrm{keV}, \;\;{W_{\textrm{th}}} = 1.25\;\textrm{MJ}$) than the deuterium plasma (
${T_e}( 0) = 2.9\;\textrm{keV}, \;\;{W_{\textrm{th}}} = 1.25\;\textrm{MJ}$) than the deuterium plasma (![]() $\langle {n_e}\rangle = 2.8 \times {10^{19}}\;{\textrm{m}^{ - 3}}$,
$\langle {n_e}\rangle = 2.8 \times {10^{19}}\;{\textrm{m}^{ - 3}}$,![]() ${T_e}( 0) = 3.9\;\textrm{keV}, \;\;{W_{\textrm{th}}} = 2.34\;\textrm{MJ}$). Linear simulations including the effect of collisions show no significant deviations from Gyro-Bohm scaling. Nonlinear electromagnetic simulations including the effect of collisions using the standard drift-kinetic Landau–Boltzmann collision operator, E × B shear from the sheared rotation measured by CXS and dilution by Be impurities using the experimental temperature gradients lead to an over-prediction of the measured heat fluxes by a factor 2 for hydrogen and a factor 6 for deuterium, as seen in figure 16.
${T_e}( 0) = 3.9\;\textrm{keV}, \;\;{W_{\textrm{th}}} = 2.34\;\textrm{MJ}$). Linear simulations including the effect of collisions show no significant deviations from Gyro-Bohm scaling. Nonlinear electromagnetic simulations including the effect of collisions using the standard drift-kinetic Landau–Boltzmann collision operator, E × B shear from the sheared rotation measured by CXS and dilution by Be impurities using the experimental temperature gradients lead to an over-prediction of the measured heat fluxes by a factor 2 for hydrogen and a factor 6 for deuterium, as seen in figure 16.

Figure 16. Scan of mid-radius heat flux versus normalised gradient ![]() $a/{L_{\textrm{Te}}} ={-} a{\bf \nabla }{T_e}/{T_e}$ calculated by GENE versus temperature gradient, assuming Ti = Te. Orange: hydrogen, blue: deuterium. The experimental points are shown as a diamond (hydrogen) and a dot (deuterium).
$a/{L_{\textrm{Te}}} ={-} a{\bf \nabla }{T_e}/{T_e}$ calculated by GENE versus temperature gradient, assuming Ti = Te. Orange: hydrogen, blue: deuterium. The experimental points are shown as a diamond (hydrogen) and a dot (deuterium).
Figure 16 shows the result of a scan of normalised temperature gradient ![]() $a/{L_{\textrm{Te}}} = a{\bf \nabla }{T_e}/{T_e}$ at ρt = 0.5, where a is the minor radius, performed in order to find a match for the experimental heat flux. They show that the simulated heat fluxes can be approximately matched by reducing the temperature gradients by 20 % in the hydrogen discharge and by 17 % in deuterium. The simulations also show that deuterium transport is stiffer than the hydrogen one, but has the advantage of a higher instability threshold. At the modest heat flux in the experiment, Q tot ≈ 70 kW m−3, below the crossing point where Q tot is the same for both isotopes, this allows for steeper gradients and hence larger temperatures in the deuterium case.
$a/{L_{\textrm{Te}}} = a{\bf \nabla }{T_e}/{T_e}$ at ρt = 0.5, where a is the minor radius, performed in order to find a match for the experimental heat flux. They show that the simulated heat fluxes can be approximately matched by reducing the temperature gradients by 20 % in the hydrogen discharge and by 17 % in deuterium. The simulations also show that deuterium transport is stiffer than the hydrogen one, but has the advantage of a higher instability threshold. At the modest heat flux in the experiment, Q tot ≈ 70 kW m−3, below the crossing point where Q tot is the same for both isotopes, this allows for steeper gradients and hence larger temperatures in the deuterium case.
Figure 17 shows the results from a range of nonlinear flux-tube GENE calculations at mid-radius undertaken to clarify the importance of collisions, E × B shear and dilution by Be impurities. For these calculations the gradients were adjusted, as indicated above, such as to obtain heat fluxes matching those of the experiment (black bars in figure 17). For each discharge, simulations were performed assuming A = 1 and A = 2. In the absence of collisions, the simulated heat fluxes exceed the experimental ones by factors of 4–15 (green bars in figure 17). Collisions are essential for obtaining realistic heat fluxes, as seen when comparing the simulations without collisions (green bars) with those where E × B from sheared toroidal rotation (red) or impurities (orange) were left out. Collisions are seen to enhance the zonal flow shearing rate ωE × B spectra, reducing ITG amplitudes and suppressing TEM modes. Leaving out E × B from sheared toroidal rotation has little effect, except for the simulation of the D discharge wit A = 2 (figure 17b). However the reduction by E × B stabilisation is always larger when A = 2 is chosen in the simulations, than when A = 1 is chosen, consistently with the qualitative sketch in figure 1. Neglecting Be impurities also leads to ~30 % higher heat fluxes (figure 16a), mainly as a result of dilution of the main species.

Figure 17. Summary of nonlinear GENE simulations in hydrogen and deuterium ELMy H-modes. Both discharges were simulated assuming A = 1 and A = 2. Black bars: experimental heat flux (same in (a) and (b)), blue bars: complete simulation with all effects. Other bars: simulations with one or more effects left out. The bars in violet are for a case when both collisions and E × B shear from bulk toroidal rotation are excluded. The divisions of the bars into parts with different shading indicate, from bottom to top, the ion, electron and Be contributions to the total heat flux.
The effect of collisions is to cause a narrowing of the spectra of heat and particle fluxes by a factor 2 for hydrogen and a factor 3–4 for deuterium, as seen in figure 18. The figure shows the spectral heat and particle fluxes for 4 simulations based on the hydrogen experimental case, with (figure 18a,b) and without (figure 18c,d) collisions assuming A = 1 (figure 18a,c) and A = 2 (figure 18b,d). ![]() ${k_y}{\rho _{\textrm{sH}}}$ is the poloidal wavenumber normalised with the ion Larmor radius calculated for hydrogen. The figure shows both the electrostatic heat and particle fluxes (noted Q es and Γ es) and the magnetic flutter components (Q em and Γ em), which are comparatively small. In the absence of collisions, the peak amplitudes of the fluxes are higher for deuterium, although the spectral widths are somewhat smaller. The flux spectra are strongly affected by the collisions, becoming narrower and shifted to higher poloidal wavenumbers:
${k_y}{\rho _{\textrm{sH}}}$ is the poloidal wavenumber normalised with the ion Larmor radius calculated for hydrogen. The figure shows both the electrostatic heat and particle fluxes (noted Q es and Γ es) and the magnetic flutter components (Q em and Γ em), which are comparatively small. In the absence of collisions, the peak amplitudes of the fluxes are higher for deuterium, although the spectral widths are somewhat smaller. The flux spectra are strongly affected by the collisions, becoming narrower and shifted to higher poloidal wavenumbers: ![]() $\langle {k_y}{\rho _{\textrm{sH}}}\rangle \sim 0.42$ and ~0.36 with collisions for A = 1 and 2 respectively and
$\langle {k_y}{\rho _{\textrm{sH}}}\rangle \sim 0.42$ and ~0.36 with collisions for A = 1 and 2 respectively and ![]() $\langle {k_y}{\rho _{\textrm{sH}}}\rangle \sim 0.3$ and ~0.22 without collisions. Spectral amplitudes are only slightly reduced in the presence of collisions, hence the narrower spectra in deuterium are the main cause for the smaller fluxes. This spectral narrowing is due to electron-ion collisions suppressing TEM modes virtually completely. The stark differences between the cases in figure 18 are well apparent in the cross-phase angle α between potential fluctuations and density fluctuations seen in figure 19. The figure shows the probability distribution functions (PDFs) for the cross-phase angle α as function of α and
$\langle {k_y}{\rho _{\textrm{sH}}}\rangle \sim 0.3$ and ~0.22 without collisions. Spectral amplitudes are only slightly reduced in the presence of collisions, hence the narrower spectra in deuterium are the main cause for the smaller fluxes. This spectral narrowing is due to electron-ion collisions suppressing TEM modes virtually completely. The stark differences between the cases in figure 18 are well apparent in the cross-phase angle α between potential fluctuations and density fluctuations seen in figure 19. The figure shows the probability distribution functions (PDFs) for the cross-phase angle α as function of α and ![]() ${k_y}{\rho _{\textrm{sH}}}$, weighted as described in Dannert & Jenko (Reference Dannert and Jenko2005). Outward particle transport occurs essentially for the positive angles in the region
${k_y}{\rho _{\textrm{sH}}}$, weighted as described in Dannert & Jenko (Reference Dannert and Jenko2005). Outward particle transport occurs essentially for the positive angles in the region ![]() ${k_y}{\rho _{\textrm{sH}}} \lt 0.6$. The region
${k_y}{\rho _{\textrm{sH}}} \lt 0.6$. The region ![]() ${k_y}{\rho _{\textrm{sH}}} \gt 0.6$ in figure 19(c,d) (no collisions, no E × B shear) with finite PDF around
${k_y}{\rho _{\textrm{sH}}} \gt 0.6$ in figure 19(c,d) (no collisions, no E × B shear) with finite PDF around ![]() $\alpha ={\pm} {\rm \pi} $ is due to TEMs and is absent in the collisional cases with E × B shear (subplots a and b).
$\alpha ={\pm} {\rm \pi} $ is due to TEMs and is absent in the collisional cases with E × B shear (subplots a and b).

Figure 18. Spectral heat and particle fluxes with collisions and rotational E × B shear (a and b) and without collisions nor E × B shear (c and d), assuming A = 1 (a,c) and A = 2 (b,d).

Figure 19. Probability distributions for the cross-angle between potential and density fluctuations for simulations with collisions and rotational E × B shear (a,b) and without collisions nor E × B shear (c,d), assuming A = 1 (a,c) and A = 2 (b,d).
The resulting rms average of the zonal flow E × B shear rate is only ~10 % larger in deuterium than in hydrogen in the fully collisional case, but ~1.55 times larger in deuterium when normalised to the respective thermal velocities. This suggests that the main contributor to the larger zonal flow E × B shear stabilisation in deuterium is the isotope effect discussed in the introduction ((2.2) and figure 1). The results are little changed when ion-ion collisions are left out of the calculations. With only electron-ion collisions, fluxes are reduced to a level within 15 % of the full collisional case. This indicates that the reduced fluxes are primarily due to TEM suppression by electron-ion collisions.
These local nonlinear GENE simulations at mid-radius show that a reversal of gyroBohm scaling is consistent with the experimental observations. This is highly encouraging, but we should keep in mind that we cannot extrapolate to global scaling from any local core transport model alone. It is very likely that in global nonlinear simulations with experimentally imposed boundary conditions, e.g. at the top of the pedestal, the global confinement will be strongly dependent on the boundary conditions as a result of profile stiffness, i.e. the root cause for the lower transport in deuterium in these plasmas is still to be sought in the pedestal. A different pedestal boundary condition (higher or lower pedestal temperature for the same heat flux) would lead to different core conditions (higher or lower core temperature for the same heat flux).
6. Discussion
Following the JET results reported in Maggi et al. (Reference Maggi, Weisen, Hillesheim, Chankin, Delabie, Horvath, Auriemma, Carvalho, Corrigan and Flanagan2018), progress in data analysis and modelling has confirmed the scalings of the global energy confinement with isotope mass in L-mode (weak) and H-mode (strong) and extended them to include the momentum and the particle confinement. Remarkably, in H-mode all three transport channels, energy, momentum and particle transport, have similar isotope scalings, with mass exponents around 0.5. As a result of the observed and modelled temperature profile stiffness, the origin of global isotope scaling in the JET discharges investigated is sought for in the physics of the pedestal, which is sensitive to recycling, atomic physics processes and MHD stability. Analysis of density pedestal width shows that neutral fuelling physics alone is insufficient to explain the systematic differences between the species, pointing to the importance of transport processes in the pedestal that are species dependent and still need to be understood. Core confinement scales with pedestal conditions as a result of stiff temperature profiles in ITG dominated turbulence. This causes local gyroBohm scaling to be overridden in JETTO-TGLF simulations in L-mode, resulting in a prediction of independence of confinement on the isotope species. In nonlinear flux-tube GENE simulations of the core of H-modes gyroBohm scaling is even reversed by the effect of collisions on zonal flow damping and to a lesser extent to the ωE ×B shear and the effect of impurities.
The lessons from modelling work so far is that, within the realm of GK drift wave turbulence theory, there are several effects that can lead to a breaking gyroBohm scaling. The turbulence stabilising effects of E × B shear, whether from zonal flows or extrinsic (bulk rotation) are stronger for higher isotopic mass, which can lead to a suppression and even a reversal of gyroBohm scaling, depending on fluxes and boundary conditions. Electromagnetic effects at high beta can lead to a de-stiffening of ITG transport, which is stronger for higher ion mass (Garcia et al. Reference Garcia, Görler, Jenko and Giruzzi2017). Core transport must adopt a transport state that is consistent with the boundary conditions (or the imposed local conditions in flux tube simulations) and the fluxes. If the boundary conditions are non-gyroBohm, then the core plasma establishes a corresponding non-gyroBohm transport state, as expected from the high degree of profile stiffness in ITG turbulence. This underlines the importance of understanding edge and pedestal transport and their isotope dependences. One may speculate that the isotope dependence of GK modelled transport in the edge plasma of L-modes also applies to H-modes (Bonanomi et al. Reference Bonanomi, Angioni, Crandall, Di Siena, Maggi and Schneider2019b), however specific simulations of H-mode pedestals will be required for progress. It would also be incorrect to assume that the core transport would always mirror the edge or pedestal transport. Core transport effects like rotational E×B shearing and fast ion electromagnetic stabilisation effects, which are stronger for plasmas with higher isotope mass, may compound the isotope effects at the edge or pedestal, leading to stronger core and global scaling with isotope mass than expected from boundary effects alone.
Unlike size and current scaling in the international databases (ITER Physics Basis 1999; Doyle Reference Doyle, Houlberg, Kamada, Mukhovatov, Osborne, Polevoi, Bateman, Connor, Cordey and Fujita2007; Verdoolaege et al. Reference Verdoolaege, Kaye, Angioni, Kardaun, Ryter, Thomsen, Maslov and Romanelli2018), which are robust ![]() $( {\tau _E}\sim {I_p}{R^{1.6}}) $, there is no unique isotope scaling. The strength of the isotope dependence depends on operational parameters, on the confinement mode (L-mode, H-mode, TFTR ‘supershot’, …), the heating method, momentum injection and rotation, the wall materials and probably other yet to be identified parameters. In particular, edge and pedestal conditions are sensitive to recycling and atomic physics processes in ways which are still poorly understood, differ between devices and are difficult to diagnose and to control. We speculate that the above listed parameters, which vary widely between experiments, are at the origin of the wide range of isotope dependences reported in the literature. Ultimately, our traditional scaling expressions (we are disinclined to call them ‘laws’), must be recognised as unable to capture multiple dependencies resulting from the wide variety of plasma conditions in fusion research devices and the intricate physics of plasma transport.
$( {\tau _E}\sim {I_p}{R^{1.6}}) $, there is no unique isotope scaling. The strength of the isotope dependence depends on operational parameters, on the confinement mode (L-mode, H-mode, TFTR ‘supershot’, …), the heating method, momentum injection and rotation, the wall materials and probably other yet to be identified parameters. In particular, edge and pedestal conditions are sensitive to recycling and atomic physics processes in ways which are still poorly understood, differ between devices and are difficult to diagnose and to control. We speculate that the above listed parameters, which vary widely between experiments, are at the origin of the wide range of isotope dependences reported in the literature. Ultimately, our traditional scaling expressions (we are disinclined to call them ‘laws’), must be recognised as unable to capture multiple dependencies resulting from the wide variety of plasma conditions in fusion research devices and the intricate physics of plasma transport.
Acknowledgement
The authors wish to thank the referee for his/her meticulous and constructive review. This work has been carried out within the framework of the EUROfusion Consortium and has received funding from the EURATOM research and training programmes 2014–2018 and 2019–2020 under grant agreement No 633053. The views and opinions (if any) expressed herein do not necessarily reflect those of the European Commission.
Editor Tunde Fulop thanks the referees for their advice in evaluating this article.
Declaration of interests
The authors report no conflict of interest.