1. Introduction
Quasilinear (QL) descriptions of lower hybrid current drive (LHCD) have successfully predicted and explained how non-inductive currents can be driven in tokamaks (Fisch Reference Fisch1978; Karney & Fisch Reference Karney and Fisch1979, Reference Karney and Fisch1985; Fisch & Boozer Reference Fisch and Boozer1980; Fisch & Karney Reference Fisch and Karney1981; Cordey et al. Reference Cordey, Edlington and Start1982; Antonsen & Chu Reference Antonsen and Chu1982; Taguchi Reference Taguchi1983), although discrepancies remain (Bonoli Reference Bonoli2014). The intense applied radio frequency (RF) fields used to drive the current result in departures of the electron distribution function from Maxwellian, indicating a failure of QL theory (Catto & Tolman Reference Catto and Tolman2021a ,Reference Catto and Tolman b ). The purpose here is to investigate the failure of QL theory and present an alternative description valid for a very intense applied monochromatic lower hybrid wave. A brief analysis of lower hybrid waves appears in the appendix of Catto & Zhou (Reference Catto and Zhou2023).
Before presenting the detailed calculation, it may be useful to provide a few more background details. The pioneering evaluations of LHCD in the late 1970s and early 1980s were for plane waves in homogeneous magnetised plasmas. The QL descriptions used seldom mentioned the need to retain collisions in the linearised kinetic equation, but when the results were applied to tokamak geometry it was normally assumed that successive passes through resonance were uncorrelated. Catto (Reference Catto2020) first realised that the resonant particles were particularly sensitive to collisions and the narrow collisional boundary layer formed that enhanced the role of collisions for them. Subsequent work by Catto & Tolman (Reference Catto and Tolman2021a ,Reference Catto and Tolman b ) extended the collisional treatment to tokamak geometry, and demonstrated that the resonance condition is not local but rather a transit averaged resonance condition. The charges satisfying or nearly satisfying the transit averaged resonance condition are those that are particularly sensitive to collisions which act to decorrelate successive poloidal transits. To lowest order the collision frequency does not enter in QL treatments, but its absence does not mean collisions are not playing a role. The structure of the Fokker–Planck equation for steady state applied wave fields requires collisions to resolve the singular behaviour in the linearised kinetic equation since initial conditions must be unimportant. To demonstrate the role of tokamak geometry Catto & Zhou (Reference Catto and Zhou2023) considered LHCD and used the adjoint procedure of Antonsen & Chiu (Reference Antonsen and Chu1982) with the Cordey et al. (Reference Cordey, Edlington and Start1982) eigenfunctions to get a rigorous result for the trapped fraction corrections to LHCD and to demonstrate that in their absence the usual result was recovered.
To understand why QL theory fails, only a simple nonlinear electron drift kinetic equation (in
![]() $v, {v}_{||}$
variables) for a monochromatic applied parallel electric field
$v, {v}_{||}$
variables) for a monochromatic applied parallel electric field
![]() ${E}_{||}=\tilde{{E}}_{||}\sin (\omega {t}-{k}_{||}{z})$
of frequency
${E}_{||}=\tilde{{E}}_{||}\sin (\omega {t}-{k}_{||}{z})$
of frequency
![]() $\omega$
and parallel wavenumber
$\omega$
and parallel wavenumber
![]() ${k}_{||}$
needs to be considered, namely
${k}_{||}$
needs to be considered, namely
Here
![]() ${f}={f}_{0}+{f}_{1}$
with
${f}={f}_{0}+{f}_{1}$
with
![]() ${f}_{0}({v})$
a Maxwellian and
${f}_{0}({v})$
a Maxwellian and
![]() ${f}_{1}({z},{v},{v}_{||},{t})$
a small correction,
${f}_{1}({z},{v},{v}_{||},{t})$
a small correction,
![]() $\vec {{B}}={B}\vec {{z}}$
is the
$\vec {{B}}={B}\vec {{z}}$
is the
![]() $\vec {{z}}$
directed constant magnetic field,
$\vec {{z}}$
directed constant magnetic field,
![]() ${C}\{{f}_{1}\}$
is the linearised electron collision operator and e and m are the proton charge and electron mass. Defining a resonance width
${C}\{{f}_{1}\}$
is the linearised electron collision operator and e and m are the proton charge and electron mass. Defining a resonance width
![]() $\Delta {v}_{||}$
via
$\Delta {v}_{||}$
via
gives an estimate of
![]() ${f}_{1}$
by balancing the drive and resonance terms:
${f}_{1}$
by balancing the drive and resonance terms:
Resonant electrons are particularly sensitive to collisions. Estimating
with
![]() $\nu _{{e}}$
and
$\nu _{{e}}$
and
![]() ${v}_{{e}}$
the electron collision frequency and thermal speed, and balancing collisions with the resonant term leads to the normalised collisional boundary layer width
${v}_{{e}}$
the electron collision frequency and thermal speed, and balancing collisions with the resonant term leads to the normalised collisional boundary layer width
and effective resonant electron collision frequency
![]() ${\nu _{{\rm eff}}}=\nu _{{e}}{v}_{{e}}^{2}/(\Delta {v}_{||})_{\nu }^{2}\sim \nu _{{e}}({{k}_{||}}{v}_{{e}}/\nu _{{e}})^{2/3}\gg \nu _{{e}}$
.
${\nu _{{\rm eff}}}=\nu _{{e}}{v}_{{e}}^{2}/(\Delta {v}_{||})_{\nu }^{2}\sim \nu _{{e}}({{k}_{||}}{v}_{{e}}/\nu _{{e}})^{2/3}\gg \nu _{{e}}$
.
The nonlinear term ignored in QL theory cannot be neglected when
Inserting (1.3) into (1.6) gives a normalised island width estimate of
QL theory assumes
![]() $(\Delta {v}_{||})_{\nu }\gg (\Delta {v}_{||})_{\mathrm{is}}$
or
$(\Delta {v}_{||})_{\nu }\gg (\Delta {v}_{||})_{\mathrm{is}}$
or
![]() $|\nu _{{e}}/{{k}_{||}}{v}_{{e}}|^{1/3}\gg |{e}\tilde{{E}}_{||}/{mk}_{||}{v}_{{e}}^{2}|^{1/2}$
. However, for fields intense enough to cause the electron distribution function to develop significant non-Maxwellian features this inequality is violated. To verify this, the usual QL diffusivity can be estimated by using
$|\nu _{{e}}/{{k}_{||}}{v}_{{e}}|^{1/3}\gg |{e}\tilde{{E}}_{||}/{mk}_{||}{v}_{{e}}^{2}|^{1/2}$
. However, for fields intense enough to cause the electron distribution function to develop significant non-Maxwellian features this inequality is violated. To verify this, the usual QL diffusivity can be estimated by using
![]() ${D}_{\mathrm{ql}}\sim ({e}\tilde{{E}}_{||}/{m})^{2}\delta (\omega -{k}_{||}{v}_{||})\sim ({e}\tilde{{E}}_{||}/{m})^{2}/{k}_{||}(\Delta {v}_{||})_{\nu }$
, corresponding to the delta function estimate
${D}_{\mathrm{ql}}\sim ({e}\tilde{{E}}_{||}/{m})^{2}\delta (\omega -{k}_{||}{v}_{||})\sim ({e}\tilde{{E}}_{||}/{m})^{2}/{k}_{||}(\Delta {v}_{||})_{\nu }$
, corresponding to the delta function estimate
![]() $\delta (\omega -{k}_{||}{v}_{||})\sim 1/{k}_{||}(\Delta {v}_{||})_{\nu }$
. QL diffusion modifies the electron Maxwellian once the QL and collision operators become comparable, that is, once
$\delta (\omega -{k}_{||}{v}_{||})\sim 1/{k}_{||}(\Delta {v}_{||})_{\nu }$
. QL diffusion modifies the electron Maxwellian once the QL and collision operators become comparable, that is, once
![]() ${D}_{\mathrm{ql}}{f}_{0}\sim \nu _{{e}}{v}_{{e}}^{2}{f}_{0}$
or when
${D}_{\mathrm{ql}}{f}_{0}\sim \nu _{{e}}{v}_{{e}}^{2}{f}_{0}$
or when
This condition is the same as found by allowing the nonlinear, drive and resonant terms to be of the same order,
![]() ${f}_{1}{k}_{||}(\Delta {v}_{||})\sim ({e}\tilde{{E}}_{||}{v}_{||}/{mv})\partial {f}_{0}/\partial {v}\sim ({e}\tilde{{E}}_{||}/{m}){f}_{1}/\Delta {v}_{||}$
, suggesting QL theory is no longer valid. Moreover, it indicates that finite velocity space island effects should be retained because the RF fields are too intense for a QL treatment.
${f}_{1}{k}_{||}(\Delta {v}_{||})\sim ({e}\tilde{{E}}_{||}{v}_{||}/{mv})\partial {f}_{0}/\partial {v}\sim ({e}\tilde{{E}}_{||}/{m}){f}_{1}/\Delta {v}_{||}$
, suggesting QL theory is no longer valid. Moreover, it indicates that finite velocity space island effects should be retained because the RF fields are too intense for a QL treatment.
The ordering
![]() $(\Delta {v}_{||})_{\nu }\sim (\Delta {v}_{||})_{\mathrm{is}}$
is not analytically tractable (Hamilton et al. Reference Hamilton, Tolman, Arzamasskiy and Duarte2023; Catto Reference Catto2024). Consequently, the focus of the following sections is the
$(\Delta {v}_{||})_{\nu }\sim (\Delta {v}_{||})_{\mathrm{is}}$
is not analytically tractable (Hamilton et al. Reference Hamilton, Tolman, Arzamasskiy and Duarte2023; Catto Reference Catto2024). Consequently, the focus of the following sections is the
![]() $(\Delta {v}_{||})_{\mathrm{is}}^{3}\gg (\Delta {v}_{||})_{\nu }^{3}$
limit. The next section introduces notation and derives the nonlinear equation to be solved for a very intense monochromatic wave. Section 3 solves this nonlinear kinetic equation when
$(\Delta {v}_{||})_{\mathrm{is}}^{3}\gg (\Delta {v}_{||})_{\nu }^{3}$
limit. The next section introduces notation and derives the nonlinear equation to be solved for a very intense monochromatic wave. Section 3 solves this nonlinear kinetic equation when
![]() $(\Delta {v}_{||})_{\mathrm{is}}^{3}\gg (\Delta {v}_{||})_{\nu }^{3}$
. In § 4 the lower hybrid driven parallel current and power absorbed to drive the current are evaluated, and the resulting current drive efficiency found. The result is compared with the standard QL expression. The final section is a brief discussion.
$(\Delta {v}_{||})_{\mathrm{is}}^{3}\gg (\Delta {v}_{||})_{\nu }^{3}$
. In § 4 the lower hybrid driven parallel current and power absorbed to drive the current are evaluated, and the resulting current drive efficiency found. The result is compared with the standard QL expression. The final section is a brief discussion.
2. Nonlinear electron kinetic equation
Consider an applied lower hybrid wave of frequency
![]() $\omega \ll \Omega ={eB}/{mc}$
in a uniform plasma with a constant magnetic field
$\omega \ll \Omega ={eB}/{mc}$
in a uniform plasma with a constant magnetic field
![]() $\vec {{B}}={B}\vec {{z}}$
, where B is the magnitude of the magnetic field and
$\vec {{B}}={B}\vec {{z}}$
, where B is the magnitude of the magnetic field and
![]() $\vec {{z}}$
is the unit vector in the direction of the uniform field. For a lowest order Maxwellian distribution function,
$\vec {{z}}$
is the unit vector in the direction of the uniform field. For a lowest order Maxwellian distribution function,
the perturbed distribution function
![]() ${f}_{1}$
satisfies the nonlinear electron drift kinetic equation
${f}_{1}$
satisfies the nonlinear electron drift kinetic equation
in
![]() ${v}_{||}$
and
${v}_{||}$
and
![]() ${v}_{\bot }$
velocity variables with
${v}_{\bot }$
velocity variables with
![]() ${v}^{2}={v}_{||}^{2}+{v}_{\bot }^{2}$
. Here n and T are the electron density and temperature, and
${v}^{2}={v}_{||}^{2}+{v}_{\bot }^{2}$
. Here n and T are the electron density and temperature, and
![]() ${f}_{0}+{f}_{1}={f}$
with
${f}_{0}+{f}_{1}={f}$
with
![]() ${f}_{0}\gg {f}_{1}$
. The perturbing parallel applied electric field of the lower hybrid wave is taken to be
${f}_{0}\gg {f}_{1}$
. The perturbing parallel applied electric field of the lower hybrid wave is taken to be
![]() $\vec {{E}}={E}_{||}\vec {{z}}$
, with the unimportant unperturbed electric field neglected for simplicity.
$\vec {{E}}={E}_{||}\vec {{z}}$
, with the unimportant unperturbed electric field neglected for simplicity.
The collision operator is needed to resolve singular behaviour at a resonance or in the vicinity of small scale velocity space structure. It is approximated by the usual like and unlike terms, namely the high speed expansion (
![]() ${v}^{2}\gg {v}_{{e}}^{2}=2{T}/{m})$
, self adjoint operator
${v}^{2}\gg {v}_{{e}}^{2}=2{T}/{m})$
, self adjoint operator
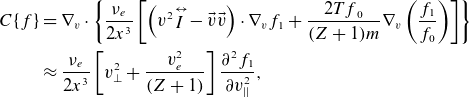 \begin{align}{C}\{{f}\} & =\nabla _{{v}}\cdot \left\{\frac{\nu _{{e}}}{2{x}^{3}}\left[\Big({v}^{2}{\mathop{I}\limits^{\leftrightarrow}}-\vec {{v}}\vec {{v}}\Big)\cdot \nabla _{{v}}{f}_{1}+\frac{2{Tf}_{0}}{({Z}+1){m}}\nabla _{{v}}\left(\frac{{f}_{1}}{{f}_{0}}\right)\right]\right\}\nonumber\\& \approx \frac{\nu _{{e}}}{2{x}^{3}}\left[{v}_{\bot }^{2}+\frac{{v}_{{e}}^{2}}{({Z}+1)}\right]\frac{\partial ^{2}{f}_{1}}{\partial {v}_{||}^{2}},\end{align}
\begin{align}{C}\{{f}\} & =\nabla _{{v}}\cdot \left\{\frac{\nu _{{e}}}{2{x}^{3}}\left[\Big({v}^{2}{\mathop{I}\limits^{\leftrightarrow}}-\vec {{v}}\vec {{v}}\Big)\cdot \nabla _{{v}}{f}_{1}+\frac{2{Tf}_{0}}{({Z}+1){m}}\nabla _{{v}}\left(\frac{{f}_{1}}{{f}_{0}}\right)\right]\right\}\nonumber\\& \approx \frac{\nu _{{e}}}{2{x}^{3}}\left[{v}_{\bot }^{2}+\frac{{v}_{{e}}^{2}}{({Z}+1)}\right]\frac{\partial ^{2}{f}_{1}}{\partial {v}_{||}^{2}},\end{align}
where
![]() ${x}={v}/{v}_{{e}}$
,
${x}={v}/{v}_{{e}}$
,
![]() $\nu _{{e}}=3\sqrt{\pi }({Z}+1)\nu _{{ee}}/4$
and
$\nu _{{e}}=3\sqrt{\pi }({Z}+1)\nu _{{ee}}/4$
and
![]() ${\nu _{{ee}}}=\nu _{{ei}}/{Z}=4\sqrt{2\pi }{e}^{4}{n}\ell \mathrm{n}\,\Lambda _{{c}}/3{m}^{1/2}{T}^{3/2}$
for a quasineutral plasma, with Z the ion charge number and
${\nu _{{ee}}}=\nu _{{ei}}/{Z}=4\sqrt{2\pi }{e}^{4}{n}\ell \mathrm{n}\,\Lambda _{{c}}/3{m}^{1/2}{T}^{3/2}$
for a quasineutral plasma, with Z the ion charge number and
![]() $\ell \mathrm{n}\,\Lambda _{c}$
the Coulomb logarithm. The final form of
$\ell \mathrm{n}\,\Lambda _{c}$
the Coulomb logarithm. The final form of
![]() ${C}\{{f}\}$
is all that is required near the resonance. The high speed expansion of the collision operator was used for the original LHCD calculations (Karney & Fisch Reference Karney and Fisch1979, Reference Karney and Fisch1985) and was also used for a recent linearised treatment of LHCD in a tokamak (Catto & Zhou Reference Catto and Zhou2023) which found that
${C}\{{f}\}$
is all that is required near the resonance. The high speed expansion of the collision operator was used for the original LHCD calculations (Karney & Fisch Reference Karney and Fisch1979, Reference Karney and Fisch1985) and was also used for a recent linearised treatment of LHCD in a tokamak (Catto & Zhou Reference Catto and Zhou2023) which found that
![]() $\omega ^{2}/{k}_{||}^{2}{v}_{{e}}^{2}\approx 5/2$
maximises current drive.
$\omega ^{2}/{k}_{||}^{2}{v}_{{e}}^{2}\approx 5/2$
maximises current drive.
To make analytic progress the applied electric field is assumed to be monochromatic with a wave frequency
![]() $\omega \gt 0$
, and a parallel wave vector
$\omega \gt 0$
, and a parallel wave vector
![]() ${k}_{||}\gt 0$
:
${k}_{||}\gt 0$
:
If only the linearised equation for
![]() ${f}_{1}$
were to be solved as in standard QL theory, it would be adequate to let
${f}_{1}$
were to be solved as in standard QL theory, it would be adequate to let
![]() ${f}_{1}=\mathfrak{I}\mathrm{m}[\tilde{{f}}{\mathrm{e}}^{{i}({{k}_{||}}{z}-\omega {t})}]$
, with
${f}_{1}=\mathfrak{I}\mathrm{m}[\tilde{{f}}{\mathrm{e}}^{{i}({{k}_{||}}{z}-\omega {t})}]$
, with
![]() $\mathfrak{I}\mathrm{m}$
denoting imaginary part, and solve
$\mathfrak{I}\mathrm{m}$
denoting imaginary part, and solve
where only pitch angle scattering need be retained to resolve the singularity at
![]() $\omega ={k}_{||}{v}_{||}$
,
$\omega ={k}_{||}{v}_{||}$
,
![]() ${v}_{\bot {z}}^{2}={v}_{\bot }^{2}+{v}_{{e}}^{2}/({Z}+1)$
and
${v}_{\bot {z}}^{2}={v}_{\bot }^{2}+{v}_{{e}}^{2}/({Z}+1)$
and
![]() $\nu =\nu _{{e}}/2{x}^{3}$
. The solution is (Su & Oberman Reference Su and Oberman1968; Johnston Reference Johnston1971; Auerbach Reference Auerbach1977; Catto Reference Catto2020; Catto & Tolman Reference Catto and Tolman2021b
)
$\nu =\nu _{{e}}/2{x}^{3}$
. The solution is (Su & Oberman Reference Su and Oberman1968; Johnston Reference Johnston1971; Auerbach Reference Auerbach1977; Catto Reference Catto2020; Catto & Tolman Reference Catto and Tolman2021b
)
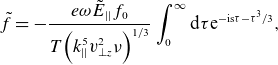 \begin{equation}\tilde{{f}}=-\frac{{e}\omega \tilde{{E}}_{||}{f}_{0}}{{T}\Big({k}_{||}^{5}{v}_{\bot {z}}^{2}\nu \Big)^{1/3}}\int _{0}^{{\infty }}\mathrm{d}\tau \mathrm{e}^{-{\mathrm{is}}\tau -{\tau ^{3}}/3},\end{equation}
\begin{equation}\tilde{{f}}=-\frac{{e}\omega \tilde{{E}}_{||}{f}_{0}}{{T}\Big({k}_{||}^{5}{v}_{\bot {z}}^{2}\nu \Big)^{1/3}}\int _{0}^{{\infty }}\mathrm{d}\tau \mathrm{e}^{-{\mathrm{is}}\tau -{\tau ^{3}}/3},\end{equation}
with
![]() ${s}=({k}_{||}/{v}_{\bot {z}}^{2}\nu )^{1/3}({v}_{||}-\omega /{k}_{||})$
and
${s}=({k}_{||}/{v}_{\bot {z}}^{2}\nu )^{1/3}({v}_{||}-\omega /{k}_{||})$
and
![]() ${s}=1$
giving a velocity space collisional boundary layer width of
${s}=1$
giving a velocity space collisional boundary layer width of
![]() ${v}_{||}-\omega /{k}_{||}=(\Delta {v}_{||})_{\nu }=\big|\nu {v}_{\bot {z}}^{2}/{{k}_{||}}\big|^{1/3}$
.
${v}_{||}-\omega /{k}_{||}=(\Delta {v}_{||})_{\nu }=\big|\nu {v}_{\bot {z}}^{2}/{{k}_{||}}\big|^{1/3}$
.
When the applied lower hybrid wave amplitude becomes large enough, the nonlinear term cannot be neglected and the full nonlinear drift kinetic equation must be considered by letting
![]() ${f}={{f}_{0}}+{f}_{1}$
. Fortunately,
${f}={{f}_{0}}+{f}_{1}$
. Fortunately,
![]() ${f}_{0}$
is slowly varying as is the
${f}_{0}$
is slowly varying as is the
![]() ${v}_{\bot }$
dependence of
${v}_{\bot }$
dependence of
![]() ${f}_{1}$
because the resonance involves only
${f}_{1}$
because the resonance involves only
![]() ${v}_{||}$
. Therefore, the ordering
${v}_{||}$
. Therefore, the ordering
is employed. Assuming a homogeneous plasma such that
with
![]() ${v}_{\bot }$
entering as a parameter, and defining
${v}_{\bot }$
entering as a parameter, and defining
leads to
Now only the last form of (2.3) matters. Letting
![]() ${v}_{||}=\omega /{k}_{||}+{u}$
, with u small, leads to
${v}_{||}=\omega /{k}_{||}+{u}$
, with u small, leads to
To cast this equation into the form considered by Hamilton et al. (Reference Hamilton, Tolman, Arzamasskiy and Duarte2023), let
where
![]() $\sigma ={u}/|{u}|=\pm 1$
or 0, and
$\sigma ={u}/|{u}|=\pm 1$
or 0, and
![]() $\alpha$
is a constant to be determined, to find
$\alpha$
is a constant to be determined, to find
Letting
and
 \begin{equation}\unicode{x1D6E5} =\nu {k}_{||}^{2}{v}_{\bot {z}}^{2}\left|\frac{{m}}{{e}\tilde{{E}}_{||}{k}_{||}}\right|^{3/2}\gt 0\end{equation}
\begin{equation}\unicode{x1D6E5} =\nu {k}_{||}^{2}{v}_{\bot {z}}^{2}\left|\frac{{m}}{{e}\tilde{{E}}_{||}{k}_{||}}\right|^{3/2}\gt 0\end{equation}
gives the equation to be the same as that solved numerically by Hamilton et al. (Reference Hamilton, Tolman, Arzamasskiy and Duarte2023):
For j ∼ 1, (2.14) gives the velocity space island width to be
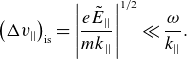 \begin{equation}\big(\Delta {v}_{||}\big)_{\mathrm{is}}=\left|\frac{{e}\tilde{{E}}_{||}}{{mk}_{||}}\right|^{1/2}\ll \frac{\omega }{{k}_{||}}.\end{equation}
\begin{equation}\big(\Delta {v}_{||}\big)_{\mathrm{is}}=\left|\frac{{e}\tilde{{E}}_{||}}{{mk}_{||}}\right|^{1/2}\ll \frac{\omega }{{k}_{||}}.\end{equation}
QL theory assumes that the collisional boundary layer width
is wider than this velocity space island structure, requiring
![]() $\unicode{x1D6E5} =[(\Delta {v}_{||})_{\nu }/$
$\unicode{x1D6E5} =[(\Delta {v}_{||})_{\nu }/$
![]() $(\Delta {v}_{||})_{\mathrm{is}}]^{3}\gg 1$
. However, for a strong applied RF field at low enough density the QL assumption (2.17) fails. In the next section an analytic solution to (2.16) is found in the intense-field limit
$(\Delta {v}_{||})_{\mathrm{is}}]^{3}\gg 1$
. However, for a strong applied RF field at low enough density the QL assumption (2.17) fails. In the next section an analytic solution to (2.16) is found in the intense-field limit
![]() $\unicode{x1D6E5} \ll 1$
.
$\unicode{x1D6E5} \ll 1$
.
3. Solution of the kinetic equation in the intense field limit
The limit where the velocity space island and collisional boundary layer widths are comparable (
![]() $\unicode{x1D6E5} \sim 1$
) is not analytically tractable. However, when the velocity space island width is small, |
$\unicode{x1D6E5} \sim 1$
) is not analytically tractable. However, when the velocity space island width is small, |
![]() $(\Delta {v}_{||})_{\mathrm{is}}/{v}_{{e}}|^{3}\ll 1$
, but larger than the collisional boundary layer width,
$(\Delta {v}_{||})_{\mathrm{is}}/{v}_{{e}}|^{3}\ll 1$
, but larger than the collisional boundary layer width,
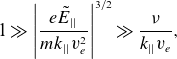 \begin{equation}1\gg \left|\frac{{e}\tilde{{E}}_{||}}{{mk}_{||}{v}_{{e}}^{2}}\right|^{3/2}\gg \frac{\nu }{{{k}_{||}}{v}_{{e}}},\end{equation}
\begin{equation}1\gg \left|\frac{{e}\tilde{{E}}_{||}}{{mk}_{||}{v}_{{e}}^{2}}\right|^{3/2}\gg \frac{\nu }{{{k}_{||}}{v}_{{e}}},\end{equation}
it becomes possible to analytically investigate the failure of QL treatments of LHCD at low density, high temperature and large applied wave amplitudes.
The preceding nonlinear kinetic equation (2.16) with a temporal evolution term has been solved numerically by Hamilton et al. (Reference Hamilton, Tolman, Arzamasskiy and Duarte2023) for an astrophysical application. They also provided a partial analytic steady solution for
![]() $\unicode{x1D6E5} \ll 1$
, which was completed by Catto (Reference Catto2024) for a stellarator transport evaluation. The solution is skew symmetric, satisfying
$\unicode{x1D6E5} \ll 1$
, which was completed by Catto (Reference Catto2024) for a stellarator transport evaluation. The solution is skew symmetric, satisfying
The analytic treatment starts by introducing the reduced constant of the motion or Hamiltonian h defined by
with h = 1 the separatrix between the bound or librating
![]() $({-}1 \lt h \lt 1)$
and the unbound or circulating
$({-}1 \lt h \lt 1)$
and the unbound or circulating
![]() $(h > 1)$
electrons (to avoid confusion, the terminology trapped and passing is avoided and reserved for magnetic wells). The reduced Hamiltonian allows the kinetic equation to be rewritten in terms of
$(h > 1)$
electrons (to avoid confusion, the terminology trapped and passing is avoided and reserved for magnetic wells). The reduced Hamiltonian allows the kinetic equation to be rewritten in terms of
![]() $h,\phi$
variables as
$h,\phi$
variables as
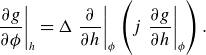 \begin{equation}\left.\frac{\partial {g}}{\partial \phi }\right| _{{h}}=\Delta \left.\frac{\partial }{\partial {h}}\right| _{\phi }\left({j}\left.\frac{\partial {g}}{\partial {h}}\right| _{\phi }\right).\end{equation}
\begin{equation}\left.\frac{\partial {g}}{\partial \phi }\right| _{{h}}=\Delta \left.\frac{\partial }{\partial {h}}\right| _{\phi }\left({j}\left.\frac{\partial {g}}{\partial {h}}\right| _{\phi }\right).\end{equation}
Then
![]() $\unicode{x1D6E5} \ll 1$
suggests a solution of the form
$\unicode{x1D6E5} \ll 1$
suggests a solution of the form
![]() ${g}={g}_{1}({h})+{g}_{2}({h},\phi )+\cdots$
to satisfy
${g}={g}_{1}({h})+{g}_{2}({h},\phi )+\cdots$
to satisfy
![]() $\partial {g}_{1}/\partial \phi |_{{h}}=0$
to lowest order. The next order equation,
$\partial {g}_{1}/\partial \phi |_{{h}}=0$
to lowest order. The next order equation,
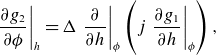 \begin{equation}\left.\frac{\partial {g}_{2}}{\partial \phi }\right| _{{h}}=\Delta \left.\frac{\partial }{\partial {h}}\right| _{\phi }\left({j}\left.\frac{\partial {g}_{1}}{\partial {h}}\right| _{\phi }\right),\end{equation}
\begin{equation}\left.\frac{\partial {g}_{2}}{\partial \phi }\right| _{{h}}=\Delta \left.\frac{\partial }{\partial {h}}\right| _{\phi }\left({j}\left.\frac{\partial {g}_{1}}{\partial {h}}\right| _{\phi }\right),\end{equation}
then leads to the solubility constraint from the collision operator, namely
 \begin{equation}\left.\frac{\partial }{\partial {h}}\right| _{\phi }\left[\left(\oint _{{h}}\mathrm{d}\phi {j}\right)\left.\frac{\partial {g}_{1}}{\partial {h}}\right| _{\phi }\right]=0.\end{equation}
\begin{equation}\left.\frac{\partial }{\partial {h}}\right| _{\phi }\left[\left(\oint _{{h}}\mathrm{d}\phi {j}\right)\left.\frac{\partial {g}_{1}}{\partial {h}}\right| _{\phi }\right]=0.\end{equation}
Therefore,
![]() ${g}_{1}$
is independent of collision frequency, but its form is constrained by collisions.
${g}_{1}$
is independent of collision frequency, but its form is constrained by collisions.
For the bound or librating electrons
![]() ${g}_{1}=0=\alpha =\sigma$
, giving
${g}_{1}=0=\alpha =\sigma$
, giving
![]() ${f}_{1}={u}\partial {f}_{0}/\partial {v}_{||}$
as the only acceptable and well behaved solution. For the freely circulating or unbound electrons, far from the resonance, a solution with
${f}_{1}={u}\partial {f}_{0}/\partial {v}_{||}$
as the only acceptable and well behaved solution. For the freely circulating or unbound electrons, far from the resonance, a solution with
![]() ${g}_{1}\rightarrow ({u}-\sigma \alpha )\partial {f}_{0}/\partial {v}_{||}$
is required, where
${g}_{1}\rightarrow ({u}-\sigma \alpha )\partial {f}_{0}/\partial {v}_{||}$
is required, where
![]() $\sigma =\pm {u}/|{u}|=\pm {j}/|{j}|$
and
$\sigma =\pm {u}/|{u}|=\pm {j}/|{j}|$
and
![]() $\alpha$
is a constant still to be determined. Introducing the complete elliptic function of the second kind, E, leads to (Hamilton et al. Reference Hamilton, Tolman, Arzamasskiy and Duarte2023; Catto Reference Catto2024)
$\alpha$
is a constant still to be determined. Introducing the complete elliptic function of the second kind, E, leads to (Hamilton et al. Reference Hamilton, Tolman, Arzamasskiy and Duarte2023; Catto Reference Catto2024)
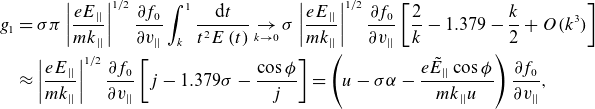 \begin{align}{g}_{1} & =\sigma \pi \left|\frac{{eE}_{||}}{{mk}_{||}}\right|^{1/2}\frac{\partial {f}_{0}}{\partial {v}_{||}}\int _{{k}}^{1}\frac{\mathrm{d}t}{{t}^{2}{E}\left({t}\right)}\underset{{k}\rightarrow 0}{\rightarrow }\sigma \left|\frac{{eE}_{||}}{{mk}_{||}}\right|^{1/2}\frac{\partial {f}_{0}}{\partial {v}_{||}}\left[\frac{2}{{k}}-1.379-\frac{{k}}{2}+{O}({k}^{3})\right]\nonumber\\& \approx \left|\frac{{eE}_{||}}{{mk}_{||}}\right|^{1/2}\frac{\partial {f}_{0}}{\partial {v}_{||}}\left[{j}-1.379\sigma -\frac{\cos \phi }{{j}}\right]=\left({u}-\sigma \alpha -\frac{{e}\tilde{{E}}_{||}\cos \phi }{{mk}_{||}{u}}\right)\frac{\partial {f}_{0}}{\partial {v}_{||}},\end{align}
\begin{align}{g}_{1} & =\sigma \pi \left|\frac{{eE}_{||}}{{mk}_{||}}\right|^{1/2}\frac{\partial {f}_{0}}{\partial {v}_{||}}\int _{{k}}^{1}\frac{\mathrm{d}t}{{t}^{2}{E}\left({t}\right)}\underset{{k}\rightarrow 0}{\rightarrow }\sigma \left|\frac{{eE}_{||}}{{mk}_{||}}\right|^{1/2}\frac{\partial {f}_{0}}{\partial {v}_{||}}\left[\frac{2}{{k}}-1.379-\frac{{k}}{2}+{O}({k}^{3})\right]\nonumber\\& \approx \left|\frac{{eE}_{||}}{{mk}_{||}}\right|^{1/2}\frac{\partial {f}_{0}}{\partial {v}_{||}}\left[{j}-1.379\sigma -\frac{\cos \phi }{{j}}\right]=\left({u}-\sigma \alpha -\frac{{e}\tilde{{E}}_{||}\cos \phi }{{mk}_{||}{u}}\right)\frac{\partial {f}_{0}}{\partial {v}_{||}},\end{align}
with
![]() ${j}=\sqrt{2({h}+\cos \phi )}=(2/{k})\sqrt{1-{k}^{2}\mathrm{sin}^{2}(\phi /2)}$
,
${j}=\sqrt{2({h}+\cos \phi )}=(2/{k})\sqrt{1-{k}^{2}\mathrm{sin}^{2}(\phi /2)}$
,
![]() ${k}=\sqrt{2/({h}+1)}$
,
${k}=\sqrt{2/({h}+1)}$
,
![]() $\int _{-\pi }^{\pi }\mathrm{d}\varphi {j}=\sigma 8{k}^{-1}{E}({k})$
and
$\int _{-\pi }^{\pi }\mathrm{d}\varphi {j}=\sigma 8{k}^{-1}{E}({k})$
and
![]() $\alpha =1.379$
now determined. The unbound solution satisfies
$\alpha =1.379$
now determined. The unbound solution satisfies
![]() ${g}_{1}\rightarrow 0$
at the separatrix (h = 1), but
${g}_{1}\rightarrow 0$
at the separatrix (h = 1), but
![]() $\partial {g}_{1}/\partial {h}|_{\phi }$
and
$\partial {g}_{1}/\partial {h}|_{\phi }$
and
![]() $f_1$
step across it. The narrow collisional boundary layer about the separatrix provides the smooth matching as in the banana regime of neoclassical theory. Moreover, far from the resonance layer
$f_1$
step across it. The narrow collisional boundary layer about the separatrix provides the smooth matching as in the banana regime of neoclassical theory. Moreover, far from the resonance layer
![]() ${f}_{1}({k}\rightarrow 0)\rightarrow 0$
.
${f}_{1}({k}\rightarrow 0)\rightarrow 0$
.
Summarising, the full solution to lowest order (Hamilton et al. Reference Hamilton, Tolman, Arzamasskiy and Duarte2023; Catto Reference Catto2024) is
but now with
![]() $\sigma =\pm {u}/|{u}|=\pm 1$
for the unbound or circulating electrons and
$\sigma =\pm {u}/|{u}|=\pm 1$
for the unbound or circulating electrons and
![]() $\sigma =0$
for the bound or librating electrons. Even though the solution is independent of the collision frequency, its form is determined by the solubility constraint from the collision operator. The
$\sigma =0$
for the bound or librating electrons. Even though the solution is independent of the collision frequency, its form is determined by the solubility constraint from the collision operator. The
![]() $1.379\sigma$
step in the solution
$1.379\sigma$
step in the solution
![]() ${f}_{1}$
at the separatrix is not cancelled by the piecewise continuous behaviour of the derivative
${f}_{1}$
at the separatrix is not cancelled by the piecewise continuous behaviour of the derivative
![]() $\partial {g}_{1}/\partial {h}|_{\phi }$
there. Instead, the step is smoothed by a narrow collisional boundary layer at the separatrix that need not be resolved by the procedure here. The behaviour in the boundary layer does not play a role in the results that follow next.
$\partial {g}_{1}/\partial {h}|_{\phi }$
there. Instead, the step is smoothed by a narrow collisional boundary layer at the separatrix that need not be resolved by the procedure here. The behaviour in the boundary layer does not play a role in the results that follow next.
4. Driven current and power absorbed in the intense field limit
The skew symmetric perturbed solution
![]() ${f}_{1}({u},\phi )=-{f}_{1}({-}{u},-\phi )$
cannot lead to a spatiotemporal averaged density as seen by letting
${f}_{1}({u},\phi )=-{f}_{1}({-}{u},-\phi )$
cannot lead to a spatiotemporal averaged density as seen by letting
![]() ${u}\rightarrow -{u}$
and
${u}\rightarrow -{u}$
and
![]() $\phi \rightarrow -\phi$
, then applying
$\phi \rightarrow -\phi$
, then applying
![]() $\langle \cdots \rangle _{\phi }=\oint \mathrm{d}\phi (\cdots )/2\pi$
at fixed
$\langle \cdots \rangle _{\phi }=\oint \mathrm{d}\phi (\cdots )/2\pi$
at fixed
![]() ${v}_{||}$
and employing
${v}_{||}$
and employing
![]() ${d}^{3}{v}=2\pi {v}_{\bot }{\mathrm{d}v}_{\bot }{\mathrm{d}v}_{||}\propto \mathrm{d}u\propto \mathrm{d}j$
, to form
${d}^{3}{v}=2\pi {v}_{\bot }{\mathrm{d}v}_{\bot }{\mathrm{d}v}_{||}\propto \mathrm{d}u\propto \mathrm{d}j$
, to form
where the limits of the u integration are for the outer limit of the inner-boundary-layer region and, of course, not actually infinite. However, the parallel current requires the u moment
and the extra u means that skew symmetry allows a parallel current! As a result, the driven parallel current is evaluated using
Only the circulating electrons carry current. Moreover, integrating by parts (recalling
![]() ${{j}^{2}}{f}_{1}\propto 1/{j}\rightarrow 0$
far from the separatrix as shown in (3.7)) results in
${{j}^{2}}{f}_{1}\propto 1/{j}\rightarrow 0$
far from the separatrix as shown in (3.7)) results in
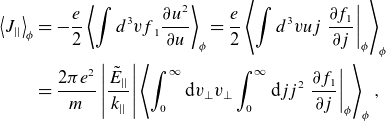 \begin{align}\left\langle {J}_{||}\right\rangle _{\phi } & =-\frac{{e}}{2}\left\langle \int {d}^{3}{vf}_{1}\frac{\partial {u}^{2}}{\partial {u}}\right\rangle _{\phi }=\frac{{e}}{2}\left\langle \int {d}^{3}{vuj}\left.\frac{\partial {f}_{1}}{\partial {j}}\right| _{\phi }\right\rangle _{\phi }\nonumber\\& =\frac{2\pi {e}^{2}}{{m}}\left|\frac{\tilde{{E}}_{||}}{{k}_{||}}\right|\left\langle \int _{0}^{{\infty }}{\mathrm{d}v}_{\bot }{v}_{\bot }\int _{0}^{{\infty }}{\mathrm{d}jj}^{2}\left.\frac{\partial {f}_{1}}{\partial {j}}\right| _{\phi }\right\rangle _{\phi },\end{align}
\begin{align}\left\langle {J}_{||}\right\rangle _{\phi } & =-\frac{{e}}{2}\left\langle \int {d}^{3}{vf}_{1}\frac{\partial {u}^{2}}{\partial {u}}\right\rangle _{\phi }=\frac{{e}}{2}\left\langle \int {d}^{3}{vuj}\left.\frac{\partial {f}_{1}}{\partial {j}}\right| _{\phi }\right\rangle _{\phi }\nonumber\\& =\frac{2\pi {e}^{2}}{{m}}\left|\frac{\tilde{{E}}_{||}}{{k}_{||}}\right|\left\langle \int _{0}^{{\infty }}{\mathrm{d}v}_{\bot }{v}_{\bot }\int _{0}^{{\infty }}{\mathrm{d}jj}^{2}\left.\frac{\partial {f}_{1}}{\partial {j}}\right| _{\phi }\right\rangle _{\phi },\end{align}
where both signs of sigma from j are summed over. Inserting
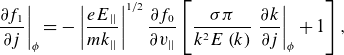 \begin{equation}\left.\frac{\partial {f}_{1}}{\partial {j}}\right| _{\phi }=-\left|\frac{{eE}_{||}}{{mk}_{||}}\right|^{1/2}\frac{\partial {f}_{0}}{\partial {v}_{||}}\left[\frac{\sigma \pi }{{k}^{2}{E}\left({k}\right)}\left.\frac{\partial {k}}{\partial {j}}\right| _{\phi }+1\right],\end{equation}
\begin{equation}\left.\frac{\partial {f}_{1}}{\partial {j}}\right| _{\phi }=-\left|\frac{{eE}_{||}}{{mk}_{||}}\right|^{1/2}\frac{\partial {f}_{0}}{\partial {v}_{||}}\left[\frac{\sigma \pi }{{k}^{2}{E}\left({k}\right)}\left.\frac{\partial {k}}{\partial {j}}\right| _{\phi }+1\right],\end{equation}
leads to
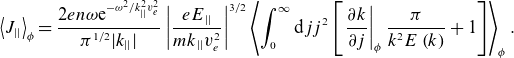 \begin{equation}\left\langle {J}_{||}\right\rangle _{\phi }=\frac{2{en}\omega \mathrm{e}^{-{\omega ^{2}}/{k}_{||}^{2}{v}_{{e}}^{2}}}{\pi ^{1/2}|{k}_{||}|}\left|\frac{{eE}_{||}}{{mk}_{||}{v}_{{e}}^{2}}\right|^{3/2}\left\langle \int _{0}^{{\infty }}{\mathrm{d}jj}^{2}\left[\left.\frac{\partial {k}}{\partial {j}}\right| _{\phi }\frac{\pi }{{k}^{2}{E}\left({k}\right)}+1\right]\right\rangle _{\phi }.\end{equation}
\begin{equation}\left\langle {J}_{||}\right\rangle _{\phi }=\frac{2{en}\omega \mathrm{e}^{-{\omega ^{2}}/{k}_{||}^{2}{v}_{{e}}^{2}}}{\pi ^{1/2}|{k}_{||}|}\left|\frac{{eE}_{||}}{{mk}_{||}{v}_{{e}}^{2}}\right|^{3/2}\left\langle \int _{0}^{{\infty }}{\mathrm{d}jj}^{2}\left[\left.\frac{\partial {k}}{\partial {j}}\right| _{\phi }\frac{\pi }{{k}^{2}{E}\left({k}\right)}+1\right]\right\rangle _{\phi }.\end{equation}
Because the j derivative of k is at fixed
![]() $\phi$
, the
$\phi$
, the
![]() $\phi$
integral can be performed at fixed k or h by using
$\phi$
integral can be performed at fixed k or h by using
![]() $\langle {j}^{2}\rangle _{\phi }=2{h}$
and noting
$\langle {j}^{2}\rangle _{\phi }=2{h}$
and noting
![]() $\partial {k}/\partial {j}|_{\phi }\lt 0$
to find
$\partial {k}/\partial {j}|_{\phi }\lt 0$
to find
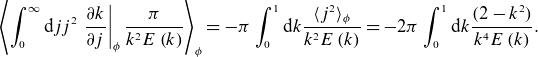 \begin{equation}\left\langle \int _{0}^{{\infty }}{\mathrm{d}jj}^{2}\left.\frac{\partial {k}}{\partial {j}}\right| _{\phi }\frac{\pi }{{k}^{2}{E}\left({k}\right)}\right\rangle _{\phi }=-\pi \int _{0}^{1}{\mathrm{d}k}\frac{\langle {j}^{2}\rangle _{\phi }}{{k}^{2}{E}\left({k}\right)}=-2\pi \int _{0}^{1}{\mathrm{d}k}\frac{(2-{k}^{2})}{{k}^{4}{E}\left({k}\right)}.\end{equation}
\begin{equation}\left\langle \int _{0}^{{\infty }}{\mathrm{d}jj}^{2}\left.\frac{\partial {k}}{\partial {j}}\right| _{\phi }\frac{\pi }{{k}^{2}{E}\left({k}\right)}\right\rangle _{\phi }=-\pi \int _{0}^{1}{\mathrm{d}k}\frac{\langle {j}^{2}\rangle _{\phi }}{{k}^{2}{E}\left({k}\right)}=-2\pi \int _{0}^{1}{\mathrm{d}k}\frac{(2-{k}^{2})}{{k}^{4}{E}\left({k}\right)}.\end{equation}
This procedure removes the awkwardness of the upper limit of the j integral in the outer limit of the inner region. A similar procedure and use of
![]() $\langle {j}\rangle _{\phi }=4\pi ^{-1}{k}^{-1}{E}({k})$
gives
$\langle {j}\rangle _{\phi }=4\pi ^{-1}{k}^{-1}{E}({k})$
gives
As a result, the parallel current is negative (since
![]() $\omega /{k}_{||}\gt 0$
) and given by
$\omega /{k}_{||}\gt 0$
) and given by
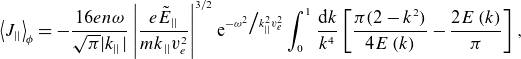 \begin{equation}\left\langle {J}_{||}\right\rangle _{\phi }=-\frac{16{en}\omega }{\sqrt{\pi }|{k}_{||}|}\left|\frac{{e}\tilde{{E}}_{||}}{{mk}_{||}{v}_{{e}}^{2}}\right|^{3/2}{\mathrm{e}}^{-{\omega ^{2}}\big/{k}_{||}^{2}{v}_{{e}}^{2}}\int _{0}^{1}\frac{{\mathrm{d}k}}{{k}^{4}}\left[\frac{\pi (2-{k}^{2})}{4{E}\left({k}\right)}-\frac{2{E}\left({k}\right)}{\pi }\right],\end{equation}
\begin{equation}\left\langle {J}_{||}\right\rangle _{\phi }=-\frac{16{en}\omega }{\sqrt{\pi }|{k}_{||}|}\left|\frac{{e}\tilde{{E}}_{||}}{{mk}_{||}{v}_{{e}}^{2}}\right|^{3/2}{\mathrm{e}}^{-{\omega ^{2}}\big/{k}_{||}^{2}{v}_{{e}}^{2}}\int _{0}^{1}\frac{{\mathrm{d}k}}{{k}^{4}}\left[\frac{\pi (2-{k}^{2})}{4{E}\left({k}\right)}-\frac{2{E}\left({k}\right)}{\pi }\right],\end{equation}
where
Therefore, the lower hybrid driven current for an intense applied field is
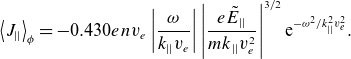 \begin{equation}\left\langle {J}_{||}\right\rangle _{\phi }=-0.430{env}_{{e}}\left|\frac{\omega }{{k}_{||}{v}_{{e}}}\right|\left|\frac{{e}\tilde{{E}}_{||}}{{mk}_{||}{v}_{{e}}^{2}}\right|^{3/2}{\mathrm{e}}^{-{\omega ^{2}}/{k}_{||}^{2}{v}_{{e}}^{2}}.\end{equation}
\begin{equation}\left\langle {J}_{||}\right\rangle _{\phi }=-0.430{env}_{{e}}\left|\frac{\omega }{{k}_{||}{v}_{{e}}}\right|\left|\frac{{e}\tilde{{E}}_{||}}{{mk}_{||}{v}_{{e}}^{2}}\right|^{3/2}{\mathrm{e}}^{-{\omega ^{2}}/{k}_{||}^{2}{v}_{{e}}^{2}}.\end{equation}
Unlike the QL limit for which
![]() $\langle {J}_{||}\rangle _{\phi }\propto 1/\nu _{{e}}$
, the expression for
$\langle {J}_{||}\rangle _{\phi }\propto 1/\nu _{{e}}$
, the expression for
![]() $\langle {J}_{||}\rangle _{\phi }$
is independent of the collision frequency and scales as
$\langle {J}_{||}\rangle _{\phi }$
is independent of the collision frequency and scales as
![]() $\tilde{{E}}_{||}^{3/2}$
.
$\tilde{{E}}_{||}^{3/2}$
.
The RF power absorbed by the electrons is proportional to
![]() $\nu _{{e}}$
, as can be seen by first using
$\nu _{{e}}$
, as can be seen by first using
![]() $2\sin \phi =-{\mathrm{d}j}^{2}/{d}\phi |_{{h}}$
at fixed h to write
$2\sin \phi =-{\mathrm{d}j}^{2}/{d}\phi |_{{h}}$
at fixed h to write
 \begin{align}{P} & =\left\langle {E}_{||}{J}_{||}\right\rangle _{\phi }=-{e}\tilde{{E}}_{||}\left\langle \sin \phi \int {d}^{3}{vv}_{||}{f}\right\rangle _{\phi }\approx \frac{\omega {e}\tilde{{E}}_{||}}{2{k}_{||}}\left\langle \int {d}^{3}{vf}\left.\frac{{\mathrm{d}j}^{2}}{\mathrm{d}\phi }\right| _{{h}}\right\rangle _{\phi }\nonumber\\& =-\frac{\omega {e}\tilde{{E}}_{||}}{2{k}_{||}}\left\langle \int {d}^{3}{vj}^{2}\left.\frac{\partial {g}_{2}}{\partial \phi }\right| _{{h}}\right\rangle _{\phi }=-\frac{\omega {e}\tilde{{E}}_{||}}{2{k}_{||}}\left\langle \int {d}^{3}{v}\Delta {j}^{2}\left.\frac{\partial }{\partial {h}}\right| _{\phi }\left({j}\left.\frac{\partial {g}_{1}}{\partial {h}}\right| _{\phi }\right)\right\rangle _{\phi }.\end{align}
\begin{align}{P} & =\left\langle {E}_{||}{J}_{||}\right\rangle _{\phi }=-{e}\tilde{{E}}_{||}\left\langle \sin \phi \int {d}^{3}{vv}_{||}{f}\right\rangle _{\phi }\approx \frac{\omega {e}\tilde{{E}}_{||}}{2{k}_{||}}\left\langle \int {d}^{3}{vf}\left.\frac{{\mathrm{d}j}^{2}}{\mathrm{d}\phi }\right| _{{h}}\right\rangle _{\phi }\nonumber\\& =-\frac{\omega {e}\tilde{{E}}_{||}}{2{k}_{||}}\left\langle \int {d}^{3}{vj}^{2}\left.\frac{\partial {g}_{2}}{\partial \phi }\right| _{{h}}\right\rangle _{\phi }=-\frac{\omega {e}\tilde{{E}}_{||}}{2{k}_{||}}\left\langle \int {d}^{3}{v}\Delta {j}^{2}\left.\frac{\partial }{\partial {h}}\right| _{\phi }\left({j}\left.\frac{\partial {g}_{1}}{\partial {h}}\right| _{\phi }\right)\right\rangle _{\phi }.\end{align}
In the preceding,
![]() ${v}_{||}=\omega /{k}_{||}+{u}$
and skew symmetry give
${v}_{||}=\omega /{k}_{||}+{u}$
and skew symmetry give
![]() $\langle \int _{-{\infty }}^{{\infty }}\text{d}\textit{uu}\sin\phi {f}_{1}({u},\phi )\rangle _{\phi }=0$
and
$\langle \int _{-{\infty }}^{{\infty }}\text{d}\textit{uu}\sin\phi {f}_{1}({u},\phi )\rangle _{\phi }=0$
and
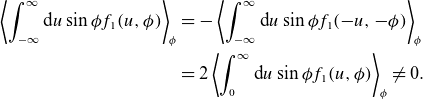 \begin{align}\left\langle \int _{-{\infty }}^{{\infty }}\text{d}u\sin\phi {f}_{1}({u},\phi )\right\rangle _{\phi } & =-\left\langle \int _{-{\infty }}^{{\infty }}\text{d}u\sin\phi {f}_{1}({-}{u},-\phi )\right\rangle _{\phi }\nonumber\\& =2\left\langle \int _{0}^{{\infty }}\text{d}u\sin\phi {f}_{1}({u},\phi )\right\rangle _{\phi }\neq 0.\end{align}
\begin{align}\left\langle \int _{-{\infty }}^{{\infty }}\text{d}u\sin\phi {f}_{1}({u},\phi )\right\rangle _{\phi } & =-\left\langle \int _{-{\infty }}^{{\infty }}\text{d}u\sin\phi {f}_{1}({-}{u},-\phi )\right\rangle _{\phi }\nonumber\\& =2\left\langle \int _{0}^{{\infty }}\text{d}u\sin\phi {f}_{1}({u},\phi )\right\rangle _{\phi }\neq 0.\end{align}
Then
![]() ${u}\propto {j}$
,
${u}\propto {j}$
,
![]() ${j\mathrm{d}j}=\mathrm{d}h$
at fixed
${j\mathrm{d}j}=\mathrm{d}h$
at fixed
![]() $\phi$
and
$\phi$
and
![]() ${h}\underset{{h}\rightarrow {\infty }}{\longrightarrow}2/{k}^{2}$
yield
${h}\underset{{h}\rightarrow {\infty }}{\longrightarrow}2/{k}^{2}$
yield
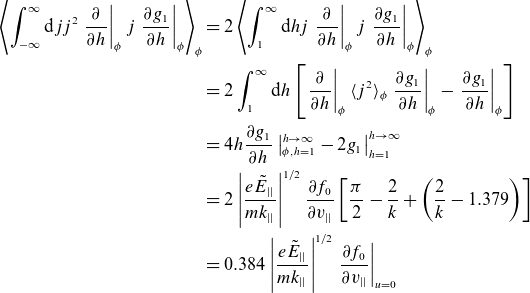 \begin{align}\left\langle \int _{-{\infty }}^{{\infty }}\mathrm{d}jj^{2}\left.\frac{\partial }{\partial {h}}\right| _{\phi }{j}\left.\frac{\partial {g}_{1}}{\partial {h}}\right| _{\phi }\right\rangle _{\phi } & =2\left\langle \int _{1}^{{\infty }}\mathrm{d}hj\left.\frac{\partial }{\partial {h}}\right| _{\phi }{j}\left.\frac{\partial {g}_{1}}{\partial {h}}\right| _{\phi }\right\rangle _{\phi }\nonumber\\& =2\int _{1}^{{\infty }}\mathrm{d}h\left[\left.\frac{\partial }{\partial {h}}\right| _{\phi }\langle {j}^{2}\rangle _{\phi }\left.\frac{\partial {g}_{1}}{\partial {h}}\right| _{\phi }-\left.\frac{\partial {g}_{1}}{\partial {h}}\right| _{\phi }\right]\nonumber\\& =4{h}\frac{\partial {g}_{1}}{\partial {h}}\left| _{\phi ,{h}=1}^{{h}\rightarrow {\infty }}-2{g}_{1}\right| _{{h}=1}^{{h}\rightarrow {\infty }}\nonumber\\& =2\left|\frac{{e}\tilde{{E}}_{||}}{m{k}_{||}}\right|^{1/2}\frac{\partial {f}_{0}}{\partial {v}_{||}}\left[\frac{\pi }{2}-\frac{2}{{k}} +\left(\frac{2}{{k}}-1.379\right)\right]\nonumber\\& =0.384\left|\frac{{e}\tilde{{E}}_{||}}{m{k}_{||}}\right|^{1/2}\left.\frac{\partial {f}_{0}}{\partial {v}_{||}}\right| _{{u}=0}\end{align}
\begin{align}\left\langle \int _{-{\infty }}^{{\infty }}\mathrm{d}jj^{2}\left.\frac{\partial }{\partial {h}}\right| _{\phi }{j}\left.\frac{\partial {g}_{1}}{\partial {h}}\right| _{\phi }\right\rangle _{\phi } & =2\left\langle \int _{1}^{{\infty }}\mathrm{d}hj\left.\frac{\partial }{\partial {h}}\right| _{\phi }{j}\left.\frac{\partial {g}_{1}}{\partial {h}}\right| _{\phi }\right\rangle _{\phi }\nonumber\\& =2\int _{1}^{{\infty }}\mathrm{d}h\left[\left.\frac{\partial }{\partial {h}}\right| _{\phi }\langle {j}^{2}\rangle _{\phi }\left.\frac{\partial {g}_{1}}{\partial {h}}\right| _{\phi }-\left.\frac{\partial {g}_{1}}{\partial {h}}\right| _{\phi }\right]\nonumber\\& =4{h}\frac{\partial {g}_{1}}{\partial {h}}\left| _{\phi ,{h}=1}^{{h}\rightarrow {\infty }}-2{g}_{1}\right| _{{h}=1}^{{h}\rightarrow {\infty }}\nonumber\\& =2\left|\frac{{e}\tilde{{E}}_{||}}{m{k}_{||}}\right|^{1/2}\frac{\partial {f}_{0}}{\partial {v}_{||}}\left[\frac{\pi }{2}-\frac{2}{{k}} +\left(\frac{2}{{k}}-1.379\right)\right]\nonumber\\& =0.384\left|\frac{{e}\tilde{{E}}_{||}}{m{k}_{||}}\right|^{1/2}\left.\frac{\partial {f}_{0}}{\partial {v}_{||}}\right| _{{u}=0}\end{align}
Consequently, using
![]() ${\mathrm{d}v}_{||}={\mathrm{d}u}=|{e}\tilde{{E}}_{||}/{m}{{k}_{||}}|^{1/2}{\mathrm{d}j}$
yields
${\mathrm{d}v}_{||}={\mathrm{d}u}=|{e}\tilde{{E}}_{||}/{m}{{k}_{||}}|^{1/2}{\mathrm{d}j}$
yields
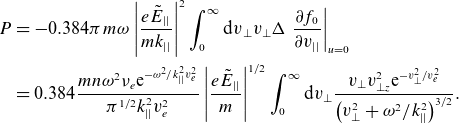 \begin{align}{P} & =-0.384\pi {m}\omega \left|\frac{{e}\tilde{{E}}_{\left| \right| }}{mk_{\left| \right| }}\right|^{2}\int _{0}^{{\infty }}{\mathrm{d}v}_{\bot }{v}_{\bot }\Delta \left.\frac{\partial {f}_{0}}{\partial v_{\left| \right| }}\right| _{u=0}\nonumber\\& =0.384\frac{{mn}{\omega ^{2}}\nu _{{e}}{\mathrm{e}}^{-{\omega ^{2}}/{k}_{||}^{2}{v}_{{e}}^{2}}}{\pi ^{1/2}k_{||}^{2}{v}_{{e}}^{2}}\left|\frac{{e}\tilde{{E}}_{||}}{{m}}\right|^{1/2}\int _{0}^{{\infty }}{\mathrm{d}v}_{\bot }\frac{{v}_{\bot }{v}_{\bot {z}}^{2}\mathrm{e}^{-{v}_{\bot }^{2}/{v}_{{e}}^{2}}}{\left({v}_{\bot }^{2}+\omega ^{2}/k_{||}^{2}\right)^{3/2}}.\end{align}
\begin{align}{P} & =-0.384\pi {m}\omega \left|\frac{{e}\tilde{{E}}_{\left| \right| }}{mk_{\left| \right| }}\right|^{2}\int _{0}^{{\infty }}{\mathrm{d}v}_{\bot }{v}_{\bot }\Delta \left.\frac{\partial {f}_{0}}{\partial v_{\left| \right| }}\right| _{u=0}\nonumber\\& =0.384\frac{{mn}{\omega ^{2}}\nu _{{e}}{\mathrm{e}}^{-{\omega ^{2}}/{k}_{||}^{2}{v}_{{e}}^{2}}}{\pi ^{1/2}k_{||}^{2}{v}_{{e}}^{2}}\left|\frac{{e}\tilde{{E}}_{||}}{{m}}\right|^{1/2}\int _{0}^{{\infty }}{\mathrm{d}v}_{\bot }\frac{{v}_{\bot }{v}_{\bot {z}}^{2}\mathrm{e}^{-{v}_{\bot }^{2}/{v}_{{e}}^{2}}}{\left({v}_{\bot }^{2}+\omega ^{2}/k_{||}^{2}\right)^{3/2}}.\end{align}
Recalling that the collision operator is valid for
![]() ${{x}^{2}}={v}^{2}/{v}_{{e}}^{2}\gg 1$
, while
${{x}^{2}}={v}^{2}/{v}_{{e}}^{2}\gg 1$
, while
![]() $\omega ^{2}/{k}_{||}^{2}{v}_{{e}}^{2}\approx 5/2\gg 1$
and
$\omega ^{2}/{k}_{||}^{2}{v}_{{e}}^{2}\approx 5/2\gg 1$
and
![]() ${v}_{\bot }^{2}\sim {v}_{{e}}^{2}$
, the resulting integral is approximately
${v}_{\bot }^{2}\sim {v}_{{e}}^{2}$
, the resulting integral is approximately
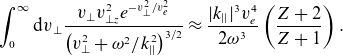 \begin{equation}\int _{0}^{{\infty }}{\mathrm{d}v}_{\bot }\frac{{v}_{\bot }{v}_{\bot {z}}^{2}e^{-{v}_{\bot }^{2}/{v}_{{e}}^{2}}}{\left({v}_{\bot }^{2}+\omega ^{2}/k_{||}^{2}\right)^{3/2}}\approx \frac{|k_{||}|^{3}{v}_{{e}}^{4}}{2\omega ^{3}}\left(\frac{Z+2}{Z+1}\right).\end{equation}
\begin{equation}\int _{0}^{{\infty }}{\mathrm{d}v}_{\bot }\frac{{v}_{\bot }{v}_{\bot {z}}^{2}e^{-{v}_{\bot }^{2}/{v}_{{e}}^{2}}}{\left({v}_{\bot }^{2}+\omega ^{2}/k_{||}^{2}\right)^{3/2}}\approx \frac{|k_{||}|^{3}{v}_{{e}}^{4}}{2\omega ^{3}}\left(\frac{Z+2}{Z+1}\right).\end{equation}
As a result, the RF power absorbed to drive the current for an intense applied lower hybrid wave is
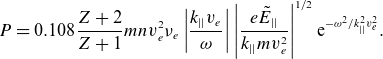 \begin{equation}{P}=0.108\frac{Z+2}{Z+1}{mnv}_{{e}}^{2}\nu _{{e}}\left|\frac{{k}_{||}{v}_{{e}}}{\omega }\right|\left|\frac{{e}\tilde{{E}}_{||}}{{k}_{||}{mv}_{{e}}^{2}}\right|^{1/2}{\mathrm{e}}^{-{\omega ^{2}}/{k}_{||}^{2}{v}_{{e}}^{2}}.\end{equation}
\begin{equation}{P}=0.108\frac{Z+2}{Z+1}{mnv}_{{e}}^{2}\nu _{{e}}\left|\frac{{k}_{||}{v}_{{e}}}{\omega }\right|\left|\frac{{e}\tilde{{E}}_{||}}{{k}_{||}{mv}_{{e}}^{2}}\right|^{1/2}{\mathrm{e}}^{-{\omega ^{2}}/{k}_{||}^{2}{v}_{{e}}^{2}}.\end{equation}
The driven current of (4.11) only depends on
![]() ${g}_{1}$
as seen by (4.4). It only depends on the reduced constant of the motion
${g}_{1}$
as seen by (4.4). It only depends on the reduced constant of the motion
![]() ${h}$
from (3.4). The form for
${h}$
from (3.4). The form for
![]() ${g}_{1}$
is constrained by the collision operator to satisfy (3.6), but the collision frequency does not enter. However, to drive current there must be dissipation. It enters through the power absorbed by the electrons from the applied lower hybrid wave. Collisions enter
${g}_{1}$
is constrained by the collision operator to satisfy (3.6), but the collision frequency does not enter. However, to drive current there must be dissipation. It enters through the power absorbed by the electrons from the applied lower hybrid wave. Collisions enter
![]() ${g}_{2}$
, as seen by (3.5), and it is required in (4.12).
${g}_{2}$
, as seen by (3.5), and it is required in (4.12).
Using
![]() $\nu _{{e}}=3\pi ^{1/2}({Z}+1)\nu _{{ee}}/4$
, the current drive efficiency in the intense field limit is
$\nu _{{e}}=3\pi ^{1/2}({Z}+1)\nu _{{ee}}/4$
, the current drive efficiency in the intense field limit is
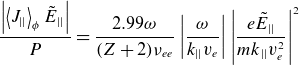 \begin{equation}\frac{\left|\left\langle {J}_{||}\right\rangle _{\phi }\tilde{{E}}_{||}\right|}{{P}}=\frac{2.99\omega }{(Z+2)\nu _{{ee}}}\left|\frac{\omega }{{k}_{||}{v}_{{e}}}\right|\left|\frac{{e}\tilde{{E}}_{||}}{{mk}_{||}{v}_{{e}}^{2}}\right|^{2}\end{equation}
\begin{equation}\frac{\left|\left\langle {J}_{||}\right\rangle _{\phi }\tilde{{E}}_{||}\right|}{{P}}=\frac{2.99\omega }{(Z+2)\nu _{{ee}}}\left|\frac{\omega }{{k}_{||}{v}_{{e}}}\right|\left|\frac{{e}\tilde{{E}}_{||}}{{mk}_{||}{v}_{{e}}^{2}}\right|^{2}\end{equation}
leading to the normalised form
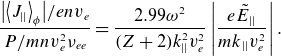 \begin{equation}\frac{\big|\big\langle {J}_{||}\big\rangle _{\phi }\big|/{env}_{{e}}}{{P}/{mnv}_{{e}}^{2}\nu _{{ee}}}=\frac{2.99\omega ^{2}}{({Z}+2){k}_{||}^{2}{v}_{{e}}^{2}}\left|\frac{{e}\tilde{{E}}_{||}}{{mk}_{||}{v}_{{e}}^{2}}\right|.\end{equation}
\begin{equation}\frac{\big|\big\langle {J}_{||}\big\rangle _{\phi }\big|/{env}_{{e}}}{{P}/{mnv}_{{e}}^{2}\nu _{{ee}}}=\frac{2.99\omega ^{2}}{({Z}+2){k}_{||}^{2}{v}_{{e}}^{2}}\left|\frac{{e}\tilde{{E}}_{||}}{{mk}_{||}{v}_{{e}}^{2}}\right|.\end{equation}
Ignoring aspect ratio modifications (Catto & Muni 2023) , the usual QL result (Fisch Reference Fisch1978) is
Both pitch angle and energy scatter matter in the intense field limit. Importantly, the intense field limit depends on
![]() $\tilde{{E}}_{||}$
, and is smaller by roughly
$\tilde{{E}}_{||}$
, and is smaller by roughly
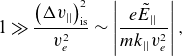 \begin{equation}1\gg \frac{\big(\Delta {v}_{||}\big)_{\mathrm{is}}^{2}}{{v}_{{e}}^{2}}\sim \left|\frac{{e}\tilde{{E}}_{||}}{{mk}_{||}{v}_{{e}}^{2}}\right|,\end{equation}
\begin{equation}1\gg \frac{\big(\Delta {v}_{||}\big)_{\mathrm{is}}^{2}}{{v}_{{e}}^{2}}\sim \left|\frac{{e}\tilde{{E}}_{||}}{{mk}_{||}{v}_{{e}}^{2}}\right|,\end{equation}
when
![]() $(\Delta {v}_{||})_{\mathrm{is}}^{2}\gg (\Delta {v}_{||})_{\nu }^{2}$
. Consequently, intense field LHCD is expected to be less efficient than QL predictions indicate. The result here, namely (4.19), as well as plasma edge turbulence likely explain some of the decrease in efficiency observed in experiments (Bonoli Reference Bonoli2014). The nonlinear reduction by
$(\Delta {v}_{||})_{\mathrm{is}}^{2}\gg (\Delta {v}_{||})_{\nu }^{2}$
. Consequently, intense field LHCD is expected to be less efficient than QL predictions indicate. The result here, namely (4.19), as well as plasma edge turbulence likely explain some of the decrease in efficiency observed in experiments (Bonoli Reference Bonoli2014). The nonlinear reduction by
![]() $(\Delta {v}_{||})_{\mathrm{is}}^{2}/{v}_{{e}}^{2}\ll 1$
occurs because the bound electrons are unable to carry current. The normalised efficiency is reduced, even though less power is absorbed in the narrow collisional boundary layers, because the bound region containing the non-current carrying electrons becomes much wider as the applied lower hybrid wave amplitude becomes larger. Additional island structures are expected to result in further reductions.
$(\Delta {v}_{||})_{\mathrm{is}}^{2}/{v}_{{e}}^{2}\ll 1$
occurs because the bound electrons are unable to carry current. The normalised efficiency is reduced, even though less power is absorbed in the narrow collisional boundary layers, because the bound region containing the non-current carrying electrons becomes much wider as the applied lower hybrid wave amplitude becomes larger. Additional island structures are expected to result in further reductions.
5. Discussion
It is normally assumed that a Maxwellian unperturbed distribution evolves due to QL effects generating non-Maxwellian features. However, the argument in § 1 indicates that these non-Maxwellian features should be taken as indication that a QL treatment is no longer valid and velocity space structure associated with island formation is starting to enter. As a result, the nonlinear term in the perturbed kinetic equation is no longer negligible and a full nonlinear solution is required. Interestingly, the unperturbed distribution remains nearly Maxwellian even in the presence of island formation and when the applied RF becomes intense as long as (4.21) is satisfied. In the intense limit collisional boundary layers form in very narrow regions about the separatrix and resolve the step function behaviour between the bound region and the two circulating regions. As only the circulating electrons can carry current and the island width is much larger than the collisional boundary layer width, less current is driven as indicated by comparing the intense field efficiency of (4.19) with the usual QL current drive efficiency of (4.20). This reduction in the efficiency offers at least a partial explanation of the experimentally observed decrease in current drive efficiency.
Note added in proofs. François Waelbroeck kindly brought to my attention a classic paper by Zakharov and Karpman (Reference Zakharov and Karpman1963) in which they demonstrate that Landau damping is a collisional process. The treatment in Catto (Reference Catto2025b) verifies their results by solving the steady state driven plasma wave problem linearly and nonlinearly with collisions. Details associated with the collision operator and the coefficient of the power absorbed in the weakly collisional, large plasma wave amplitude limit differ, but the procedure is broadly the same. Their pioneering treatment should be consulted for full details. Sugihara et al. (Reference Sugihara, Midzuno and Fukud1981) inappropriately modify the solution of Zakharov and Karpman (Reference Zakharov and Karpman1963) to remove the step function behavior at the collisional boundary layer enclosing the separatrix to obtain a piecewise continuous solution for the distribution function that no longer properly matches to the non-resonant electron distribution function (Catto 2025a). Their flawed result for the rf power absorbed agrees with the collisionless result of Canobbio (Reference Canobbio1972) as they note. The work here agrees with Zakharov and Karpman (Reference Zakharov and Karpman1963) within numerical coefficients associated with somewhat different forms for the collision operator.
Acknowledgements
The author is grateful to Miguel Calvo Carrera for the numerical evaluation of the integral C of (4.10). The United States Government retains a non-exclusive, paid-up, irrevocable, worldwide licence to publish or reproduce the published form of this paper, or allow others to do so, for United States Government purposes.
Editor Per Helander thanks the referees for their advice in evaluating this article.
Funding
This work was supported by the US Department of Energy under contract number DE-FG02-91ER-54109.
Declaration of interests
The author reports no conflict of interest.


