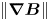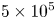1. Introduction
Stellarators can potentially provide steady-state plasma confinement with minimal recirculating power, passive stability and no danger of disruptions. However, stellarators require careful shaping of the field in order to confine trapped particles. This optimization is challenging because the space of plasma shapes is high-dimensional and known to contain multiple local minima (Bader et al. Reference Bader, Drevlak, Anderson, Faber, Hegna, Likin, Schmitt and Talmadge2019). Numerical optimization with local optimization algorithms is effective at finding individual configurations, but it does not provide a global picture of the space of solutions. Global optimization is difficult due to the high number of dimensions, and the dimensionality also makes parameter scans over the full space of possible shapes infeasible. Due to these challenges, it is not clear that all the interesting regions of parameter space have been found.
In this work, we attempt a global view of the space of optimized stellarators by using approximate magnetohydrodynamic (MHD) equilibria instead of full three-dimensional (3-D) equilibria, greatly reducing computational cost. In particular, we will use an expansion about the magnetic axis (Mercier Reference Mercier1964; Solovev & Shafranov Reference Solovev and Shafranov1970; Garren & Boozer Reference Garren and Boozer1991b), a closed field line representing the innermost flux surface. This expansion reduces the 3-D partial differential equations of MHD equilibrium to 1-D ordinary differential equations in the toroidal direction, lowering the time required to compute and diagnose a configuration by several orders of magnitude. It then becomes feasible to carry out high-resolution multi-dimensional parameter scans, resulting in large databases of stellarator configurations. While the expansion is approximate, it is necessarily accurate in the core (out to some minor radius) of any stellarator, even one for which the aspect ratio of the plasma boundary is low.
In this work we focus on the condition of quasisymmetry, one effective strategy for confining trapped particles (Boozer Reference Boozer1983; Nührenberg & Zille Reference Nührenberg and Zille1988; Helander Reference Helander2014). Quasisymmetry is a condition that the magnitude $B=|\boldsymbol{B}|$![]() of the magnetic field $\boldsymbol{B}$
of the magnetic field $\boldsymbol{B}$![]() is effectively two-dimensional instead of three-dimensional, with the continuous symmetry providing a conserved quantity that ensures confinement. Two types of quasisymmetry are possible near the axis: quasi-axisymmetry (QA), $B=B(r,\theta )$
is effectively two-dimensional instead of three-dimensional, with the continuous symmetry providing a conserved quantity that ensures confinement. Two types of quasisymmetry are possible near the axis: quasi-axisymmetry (QA), $B=B(r,\theta )$![]() , and quasi-helical symmetry (QH), $B=B(r, \theta - N\varphi )$
, and quasi-helical symmetry (QH), $B=B(r, \theta - N\varphi )$![]() . Here, $r$
. Here, $r$![]() is a flux surface label, $(\theta,\varphi )$
is a flux surface label, $(\theta,\varphi )$![]() are the Boozer poloidal and toroidal angles and $N$
are the Boozer poloidal and toroidal angles and $N$![]() is an integer. Although the weaker condition of omnigenity may be sufficient for trapped particle confinement, we focus here on quasisymmetry because the condition is easier to express mathematically, and since the omnigenous generalizations of QA and QH provide no extra freedom near the magnetic axis (Plunk, Landreman & Helander Reference Plunk, Landreman and Helander2019).
is an integer. Although the weaker condition of omnigenity may be sufficient for trapped particle confinement, we focus here on quasisymmetry because the condition is easier to express mathematically, and since the omnigenous generalizations of QA and QH provide no extra freedom near the magnetic axis (Plunk, Landreman & Helander Reference Plunk, Landreman and Helander2019).
In the first few orders of the near-axis expansion, it is possible to impose quasisymmetry directly, without optimization. Yet optimization is still useful, to maximize the minor radius over which the expansion is accurate. For most parameters of the near-axis model (which include the axis shape and a few other numbers), the minor radius over which the expansion is accurate is quite small. Therefore, the next-order terms in which quasisymmetry is broken are significant unless the plasma has extremely high aspect ratio, $> 10$![]() . By optimizing the parameters of the near-axis model, configurations can be obtained for which the expansion is accurate even at lower aspect ratios, in the range 5–10, typical of stellarator experiments. These configurations then have quasisymmetry over a significant volume. Since quasisymmetry is necessarily broken at third order in the expansion (Reference Garren and BoozerGarren & Boozer 1991a,Reference Garren and Boozerb), having good quasisymmetry over a large volume probably requires that the plasma be accurately described by the lower orders of the expansion (Rodriguez Reference Rodriguez2022).
. By optimizing the parameters of the near-axis model, configurations can be obtained for which the expansion is accurate even at lower aspect ratios, in the range 5–10, typical of stellarator experiments. These configurations then have quasisymmetry over a significant volume. Since quasisymmetry is necessarily broken at third order in the expansion (Reference Garren and BoozerGarren & Boozer 1991a,Reference Garren and Boozerb), having good quasisymmetry over a large volume probably requires that the plasma be accurately described by the lower orders of the expansion (Rodriguez Reference Rodriguez2022).
The method for generating stellarator configurations in this work is complementary to traditional stellarator optimization, in which the boundary shape of a finite-aspect-ratio plasma is the parameter space, and a fully 3-D MHD equilibrium code is run to evaluate the objective function. The method in this paper is necessarily approximate, but wider surveys over parameters are feasible. Conventional optimization is more accurate, but global optimization is more difficult. The two approaches could be used together, with the near-axis method identifying rough configurations that could be passed as an initial condition to conventional optimization for refinement.
Optimization has been applied to near-axis expansions in several previous publications. In Landreman & Sengupta (Reference Landreman and Sengupta2019), some results were shown from a preliminary version of the approach here, but the optimization method was not explained in detail. One purpose of the present article is to give a detailed presentation. A different approach for choosing parameters of the near-axis model and mapping the space of solutions was proposed in Rodriguez, Sengupta & Bhattacharjee (Reference Rodriguez, Sengupta and Bhattacharjee2022b). Optimization of a near-axis quasi-isodynamic (QI) stellarator was presented recently in Jorge et al. (Reference Jorge, Plunk, Drevlak, Landreman, Lobsien, Mata and Helander2022). Other optimizations of QI near-axis parameters are shown in Camacho Mata, Plunk & Jorge (Reference Camacho Mata, Plunk and Jorge2022).
The near-axis expansion for quasisymmetry has been discussed in detail in previous publications, but a brief review is given in § 2. In § 3, we describe the optimization problem for expanding the minor radius over which the expansion is accurate, and for achieving other desired physics properties. Next, a wide scan over parameters is presented in § 4, and the space of QA and QH configurations obtained is discussed. A few examples of configurations found in the scan are shown in § 5. We discuss the results and conclude in § 6.
2. Garren–Boozer expansion and diagnostics
Here, we give an overview of the near-axis expansion used for optimization, highlighting the quantities that are inputs and outputs for each stellarator configuration. We use the form of the expansion introduced by Reference Garren and BoozerGarren & Boozer (1991a,Reference Garren and Boozerb), in which the independent variables are Boozer coordinates. A detailed discussion can also be found in Landreman & Sengupta (Reference Landreman and Sengupta2019). This expansion has also been discussed in Landreman & Jorge (Reference Landreman and Jorge2020) and Landreman (Reference Landreman2021). There are other ways to carry out expansion about the axis in which the independent variables are not flux coordinates (Mercier Reference Mercier1964; Solovev & Shafranov Reference Solovev and Shafranov1970; Jorge, Sengupta & Landreman Reference Jorge, Sengupta and Landreman2020), which will not be considered here.
One input to the near-axis equations is the magnetic axis's shape. The position vector along the axis $\boldsymbol{r}_0$![]() can be expressed as a function of the arclength $\ell$
can be expressed as a function of the arclength $\ell$![]() along the curve. At each point on the axis, the Frenet frame is defined by
along the curve. At each point on the axis, the Frenet frame is defined by
Here, $(\boldsymbol{t},\boldsymbol{n},\boldsymbol{b})$![]() are the tangent, normal and binormal, a set of orthonormal vectors satisfying $\boldsymbol{t}\times \boldsymbol{n}=\boldsymbol{b}$
are the tangent, normal and binormal, a set of orthonormal vectors satisfying $\boldsymbol{t}\times \boldsymbol{n}=\boldsymbol{b}$![]() . Also, $\kappa$
. Also, $\kappa$![]() is the axis curvature, and $\tau$
is the axis curvature, and $\tau$![]() is the axis torsion. It can be shown that, for quasisymmetric configurations, $\kappa$
is the axis torsion. It can be shown that, for quasisymmetric configurations, $\kappa$![]() does not vanish, so the Frenet frame is well behaved.
does not vanish, so the Frenet frame is well behaved.
The position vector $\boldsymbol{r}$![]() of a general point (not necessarily on the axis) can then be written
of a general point (not necessarily on the axis) can then be written
where $r$![]() is a minor radius coordinate, $\varphi$
is a minor radius coordinate, $\varphi$![]() is a toroidal angle and $\vartheta$
is a toroidal angle and $\vartheta$![]() is another coordinate. We specifically define these three coordinates as follows. Letting $\psi$
is another coordinate. We specifically define these three coordinates as follows. Letting $\psi$![]() denote the toroidal flux divided by $2{\rm \pi}$
denote the toroidal flux divided by $2{\rm \pi}$![]() , an effective minor radius $r$
, an effective minor radius $r$![]() can be defined via $2{\rm \pi} |\psi | = {\rm \pi}r^2 B_0$
can be defined via $2{\rm \pi} |\psi | = {\rm \pi}r^2 B_0$![]() , where $B_0>0$
, where $B_0>0$![]() is the magnetic field strength on the axis, which is constant in quasisymmetry. Note that $r$
is the magnetic field strength on the axis, which is constant in quasisymmetry. Note that $r$![]() is a flux function, and not identical to the Euclidean distance to the axis or the magnitude of $\boldsymbol{r}$
is a flux function, and not identical to the Euclidean distance to the axis or the magnitude of $\boldsymbol{r}$![]() . We employ the poloidal and toroidal Boozer angles $\theta$
. We employ the poloidal and toroidal Boozer angles $\theta$![]() and $\varphi$
and $\varphi$![]() , in terms of which the field is
, in terms of which the field is
where $I$![]() and $G$
and $G$![]() are constant on flux surfaces. The remaining coordinate in (2.2) is defined as $\vartheta = \theta - N \varphi$
are constant on flux surfaces. The remaining coordinate in (2.2) is defined as $\vartheta = \theta - N \varphi$![]() , where $N$
, where $N$![]() is a constant integer, making $\vartheta$
is a constant integer, making $\vartheta$![]() a poloidal or helical angle for $N=0$
a poloidal or helical angle for $N=0$![]() and $N \ne 0$
and $N \ne 0$![]() , respectively. Defining $\iota _N = \iota - N$
, respectively. Defining $\iota _N = \iota - N$![]() , then
, then
We now consider $r$![]() to be small compared with length scales associated with the axis. In this case we can expand $X$
to be small compared with length scales associated with the axis. In this case we can expand $X$![]() , $Y$
, $Y$![]() and $Z$
and $Z$![]() in (2.2) as
in (2.2) as
Similar expansions hold for $Y$![]() and $Z$
and $Z$![]() . The field strength $B$
. The field strength $B$![]() and coefficient $\beta$
and coefficient $\beta$![]() can be expanded in the same way but with an $r^0$
can be expanded in the same way but with an $r^0$![]() term
term
Flux functions ($\iota$![]() , $G$
, $G$![]() , $I$
, $I$![]() and the pressure $p$
and the pressure $p$![]() ) must be even with respect to $r$
) must be even with respect to $r$![]() and so their expansions contain only even powers of $r$
and so their expansions contain only even powers of $r$![]()
The profile $I(r)$![]() is proportional to the toroidal current inside the flux surface, so $I_0 = 0$
is proportional to the toroidal current inside the flux surface, so $I_0 = 0$![]() .
.
Considerations of analyticity near the magnetic axis imply that poloidally varying quantities must have the form
(For a more detailed argument see Appendix A of Landreman & Sengupta Reference Landreman and Sengupta2018.) This same form applies also to $X$![]() , $Y$
, $Y$![]() , $Z$
, $Z$![]() and $\beta$
and $\beta$![]() .
.
So far, the position vector has been expressed as a power series in $r$![]() . Taking derivatives of this position vector with respect to the three coordinates, the dual relations (D'haeseleer et al. Reference D'haeseleer, Hitchon, Callen and Shohet2012) can then be used to evaluate $\boldsymbol {\nabla } \psi$
. Taking derivatives of this position vector with respect to the three coordinates, the dual relations (D'haeseleer et al. Reference D'haeseleer, Hitchon, Callen and Shohet2012) can then be used to evaluate $\boldsymbol {\nabla } \psi$![]() , $\boldsymbol {\nabla } \vartheta$
, $\boldsymbol {\nabla } \vartheta$![]() , and $\boldsymbol {\nabla } \varphi$
, and $\boldsymbol {\nabla } \varphi$![]() . The results are substituted into (2.4) and (2.5). Equating these covariant and contravariant forms of $\boldsymbol{B}$
. The results are substituted into (2.4) and (2.5). Equating these covariant and contravariant forms of $\boldsymbol{B}$![]() , powers of $r$
, powers of $r$![]() can be collected at each order. Moreover, the inner product (2.4)$\cdot$
can be collected at each order. Moreover, the inner product (2.4)$\cdot$![]() (2.5) yields an expression for the field strength, $B^2/(G+\iota I) = \boldsymbol {\nabla } \psi \boldsymbol{\cdot }\boldsymbol {\nabla } \vartheta \times \boldsymbol {\nabla } \varphi$
(2.5) yields an expression for the field strength, $B^2/(G+\iota I) = \boldsymbol {\nabla } \psi \boldsymbol{\cdot }\boldsymbol {\nabla } \vartheta \times \boldsymbol {\nabla } \varphi$![]() , providing an additional equation at each order in $r$
, providing an additional equation at each order in $r$![]() . One more equation is provided by MHD equilibrium, $(\boldsymbol {\nabla } \times \boldsymbol{B})\times \boldsymbol{B} = \mu _0\boldsymbol {\nabla } p$
. One more equation is provided by MHD equilibrium, $(\boldsymbol {\nabla } \times \boldsymbol{B})\times \boldsymbol{B} = \mu _0\boldsymbol {\nabla } p$![]() . Here, only the $\boldsymbol {\nabla } \psi$
. Here, only the $\boldsymbol {\nabla } \psi$![]() component provides new information. Finally, if quasisymmetry is desired, the condition $B = B(\psi, \vartheta )$
component provides new information. Finally, if quasisymmetry is desired, the condition $B = B(\psi, \vartheta )$![]() can be imposed. These conditions provide an increasing number of constraints at each order in $r$
can be imposed. These conditions provide an increasing number of constraints at each order in $r$![]() .
.
The conditions obtained at each order are now summarized, for the case of quasisymmetry. At leading order, $B_0$![]() is independent of $\varphi$
is independent of $\varphi$![]() . It is also determined that $\varphi = 2{\rm \pi} \ell / L$
. It is also determined that $\varphi = 2{\rm \pi} \ell / L$![]() and $|G_0|=B_0 L/(2{\rm \pi} )$
and $|G_0|=B_0 L/(2{\rm \pi} )$![]() , where $L$
, where $L$![]() is the axis length. While $B_0$
is the axis length. While $B_0$![]() can be considered an input parameter, it merely scales the field strength of the configuration and so does not provide true flexibility. At next order, $B_{1s}$
can be considered an input parameter, it merely scales the field strength of the configuration and so does not provide true flexibility. At next order, $B_{1s}$![]() can be set to zero using the freedom in the origin of $\vartheta$
can be set to zero using the freedom in the origin of $\vartheta$![]() , and $B_{1c}$
, and $B_{1c}$![]() must be independent of $\varphi$
must be independent of $\varphi$![]() . Following Garren & Boozer (Reference Garren and Boozer1991b) we use the constant $\bar {\eta }=B_{1c}/B_0$
. Following Garren & Boozer (Reference Garren and Boozer1991b) we use the constant $\bar {\eta }=B_{1c}/B_0$![]() . The quantity $\bar {\eta }$
. The quantity $\bar {\eta }$![]() thus controls how much $B$
thus controls how much $B$![]() varies on a flux surface of given minor radius, via
varies on a flux surface of given minor radius, via
We consider $\bar {\eta }$![]() to be another input of the calculation. Also, it can be shown that $N$
to be another input of the calculation. Also, it can be shown that $N$![]() must equal the number of times the axis normal vector rotates poloidally about the axis as the axis is traversed toroidally. Typically $|N|$
must equal the number of times the axis normal vector rotates poloidally about the axis as the axis is traversed toroidally. Typically $|N|$![]() equals either 0 or the number of field periods $n_{\mathrm {fp}}$
equals either 0 or the number of field periods $n_{\mathrm {fp}}$![]() , as is the case for all configurations found in this work, though other values of $N$
, as is the case for all configurations found in this work, though other values of $N$![]() are allowed as well.
are allowed as well.
A key constraint at this order is a Ricatti equation, (2.14) in Landreman & Sengupta (Reference Landreman and Sengupta2019), an ordinary differential equation (ODE) in $\varphi$![]() . This equation relates $\kappa$
. This equation relates $\kappa$![]() , $\tau$
, $\tau$![]() , $\iota _0$
, $\iota _0$![]() , $I_2$
, $I_2$![]() , $\bar {\eta }$
, $\bar {\eta }$![]() and the $O(r)$
and the $O(r)$![]() flux surface shapes. As discussed in the appendix of Landreman, Sengupta & Plunk (Reference Landreman, Sengupta and Plunk2019), it is convenient to consider as inputs $I_2$
flux surface shapes. As discussed in the appendix of Landreman, Sengupta & Plunk (Reference Landreman, Sengupta and Plunk2019), it is convenient to consider as inputs $I_2$![]() and the deviation from stellarator symmetry at $\varphi =0$
and the deviation from stellarator symmetry at $\varphi =0$![]() , in which case there is a unique solution for $\iota _0$
, in which case there is a unique solution for $\iota _0$![]() and the first-order surface shape. Alternatively, $\iota _0$
and the first-order surface shape. Alternatively, $\iota _0$![]() could be considered the input and $I_2$
could be considered the input and $I_2$![]() the output (Rodríguez, Sengupta & Bhattacharjee Reference Rodríguez, Sengupta and Bhattacharjee2022c), but we will not do this here. For all work in this paper we assume stellarator symmetry and no current density on the axis, $I_2=0$
the output (Rodríguez, Sengupta & Bhattacharjee Reference Rodríguez, Sengupta and Bhattacharjee2022c), but we will not do this here. For all work in this paper we assume stellarator symmetry and no current density on the axis, $I_2=0$![]() . (To include $I_2$
. (To include $I_2$![]() and non-stellarator-symmetric configurations, no substantial changes to the methods in this paper would be required.) Therefore there are no inputs to the model other than $\bar {\eta }$
and non-stellarator-symmetric configurations, no substantial changes to the methods in this paper would be required.) Therefore there are no inputs to the model other than $\bar {\eta }$![]() at this order. At this order, the flux surface shapes are rotated ellipses (in the plane perpendicular to the magnetic axis) centred on the axis. Generally the elongation varies with $\varphi$
at this order. At this order, the flux surface shapes are rotated ellipses (in the plane perpendicular to the magnetic axis) centred on the axis. Generally the elongation varies with $\varphi$![]() .
.
Proceeding to next order in $r$![]() , it was found by Garren & Boozer (Reference Garren and Boozer1991b) that it is not possible to fully specify $B_2$
, it was found by Garren & Boozer (Reference Garren and Boozer1991b) that it is not possible to fully specify $B_2$![]() for a general axis shape, meaning it is not possible to achieve quasisymmetry at this order for most axis shapes. To handle this complication we proceed as in Landreman & Sengupta (Reference Landreman and Sengupta2019), only partially imposing quasisymmetry at this order. Specifically, we treat $B_{2c}$
for a general axis shape, meaning it is not possible to achieve quasisymmetry at this order for most axis shapes. To handle this complication we proceed as in Landreman & Sengupta (Reference Landreman and Sengupta2019), only partially imposing quasisymmetry at this order. Specifically, we treat $B_{2c}$![]() and $B_{2s}$
and $B_{2s}$![]() as inputs, but consider $B_{20}$
as inputs, but consider $B_{20}$![]() an output. For stellarator symmetry, $B_{2s}=0$
an output. For stellarator symmetry, $B_{2s}=0$![]() , so this quantity will not be considered further here. For quasisymmetry, $B_{2c}$
, so this quantity will not be considered further here. For quasisymmetry, $B_{2c}$![]() is constant (independent of $\varphi$
is constant (independent of $\varphi$![]() ), providing one more scalar input parameter. Then, $B_{20}(\varphi )$
), providing one more scalar input parameter. Then, $B_{20}(\varphi )$![]() can be computed from a linear system of ODEs. These equations and the surface shapes depend on $p_2$
can be computed from a linear system of ODEs. These equations and the surface shapes depend on $p_2$![]() , representing the leading behaviour of the pressure near the axis. The flux surface shapes at this order include triangularity and Shafranov shift.
, representing the leading behaviour of the pressure near the axis. The flux surface shapes at this order include triangularity and Shafranov shift.
It is possible to consider higher-order terms in the expansion. However, we stop here, at $O(r^2)$![]() , for all results in this paper. This order is sufficient for representing realistic stellarator shapes. If one were to proceed to higher order, quasisymmetry cannot be fully imposed, and choices would need to be made for other functions of toroidal angle, which significantly increases the number of parameters in the model. Note also that, in an asymptotic expansion such as this one, including higher-order terms may decrease rather than increase accuracy.
, for all results in this paper. This order is sufficient for representing realistic stellarator shapes. If one were to proceed to higher order, quasisymmetry cannot be fully imposed, and choices would need to be made for other functions of toroidal angle, which significantly increases the number of parameters in the model. Note also that, in an asymptotic expansion such as this one, including higher-order terms may decrease rather than increase accuracy.
To summarize, at the order of interest, the inputs to the near-axis equations are the shape of the axis and the three scalar parameters $\bar {\eta }$![]() , $B_{2c}$
, $B_{2c}$![]() and $p_2$
and $p_2$![]() . The outputs of the model include $\iota _0$
. The outputs of the model include $\iota _0$![]() , $B_{20}$
, $B_{20}$![]() and a parameterization of all flux surface shapes in a neighbourhood of the axis. An efficient numerical method for solving the ODEs to this order is detailed in § 4.2 of Landreman & Sengupta (Reference Landreman and Sengupta2019), which we also adopt in this work. Since the shapes of the flux surfaces are known, any one surface can be used as the input to a standard fixed-boundary 3-D MHD equilibrium calculation that does not make a near-axis expansion. From the result, other standard stellarator codes can be run to check the accuracy of the near-axis approximations and to evaluate other physics properties. Examples of this procedure can be seen in Landreman et al. (Reference Landreman, Sengupta and Plunk2019), Landreman & Sengupta (Reference Landreman and Sengupta2019) and Jorge et al. (Reference Jorge, Plunk, Drevlak, Landreman, Lobsien, Mata and Helander2022).
and a parameterization of all flux surface shapes in a neighbourhood of the axis. An efficient numerical method for solving the ODEs to this order is detailed in § 4.2 of Landreman & Sengupta (Reference Landreman and Sengupta2019), which we also adopt in this work. Since the shapes of the flux surfaces are known, any one surface can be used as the input to a standard fixed-boundary 3-D MHD equilibrium calculation that does not make a near-axis expansion. From the result, other standard stellarator codes can be run to check the accuracy of the near-axis approximations and to evaluate other physics properties. Examples of this procedure can be seen in Landreman et al. (Reference Landreman, Sengupta and Plunk2019), Landreman & Sengupta (Reference Landreman and Sengupta2019) and Jorge et al. (Reference Jorge, Plunk, Drevlak, Landreman, Lobsien, Mata and Helander2022).
Once these near-axis equations are solved for the configuration geometry, some quantities of interest are known immediately, such as $\iota _0$![]() and the quasisymmetry error associated with variation of $B_{20}$
and the quasisymmetry error associated with variation of $B_{20}$![]() . Many other quantities of interest can be computed directly from the solution at negligible computational cost. One example (Landreman & Jorge Reference Landreman and Jorge2020) is the vacuum magnetic well $\textrm {d}^2 V /\textrm {d} \psi ^2$
. Many other quantities of interest can be computed directly from the solution at negligible computational cost. One example (Landreman & Jorge Reference Landreman and Jorge2020) is the vacuum magnetic well $\textrm {d}^2 V /\textrm {d} \psi ^2$![]() , where $V(\psi )$
, where $V(\psi )$![]() is the flux surface volume. Another is the Mercier stability criterion $D_{\mathrm {Merc}}$
is the flux surface volume. Another is the Mercier stability criterion $D_{\mathrm {Merc}}$![]() .
.
From a solution of the near-axis equations, it is also possible to directly compute all the geometric quantities appearing in the gyrokinetic equation and the MHD ballooning equation (Jorge & Landreman Reference Jorge and Landreman2021). However, this information will not be exploited here.
Other quantities that can be computed include measures for the minor radius over which the expansion is accurate. A precise measure of this radius has not yet been decisively identified, but several estimates have been suggested. Here, we will use three estimates. The first two of these are scale lengths associated with the first and second derivatives of the magnetic field vector (Landreman Reference Landreman2021)
Here, $|| \cdots ||$![]() indicates the square root of the sum of the squares of the elements of the matrix or tensor. In the case of a matrix this is the Frobenius norm. The quantities $L_{\boldsymbol {\nabla } B}$
indicates the square root of the sum of the squares of the elements of the matrix or tensor. In the case of a matrix this is the Frobenius norm. The quantities $L_{\boldsymbol {\nabla } B}$![]() and $L_{\boldsymbol {\nabla } \boldsymbol {\nabla } B}$
and $L_{\boldsymbol {\nabla } \boldsymbol {\nabla } B}$![]() have dimensions of length, and are each normalized so that in the case of an infinite straight wire, they give the distance to the wire. The near-axis expansion is expected to be accurate only if the distance to the axis is small compared with scale lengths in the magnetic field, i.e. for $r \ll L_{\boldsymbol {\nabla } B}$
have dimensions of length, and are each normalized so that in the case of an infinite straight wire, they give the distance to the wire. The near-axis expansion is expected to be accurate only if the distance to the axis is small compared with scale lengths in the magnetic field, i.e. for $r \ll L_{\boldsymbol {\nabla } B}$![]() and $r \ll L_{\boldsymbol {\nabla } \boldsymbol {\nabla } B}$
and $r \ll L_{\boldsymbol {\nabla } \boldsymbol {\nabla } B}$![]() . Therefore, it is desirable to maximize these two quantities. Another estimate for the radius over which the expansion is accurate is $r_c$
. Therefore, it is desirable to maximize these two quantities. Another estimate for the radius over which the expansion is accurate is $r_c$![]() , defined in § 4 of Landreman (Reference Landreman2021). This quantity is the maximum minor radius at which the second-order flux surface shapes are no longer smooth and nested. The near-axis expansion has necessarily broken down when $r$
, defined in § 4 of Landreman (Reference Landreman2021). This quantity is the maximum minor radius at which the second-order flux surface shapes are no longer smooth and nested. The near-axis expansion has necessarily broken down when $r$![]() is as large as $r_c$
is as large as $r_c$![]() , so $r_c$
, so $r_c$![]() is a natural target for maximization.
is a natural target for maximization.
This near-axis model has a limitation related to the bootstrap current. To the order in $r$![]() considered here, the current profile has only a single degree of freedom, $I_2$
considered here, the current profile has only a single degree of freedom, $I_2$![]() , corresponding to a current density that is independent of $r$
, corresponding to a current density that is independent of $r$![]() . However, realistic bootstrap current profiles are peaked at mid-radius, going to zero on axis where the pressure gradient vanishes, and also becoming small at the plasma edge where the collisionality becomes large. Therefore it is not possible to represent realistic profile shapes of bootstrap current in the near-axis model used here. Throughout this paper we proceed by choosing $I_2=0$
. However, realistic bootstrap current profiles are peaked at mid-radius, going to zero on axis where the pressure gradient vanishes, and also becoming small at the plasma edge where the collisionality becomes large. Therefore it is not possible to represent realistic profile shapes of bootstrap current in the near-axis model used here. Throughout this paper we proceed by choosing $I_2=0$![]() , consistent with the bootstrap current vanishing on the magnetic axis. However, important questions for future research are whether the near-axis model can be extended to higher order to incorporate realistic current profile shapes, and whether it is a reasonable approximation to make $I_2$
, consistent with the bootstrap current vanishing on the magnetic axis. However, important questions for future research are whether the near-axis model can be extended to higher order to incorporate realistic current profile shapes, and whether it is a reasonable approximation to make $I_2$![]() equal to a radial average of the current profile.
equal to a radial average of the current profile.
3. Optimization problem
The motivation for optimization of the near-axis parameters can be seen in figure 1. The left panel shows a cross-section of flux surfaces computed by the near-axis model for unoptimized input parameters: an axis shape $R(\phi )=1-0.12\cos (2\phi )$![]() and $Z(\phi )=0.12\cos (2\phi )$
and $Z(\phi )=0.12\cos (2\phi )$![]() , $\bar {\eta }=-0.7$
, $\bar {\eta }=-0.7$![]() and $B_{2c}=-0.5$
and $B_{2c}=-0.5$![]() . It can be seen that the region of smooth and nested flux surfaces is small, limiting the configuration to very high aspect ratio. For comparison, the right panel of figure 1 shows an optimized near-axis configuration on the same scale. (This configuration will be described in detail in § 5.1). It can be seen that the region of smooth nested surfaces extends to much lower aspect ratio, beyond the range shown. Thus, although quasisymmetry can be imposed directly in the near-axis equations (to $O(r)$
. It can be seen that the region of smooth and nested flux surfaces is small, limiting the configuration to very high aspect ratio. For comparison, the right panel of figure 1 shows an optimized near-axis configuration on the same scale. (This configuration will be described in detail in § 5.1). It can be seen that the region of smooth nested surfaces extends to much lower aspect ratio, beyond the range shown. Thus, although quasisymmetry can be imposed directly in the near-axis equations (to $O(r)$![]() ), optimization is still valuable. Optimization is also useful for achieving quasisymmetry fully through $O(r^2)$
), optimization is still valuable. Optimization is also useful for achieving quasisymmetry fully through $O(r^2)$![]() since, as mentioned above, for general input parameters $B_{20}$
since, as mentioned above, for general input parameters $B_{20}$![]() will depend on $\varphi$
will depend on $\varphi$![]() .
.

Figure 1. (a) Generic $O(r^2)$![]() near-axis configurations tend to be limited to very high aspect ratio before the predicted surface shapes are self-intersecting or non-nested. (b) By optimizing the axis shape, $\bar {\eta }$
near-axis configurations tend to be limited to very high aspect ratio before the predicted surface shapes are self-intersecting or non-nested. (b) By optimizing the axis shape, $\bar {\eta }$![]() and $B_{2c}$
and $B_{2c}$![]() , the volume of smooth nested surfaces can be dramatically increased. Surfaces shown are $r=0.02, 0.04, \ldots, 0.12$
, the volume of smooth nested surfaces can be dramatically increased. Surfaces shown are $r=0.02, 0.04, \ldots, 0.12$![]() m on the left and $r=0.02, 0.04, \ldots, 0.2$
m on the left and $r=0.02, 0.04, \ldots, 0.2$![]() m on the right.
m on the right.
Let us now present the details of an optimization problem that is effective for the near-axis quasisymmetry equations. The axis shape is represented in cylindrical coordinates $(R,\phi,Z)$![]() using finite Fourier series
using finite Fourier series

where $n_{\mathrm {fp}}$![]() is the number of field periods, and a finite maximum Fourier number $N_F$
is the number of field periods, and a finite maximum Fourier number $N_F$![]() has been chosen. Stellarator symmetry has been assumed. Some axis shapes cannot be represented using (3.1a,b): those for which $\phi$
has been chosen. Stellarator symmetry has been assumed. Some axis shapes cannot be represented using (3.1a,b): those for which $\phi$![]() is not monotonic, or those which encircle the $Z$
is not monotonic, or those which encircle the $Z$![]() axis more than once. However, the choice (3.1a,b) describes every stellarator experiment to date and so is convenient for this initial study. The parameter space for optimization consists of $\{R_n, Z_n, \bar {\eta }, B_{2c} \}$
axis more than once. However, the choice (3.1a,b) describes every stellarator experiment to date and so is convenient for this initial study. The parameter space for optimization consists of $\{R_n, Z_n, \bar {\eta }, B_{2c} \}$![]() . The mode $R_0$
. The mode $R_0$![]() is set to 1 and excluded from the parameter space so that the average major radius is held fixed.
is set to 1 and excluded from the parameter space so that the average major radius is held fixed.
The objective function considered is a sum of terms
where the scalars $w_j$![]() are weights used to vary the emphasis on the different terms. The individual terms are
are weights used to vary the emphasis on the different terms. The individual terms are

Here, $L$![]() is the length of the magnetic axis, $\int \, \textrm {d} \ell$
is the length of the magnetic axis, $\int \, \textrm {d} \ell$![]() indicates an integral over the axis and quantities with a subscript $*$
indicates an integral over the axis and quantities with a subscript $*$![]() indicate specified target values. The motivation for these terms is as follows.
indicate specified target values. The motivation for these terms is as follows.
Minimizing $f_{\boldsymbol {\nabla } }$![]() increases $L_{\boldsymbol {\nabla } B}$
increases $L_{\boldsymbol {\nabla } B}$![]() , which in practice is found to expand the radius of good quasisymmetry. The term $f_{\boldsymbol {\nabla } }$
, which in practice is found to expand the radius of good quasisymmetry. The term $f_{\boldsymbol {\nabla } }$![]() is the most effective term for this purpose based on experience so far. Similarly, minimizing $f_{\boldsymbol {\nabla } \boldsymbol {\nabla } }$
is the most effective term for this purpose based on experience so far. Similarly, minimizing $f_{\boldsymbol {\nabla } \boldsymbol {\nabla } }$![]() increases the radius of good quasisymmetry by increasing $L_{\boldsymbol {\nabla } \boldsymbol {\nabla } B}$
increases the radius of good quasisymmetry by increasing $L_{\boldsymbol {\nabla } \boldsymbol {\nabla } B}$![]() . Note that the term $f_{\boldsymbol {\nabla } }$
. Note that the term $f_{\boldsymbol {\nabla } }$![]() does not depend on the second-order solution at all, so it does not directly constrain $B_{2c}$
does not depend on the second-order solution at all, so it does not directly constrain $B_{2c}$![]() .
.
The term $f_L$![]() is included to avoid a problem that otherwise occurs when the initial axis shape is consistent with QH (i.e. the normal vector makes complete poloidal rotations as the axis is followed toroidally). In this case, the optimizer can reduce $f_{\boldsymbol {\nabla }}$
is included to avoid a problem that otherwise occurs when the initial axis shape is consistent with QH (i.e. the normal vector makes complete poloidal rotations as the axis is followed toroidally). In this case, the optimizer can reduce $f_{\boldsymbol {\nabla }}$![]() by making the helical excursion of the magnetic axis as large as the major radius, so $R$
by making the helical excursion of the magnetic axis as large as the major radius, so $R$![]() drops to 0 every field period. This state is unacceptable, since adequate space is required in the middle of the torus for the electromagnetic coils and other components. By including $f_L$
drops to 0 every field period. This state is unacceptable, since adequate space is required in the middle of the torus for the electromagnetic coils and other components. By including $f_L$![]() in the objective, this problem is avoided. An objective term that penalizes values of $R$
in the objective, this problem is avoided. An objective term that penalizes values of $R$![]() below a threshold was also considered to avoid this pathology. However, $f_L$
below a threshold was also considered to avoid this pathology. However, $f_L$![]() has produced better optima in practice. Through different choices of $L_*$
has produced better optima in practice. Through different choices of $L_*$![]() , the user can parameterize a family of configurations in which there is a trade-off between the quality of quasisymmetry versus space in the middle of the torus.
, the user can parameterize a family of configurations in which there is a trade-off between the quality of quasisymmetry versus space in the middle of the torus.
Similarly, the term $f_\iota$![]() is included to avoid a problem that otherwise occurs when the initial axis shape is consistent with QA (i.e. the normal vector does not make any complete poloidal rotations as the axis is followed toroidally). In this case, the optimizer can reduce $f_{\boldsymbol {\nabla }}$
is included to avoid a problem that otherwise occurs when the initial axis shape is consistent with QA (i.e. the normal vector does not make any complete poloidal rotations as the axis is followed toroidally). In this case, the optimizer can reduce $f_{\boldsymbol {\nabla }}$![]() by making the axis axisymmetric. Including $f_\iota$
by making the axis axisymmetric. Including $f_\iota$![]() in the objective with a non-zero value of $\iota _*$
in the objective with a non-zero value of $\iota _*$![]() cures this problem. Because $f_L$
cures this problem. Because $f_L$![]() and $f_\iota$
and $f_\iota$![]() are useful for QH and QA symmetry, respectively, we set $w_L=0$
are useful for QH and QA symmetry, respectively, we set $w_L=0$![]() when seeking QA configurations and set $w_\iota =0$
when seeking QA configurations and set $w_\iota =0$![]() when seeking QH configurations.
when seeking QH configurations.
Minimizing the term $f_{B2}$![]() makes $B_{20}$
makes $B_{20}$![]() (nearly) independent of $\varphi$
(nearly) independent of $\varphi$![]() . This makes the near-axis solution fully quasisymmetric through second order in $r$
. This makes the near-axis solution fully quasisymmetric through second order in $r$![]() .
.
Although we in principle wish to maximize $r_c$![]() , the minor radius at which the second-order surfaces become singular, we find it not very effective in practice to directly optimize functions of $r_c$
, the minor radius at which the second-order surfaces become singular, we find it not very effective in practice to directly optimize functions of $r_c$![]() . A possible reason for this can be understood from figure 2. The horizontal coordinate $\lambda$
. A possible reason for this can be understood from figure 2. The horizontal coordinate $\lambda$![]() in this figure indicates an interpolation between the optimized QH configuration of § 5.4 of Landreman & Sengupta (Reference Landreman and Sengupta2019), corresponding to $\lambda =1$
in this figure indicates an interpolation between the optimized QH configuration of § 5.4 of Landreman & Sengupta (Reference Landreman and Sengupta2019), corresponding to $\lambda =1$![]() , and a typical initial condition, corresponding to $\lambda =0$
, and a typical initial condition, corresponding to $\lambda =0$![]() . Letting a subscript * denote values for the optimized configuration, the parameters for the intermediate configurations are $R_n = \lambda R_{n*}$
. Letting a subscript * denote values for the optimized configuration, the parameters for the intermediate configurations are $R_n = \lambda R_{n*}$![]() and $Z_n=\lambda Z_{n*}$
and $Z_n=\lambda Z_{n*}$![]() for $n>1$
for $n>1$![]() , $R_n=R_{n*}$
, $R_n=R_{n*}$![]() and $Z_n=Z_{n*}$
and $Z_n=Z_{n*}$![]() for $n \le 1$
for $n \le 1$![]() , $\bar {\eta } = 1 + \lambda (\bar {\eta }_* - 1)$
, $\bar {\eta } = 1 + \lambda (\bar {\eta }_* - 1)$![]() and $B_{2c}=\lambda B_{2c*}$
and $B_{2c}=\lambda B_{2c*}$![]() . Therefore, as $\lambda$
. Therefore, as $\lambda$![]() decreases from 1 to 0, the configuration is smoothly interpolated to one with simplified parameters, such as only Fourier modes with $n =0$
decreases from 1 to 0, the configuration is smoothly interpolated to one with simplified parameters, such as only Fourier modes with $n =0$![]() or 1 in the axis shape. In optimization, one typically moves in the opposite direction, starting with an initial guess like the $\lambda =0$
or 1 in the axis shape. In optimization, one typically moves in the opposite direction, starting with an initial guess like the $\lambda =0$![]() case, and aiming to end up at a configuration like the $\lambda =1$
case, and aiming to end up at a configuration like the $\lambda =1$![]() case. It can be seen in figure 2 that $R_0/r_c$
case. It can be seen in figure 2 that $R_0/r_c$![]() is not monotonic along this path. Due to the ‘barrier’ in between, it is hard to get from the $\lambda =0$
is not monotonic along this path. Due to the ‘barrier’ in between, it is hard to get from the $\lambda =0$![]() initial condition to the $\lambda =1$
initial condition to the $\lambda =1$![]() optimized configuration using the objective $R_0/r_c$
optimized configuration using the objective $R_0/r_c$![]() , even though the final value of $R_0/r_c$
, even though the final value of $R_0/r_c$![]() at $\lambda =1$
at $\lambda =1$![]() is favourable. In contrast, the figure shows that $f_{\boldsymbol {\nabla }}$
is favourable. In contrast, the figure shows that $f_{\boldsymbol {\nabla }}$![]() is monotonically decreasing with $\lambda$
is monotonically decreasing with $\lambda$![]() , making it an effective objective function. In short, although minimizing the aspect ratio $R_0/r_c$
, making it an effective objective function. In short, although minimizing the aspect ratio $R_0/r_c$![]() is an intuitive goal, it turns out that directly applying minimization to $R_0/r_c$
is an intuitive goal, it turns out that directly applying minimization to $R_0/r_c$![]() is less effective than minimizing the better-behaved function $f_{\boldsymbol {\nabla }}$
is less effective than minimizing the better-behaved function $f_{\boldsymbol {\nabla }}$![]() .
.

Figure 2. Variation of several possible objective function terms as one interpolates between the optimized QH configuration of Landreman & Sengupta (Reference Landreman and Sengupta2019) ($\lambda =1$![]() ) and a typical initial condition ($\lambda =0$
) and a typical initial condition ($\lambda =0$![]() ) defined by $R_n=Z_n=0$
) defined by $R_n=Z_n=0$![]() for $n>1$
for $n>1$![]() , $\bar {\eta }=1$
, $\bar {\eta }=1$![]() and $B_{2c}=0$
and $B_{2c}=0$![]() . The objective $f_{\boldsymbol {\nabla }}$
. The objective $f_{\boldsymbol {\nabla }}$![]() is most useful because it varies between these configurations monotonically. The other terms shown increase with $\lambda$
is most useful because it varies between these configurations monotonically. The other terms shown increase with $\lambda$![]() before they decrease, making it hard to get from $\lambda =0$
before they decrease, making it hard to get from $\lambda =0$![]() to $\lambda =1$
to $\lambda =1$![]() when they dominate the objective.
when they dominate the objective.
Figure 2 also shows the function $f_{\boldsymbol {\nabla } \boldsymbol {\nabla } }$![]() has a similar non-monotonic behaviour to $R_0/r_c$
has a similar non-monotonic behaviour to $R_0/r_c$![]() , so $f_{\boldsymbol {\nabla } \boldsymbol {\nabla }}$
, so $f_{\boldsymbol {\nabla } \boldsymbol {\nabla }}$![]() is ineffective if used as the dominant term in the objective function. However, adding a small multiple of $f_{\boldsymbol {\nabla } \boldsymbol {\nabla } }$
is ineffective if used as the dominant term in the objective function. However, adding a small multiple of $f_{\boldsymbol {\nabla } \boldsymbol {\nabla } }$![]() or $R_0/r_c$
or $R_0/r_c$![]() to $f_{\boldsymbol {\nabla }}$
to $f_{\boldsymbol {\nabla }}$![]() can still be effective. Other potential objective functions were also explored based on $X_2$
can still be effective. Other potential objective functions were also explored based on $X_2$![]() , $Y_2$
, $Y_2$![]() and their $\textrm {d}/\textrm {d}\varphi$
and their $\textrm {d}/\textrm {d}\varphi$![]() derivatives. These quantities were found to have non-monotonic behaviour similar to the right two panels of figure 2. A possible explanation for the different monotonic vs non-monotonic behaviour of the various objective function terms might be the following. Both $f_{\boldsymbol {\nabla } \boldsymbol {\nabla } }$
derivatives. These quantities were found to have non-monotonic behaviour similar to the right two panels of figure 2. A possible explanation for the different monotonic vs non-monotonic behaviour of the various objective function terms might be the following. Both $f_{\boldsymbol {\nabla } \boldsymbol {\nabla } }$![]() and $R_0/r_c$
and $R_0/r_c$![]() depend on $O(r^2)$
depend on $O(r^2)$![]() quantities whereas $f_{\boldsymbol {\nabla } }$
quantities whereas $f_{\boldsymbol {\nabla } }$![]() depends only on $O(r^1)$
depends only on $O(r^1)$![]() quantities, and the $O(r^2)$
quantities, and the $O(r^2)$![]() quantities are more sensitive to small changes in the axis shape due to $\textrm {d}/\textrm {d}\varphi$
quantities are more sensitive to small changes in the axis shape due to $\textrm {d}/\textrm {d}\varphi$![]() derivatives in the near-axis equations. In practice, the most effective approach to lower the aspect ratio seems to be using an objective dominated by $f_{\boldsymbol {\nabla }}$
derivatives in the near-axis equations. In practice, the most effective approach to lower the aspect ratio seems to be using an objective dominated by $f_{\boldsymbol {\nabla }}$![]() , with a small multiple of $f_{\boldsymbol {\nabla } \boldsymbol {\nabla } }$
, with a small multiple of $f_{\boldsymbol {\nabla } \boldsymbol {\nabla } }$![]() added after an initial minimization of $f_{\boldsymbol {\nabla } }$
added after an initial minimization of $f_{\boldsymbol {\nabla } }$![]() .
.
The term $f_{\mathrm {well}}$![]() can be included to obtain configurations with a vacuum magnetic well, $d^2 V / d \psi ^2 < 0$
can be included to obtain configurations with a vacuum magnetic well, $d^2 V / d \psi ^2 < 0$![]() . Typically, $W_*$
. Typically, $W_*$![]() is set to a negative value to provide some margin against instability. Similarly, for configurations with pressure and/or current, $f_{\mathrm {Merc}}$
is set to a negative value to provide some margin against instability. Similarly, for configurations with pressure and/or current, $f_{\mathrm {Merc}}$![]() can be included to obtain Mercier-stable configurations. The value $D_*$
can be included to obtain Mercier-stable configurations. The value $D_*$![]() should be set to a positive value to provide a stability margin. It is unclear whether magnetic well and/or Mercier stability should be included in stellarator design, since multiple experiments have reported operating in unstable regimes without major difficulty (Geiger et al. Reference Geiger, Weller, Zarnstorff, Nührenberg, Werner and Kolesnichenko2004; Watanabe et al. Reference Watanabe, Sakakibara, Narushima, Funaba, Narihara, Tanaka, Yamaguchi, Toi, Ohdachi, Kaneko, Yamada, Suzuki, Cooper, Murakami, Nakajima, Yamada, Kawahata, Tokuzawa and Komori2005; Weller et al. Reference Weller, Sakakibara, Watanabe, Toi, Geiger, Zarnstorff, Hudson, Reiman, Werner, Nührenberg, Ohdachi, Suzuki and Yamada2006; de Aguilera et al. Reference de Aguilera, Castejon, Ascasibar, Blanco, de la Cal, Hidalgo, Liu, Lopez-Fraguas, Medina, Ochando, Pastor, Pedrosa, van Milligen and Velasco2015).
should be set to a positive value to provide a stability margin. It is unclear whether magnetic well and/or Mercier stability should be included in stellarator design, since multiple experiments have reported operating in unstable regimes without major difficulty (Geiger et al. Reference Geiger, Weller, Zarnstorff, Nührenberg, Werner and Kolesnichenko2004; Watanabe et al. Reference Watanabe, Sakakibara, Narushima, Funaba, Narihara, Tanaka, Yamaguchi, Toi, Ohdachi, Kaneko, Yamada, Suzuki, Cooper, Murakami, Nakajima, Yamada, Kawahata, Tokuzawa and Komori2005; Weller et al. Reference Weller, Sakakibara, Watanabe, Toi, Geiger, Zarnstorff, Hudson, Reiman, Werner, Nührenberg, Ohdachi, Suzuki and Yamada2006; de Aguilera et al. Reference de Aguilera, Castejon, Ascasibar, Blanco, de la Cal, Hidalgo, Liu, Lopez-Fraguas, Medina, Ochando, Pastor, Pedrosa, van Milligen and Velasco2015).
Whether an optimization produces a QA or QH configuration is determined by the initial condition for the axis shape. In a QH configuration with given $N$![]() , the axis normal vector rotates poloidally about the axis $N$
, the axis normal vector rotates poloidally about the axis $N$![]() times as one traverses the axis toroidally (as discussed in § 5.2 of Landreman & Sengupta Reference Landreman and Sengupta2018). QA configurations represent the $N=0$
times as one traverses the axis toroidally (as discussed in § 5.2 of Landreman & Sengupta Reference Landreman and Sengupta2018). QA configurations represent the $N=0$![]() case: the normal vector makes no net rotations about the axis as the axis is traversed toroidally. If the axis is continuously deformed from one $N$
case: the normal vector makes no net rotations about the axis as the axis is traversed toroidally. If the axis is continuously deformed from one $N$![]() value to another, the curvature crosses through zero, causing $f_{\boldsymbol {\nabla }}$
value to another, the curvature crosses through zero, causing $f_{\boldsymbol {\nabla }}$![]() , $f_{\boldsymbol {\nabla } \boldsymbol {\nabla } }$
, $f_{\boldsymbol {\nabla } \boldsymbol {\nabla } }$![]() and $f_{B2}$
and $f_{B2}$![]() to diverge. This results in an infinitely steep barrier in the objective function, which the optimizer will not cross. Hence the symmetry class ($N$
to diverge. This results in an infinitely steep barrier in the objective function, which the optimizer will not cross. Hence the symmetry class ($N$![]() value) of the optimum will match that of the initial condition.
value) of the optimum will match that of the initial condition.
The integrals (3.5)–(3.7) are discretized using a uniform grid in the standard toroidal angle $\phi$![]() with $N_\phi$
with $N_\phi$![]() points. Upon discretization, all the terms in $f$
points. Upon discretization, all the terms in $f$![]() have the form of a sum of squares. This is true also for the terms that are integrals over the axis, for instance,
have the form of a sum of squares. This is true also for the terms that are integrals over the axis, for instance,

Here, $j$![]() and $k$
and $k$![]() range over the $\boldsymbol{t}$
range over the $\boldsymbol{t}$![]() , $\boldsymbol{n}$
, $\boldsymbol{n}$![]() , $\boldsymbol{b}$
, $\boldsymbol{b}$![]() components, ${\rm \Delta} \phi$
components, ${\rm \Delta} \phi$![]() is the grid spacing in $\phi$
is the grid spacing in $\phi$![]() and the quantity in large square brackets is evaluated at the toroidal grid point $i$
and the quantity in large square brackets is evaluated at the toroidal grid point $i$![]() . The other terms in the objective involving integrals are discretized as
. The other terms in the objective involving integrals are discretized as

and

Therefore, the discretized problem can be solved using methods for nonlinear least-squares problems. The quantities in square brackets in (3.10)–(3.12) are the residuals for the least-squares problem.
It is effective to increase the dimensionality of the parameter space in several steps. For the first step, a maximum mode number $N_F=1$![]() is used, with $N_F$
is used, with $N_F$![]() incremented by one each step. For $N_F = 1,2,3$
incremented by one each step. For $N_F = 1,2,3$![]() , the weights $w_{\boldsymbol {\nabla } \boldsymbol {\nabla } }$
, the weights $w_{\boldsymbol {\nabla } \boldsymbol {\nabla } }$![]() , $w_{\mathrm {well}}$
, $w_{\mathrm {well}}$![]() and $w_{\mathrm {Merc}}$
and $w_{\mathrm {Merc}}$![]() are set to zero, which is found to make the optimization very robust. These weights are set to non-zero values if desired for later steps. As the number of Fourier modes in the parameter space is increased, the number of grid points $N_\phi$
are set to zero, which is found to make the optimization very robust. These weights are set to non-zero values if desired for later steps. As the number of Fourier modes in the parameter space is increased, the number of grid points $N_\phi$![]() can be increased as well (as is done for results here).
can be increased as well (as is done for results here).
We solve the optimization problem using the C++ implementation at https://github.com/landreman/qsc, also archived at Landreman (Reference Landreman2022). Results here are obtained with the Levenberg–Marquardt algorithm implemented in the GNU scientific library (Galassi et al. Reference Galassi2009).
4. Parameter scans
Parameter scans are applied to the optimization problem of § 3, to understand the set of possible quasisymmetric configurations. The parameters scanned include $n_{\mathrm {fp}}$![]() , the $w_j$
, the $w_j$![]() weights in (3.2), the target values $\iota _*$
weights in (3.2), the target values $\iota _*$![]() , $L_*$
, $L_*$![]() , $W_*$
, $W_*$![]() and $D_*$
and $D_*$![]() , the pressure $p_2$
, the pressure $p_2$![]() , whether or not magnetic well or Mercier stability is imposed, and whether QA or QH is sought. The number of field periods is scanned from one through 10. In each case, the initial axis shape before optimization is $R(\phi )=1+\varDelta \cos (n_{\mathrm {fp}} \phi )$
, whether or not magnetic well or Mercier stability is imposed, and whether QA or QH is sought. The number of field periods is scanned from one through 10. In each case, the initial axis shape before optimization is $R(\phi )=1+\varDelta \cos (n_{\mathrm {fp}} \phi )$![]() and $Z(\phi )=\varDelta \sin (n_{\mathrm {fp}} \phi )$
and $Z(\phi )=\varDelta \sin (n_{\mathrm {fp}} \phi )$![]() for a chosen number $\varDelta$
for a chosen number $\varDelta$![]() . When searching for QA solutions, $\varDelta$
. When searching for QA solutions, $\varDelta$![]() is chosen $<1/(n_{\mathrm {fp}}^2+1)$
is chosen $<1/(n_{\mathrm {fp}}^2+1)$![]() so the normal vector does not make complete poloidal rotations, $w_L$
so the normal vector does not make complete poloidal rotations, $w_L$![]() is set to 0 and $\iota _*$
is set to 0 and $\iota _*$![]() is scanned. When searching for QH solutions, $\varDelta$
is scanned. When searching for QH solutions, $\varDelta$![]() is chosen $>1/(n_{\mathrm {fp}}^2+1)$
is chosen $>1/(n_{\mathrm {fp}}^2+1)$![]() so the normal vector makes $n_{\mathrm {fp}}$
so the normal vector makes $n_{\mathrm {fp}}$![]() complete poloidal rotations, $w_\iota$
complete poloidal rotations, $w_\iota$![]() is set to 0 and $L_*$
is set to 0 and $L_*$![]() is scanned. These conditions on $\varDelta$
is scanned. These conditions on $\varDelta$![]() have been discussed recently by Rodriguez, Sengupta & Bhattacharjee (Reference Rodriguez, Sengupta and Bhattacharjee2022a). The weight $w_{\boldsymbol {\nabla }}$
have been discussed recently by Rodriguez, Sengupta & Bhattacharjee (Reference Rodriguez, Sengupta and Bhattacharjee2022a). The weight $w_{\boldsymbol {\nabla }}$![]() is always 1, since $f_{\boldsymbol {\nabla }}$
is always 1, since $f_{\boldsymbol {\nabla }}$![]() is the most reliable term to include in the objective, as discussed in the previous section. The other weights are scanned logarithmically over several orders of magnitude.
is the most reliable term to include in the objective, as discussed in the previous section. The other weights are scanned logarithmically over several orders of magnitude.
For many choices of weights and targets, the configuration at the end of an optimization may be unacceptable if the volume of good quasisymmetry is too small, the rotational transform is too low, the elongation is too large, etc. Therefore, as the parameters are scanned, configurations are saved only if they pass through several filters, i.e. satisfy several inequalities. One such filter is $|\iota | > 0.2$![]() ; sufficient $\iota$
; sufficient $\iota$![]() is required since the equilibrium $\beta$
is required since the equilibrium $\beta$![]() limit scales $\propto \iota ^2$
limit scales $\propto \iota ^2$![]() , and the width of banana orbits in QA scales $\propto 1 / \iota$
, and the width of banana orbits in QA scales $\propto 1 / \iota$![]() . Other typical inequalities imposed are $L_{\boldsymbol {\nabla } B} > 0.2 R_0$
. Other typical inequalities imposed are $L_{\boldsymbol {\nabla } B} > 0.2 R_0$![]() , $L_{\boldsymbol {\nabla } \boldsymbol {\nabla } B} > 0.2 R_0$
, $L_{\boldsymbol {\nabla } \boldsymbol {\nabla } B} > 0.2 R_0$![]() , the variation of $B_{20}$
, the variation of $B_{20}$![]() is $< B_0$
is $< B_0$![]() , elongation in the plane perpendicular to the axis $< 10$
, elongation in the plane perpendicular to the axis $< 10$![]() (computed from the $O(r^1)$
(computed from the $O(r^1)$![]() elliptical surfaces) and minimum minor radius $r_c > 0.15 R_0$
elliptical surfaces) and minimum minor radius $r_c > 0.15 R_0$![]() . A minimum $R(\phi )/R_0$
. A minimum $R(\phi )/R_0$![]() is enforced, e.g. $> 0.4$
is enforced, e.g. $> 0.4$![]() , to ensure some space for coils near the coordinate origin. The quantities $|X_{20}|$
, to ensure some space for coils near the coordinate origin. The quantities $|X_{20}|$![]() , $|X_{2s}|$
, $|X_{2s}|$![]() , $|X_{2c}|$
, $|X_{2c}|$![]() , $|Y_{20}|$
, $|Y_{20}|$![]() , $|Y_{2s}|$
, $|Y_{2s}|$![]() , $|Y_{2c}|$
, $|Y_{2c}|$![]() , $|Z_{20}|$
, $|Z_{20}|$![]() , $|Z_{2s}|$
, $|Z_{2s}|$![]() and $|Z_{2c}|$
and $|Z_{2c}|$![]() are required to be below a threshold such as 10.0. This constraint is another heuristic method for ensuring the radius of applicability of the asymptotic series is relatively large, by ensuring the $O(r^2)$
are required to be below a threshold such as 10.0. This constraint is another heuristic method for ensuring the radius of applicability of the asymptotic series is relatively large, by ensuring the $O(r^2)$![]() terms are not too much larger than the $O(r^1)$
terms are not too much larger than the $O(r^1)$![]() terms. Similarly, the quantities $|\partial X_{20} / \partial \varphi |$
terms. Similarly, the quantities $|\partial X_{20} / \partial \varphi |$![]() , $|\partial X_{2s} / \partial \varphi |$
, $|\partial X_{2s} / \partial \varphi |$![]() , $|\partial X_{2c} / \partial \varphi |$
, $|\partial X_{2c} / \partial \varphi |$![]() , $|\partial Y_{20} / \partial \varphi |$
, $|\partial Y_{20} / \partial \varphi |$![]() , $|\partial Y_{2s} / \partial \varphi |$
, $|\partial Y_{2s} / \partial \varphi |$![]() , $|\partial Y_{2c} / \partial \varphi |$
, $|\partial Y_{2c} / \partial \varphi |$![]() , $|\partial Z_{20} / \partial \varphi |$
, $|\partial Z_{20} / \partial \varphi |$![]() , $|\partial Z_{2s} / \partial \varphi |$
, $|\partial Z_{2s} / \partial \varphi |$![]() and $|\partial Z_{2c} / \partial \varphi |$
and $|\partial Z_{2c} / \partial \varphi |$![]() are required to be below a threshold such as 20.0. The exact values of the thresholds are adjusted from case to case; for instance it is harder to find high-$\beta$
are required to be below a threshold such as 20.0. The exact values of the thresholds are adjusted from case to case; for instance it is harder to find high-$\beta$![]() configurations with Mercier stability so generous thresholds are used in this case. In contrast, vacuum configurations without a magnetic well constraint are comparatively easier to obtain, so more restrictive thresholds are used in this case to focus on the most interesting solutions.
configurations with Mercier stability so generous thresholds are used in this case. In contrast, vacuum configurations without a magnetic well constraint are comparatively easier to obtain, so more restrictive thresholds are used in this case to focus on the most interesting solutions.
The results of the parameter scans are shown in figure 3. Each point indicates an independent optimization for specific choices of weights and target values. The points are coloured to indicate $n_{\mathrm {fp}}$![]() and QA vs QH symmetry. The horizontal coordinate is the length of the magnetic axis, normalized so that 1 indicates a circle, while larger values indicate greater helical excursion of the axis. The axes of the figure were taken to be axis length vs $\iota$
and QA vs QH symmetry. The horizontal coordinate is the length of the magnetic axis, normalized so that 1 indicates a circle, while larger values indicate greater helical excursion of the axis. The axes of the figure were taken to be axis length vs $\iota$![]() since this choice effectively separates the data into clusters. The apparent stripes at fixed axis length are an artefact of the grid of target $L_*$
since this choice effectively separates the data into clusters. The apparent stripes at fixed axis length are an artefact of the grid of target $L_*$![]() values in the scans. The database of configurations includes both vacuum and finite-$\beta$
values in the scans. The database of configurations includes both vacuum and finite-$\beta$![]() cases (i.e. various choices of $p_2$
cases (i.e. various choices of $p_2$![]() ), with and without magnetic well, and with and without Mercier stability.
), with and without magnetic well, and with and without Mercier stability.

Figure 3. Results from optimizing the near-axis parameters, scanning the weights, targets and $n_{\mathrm {fp}}$![]() . Each point indicates the result of an optimization. Five representative points are highlighted with visualizations of the flux surfaces in three dimensions and are discussed in § 5.
. Each point indicates the result of an optimization. Five representative points are highlighted with visualizations of the flux surfaces in three dimensions and are discussed in § 5.
A total of $5\times 10^5$![]() points are plotted in figure 3. As discussed above, most optimizations resulted in configurations that were filtered out, so a total of $> 10^7$
points are plotted in figure 3. As discussed above, most optimizations resulted in configurations that were filtered out, so a total of $> 10^7$![]() optimizations were run to produce the figure. Each optimization involved many evaluations of the objective function, (3.2), so a total of $> 10^{11}$
optimizations were run to produce the figure. Each optimization involved many evaluations of the objective function, (3.2), so a total of $> 10^{11}$![]() evaluations of the objective were performed to produce the figure. Each function evaluation typically takes under 1 ms. The speed by which the near-axis equations can be evaluated makes it possible to evaluate this very large number of configurations in tens of wallclock hours on a computing cluster.
evaluations of the objective were performed to produce the figure. Each function evaluation typically takes under 1 ms. The speed by which the near-axis equations can be evaluated makes it possible to evaluate this very large number of configurations in tens of wallclock hours on a computing cluster.
Many interesting patterns can be seen in the data. The QA solutions are limited to a single continuous band for each $n_{\mathrm {fp}}$![]() at the lower left, with $\iota < 1$
at the lower left, with $\iota < 1$![]() and relatively circular magnetic axis. The QH solutions are found at a wide range of $\iota$
and relatively circular magnetic axis. The QH solutions are found at a wide range of $\iota$![]() , from just below 1 up to ${>}4$
, from just below 1 up to ${>}4$![]() . The QH solutions for any given $n_{\mathrm {fp}}$
. The QH solutions for any given $n_{\mathrm {fp}}$![]() also occupy continuous bands with a wide range of axis lengths. Analogous features have been observed recently by Rodriguez et al. (Reference Rodriguez, Sengupta and Bhattacharjee2022b).
also occupy continuous bands with a wide range of axis lengths. Analogous features have been observed recently by Rodriguez et al. (Reference Rodriguez, Sengupta and Bhattacharjee2022b).
As with QH symmetry, QA symmetry scans were performed for all values of $n_{\mathrm {fp}}$![]() from 1 through 10. However, no configurations passed the filters for $n_{\mathrm {fp}} > 3$
from 1 through 10. However, no configurations passed the filters for $n_{\mathrm {fp}} > 3$![]() . (For example, for QA with $n_{\mathrm {fp}}=4$
. (For example, for QA with $n_{\mathrm {fp}}=4$![]() and no constraints other than $\iota >0.2$
and no constraints other than $\iota >0.2$![]() , the largest $r_c$
, the largest $r_c$![]() obtained was only $0.11 R_0$
obtained was only $0.11 R_0$![]() .) These findings are consistent with previous reports of QA only for $n_{\mathrm {fp}}=2$
.) These findings are consistent with previous reports of QA only for $n_{\mathrm {fp}}=2$![]() and 3. Furthermore, in the scans here, the QA configurations for $n_{\mathrm {fp}}=3$
and 3. Furthermore, in the scans here, the QA configurations for $n_{\mathrm {fp}}=3$![]() had smaller values of $r_c$
had smaller values of $r_c$![]() than the $n_{\mathrm {fp}}=2$
than the $n_{\mathrm {fp}}=2$![]() QAs: specifically $r_c$
QAs: specifically $r_c$![]() was $<0.2$
was $<0.2$![]() for $n_{\mathrm {fp}}=3$
for $n_{\mathrm {fp}}=3$![]() , whereas $r_c$
, whereas $r_c$![]() attained values up to 1.0 for $n_{\mathrm {fp}}=2$
attained values up to 1.0 for $n_{\mathrm {fp}}=2$![]() . Therefore, in the $n_{\mathrm {fp}}=3$
. Therefore, in the $n_{\mathrm {fp}}=3$![]() configurations, the region of good quasisymmetry is limited to a higher aspect ratio. This finding is consistent with the fact that previous optimizations for QA at $n_{\mathrm {fp}}=3$
configurations, the region of good quasisymmetry is limited to a higher aspect ratio. This finding is consistent with the fact that previous optimizations for QA at $n_{\mathrm {fp}}=3$![]() (NCSX and ARIES-CS) have had significant imperfections in the symmetry, whereas excellent QA has been obtained at $n_{\mathrm {fp}}=2$
(NCSX and ARIES-CS) have had significant imperfections in the symmetry, whereas excellent QA has been obtained at $n_{\mathrm {fp}}=2$![]() (Giuliani et al. Reference Giuliani, Wechsung, Landreman, Stadler and Cerfon2022; Landreman & Paul Reference Landreman and Paul2022). When $n_{\mathrm {fp}}=1$
(Giuliani et al. Reference Giuliani, Wechsung, Landreman, Stadler and Cerfon2022; Landreman & Paul Reference Landreman and Paul2022). When $n_{\mathrm {fp}}=1$![]() , QA solutions were found that satisfied all constraints, but they resembled $n_{\mathrm {fp}}=2$
, QA solutions were found that satisfied all constraints, but they resembled $n_{\mathrm {fp}}=2$![]() configurations that were translated or rotated to break two-field-period symmetry. These configurations did not appear to have an advantage over $n_{\mathrm {fp}}=2$
configurations that were translated or rotated to break two-field-period symmetry. These configurations did not appear to have an advantage over $n_{\mathrm {fp}}=2$![]() configurations and so will not be considered further.
configurations and so will not be considered further.
In contrast, QH solutions were found that passed the filters for all values of $n_{\mathrm {fp}}$![]() attempted except 1. For QH solutions, the number of field periods for which the axis length can be minimized is 4, followed closely by 3 and 5. For other values of $n_{\mathrm {fp}}$
attempted except 1. For QH solutions, the number of field periods for which the axis length can be minimized is 4, followed closely by 3 and 5. For other values of $n_{\mathrm {fp}}$![]() , QH solutions require significant helical excursion of the axis and an associated longer axis length.
, QH solutions require significant helical excursion of the axis and an associated longer axis length.
A related but different parameter scan was shown previously in figure 2 of Boozer (Reference Boozer2020). That previous scan used only the $O(r)$![]() terms in the expansion rather than $O(r^2)$
terms in the expansion rather than $O(r^2)$![]() , and the Fourier modes of the axis were scanned directly, with no optimization applied. The filters used in the present figure 3 eliminate significant parts of the parameter space from the earlier scan. This can be seen for example in the more limited ranges of $\iota$
, and the Fourier modes of the axis were scanned directly, with no optimization applied. The filters used in the present figure 3 eliminate significant parts of the parameter space from the earlier scan. This can be seen for example in the more limited ranges of $\iota$![]() for each value of $N$
for each value of $N$![]() in the present figure 3 compared with the previous scan.
in the present figure 3 compared with the previous scan.
For five of the points in figure 3, the flux surface shapes of the associated optimized configurations are shown in the same figure in three dimensions. These configurations and others from the scan are discussed in greater detail in § 5. Of these highlighted configurations, the two on the left are relatively familiar in shape: a two-field-period QA resembling CFQS (the Chinese First Quasi-axisymmetric Stellarator, Liu et al. Reference Liu, Shimizu, Isobe, Okamura, Nishimura, Suzuki, Xu, Zhang, Liu and Huang2018), and a four-field-period QH resembling HSX (the Helically Symmetric eXperiment, Anderson et al. Reference Anderson, Almagri, Anderson, Matthews, Talmadge and Shohet1995). One of the other highlighted configurations is a four-field-period QH with large helical excursion of the axis, more excursion than in previously described QH stellarators aside from the recent configuration by Rodriguez et al. (Reference Rodriguez, Sengupta and Bhattacharjee2022b). The other two configurations shown in three dimensions have shapes unlike previously reported quasisymmetric stellarators. These include QH configurations with unusual numbers of field periods, two and seven.
5. Example configurations
We now present several specific configurations obtained using the parameter scans in § 4. All input and output files for these configurations and the optimizations that led to them can be found in the supplemental material on Zenodo (Landreman Reference Landreman2022).
For each configuration, a finite aspect ratio is chosen for the figures. The finite-aspect-ratio boundary is generated as described in § 4.2 of Landreman et al. (Reference Landreman, Sengupta and Plunk2019). Namely, a finite value $a$![]() is chosen for the minor radius variable $r$
is chosen for the minor radius variable $r$![]() , the position vector (2.2) is evaluated for $r=a$
, the position vector (2.2) is evaluated for $r=a$![]() and the result is converted to Fourier series in cylindrical coordinates. To evaluate the position vector, some $O(r^3)$
and the result is converted to Fourier series in cylindrical coordinates. To evaluate the position vector, some $O(r^3)$![]() terms are included, as detailed in § 3 of Landreman & Sengupta (Reference Landreman and Sengupta2019). For each boundary surface, several definitions of the aspect ratio are available. In the near-axis equations, a convenient definition of aspect ratio is $R_0/a$
terms are included, as detailed in § 3 of Landreman & Sengupta (Reference Landreman and Sengupta2019). For each boundary surface, several definitions of the aspect ratio are available. In the near-axis equations, a convenient definition of aspect ratio is $R_0/a$![]() . However, this definition differs from the widely used definition of aspect ratio in the stellarator community, $A=\bar {R}/\bar {a}$
. However, this definition differs from the widely used definition of aspect ratio in the stellarator community, $A=\bar {R}/\bar {a}$![]() , which is obtained as follows. The effective minor radius $\bar {a}$
, which is obtained as follows. The effective minor radius $\bar {a}$![]() is defined by setting the toroidally averaged cross-sectional area of the shaped boundary equal to the area of a circle with minor radius $\bar {a}$
is defined by setting the toroidally averaged cross-sectional area of the shaped boundary equal to the area of a circle with minor radius $\bar {a}$![]() . Then the effective major radius $\bar {R}$
. Then the effective major radius $\bar {R}$![]() is defined by setting the volume of the shaped boundary equal to that of a circular cross-section axisymmetric torus with major radius $\bar {R}$
is defined by setting the volume of the shaped boundary equal to that of a circular cross-section axisymmetric torus with major radius $\bar {R}$![]() . (See p. 12 of Landreman & Sengupta (Reference Landreman and Sengupta2019) for details.)
. (See p. 12 of Landreman & Sengupta (Reference Landreman and Sengupta2019) for details.)
To confirm the correctness of the near-axis method, each example below is checked using a fixed-boundary MHD equilibrium calculation that does not make a near-axis expansion, as follows. Given the constructed boundary, the field inside is computed and converted to Boozer coordinates with the DESC code (Dudt & Kolemen Reference Dudt and Kolemen2020; Conlin et al. Reference Conlin, Dudt, Panici and Kolemen2022; Dudt et al. Reference Dudt, Conlin, Panici and Kolemen2022; Panici et al. Reference Panici, Conlin, Dudt and Kolemen2022). Similar checks of near-axis solutions were done using the VMEC code (Hirshman & Whitson Reference Hirshman and Whitson1983) previously in Landreman et al. (Reference Landreman, Sengupta and Plunk2019), Plunk et al. (Reference Plunk, Landreman and Helander2019), Landreman & Sengupta (Reference Landreman and Sengupta2019) and Landreman & Jorge (Reference Landreman and Jorge2020). It was shown in this previous work that $\iota$![]() , $d^2V/d\psi ^2$
, $d^2V/d\psi ^2$![]() , $D_{\mathrm {Merc}}$
, $D_{\mathrm {Merc}}$![]() and Fourier modes of $B$
and Fourier modes of $B$![]() for fully 3-D equilibria converged to the values predicted by the near-axis solution as the aspect ratio increased. No further optimization is applied to the finite-aspect-ratio configurations here, although this could be done in future work.
for fully 3-D equilibria converged to the values predicted by the near-axis solution as the aspect ratio increased. No further optimization is applied to the finite-aspect-ratio configurations here, although this could be done in future work.
For the examples that follow, the finite minor radius $a$![]() is chosen by hand based on several considerations. The spectral width of the constructed boundary should be sufficiently small that the DESC calculations reach acceptable force residuals with poloidal and toroidal mode numbers $\le 12$
is chosen by hand based on several considerations. The spectral width of the constructed boundary should be sufficiently small that the DESC calculations reach acceptable force residuals with poloidal and toroidal mode numbers $\le 12$![]() . This is easier to achieve for smaller $a$
. This is easier to achieve for smaller $a$![]() . Also $a$
. Also $a$![]() is chosen to be sufficiently small that $B$
is chosen to be sufficiently small that $B$![]() from the DESC solution is reasonably similar to the near-axis prediction.
from the DESC solution is reasonably similar to the near-axis prediction.
5.1. Quasi-axisymmetry with two periods
The first configuration is one that is very similar to the QA with magnetic well presented in Landreman & Paul (Reference Landreman and Paul2022). That configuration was a two-field-period vacuum field optimized for $\iota \sim 0.42$![]() , and so in the near-axis calculation we set $p_2=0$
, and so in the near-axis calculation we set $p_2=0$![]() and $\iota _*=0.42$
and $\iota _*=0.42$![]() . Other than these values, the near-axis optimization is completely independent of the configuration and optimization in Landreman & Paul (Reference Landreman and Paul2022). For the first three steps of the near-axis optimization, in which the number of Fourier modes is increased from $N_F=1$
. Other than these values, the near-axis optimization is completely independent of the configuration and optimization in Landreman & Paul (Reference Landreman and Paul2022). For the first three steps of the near-axis optimization, in which the number of Fourier modes is increased from $N_F=1$![]() to $N_F=3$
to $N_F=3$![]() , the only non-zero weights are $w_{\boldsymbol {\nabla }}=1$
, the only non-zero weights are $w_{\boldsymbol {\nabla }}=1$![]() , $w_\iota =100$
, $w_\iota =100$![]() and $w_{B2}=0.01$
and $w_{B2}=0.01$![]() . Then, in steps with $N_F=3- 7$
. Then, in steps with $N_F=3- 7$![]() , the weights used are $w_{\boldsymbol {\nabla }}=w_{\boldsymbol {\nabla } \boldsymbol {\nabla } }=w_{\mathrm {well}}=1$
, the weights used are $w_{\boldsymbol {\nabla }}=w_{\boldsymbol {\nabla } \boldsymbol {\nabla } }=w_{\mathrm {well}}=1$![]() , $w_{\iota }=100$
, $w_{\iota }=100$![]() and $w_{B2}=30$
and $w_{B2}=30$![]() . A target magnetic well of $W_*=-20$
. A target magnetic well of $W_*=-20$![]() is used to provide some margin. (The DESC calculations at finite aspect ratio had less magnetic well than the near-axis solution, so $W_*=-20$
is used to provide some margin. (The DESC calculations at finite aspect ratio had less magnetic well than the near-axis solution, so $W_*=-20$![]() was found to be sufficient to achieve a magnetic well at all radii in the DESC solution.) For later configurations in this paper, the optimization weights and target values can be found in Landreman (Reference Landreman2022). The full multi-stage optimization takes a total of 0.4 seconds on 1 cpu of a standard MacBook laptop. The flux surface shape at aspect ratio $A=6$
was found to be sufficient to achieve a magnetic well at all radii in the DESC solution.) For later configurations in this paper, the optimization weights and target values can be found in Landreman (Reference Landreman2022). The full multi-stage optimization takes a total of 0.4 seconds on 1 cpu of a standard MacBook laptop. The flux surface shape at aspect ratio $A=6$![]() is displayed in figure 4, matching the aspect ratio used in Landreman & Paul (Reference Landreman and Paul2022). Cross-sections and 3-D renderings of the same two configurations, scaled to the same average major radius, are also shown in figure 4. It can be seen that the surface shape generated by the near-axis method is qualitatively similar to the one obtained independently by finite-aspect-ratio optimization. The field strength computed by DESC on the aspect ratio 6 boundary is displayed as a function of the Boozer angles in figure 5. It can be seen that QA is achieved approximately, although not as accurately as it is with finite-aspect-ratio optimization. The figure also shows a similar calculation for the boundary constructed at a higher aspect ratio, 10, showing that the symmetry improves at higher aspect ratio, as expected. Indeed, as the aspect ratio is increased, QA can be achieved to any desired precision, as demonstrated in Landreman & Sengupta (Reference Landreman and Sengupta2019). Overall, we can conclude that while the near-axis approach is not as accurate as finite-aspect-ratio optimization, it can compute qualitatively similar configurations extremely fast.
is displayed in figure 4, matching the aspect ratio used in Landreman & Paul (Reference Landreman and Paul2022). Cross-sections and 3-D renderings of the same two configurations, scaled to the same average major radius, are also shown in figure 4. It can be seen that the surface shape generated by the near-axis method is qualitatively similar to the one obtained independently by finite-aspect-ratio optimization. The field strength computed by DESC on the aspect ratio 6 boundary is displayed as a function of the Boozer angles in figure 5. It can be seen that QA is achieved approximately, although not as accurately as it is with finite-aspect-ratio optimization. The figure also shows a similar calculation for the boundary constructed at a higher aspect ratio, 10, showing that the symmetry improves at higher aspect ratio, as expected. Indeed, as the aspect ratio is increased, QA can be achieved to any desired precision, as demonstrated in Landreman & Sengupta (Reference Landreman and Sengupta2019). Overall, we can conclude that while the near-axis approach is not as accurate as finite-aspect-ratio optimization, it can compute qualitatively similar configurations extremely fast.

Figure 4. Optimization of near-axis solutions and traditional finite-aspect-ratio optimization, run completely independently, can yield similar results. Here, both methods are used to generate a two-field-period vacuum QA with $\iota \approx 0.42$![]() and magnetic well at aspect ratio 6.0. (a) Cross-sections of the results are plotted at three toroidal angles, showing the similar surface shapes. (b) Views of the same configurations in three dimensions. The finite-aspect-ratio optimization is from Landreman & Paul (Reference Landreman and Paul2022).
and magnetic well at aspect ratio 6.0. (a) Cross-sections of the results are plotted at three toroidal angles, showing the similar surface shapes. (b) Views of the same configurations in three dimensions. The finite-aspect-ratio optimization is from Landreman & Paul (Reference Landreman and Paul2022).

Figure 5. By computing the field inside the boundary constructed from the near-axis solution, it can be confirmed that approximate QA symmetry was indeed achieved. The symmetry errors decrease as the aspect ratio increases, as expected. For comparison, the finite-aspect-ratio ‘QA+well’ optimization from Landreman & Paul (Reference Landreman and Paul2022) is shown at right.
5.2. Quasi-helical symmetry with two periods
One noteworthy discovery from the parameter scan is that there are QH solutions with only two field periods. To our knowledge, two-field-period QH configurations have not been reported previously. These configurations may be attractive since the number of modular coils tends to scale with the number of field periods. Therefore a two-field-period QH may require fewer coils than other QH configurations, reducing cost and enabling greater access between coils. At the same time, QH configurations can have very good confinement of energetic particles (Bader et al. Reference Bader, Anderson, Drevlak, Faber, Hegna, Henneberg, Landreman, Schmitt, Suzuki and Ware2021; Landreman & Paul Reference Landreman and Paul2022; Paul et al. Reference Paul, Bhattacharjee, Landreman, Alex, Velasco and Nies2022) due to the thinner banana orbits and related factors.
A two-field-period QH configuration generated by the optimization procedure here is shown in figure 6. This configuration is a vacuum field with $\iota =0.95$![]() , and the surface plotted has $a / R_{0} = 0.12$
, and the surface plotted has $a / R_{0} = 0.12$![]() . When viewed from one side, the configuration resembles the original figure-eight design proposed by Spitzer (Reference Spitzer1958). However, in contrast to Spitzer's design, the new configuration here has a non-circular cross-section yielding QH symmetry, providing improved confinement. A challenge for this new configuration is that there is not much space in the middle for coils. An important question for future research is whether $n_{\mathrm {fp}}=2$
. When viewed from one side, the configuration resembles the original figure-eight design proposed by Spitzer (Reference Spitzer1958). However, in contrast to Spitzer's design, the new configuration here has a non-circular cross-section yielding QH symmetry, providing improved confinement. A challenge for this new configuration is that there is not much space in the middle for coils. An important question for future research is whether $n_{\mathrm {fp}}=2$![]() QH configurations can be found with more space in the middle, and whether feasible coil solutions exist.
QH configurations can be found with more space in the middle, and whether feasible coil solutions exist.

Figure 6. A two-field-period quasi-helically symmetric stellarator generated from the near-axis method. (a) Cross-sections. (b) The same configuration is shown from three perspectives. Colour indicates the field strength, and black curves are field lines.
It takes many toroidal Fourier modes to represent this configuration in cylindrical coordinates due to the strong shaping, with regions at small major radius and with high inclination with respect to the $z=0$![]() plane. It may be for this reason that $n_{\mathrm {fp}}=2$
plane. It may be for this reason that $n_{\mathrm {fp}}=2$![]() QH configurations have not been reported previously. Here, for the near-axis calculations, 11 Fourier modes are used to represent $R(\phi )$
QH configurations have not been reported previously. Here, for the near-axis calculations, 11 Fourier modes are used to represent $R(\phi )$![]() and $Z(\phi )$
and $Z(\phi )$![]() .
.
Figure 7 shows a fully 3-D calculation of $B$![]() for this configuration with $a/R_0=0.05$
for this configuration with $a/R_0=0.05$![]() . It can be seen that the $B$
. It can be seen that the $B$![]() contours are (mostly) straight and diagonal, confirming the desired QH symmetry.
contours are (mostly) straight and diagonal, confirming the desired QH symmetry.

Figure 7. Magnetic field strength on the $a/R_0=0.05$![]() surface of the two-field-period quasi-helically symmetric stellarator, computed by running a fully 3-D fixed-boundary equilibrium calculation inside the boundary constructed from the near-axis method. The mostly straight diagonal contours confirm the QH symmetry.
surface of the two-field-period quasi-helically symmetric stellarator, computed by running a fully 3-D fixed-boundary equilibrium calculation inside the boundary constructed from the near-axis method. The mostly straight diagonal contours confirm the QH symmetry.
5.3. Quasi-helical symmetry with three field periods
Next, we consider QH configurations in which the number of field periods is three. Previously, a configuration with these properties, obtained using conventional finite-aspect-ratio optimization, was reported in Ku & Boozer (Reference Ku and Boozer2011). Here, we show two new such configurations obtained with the near-axis method.
First, figure 8 shows a vacuum configuration. The only terms included in the optimization were $f_L$![]() , $f_{\boldsymbol {\nabla }}$
, $f_{\boldsymbol {\nabla }}$![]() , $f_{\boldsymbol {\nabla } \boldsymbol {\nabla } }$
, $f_{\boldsymbol {\nabla } \boldsymbol {\nabla } }$![]() , $f_{B2}$
, $f_{B2}$![]() . The rotational transform obtained is $\iota = 1.25$
. The rotational transform obtained is $\iota = 1.25$![]() . For the 3-D views and cross-sections in figure 8, a minor radius of $a = 0.15\ R_0$
. For the 3-D views and cross-sections in figure 8, a minor radius of $a = 0.15\ R_0$![]() is used, corresponding to an aspect ratio $A=5$
is used, corresponding to an aspect ratio $A=5$![]() . The field strength in Boozer coordinates on this boundary computed with DESC is shown in the left panel of figure 9, confirming the expected QH symmetry.
. The field strength in Boozer coordinates on this boundary computed with DESC is shown in the left panel of figure 9, confirming the expected QH symmetry.

Figure 8. A three-field-period quasi-helically symmetric stellarator generated from the near-axis method, for $\beta =0$![]() . (a) Cross-sections. (b) The same configuration is shown from three perspectives. Colour indicates the field strength, and black curves are field lines.
. (a) Cross-sections. (b) The same configuration is shown from three perspectives. Colour indicates the field strength, and black curves are field lines.

Figure 9. Magnetic field strength on the surface of the three-field-period quasi-helically symmetric stellarators, computed by running fully 3-D fixed-boundary equilibrium calculations inside the boundaries constructed from the near-axis method.
Second, a finite-$\beta$![]() configuration is shown in figure 10. The pressure is introduced by setting $p_2$
configuration is shown in figure 10. The pressure is introduced by setting $p_2$![]() equal to a non-zero value, in this case $-2.0\times 10^{6}$
equal to a non-zero value, in this case $-2.0\times 10^{6}$![]() Pa m$^{-2}$
Pa m$^{-2}$![]() , with the negative sign corresponding to a typical peaked profile. Note that, for a given objective function, optimizations run at non-zero $p_2$
, with the negative sign corresponding to a typical peaked profile. Note that, for a given objective function, optimizations run at non-zero $p_2$![]() generally result in different axis shapes and flux surface shapes compared with optimizations with $p_2=0$
generally result in different axis shapes and flux surface shapes compared with optimizations with $p_2=0$![]() . The rotational transform for the configuration here is $\iota = 1.09$
. The rotational transform for the configuration here is $\iota = 1.09$![]() . Note also that the absolute pressure associated with any fixed $p_2$
. Note also that the absolute pressure associated with any fixed $p_2$![]() depends on the aspect ratio. For a pressure profile $p(r)=p_0 + r^2 p_2$
depends on the aspect ratio. For a pressure profile $p(r)=p_0 + r^2 p_2$![]() with $p=0$
with $p=0$![]() at a boundary $r=a$
at a boundary $r=a$![]() , the volume-averaged $\beta$
, the volume-averaged $\beta$![]() is $\langle \beta \rangle =2\mu _0 \langle {p}\rangle / B_0^2$
is $\langle \beta \rangle =2\mu _0 \langle {p}\rangle / B_0^2$![]() , where $\langle {p}\rangle =(2/a^2)\int _0^a pr\, dr=p_0/2$
, where $\langle {p}\rangle =(2/a^2)\int _0^a pr\, dr=p_0/2$![]() is a volume-averaged pressure, giving $\langle \beta \rangle =-\mu _0 p_2 a^2 / B_0^2$
is a volume-averaged pressure, giving $\langle \beta \rangle =-\mu _0 p_2 a^2 / B_0^2$![]() . Hence, for a given $p_2$
. Hence, for a given $p_2$![]() , a larger minor radius corresponds to a larger averaged $\beta$
, a larger minor radius corresponds to a larger averaged $\beta$![]() . For the figures we choose a boundary minor radius $a/R_0=0.13$
. For the figures we choose a boundary minor radius $a/R_0=0.13$![]() , slightly smaller than for the vacuum case since the QH symmetry is somewhat worse with finite pressure. At this minor radius, the aspect ratio is $A=6.5$
, slightly smaller than for the vacuum case since the QH symmetry is somewhat worse with finite pressure. At this minor radius, the aspect ratio is $A=6.5$![]() and $\langle \beta \rangle = 4\,\%$
and $\langle \beta \rangle = 4\,\%$![]() . The field strength in Boozer coordinates on this boundary from a finite-aspect-ratio equilibrium calculation is shown in the right panel of figure 9, confirming the expected QH symmetry. As discussed previously, a toroidal current profile $I(\psi )=0$
. The field strength in Boozer coordinates on this boundary from a finite-aspect-ratio equilibrium calculation is shown in the right panel of figure 9, confirming the expected QH symmetry. As discussed previously, a toroidal current profile $I(\psi )=0$![]() is used for this finite-aspect-ratio equilibrium calculation.
is used for this finite-aspect-ratio equilibrium calculation.

Figure 10. A three-field-period quasi-helically symmetric stellarator generated from the near-axis method, for $\langle \beta \rangle =4\,\%$![]() . (a) Cross-sections. (b) The same configuration is shown from three perspectives. Colour indicates the field strength, and black curves are field lines.
. (a) Cross-sections. (b) The same configuration is shown from three perspectives. Colour indicates the field strength, and black curves are field lines.
5.4. Quasi-helical symmetry with four field periods
Next, we consider QH configurations with four field periods. This number of field periods has been a common choice in previous QH designs (Anderson et al. Reference Anderson, Almagri, Anderson, Matthews, Talmadge and Shohet1995; Ku & Boozer Reference Ku and Boozer2011; Bader et al. Reference Bader, Faber, Schmitt, Anderson, Drevlak, Duff, Frerichs, Hegna, Kruger and Landreman2020; Landreman & Paul Reference Landreman and Paul2022). We will show three configurations in this category.
The first is a configuration with relatively long magnetic axis, $L / R_0 = 12$![]() . This configuration is relatively far to the right on the band of four-field-period QH data in figure 3. It is a vacuum field, and the only terms included in the optimization were $f_L$
. This configuration is relatively far to the right on the band of four-field-period QH data in figure 3. It is a vacuum field, and the only terms included in the optimization were $f_L$![]() , $f_{\boldsymbol {\nabla } }$
, $f_{\boldsymbol {\nabla } }$![]() , $f_{\boldsymbol {\nabla } \boldsymbol {\nabla } }$
, $f_{\boldsymbol {\nabla } \boldsymbol {\nabla } }$![]() and $f_{B2}$
and $f_{B2}$![]() . The rotational transform is $\iota = 1.78$
. The rotational transform is $\iota = 1.78$![]() . The plasma shape is shown in figure 11 for $a=0.13$
. The plasma shape is shown in figure 11 for $a=0.13$![]() , corresponding to $A=5.8$
, corresponding to $A=5.8$![]() . The axis shape of this configuration resembles the one in figure 2 of Rodriguez et al. (Reference Rodriguez, Sengupta and Bhattacharjee2022b). Given the boundary computed by the near-axis equations, the field strength inside is computed with DESC and displayed in figure 12, showing excellent QH symmetry. This configuration has a magnetic hill.
. The axis shape of this configuration resembles the one in figure 2 of Rodriguez et al. (Reference Rodriguez, Sengupta and Bhattacharjee2022b). Given the boundary computed by the near-axis equations, the field strength inside is computed with DESC and displayed in figure 12, showing excellent QH symmetry. This configuration has a magnetic hill.

Figure 11. A four-field-period quasi-helically symmetric stellarator generated from the near-axis method, with large ratio of magnetic axis length to major radius (12.0). (a) Cross-sections. (b) The same configuration is shown from three perspectives. Colour indicates the field strength, and black curves are field lines.

Figure 12. Magnetic field strength on the boundaries of the four-field-period quasi-helically symmetric stellarators, computed by running a fully 3-D fixed-boundary equilibrium calculation inside the boundary constructed from the near-axis method. The mostly straight diagonal contours confirm the QH symmetry. The configurations correspond to figures 11 and 13.
Next, we present a vacuum configuration with magnetic well, obtained by including the $f_{\mathrm {well}}$![]() term in the objective. This configuration has a magnetic axis length $L/R_0=7.0$
term in the objective. This configuration has a magnetic axis length $L/R_0=7.0$![]() , shorter than the previous configuration. The rotational transform is $\iota = 1.18$
, shorter than the previous configuration. The rotational transform is $\iota = 1.18$![]() . The plasma shape is shown in figure 13 for $a=0.13 R_0$
. The plasma shape is shown in figure 13 for $a=0.13 R_0$![]() , corresponding this time to $A=7.1$
, corresponding this time to $A=7.1$![]() . This plasma shape is fairly similar to previous four-field-period QHs (Anderson et al. Reference Anderson, Almagri, Anderson, Matthews, Talmadge and Shohet1995; Ku & Boozer Reference Ku and Boozer2011; Bader et al. Reference Bader, Faber, Schmitt, Anderson, Drevlak, Duff, Frerichs, Hegna, Kruger and Landreman2020; Landreman & Paul Reference Landreman and Paul2022). The field strength inside this boundary computed by DESC is shown in figure 12. A QH pattern is apparent, although the deviations from QH symmetry are larger than in the previous configuration, even though $a$
. This plasma shape is fairly similar to previous four-field-period QHs (Anderson et al. Reference Anderson, Almagri, Anderson, Matthews, Talmadge and Shohet1995; Ku & Boozer Reference Ku and Boozer2011; Bader et al. Reference Bader, Faber, Schmitt, Anderson, Drevlak, Duff, Frerichs, Hegna, Kruger and Landreman2020; Landreman & Paul Reference Landreman and Paul2022). The field strength inside this boundary computed by DESC is shown in figure 12. A QH pattern is apparent, although the deviations from QH symmetry are larger than in the previous configuration, even though $a$![]() is identical and $A$
is identical and $A$![]() is larger. This finding, that there is a significant trade-off between quasisymmetry and magnetic well, was also observed in Landreman & Paul (Reference Landreman and Paul2022). The quality of quasisymmetry can be improved to any desired degree by increasing the aspect ratio. This is shown in the right panel of figure 12, displaying the field strength from DESC when the plasma boundary is constructed for a value of $r$
is larger. This finding, that there is a significant trade-off between quasisymmetry and magnetic well, was also observed in Landreman & Paul (Reference Landreman and Paul2022). The quality of quasisymmetry can be improved to any desired degree by increasing the aspect ratio. This is shown in the right panel of figure 12, displaying the field strength from DESC when the plasma boundary is constructed for a value of $r$![]() that is half as large, giving $A=14$
that is half as large, giving $A=14$![]() . For this higher aspect ratio the $B$
. For this higher aspect ratio the $B$![]() contours are significantly straighter.
contours are significantly straighter.

Figure 13. A four-field-period quasi-helically symmetric stellarator generated from the near-axis method, with magnetic well. (a) Cross-sections. (b) The same configuration is shown from three perspectives. Colour indicates the field strength, and black curves are field lines.
Finally, a four-field-period configuration with finite $\beta$![]() and Mercier stability is presented in figure 14. For this configuration, a finite pressure gradient is included by setting ${p_2=-10^6}$
and Mercier stability is presented in figure 14. For this configuration, a finite pressure gradient is included by setting ${p_2=-10^6}$![]() Pa m$^{-2}$
Pa m$^{-2}$![]() , and the $f_{\mathrm {Merc}}$
, and the $f_{\mathrm {Merc}}$![]() term is included in the objective. The rotational transform of the configuration is $\iota =1.60$
term is included in the objective. The rotational transform of the configuration is $\iota =1.60$![]() . Based on experience so far, including $f_{\mathrm {Merc}}$
. Based on experience so far, including $f_{\mathrm {Merc}}$![]() in the optimization causes a substantial deterioration in the minimum aspect ratio, $R_0 / r_c$
in the optimization causes a substantial deterioration in the minimum aspect ratio, $R_0 / r_c$![]() . For this reason, a small minor radius is chosen for the plots, $a = 0.06 R_0$
. For this reason, a small minor radius is chosen for the plots, $a = 0.06 R_0$![]() . Almost all optimized stellarators have a ‘bean-shaped’ cross-section, but figure 14 shows that this configuration does not. Instead, at the toroidal angle for which the major radius of the magnetic axis is maximized, this configuration has reversed triangularity. This configuration also is unique in that it exhibits much stronger magnetic shear (computed from the fully 3-D solution) than the other configurations in this paper. We have observed similar solutions with Mercier stability also for $n_{\mathrm {fp}}=3$
. Almost all optimized stellarators have a ‘bean-shaped’ cross-section, but figure 14 shows that this configuration does not. Instead, at the toroidal angle for which the major radius of the magnetic axis is maximized, this configuration has reversed triangularity. This configuration also is unique in that it exhibits much stronger magnetic shear (computed from the fully 3-D solution) than the other configurations in this paper. We have observed similar solutions with Mercier stability also for $n_{\mathrm {fp}}=3$![]() . The field strength on the finite-aspect-ratio boundary computed by DESC is shown in figure 15, displaying the expected quasisymmetry. In the future it would be valuable to further explore this unusual class of QH configurations that lack a bean-shaped cross-section. Other important questions for future work are whether Mercier stability can be obtained with larger values of the minor radius $r_c$
. The field strength on the finite-aspect-ratio boundary computed by DESC is shown in figure 15, displaying the expected quasisymmetry. In the future it would be valuable to further explore this unusual class of QH configurations that lack a bean-shaped cross-section. Other important questions for future work are whether Mercier stability can be obtained with larger values of the minor radius $r_c$![]() , and whether Mercier stability is in fact necessary or not in experiments.
, and whether Mercier stability is in fact necessary or not in experiments.

Figure 14. A four-field-period quasi-helically symmetric stellarator generated from the near-axis method, with Mercier stability. This configuration is unique in having a reversed-triangularity cross-section in place of the usual bean-shaped cross-section. (a) Cross-sections. (b) The same configuration is shown from three perspectives. Colour indicates the field strength, and black curves are field lines.

Figure 15. Magnetic field strength on the boundary of the four-field-period quasi-helically symmetric stellarator with Mercier stability, computed by running a fully 3-D fixed-boundary equilibrium calculation inside the boundary constructed from the near-axis method. The straight diagonal contours confirm the QH symmetry.
5.5. Quasi-helical symmetry with seven field periods
To our knowledge, in previously reported QH configurations, the highest number of field periods has been six (Nührenberg & Zille Reference Nührenberg and Zille1988). With the near-axis method, as already mentioned, QH solutions were found also for larger numbers of field periods, passing the filters also for $n_{\mathrm {fp}}=7$![]() and 8. A seven-field-period configuration is shown in figure 16, for $a / R_0 = 0.15$
and 8. A seven-field-period configuration is shown in figure 16, for $a / R_0 = 0.15$![]() . This configuration is a vacuum field with very large rotational transform, $\iota \approx 3.65$
. This configuration is a vacuum field with very large rotational transform, $\iota \approx 3.65$![]() . A target axis length $L_* / R_0 = 14$
. A target axis length $L_* / R_0 = 14$![]() was used. As with the $n_{\mathrm {fp}}=2$
was used. As with the $n_{\mathrm {fp}}=2$![]() QH configuration, it takes a large number of Fourier modes to represent this configuration in cylindrical coordinates. This can be understood from the unusual shaping, with sections of the plasma column that are nearly vertical.
QH configuration, it takes a large number of Fourier modes to represent this configuration in cylindrical coordinates. This can be understood from the unusual shaping, with sections of the plasma column that are nearly vertical.

Figure 16. A seven-field-period quasi-helically symmetric stellarator generated from the near-axis method. (a) Cross-sections. (b) The same configuration is shown from three perspectives. Colour indicates the field strength, and black curves are field lines.
Figure 17 shows the field strength computed with DESC for the surface with ${a/R_0=0.05}$![]() . The straight $B$
. The straight $B$![]() contours in the figure confirm the good QH symmetry.
contours in the figure confirm the good QH symmetry.

Figure 17. Magnetic field strength on the $a/R_0=0.05$![]() surface of the seven-field-period quasi-helically symmetric stellarator, computed by running a fully 3-D fixed-boundary equilibrium calculation inside the boundary constructed from the near-axis method. The straight diagonal contours confirm the QH symmetry.
surface of the seven-field-period quasi-helically symmetric stellarator, computed by running a fully 3-D fixed-boundary equilibrium calculation inside the boundary constructed from the near-axis method. The straight diagonal contours confirm the QH symmetry.
6. Discussion and conclusions
In this work we have demonstrated a method to rapidly compute approximately quasisymmetric stellarator equilibria, and to map out the space of quasisymmetric configurations. The approach is based on expanding the relevant equations about the magnetic axis, and applying optimization to the reduced equations. Optimization is not required to obtain quasisymmetry when using this expansion, since it can be imposed directly (to $O(r)$![]() ) in a neighbourhood of the axis. However, it is useful to apply optimization in practice to the axis shape and other near-axis parameters, to increase the range of minor radius over which the expansion is accurate. Optimization can also be used to achieve other potentially desirable properties such as magnetic well or a desired rotational transform. A large number of diagnostic quantities can be computed directly within the near-axis expansion and included in the objective function. Due to the reduction of the equations by the expansion, a complete optimization takes only of the order of a cpu second. Therefore it is feasible to carry out wide scans over parameter space.
) in a neighbourhood of the axis. However, it is useful to apply optimization in practice to the axis shape and other near-axis parameters, to increase the range of minor radius over which the expansion is accurate. Optimization can also be used to achieve other potentially desirable properties such as magnetic well or a desired rotational transform. A large number of diagnostic quantities can be computed directly within the near-axis expansion and included in the objective function. Due to the reduction of the equations by the expansion, a complete optimization takes only of the order of a cpu second. Therefore it is feasible to carry out wide scans over parameter space.
From the parameter scans shown in figure 3, several previous observations about quasisymmetric stellarators are reproduced, and some new observations can be made. The QA solutions are best obtained at $n_{\mathrm {fp}}=2$![]() , with some marginal solutions also for $n_{\mathrm {fp}}=3$
, with some marginal solutions also for $n_{\mathrm {fp}}=3$![]() , and are limited to $\iota <1$
, and are limited to $\iota <1$![]() . The QH solutions have $\iota > 0.9$
. The QH solutions have $\iota > 0.9$![]() . As recently observed by Rodriguez et al. (Reference Rodriguez, Sengupta and Bhattacharjee2022b), QH and QA solutions exist in continuous bands along which the axis length varies. Along the QA bands, $\iota$
. As recently observed by Rodriguez et al. (Reference Rodriguez, Sengupta and Bhattacharjee2022b), QH and QA solutions exist in continuous bands along which the axis length varies. Along the QA bands, $\iota$![]() varies significantly, whereas $\iota$
varies significantly, whereas $\iota$![]() varies more weakly along the QH bands. QH solutions also exist with many possible values of $n_{\mathrm {fp}}$
varies more weakly along the QH bands. QH solutions also exist with many possible values of $n_{\mathrm {fp}}$![]() , including as few as two.
, including as few as two.
In the remainder of this section, we list some of the many directions for future work. First, more could be done to explore patterns in the database of configurations from § 4. Using other configuration properties besides $\iota$![]() and axis length, the data may be separable into clusters differently, such as configurations with vs without a bean cross-section (e.g. figure 14). It would also be valuable to try to understand patterns in the data, such as the fact that QA solutions seem limited to $n_{\mathrm {fp}}=2$
and axis length, the data may be separable into clusters differently, such as configurations with vs without a bean cross-section (e.g. figure 14). It would also be valuable to try to understand patterns in the data, such as the fact that QA solutions seem limited to $n_{\mathrm {fp}}=2$![]() and 3, by applying analytic methods to the underlying Garren–Boozer equations. Structures in the space of configurations were recently explored using a different method in Rodriguez et al. (Reference Rodriguez, Sengupta and Bhattacharjee2022b), and hopefully connections could be drawn between that work and the methods here.
and 3, by applying analytic methods to the underlying Garren–Boozer equations. Structures in the space of configurations were recently explored using a different method in Rodriguez et al. (Reference Rodriguez, Sengupta and Bhattacharjee2022b), and hopefully connections could be drawn between that work and the methods here.
Some of the QH solutions here, such as those in figures 6 and 16, may not have been seen previously since they require many Fourier modes to represent using the usual boundary shape representation in cylindrical coordinates. It may therefore be valuable to develop near-axis and 3-D MHD equilibrium codes that can use other coordinate systems, such as is being pursued with the code GVEC (Maurer et al. Reference Maurer, Navarro, Dannert, Restelli, Hindenlang, Görler, Told, Jarema, Merlo and Jenko2020). It would also be advantageous to modify the workflow used here so the surfaces are constructed using a poloidal angle other than the Boozer $\theta$![]() , an angle in which the Fourier spectrum of the surface is more compressed.
, an angle in which the Fourier spectrum of the surface is more compressed.
We also find in the scans that there is a significant trade-off between the accuracy of quasisymmetry versus magnetic well (relevant for low $\beta$![]() ) or Mercier stability (relevant at finite $\beta$
) or Mercier stability (relevant at finite $\beta$![]() ). This finding motivates further work on nonlinear MHD stability, to assess whether these measures of linear stability are in fact necessary constraints to impose on a design, or whether they can be relaxed.
). This finding motivates further work on nonlinear MHD stability, to assess whether these measures of linear stability are in fact necessary constraints to impose on a design, or whether they can be relaxed.
Compared with the unconstrained local optimizations used in this work, other optimization methods could be applied to the near-axis model in the future. Algorithms for optimization with constraints could be used instead of the unconstrained approach with penalty terms used here. Also, global algorithms could be applied, since there is no guarantee that the scans here have found all global optima.
There are many other directions for future work. One important question is how to include the bootstrap current in the near-axis model, given the limited freedom in the current profile shape at $O(r^2)$![]() . Second, the methods here could be further developed for QI configurations, building on the work in Plunk et al. (Reference Plunk, Landreman and Helander2019), Jorge et al. (Reference Jorge, Plunk, Drevlak, Landreman, Lobsien, Mata and Helander2022) and Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022). Finally, there is potential for using the geometry relevant to the gyrokinetic equation and ballooning stability, computed from the near-axis quantities by Jorge & Landreman (Reference Jorge and Landreman2021). Properties of gyrokinetic or ballooning modes could potentially be targeted in the optimizations.
. Second, the methods here could be further developed for QI configurations, building on the work in Plunk et al. (Reference Plunk, Landreman and Helander2019), Jorge et al. (Reference Jorge, Plunk, Drevlak, Landreman, Lobsien, Mata and Helander2022) and Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022). Finally, there is potential for using the geometry relevant to the gyrokinetic equation and ballooning stability, computed from the near-axis quantities by Jorge & Landreman (Reference Jorge and Landreman2021). Properties of gyrokinetic or ballooning modes could potentially be targeted in the optimizations.
Acknowledgements
Conversations about the near-axis expansion with R. Jorge and E. Rodriguez are gratefully acknowledged. Assistance with the DESC code was provided by D. Dudt, R. Conlin and D. Panici.
Editor Per Helander thanks the referees for their advice in evaluating this article.
Declaration of interest
The authors report no conflict of interest.
Funding
This work was supported by the U.S. Department of Energy, Office of Science, Office of Fusion Energy Science, under award number DE-FG02-93ER54197.
Data availability statement
The data that support the findings of this study are openly available in Zenodo at https://doi.org/10.5281/zenodo.7108893.